基于子模型技术的车体结构可靠性优化设计

2022-11-21陈志豪宫琦李永华

机械工程师 2022年11期

陈志豪，宫琦，李永华

（大连交通大学机车车辆工程学院，辽宁大连 116028）

0 引言

车体作为轨道交通车辆的核心承载结构，在高速行驶状态下面临着保证车体强度满足安全运行要求的挑战，复杂的运行环境容易导致其薄弱位置产生应力集中，进而对其运行品质产生影响，为此研究车体结构的可靠性并展开优化设计具有重要意义。

研究人员对于车体的结构优化开展了技术攻关并取得了一定成果：石晓飞等[1]为了提升车体的一阶垂弯频率，基于相对灵敏度分析结果，选择对模态频率变化影响显著的设计变量进行尺寸优化，提升了车体的刚度性能；王东等[2]以实现车体轻量化为目标，在对车体静强度分析后，确定容易产生应力集中的位置并调整相应结构，成功完成车体减重；段华东等[3]利用APDL语言编写车体结构优化命令流，对车体参数化模型优化求解和结果寻优，优化后车体质量明显降低；郑若瑜等[4]建立车体优化数学模型，基于OptiStruct软件进行尺寸优化，考虑实际受力特征对得到的优化方案对比验证，降低了局部应力集中现象；王超等[5]采用Lanczos法分析车体模态振型，考虑引起车体抖动的因素，通过优化结构布局，使车体模态频率达到要求。以上人员对车体的优化方案需要重复调整结构，仿真工作量大，对车体部分重点位置的强度校核比较困难，计算效率较低。

为了高效地实现车体强度校核、减轻车质量、提升车体结构可靠性。本文将子模型技术与响应面方法相结合，并采用NSGA-Ⅱ算法求解车体可靠性优化模型，提升了车体的结构可靠性，保证了结果的精确性，技术流程如图1所示。

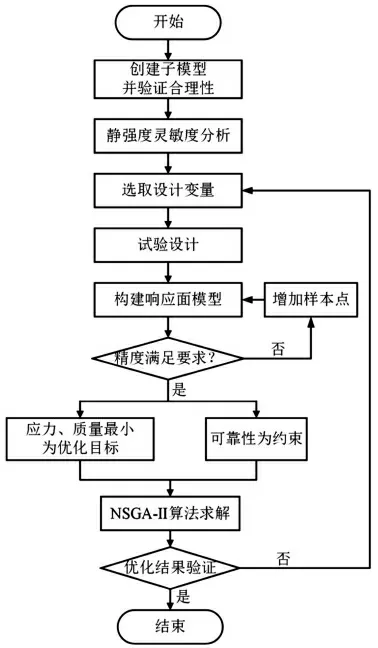
图1 车体结构可靠性优化流程图

1 子模型技术原理

子模型技术基于圣维南原理，该技术从整体模型中选取关注区域划分更加精细的网格[6-7]，对局部结构进行强度校核，提升了分析结果的精确度。子模型的创建步骤如下：1）首先对整体模型计算分析，计算结束保存整体模型的.db和.rst文件；2）对整体模型的关键结构或应力集中区域分割创建子模型；3）将子模型切割边界节点写入Node文件，根据节点坐标计算切割边界上的位移和体载荷并进行插值计算；4）编辑子模型命令流语言，调用整体模型结果文件，施加对应位置的载荷在子模型上，读取切割边界插值文件，完成子模型计算分析；5）对比子模型与整体模型切割边界应力值，验证切割边界选择的正确性，应力值大小一致则可进行后续分析，否则重新选取。

2 可靠性优化理论

2.1 可靠性优化

可靠性优化是在传统确定性优化的基础上，考虑设计变量的不确定性，以可靠度作为约束条件进行优化，提升产品结构性能的方法。多目标可靠性优化指可靠性优化过程中，满足一定的可靠度约束，实现两个及以上的优化目标，但各子目标实际之间存在相互冲突，并不能确保每个优化目标都取得最优解。为了平衡目标函数间的矛盾，最大程度达到全局最优，选取其中一组最优解以达到子目标间的妥协，这组解集称为pareto最优解[8]。多目标可靠性优化数学模型如下：

式中：f（x）为优化目标；gj（x）为第j个确定约束；rj为可靠度的目标值；xL、xU分别代表变量x的上、下限。

2.2 响应面法

响应面法（RSM）是一种将试验设计与数理统计相结合的方法[9-10]，利用试验设计得到设计变量和响应值之间的关系方程。工程中常用的二次多项式响应面方程表达式如下：

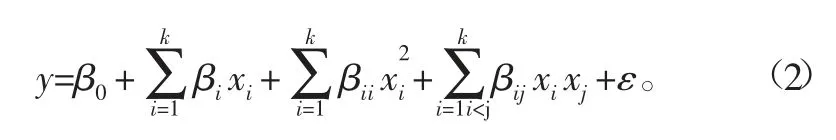
式中：β为常数项；x为设计变量；k为设计变量个数；ε为拟合误差。

精确的响应面模型能够表明输入、输出变量之间的响应关系，因此试验设计方法的选择十分关键，使用较多的试验设计方法主要有D-最优设计、均匀设计、正交试验、拉丁方试验。

3 车体多目标可靠性优化

3.1 建立车体结构子模型

由于车体结构复杂，体积庞大，划分网格工作量大，因此针对车体的结构特点对几何模型适当简化，采用Hypermesh软件划分车体网格，车体有限元模型主要由Shell181壳单元构成，为了确保仿真结果的准确度，Shell单元应减少三角形单元的使用，选择四边形单元，利用Beam188梁单元和RBE3刚性单元模拟车体设备与车体的连接及点焊关系。车体有限元模型单元总数为1 921 278个，节点总数为1 407 337个，整车有限元模型如图2所示。根据EN 12663-1：2010《铁道应用-铁路车辆车体的结构要求》等标准对车体施加静强度载荷和约束，并选择其中5种典型工况计算分析，具体结果如表1所示。

图2 车体有限元模型

由表1可知，各工况下的最大应力均符合材料的强度要求。但在AW0纵向拉伸工况中车体顶棚产生较大应力集中，为了判断顶棚结构的可靠性对其建立子模型深入分析，并依据分析结果进行优化设计。子模型应力云图如图3所示。

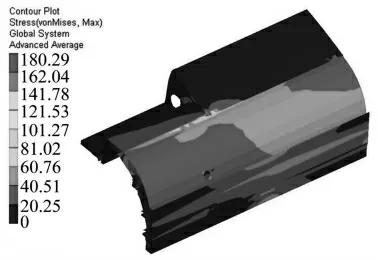
图3 子模型应力云图

表1 主要计算工况及结果

在子模型创建过程中，切割边界的选择应远离应力集中区域[11-12]。本文选取的切割边界B1～B4如图4所示，切割边界部分节点坐标如表2所示，部分节点位移如表3所示。

表2 子模型切割边界部分节点坐标

表3 子模型切割边界节点位移

图4 子模型切割边界

正确的切割边界才能保证计算结果的准确性，对切割边界应力值大小进行比较，判断选择的边界是否正确，本文选取B1切割边界为例，对比结果如图5所示。

由图5可知，切割边界对比应力值相差范围较小，表明选择的切割边界较为合理，可进行后续的仿真分析。

图5 切割边界应力对比图

3.2 子模型可靠性分析

灵敏度分析是判断设计变量的变化对输出结果的影响程度[13]，对于具有一个设计变量的函数F（x），对函数F（x）求导即为变量的灵敏度；当函数F（x）含有多个设计变量时，F（x）的偏导数即为灵敏度，用数学公式表示为

式中：S1为一阶差分灵敏度；S2为一阶微分灵敏度。通过灵敏度分析降低了优化函数的复杂性，从而提升了优化效率。

本文将子模型最大应力值作为输出响应，板厚作为输入变量，各设计变量参数如表4所示，通过在ANSYS -PDS 模块中计算得到子模型灵敏度分析结果如图6所示，图6灵敏度为正，表明应力随着板厚的增大而变大；灵敏度为负，则应力随着板厚的增大而减小。

表4 设计变量参数

由图6可以看出，T2、T3、T4、T5、T7对子模型的等效应力值影响较大。因此选择上述5个板厚作为设计变量进行试验设计，各变量的初始值和取值范围如表5所示。

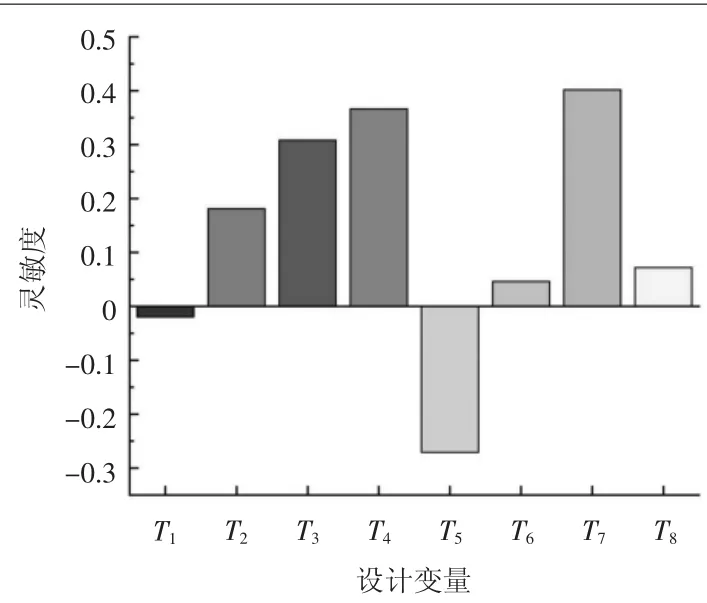
图6 灵敏度结果

利用CCD对表5中的随机变量进行试验设计，得到46组试验数据，试验数据如表6所示。

表5 设计变量取值范围

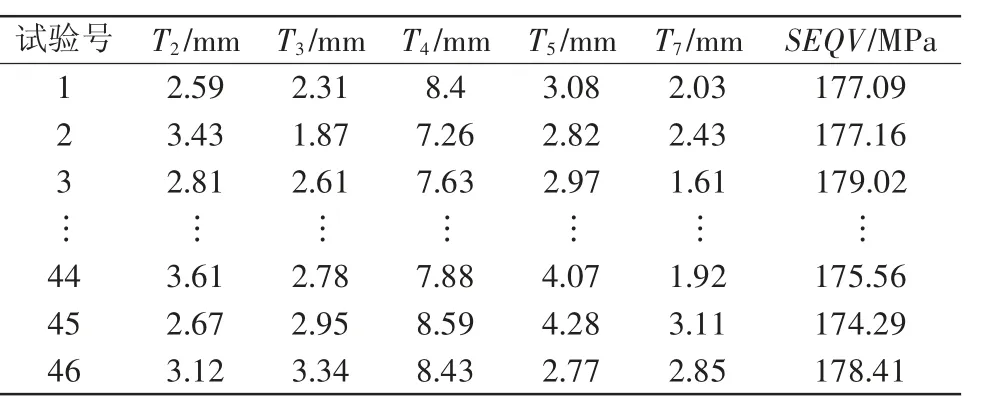
表6 试验设计值

为了直观显示设计变量对子模型最大应力的影响，任意选择两个设计变量代表X轴和Y轴，Z轴代表子模型最大应力，使用Matlab软件绘制样本空间，如图7所示。

由图7 可知，样本空间中试验设计点分布较为均匀，表明试验设计较为合理，且不存在样本点重复现象，确保了试验结果的精确性。将试验设计所得样本点进行响应面拟合，结果如图8所示。

图7 设计变量T2-T3样本空间分布

由图8 可知，随着T2、T3、T4、T7的增大，应力值有所增大，且变量T7对应力大小的变化程度影响显著，与灵敏度分析结果吻合。利用最小二乘法对样本点拟合，得到子模型最大应力S和质量M的多项式响应面函数为：

图8 响应面模型

通过比较试验样本点残值范围来判断响应面拟合精度，响应面复相关系数R2为0.98，说明拟合程度较好，试验样本残差图如图9所示。

由图9 可知，最大应力实际值和预测值大小相近，残差值最大为0.6，样本点整体残差值均较小，说明响应面函数满足精度要求，拟合效果好，能进行后续仿真分析。

图9 试验样本残差图

将子模型文件导入ANSYS，选择Monte Carlo法进行可靠性分析，考虑子模型结构尺寸、材料属性的随机性，将结构尺寸作为输入变量，子模型最大应力及极限状态方程值为输出变量，在ANSYS中经过500 次循环后，得到子模型最大应力抽样历史、极限状态函数值趋势图如图10、图11所示。

由图10可知，经过500 次抽样后，子模型最大应力抽样历史集中在212.5～215.0 MPa之间，接近材料的屈服极限，应力值存在超过材料的屈服强度的情况；由图11可知，该曲线横坐标表示结构最大应力值，纵坐标表示该点对应的结构最大应力值在整个抽样结果中小于该值的概率，由此可知子模型静强度可靠度为83.3%，仍有提升的空间。

图10 最大应力抽样历史

图11 极限状态函数值趋势图

3.3 优化求解

根据灵敏度分析结果选取板厚T2、T3、T4、T5、T7作为设计变量，以板厚变化范围和可靠度大于83.3%为约束条件，子模型等效应力和质量最小值为优化目标建立多目标可靠性优化数学模型，其数学表达式为：

采用非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm，NSGA-II）对数学模型优化求解，NSGA-II算法由NSGA算法改进而来，具有精度高、速度快的优点，能快速对解的优劣进行评估，保证非劣解集的多样性和空间分布均匀性[14]，求解得到Pareto 解集，如图12所示。

由图12可知，质量与应力的变化形势相互矛盾，应力降低，质量则随之增大。为了达到两个子目标间的平衡，考虑工程实际等因素，选择其中一组解作为pareto最优解，对应的子模型质量为40.5 kg，最大应力为166 MPa，优化前后子模型参数对比如表7所示。