城市轨道交通停车线设置对故障救援影响的定量分析*
2022-11-21王晓潮刘致远杨子涵
彭 磊 王晓潮 刘致远 杨子涵
(1.广州地铁设计研究院股份有限公司,510010,广州;2.天津市英贝特航天科技有限公司,300141,天津;3.北京交通大学交通运输部综合交通运输大数据应用技术交通运输行业重点实验室,100044,北京∥第一作者,高级工程师)
随着城市轨道交通的发展,城市轨道交通列车的准时性和安全性成为乘客和运营商共同关注的问题。然而,列车故障时有发生。该如何选择快速、高效、安全的故障救援方案,使故障列车尽快退出运营正线,使故障影响最小化,是众多研究关注的热点课题。
既有研究的关注点大多集中在停车线设置方案,即在工程投资与故障救援影响两者之间进行权衡,并根据工程案例对不同停车线配置方案进行对比分析[1-4]、建立布局模型[5]等。综上,既有研究多采用定性分析的方法,且缺乏对全线路各个位置发生故障可能性的全面考量。
本文针对以往研究中缺乏对停车线设置方案定量分析的情况,拟通过总结列车故障救援方案种类、构建列车故障救援模型和全线救援延误计算模型的方法,进行城市轨道交通列车停车线设置方案对故障救援影响的定量分析,并将本文提出的定量分析方法在工程案例中进行测试验证。
1 城市轨道交通列车故障救援方案分析
通过对国内外救援案例的总结进行分析[6-8],发现城市轨道交通列车(以下简为“城轨列车”)故障救援方案有3个核心要素:救援列车、救援方向和故障列车存放地点。这3个要素的不同组合形成了不同的城轨列车故障救援方案。
在救援列车的选择上共有后序列车、前序列车和对向列车3种方式可以考虑。运营中的城轨列车发生故障后,一般会将后序列车在后方车站扣停,在进行救援时由后序列车进行清客救援最节省时间。因此,国内城轨列车在现场多选用后序列车作为救援列车。然而,采用前序列车或对向列车进行正向救援时为牵引连挂方式,相较于后序列车推送故障列车救援,救援速度更快,在长距离救援情况下更具有优势。
在救援方向的选择上,现场多以正向救援为主,在城轨列车发生故障后距离后方停车线较近,或刚出两端折返站时会考虑反向救援。然而,反向救援时会与后序列车产生冲突,救援距离有限。在此基础上,额外考虑对向救援,其救援方向与反向救援一致,但将故障列车通过渡线转移到对向线路,虽然增加了对对向线路的影响,但大大延长了反向救援距离。需要说明的是当前序列车或对向列车作为救援列车时仅考虑正向救援。这是由于对于前序列车或对向列车只有进行正向救援,用牵引代替推送才能降低延误,进行反向或对向救援反而会增加延误[9]。
对于故障列车存放地点的选择,本文只考虑城轨列车停车线及车辆段。其中,对于停车线,按照其类型和与线路相对位置将其划分为:贯通式单列位停车线、贯通式双列位停车线、尽头式单列位停车线和尽头式双列位停车线。
基于上述分析,本文对多种救援方案按照救援路径的不同进行了精简分类,将城轨列车故障救援方案归纳为5种类型:后序列车正向救援,后序列车反向救援,后续列车对向救援,前序列车正向救援及对向列车正向救援;并与不同的故障列车存放点组合形成多种不同的列车故障救援方案,如图1所示。其中后序列车对向救援和对向列车正向救援会影响对向线路运营,对运营组织的要求较高,实际运营中可以按实际需要进行选择。
2 停车线对故障列车救援影响定量分析
2.1 城市轨道交通列车故障救援模型
为进行定量分析,需要构建每种救援方案的救援模型,计算延误时间。延误时间分为一次延误和二次延误2个部分。延误计算用到的参数如表1所示。
分别对后序列车正向救援、后序列车反向救援、后续列车对向救援、前序列车正向救援以及对向列车正向救援的流程进行分析,得到5种救援方案的一次延误计算公式。
1) 后序列车正向救援方案:
2) 后序列车反向救援方案:
T1,12=t判断+t清客+l故后/v接近+
t连挂+l故停/v牵引+t清客
(2)
3) 后序列车对向救援方案:
4)前序列车正向救援方案:
5) 对向列车正向救援方案:
对于双列位停车线和车辆段,可以同时容纳救援列车和故障列车停放,不存在二次延误。因此这3种类型的停放点二次延误均为0,如式(6)所示。
T2,k=0,k=1,2,3
(6)
通过对推送救援和牵引救援的流程分析得到单列位停车线的二次延误计算公式为:
当救援列车推送故障列车进入时,
T2,4=t摘钩换端+t返回+t换端
(7)
当救援列车牵引故障列车进入时,
T2,4=t摘钩+t进入
(8)
但是对于尽头式单列位停车线禁止救援列车牵引故障列车进入,因为救援列车无法回到正线。
至此,对于任意一个救援方案j,设其救援方案路径选择类型为lj,停放位置类型为kj,则其延误时间dj计算为:
dj=T1,lj+T2,kj
(9)
本文利用Opentrack仿真软件对上述计算模型进行了检验。其仿真与计算结果对比如表2所示。检验结果表明,该救援延误时间计算模型具有较高计算精度。

表2 仿真与计算结果对比Tab.2 Comparison of simulation and calculation results
2.2 全线救援延误时间计算模型
为探究停车线设置对于全线故障救援的影响,本研究采用将线路离散化的方法来计算线路整体的救援延误时间,分别计算列车在线路上各个区段发生故障时的救援延误时间。
具体而言就是将上下行线路分别按照相等的间隔进行划分,得到线路区段划分集合。由于区段长度较短,单个区段的故障救援延误时间可由列车在该区段中点发生故障时的最短延误时间表示。之后对所有区段的延误时间进行加权求和获得整体救援延误时间。
考虑到不同区段发生故障的概率不同,可以根据以往故障数据以及客流量大小,对不同区段的延误时间权重进行标定。线路整体救援延误时间的计算公式如下:
(10)
di=min{di,j,j∈J}
(11)
式中:
T——线路整体的救援延误时间;
I——线路划分区段的集合;
J——救援方案的集合;
wi——区段i的延误时间权重;
di,j——区段i在选择救援方案j下的延误。
3 案例分析
本文以福州地铁滨海快线为例,测试本文提出的停车线设置方案定量分析方法。此外在遵守GB 50157—2013《地铁设计规范》中应每隔5~6个车站设置停车线,每隔2~3个车站设置渡线的规定的前提下,本文结合线路情况和定量分析结果,对线路原停车线设置方案进行优化,并对优化前后的停车线设置方案进行对比分析。
福州地铁滨海快线线路(福州站至长乐机场站)总长约为63.30 km,最大站间距为9.96 km,线路配线图如图2所示,各站原停车线设置方案如表3所示。车辆段和停车场在救援过程中不会产生二次延误,因此视为双列位停车线处理。
为得到在原停车线设置方案下该线路的整体救援延误时间,需要对整条线路进行离散化处理,在该案例中以240 m为单位划分区段,整条线路共划分为258个区段。之后以每个区段中点位置发生列车故障(列车失去动力)所造成的延误时间代表该区段故障列车救援的延误时间。假设每个区段权重都设为1/258,可以计算得到原停车线设置方案下线路整体救援延误时间指标为26.79 min。该指标代表线路整体的平均救援延误时间。
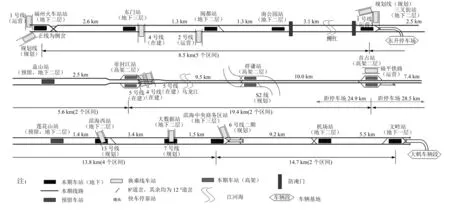
图2 福州地铁滨海快线线路配线图Fig.2 Auxiliary line diagram for Fuzhou-Changle Airport rail transit line
图3展示了福州地铁滨海快线在原停车线设置方案下各区段对应的最短救援延误时间分布情况(横轴上箭头按由高到低依次代表双列位停车线、单列位停车线、渡线、无相关配线)。由图3可以看出上、下行方向均在帝封江站—详谦站,详谦站—首占站,首占站—滨海西站,滨海新城站至机场站这几个长大区间延误较高。这是由于长大区间发生故障时,救援列车需要走行更远的距离才能接近故障列车,这也解释了区间内部为何一般离出发车站越远,延误越大。而从区间的角度看,越接近前方双列停车线的区间延误越小,这是由于双列位停车线没有二次延误,可以显著减少救援延误时间。
本文按照GB 50157—2013 《地铁设计规范》的相关要求,结合福州地铁滨海快线线路情况,通过人工调整设计了新的停车线设置方案。具体而言,为解决原方案在三叉街站至滨海新城站路段救援延误持续较高的现象,新停车线方案采用了在大数据站处设置双列位停车线,在三叉街站至大数据站路段密集布置渡线的方法。新停车线设置方案下各区段对应的最短救援延误时间分布情况如图4所示。该方案将原方案的三个单列位停车线改为了一个双列位停车线并增加了4条渡线,对工程造价的改变不大,但通过与原方案相同的定量分析方法可求得新停车线设置方案的整体救援延误时间指标为23.63 min,较原方案降低了11.80%。
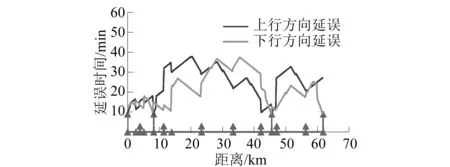
图4 福州地铁滨海快线新停车线设置方案下各区间最短救援延误时间
新停车线方案为在大数据站附近位置故障的列车提供了较近的故障列车停放位置,降低了故障列车救援过程的一次延误时间,而且通过双列位停车线消除了二次延误,从而使大数据站附近区段的平均救援延误降低。在三叉街站至大数据站路段密集布置渡线可以有效地沟通上、下行方向运行的列车,在列车发生故障时可以提供更多救援方案的选择,增加了救援作业的灵活性,从而使双向的救援延误时间更为均衡,在线路整体上体现为救援延误时间的减少。
4 结语
本文总结归纳了列车故障救援方案种类,并通过将线路分段化处理,以各区段救援延误时间的加权平均值衡量停车线设置方案对列车故障救援的影响。基于福州地铁滨海快线的案例分析,证明本文提出的方法不仅可以获得线路整体救援延误情况,同时可以获得全线每个区段救援延误情况,为停车线设计工作提供决策支持。后续研究可以在本文定量分析方法的基础上测试更多的线路案例,分析总结停车线类型和位置对故障列车救援的影响规律。
