改进粒子滤波的水下重力匹配导航仿真与实验

欧阳明达， 杨元喜

(1.信息工程大学 地理空间信息学院，河南 郑州 450052； 2.地理信息工程国家重点实验室，陕西 西安 710054)

水下载体导航由于独立性、自主性和隐蔽性要求，往往选择惯性导航手段，但是，惯性导航系统由于累积误差大，一般不适宜长时间、远距离的水下航行导航。惯性导航与其他导航手段的组合或融合可以部分校正惯性系统产生的位置误差积累[1-3]。依靠光学信号的天文导航或依赖无线电信号的全球导航卫星系统(global navigation satellite system,GNSS)导航是开旷地区最常用的定位方式，但是它们只能在本身具备可用性的情况下才能与惯性系统进行组合导航[4]；水声定位导航技术是一种通过测量声波传播的时间、相位、频率等信息实现定位与导航的技术，受复杂海洋环境影响，水声定位导航观测数据受观测有效性低、延迟性高、数据率低、观测受水体环境影响大等特点的制约，水声/惯性组合导航目前尚处于起步阶段，以理论研究为主，实践较少，暂时还未建成海底长期稳定工作的水下大地基准网[5-7]；地磁/惯性组合导航方式由于缺乏地磁基础资料，分辨率较低，且地磁变化较快，离实用化还存在很大差距[8]。

近年来重力匹配导航方式得到国内外学者的广泛关注，先后研制了重力辅助惯性导航系统和重力匹配导航算法[2,9]，经典的算法有地形轮廓匹配(terrain contour matching,TERCOM)算法[10-12]、等值线最近点迭代(iterative closest contour point,ICCP)算法[13-15]、桑迪亚惯性地形辅助导航(sandia intertial terrain contour matching,SITAN)算法[16-17]，这些方法原理相对简单、匹配效率高，早期多用于飞行器地形匹配导航。粒子滤波算法是采用大量随机样本完成贝叶斯滤波的递推过程，通过概率计算，得到位置最优解。与SITAN算法相比，粒子滤波算法无需地形随机线性化过程，更适用于非线性/非高斯的动态系统，但也存在其自身问题，如重要性分布函数难以选取、重要性函数与似然函数不能完好匹配、粒子退化严重等。针对现实应用问题，国内外学者对粒子滤波进行了一系列改进，如：不敏卡尔曼粒子滤波[18-19]、辅助粒子滤波[20]、扩展卡尔曼粒子滤波[21]、高斯和粒子滤波[22]、高斯粒子滤波[23]、Rao-Blackwellized粒子滤波[24]、正则化粒子滤波[25]等，这些改进算法从不同侧面提高了粒子滤波性能。在匹配导航算法实践中，文献[26]提出一种粒子滤波估计方法和轨迹相似变换相结合的二次匹配算法，选择载体位置为滤波模型的状态变量，利用惯导系统短期位移进行滤波模型参数估计，采用粒子滤波方法对载体真实位置进行最优估计；文献[27]针对贝叶斯滤波后验概率密度函数的求解问题，用高斯混合密度函数近似状态的后验概率密度函数，提出了基于高斯和粒子滤波的水下地形匹配导航方法。

本文将粒子滤波算法用于水下重力匹配导航，引入重要性重采样步骤，克服了滤波过程中的粒子退化问题。在详细分析粒子滤波受不同初始偏差、不同蒙特卡罗采样、不同重力异常观测误差影响的基础上，为了控制初始偏差对匹配精度和计算时效的不利影响，引入粒子群优化算法削弱初始配准误差；通过算例分析验证，联合算法有助于进一步提高精度、提升效率、增强可靠性。

1 匹配算法原理

1.1 贝叶斯估计

非线性随机系统可以用系统状态方程表示为：

xk+1=fk(xk,wk)

(1)

系统观测方程为：

zk=hk(xk,vk)

(2)

式中：xk为系统状态向量；zk为k时刻的观测向量；wk为过程噪声；vk为观测噪声。

根据贝叶斯理论，给定后验概率密度函数或后验密度p(xk|z1:k)以及k时刻所有可用观测向量z1:k={z1,z2,…,zk}估计xk出现的概率[28]，这个概率值即为p(xk|z1:k)。状态向量的初始概率为p(x0|z0)，所求概率可以通过预测和更新2步法得到。预测阶段使用公式为：

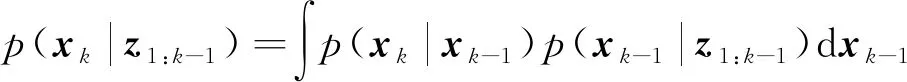
(3)

式中：p(xk|z1:k-1)为前一个后验密度。给定测量值zk，更新阶段通过贝叶斯准则得到后验密度为：

(4)

归一化常数：

(5)

从上述递推过程可知，计算过程涉及大量积分运算，由于观测方程式(2)一般为非线性方程，且观测不一定服从正态分布，所以很难得到后验概率积分值，通常采用蒙特卡罗采样方法。

1.2 序贯重要性采样算法

序贯重要性采样(sequential important sampling,SIS)算法是一种蒙特卡罗(Monte Carlo,MC)方法，通过一组具有相关权重的随机样本表示后验概率密度函数，并根据这些样本和权重计算估计值[29]。当样本数量变得非常大时，SIS滤波值接近最佳贝叶斯估计。

(6)

式中δ为狄拉克函数。

第i个粒子的归一化权重为：

(7)

(8)

序贯贝叶斯估计的思路是，在每次迭代中，利用样本可以构成p(x0:k-1|z1:k-1)的近似值，并以一组新的观测样本得到p(x0:k|z1:k)的近似值。重要性密度表示为：

q(x0:k|z1:k)=q(xk|x0:k-1,z1:k)q(x0:k-1|z1:k-1)

(9)

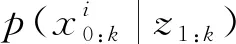
(10)

根据式(9)和式(10)，权重更新方程为：

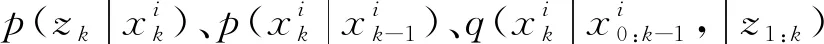
算法1：SIS粒子滤波

fori=1:N

采样粒子：

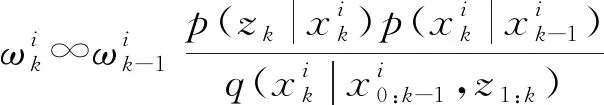
end

1.3 重要性采样(SIR)算法

采用SIS 方法进行递归贝叶斯估计时，会产生严重的粒子退化问题。粒子退化问题是指通过若干次递归计算，除了个别几个粒子具有较大权值外，其余粒子的权值都很小；极端情况下，只有一个粒子具有趋近于 1 的较大权值，所有其他粒子的权值都趋近于0[30-32]。Gordon 等[33]在其提出的自举滤波算法中引入重采样(resampling)步骤，一定程度上解决了粒子退化问题。

重采样的主要思想是，去除那些权值较小的粒子，保留并复制那些权值较大的粒子。重采样的方法有很多，如分层采样、残差采样、系统采样等。一般使用有效粒子Neff来判断粒子权重的退化程度：

2 不同工况条件下的结果讨论

将某海域作为研究对象，重力异常数据采用美国斯克利普斯海洋研究所发布的SIO grav23.1模型，模型为1′分辨率，精度为2 mGal[34]。图1示出了该海域重力异常。给出航迹模拟参数，令真实航迹起始点坐标为22.3°S,105.6°E，航向角45°，载体航行速度10 n mile/h，随机误差均方差为0.06 n mile，指示航迹线性误差在经度方向为0.3 n mile/h，纬度方向为0.5 n mile/h，随机误差均方差为0.12 n mile，航迹点重力异常均方根误差为2 mGal，共有40个采样点。

图1 海域重力异常图

采用粒子滤波算法进行重力匹配导航，设置如下部分固定参数：粒子分布半径6 000 m，粒子数500个，重力观测误差标准差2 mGal。精度误差评价指标采用均方根误差(root mean square error,RMSE)表示为[35]：

本文设定A、B、C 3种不同工况，即不同初始误差、不同蒙特卡罗采样样本量和不同观测误差标准差，分别讨论不同工况的粒子滤波效果。

1)工况A：不同初始偏差

初始偏差是真实航迹相对惯导指示航迹在起始点的偏移量，由于无法提前预知其偏离程度，有必要对不同初始偏差条件下的滤波计算情况进行分析。设定蒙特卡罗采样为10次，初始偏差分别为(1 n mile，0 n mile)、(3 n mile，0 n mile)、(5 n mile，0 n mile)、(9 n mile，0 n mile)，图2示出了不同偏差的粒子滤波计算结果，图3示出了航迹重力异常变化曲线，可以看出：

图2 不同初始偏差的粒子滤波匹配结果

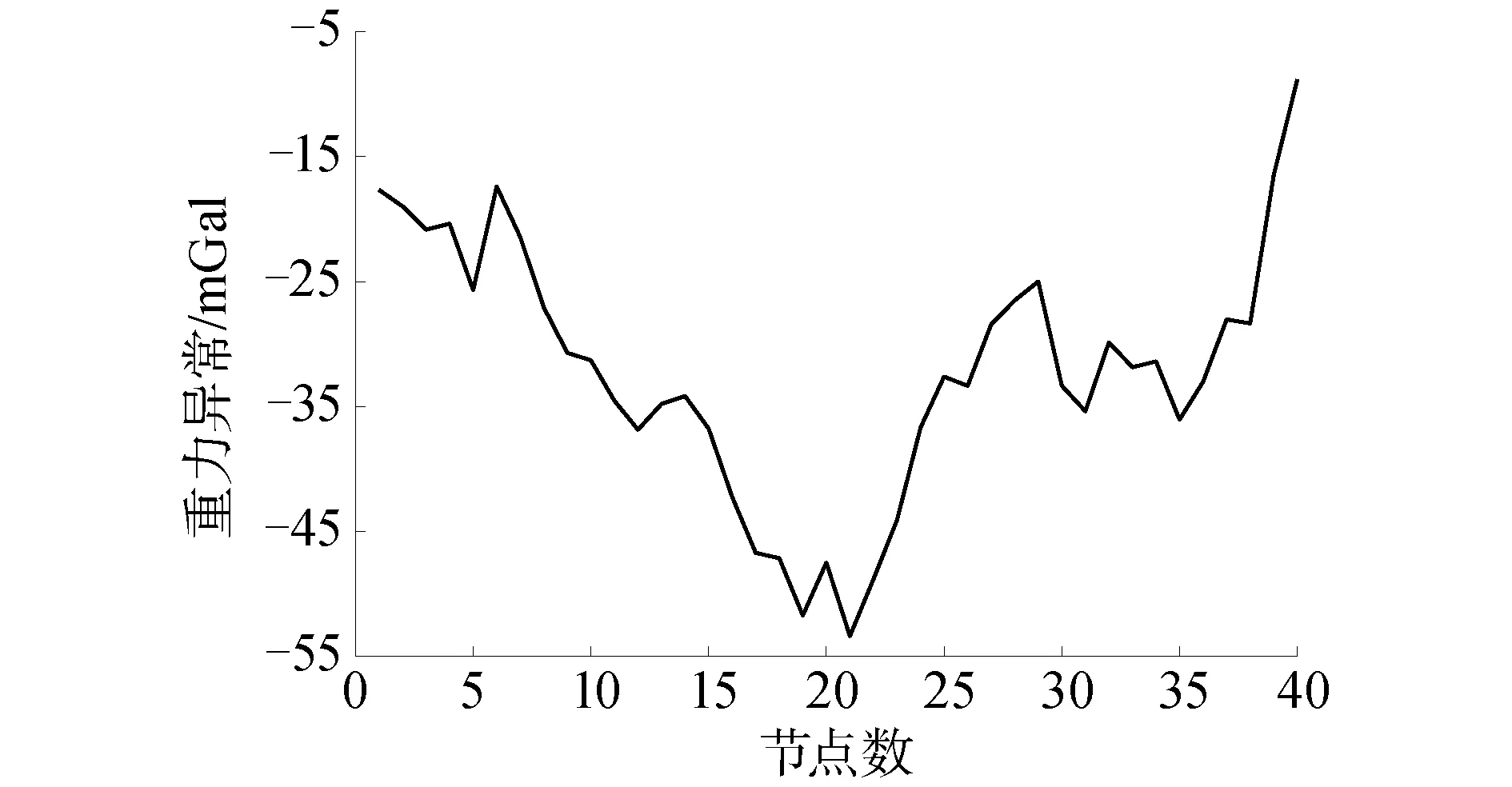
图3 航迹重力异常变化

①航迹点重力异常变化特征明显，适宜开展水下重力匹配导航，相邻点间的重力异常差异较大，航迹点的重力异常观测误差不会淹没相邻2点间的重力异常数据变化；

②匹配航迹能够较好吻合真实航迹，图4示出了航迹的初始段差异值，可以看出，采用粒子滤波算法，初始偏移越大，初始段匹配的位置差异越大，倘若初始偏差超过粒子覆盖范围，很容易造成匹配失败；

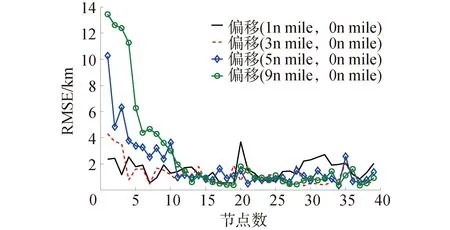
图4 不同初始偏差匹配结果精度

③匹配航迹逐渐向真实航迹靠拢，中后航段匹配精度高于初始航段。由此考虑，当对航迹整体平移后采用滤波计算，即若能通过算法将图2(d)指示航迹平移变换为近似图2(a)指示航迹，所得匹配结果的初始航段精度水平将会有较大改善。

2)工况B：不同次数蒙特卡罗采样

采用多次蒙特卡罗采样，粒子滤波算法在获得高精度匹配结果的同时会牺牲实时性[36]。匹配精度与计算效率之间需要合理平衡，对采用1次、10次、30次、60次蒙特卡罗采样的匹配结果进行分析，图5示出了不同初始偏差的蒙特卡罗采样后匹配结果，可以看出：

图5 不同蒙特卡罗采样匹配结果精度

①当偏差为(1 n mile，0 n mile)，进行1次蒙特卡罗采样后的结果和多次采样后结果未呈现显著差异；当偏差为(9 n mile，0 n mile)时，进行1次蒙特卡罗采样后的结果在初始段精度略低于多次采样后结果；由此可见，初始偏差越小，1次蒙特卡罗采样的稳定性和可靠性更优；

②多次采样后的匹配结果，对精度改善和提升作用不大，甚至有个别点位在多次蒙特卡罗采样后，精度低于较低次数的蒙特卡罗采样结果。计算时效分别为1次，耗时约50 s；10次，耗时约5 min；30次，耗时约14 min；60次，耗时约28 min。进行1次蒙特卡罗采样意味着能够实时性开展水下重力匹配导航，倘若对指示航迹整体平移以缩小初始偏差，则能够得到更高效、更准确、更稳妥的匹配结果。

3)工况C：不同观测误差标准差

设定蒙特卡罗采样次数为10次，对航迹点重力异常分别加入2 mGal、5 mGal、9 mGal、13 mGal、20 mGal的随机误差。图6示出了初始偏差为(1 n mile，0 n mile)和(3 n mile，0 n mile)的不同观测误差下匹配导航结果。图6中，σ′为观测误差标准差。可以看出：

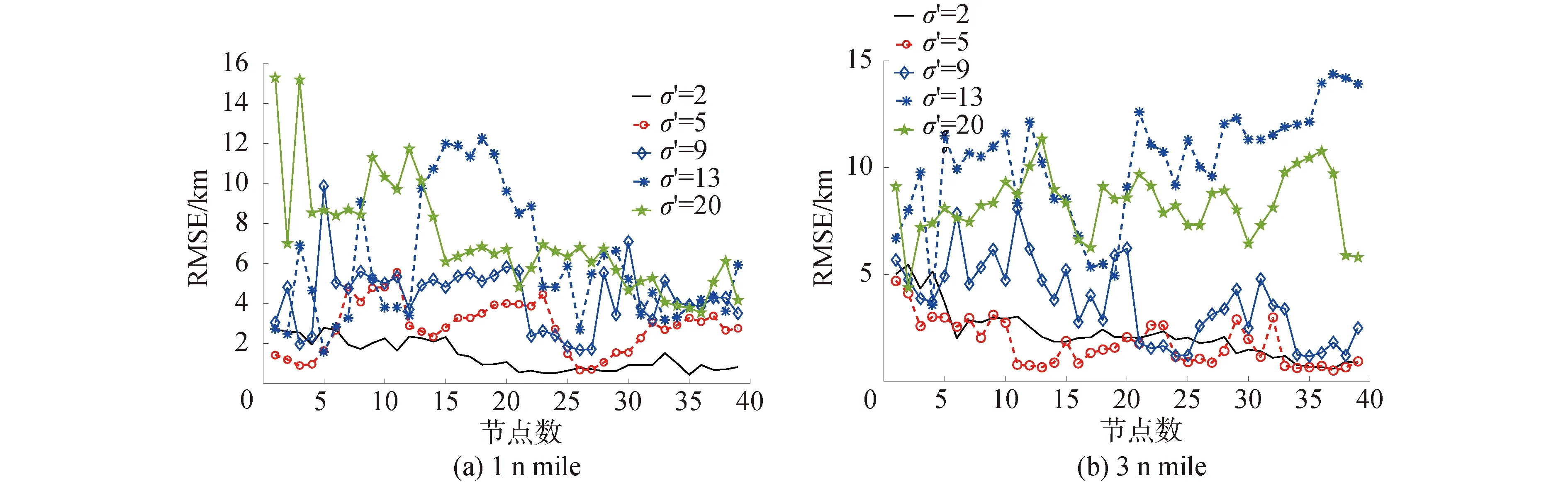
图6 不同观测误差标准差的匹配结果精度

①当初始偏差为(3 n mile，0 n mile)时，匹配导航精度受σ′值变动影响较大，σ′在5 mGal以内时，匹配航迹与真实航迹吻合程度较好，稳定性和精确度较高；当σ′值过大，匹配结果呈现为发散状态，偏离真实航迹越来越远；当初始偏差为(5 n mile，0 n mile)、(9 n mile，0 n mile)时，σ′增大，匹配失败。

②当初始偏差为(1 n mile，0 n mile)时，导航结果精度受σ′值影响程度减弱，当σ′较大时，匹配结果发散程度较偏差较大时的情况有所减缓，整体精度水平更优。由此可见，缩小初始偏差，能够在一定程度上克服实际重力异常观测误差较大带来的负面影响。

3 联合粒子群优化的改进算法

综上，减小初始偏差有助于提升匹配导航定位精度、提高计算效率，有必要对其进行预处理。引入粒子群优化算法，该方法的优点在于不拘泥格网分辨率的限制，通过设定适用性函数引导粒子向最优位置逼近，得到初始段航迹最优匹配解，其与指示航迹起始点间差异即为平移参数。程向红等[37]给出了粒子群优化算法的基本原理。

联合粒子群优化改进算法计算步骤如下：首先，利用粒子群优化算法对初始段航迹进行匹配计算，实现初始点的精确定位；其次，对初始点匹配位置进行标记，得到与惯导指示航迹初始点的位置差异，设置为平移量，将惯导指示航迹整体平移；然后，将平移后航迹作为待匹配航迹，其上的重力异常值保持不变；最后，采用粒子滤波算法，得到匹配航迹，由于初始偏差得到改善，粒子滤波过程采用1次蒙特卡罗采样计算，即可实现实时匹配导航，而后每隔一定航距进行多次蒙特卡罗计算验证结果。

沿用上文算例，设定初始偏移量为(9 n mile，0 n mile)，蒙特卡罗采样1次，重力异常观测误差标准差为2 mGal，采用粒子群优化算法后，将惯导指示航迹整体平移，采用粒子滤波算法，得到匹配结果如图7所示。图8示出了粒子滤波算法和联合算法的匹配航迹结果差异，可见，联合算法对初始段航迹具有明显改善作用；当重力异常观测误差标准差为5 mGal时，得到匹配结果如图9所示，图10示出了两者间差异，可见，联合算法能够在一定程度上降低实测重力异常误差对匹配导航结果精度的负面影响。

图7 观测误差标准差2 mGal时，联合方法匹配航迹结果

图8 观测误差标准差2 mGal时匹配导航结果精度比较

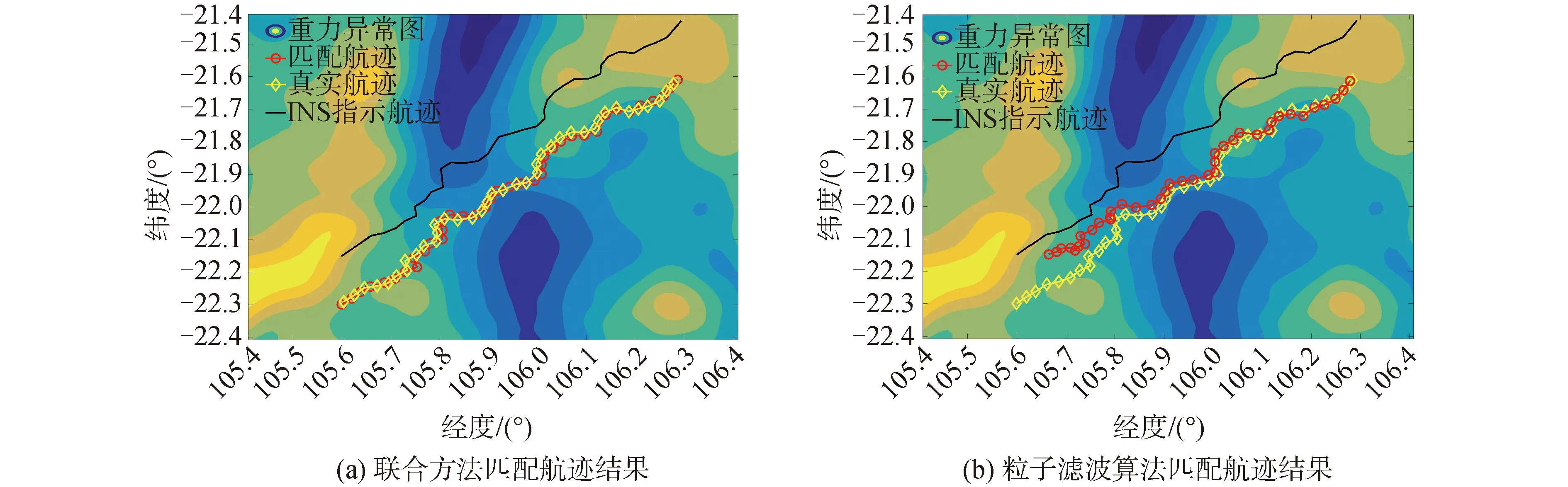
图9 观测误差标准差5 mGal时匹配航迹结果

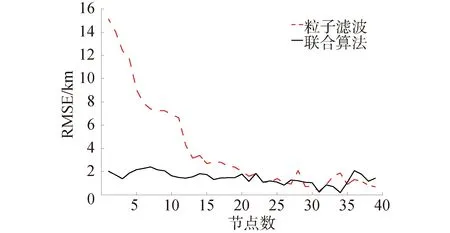
图10 观测误差标准差5 mGal匹配导航结果精度比较

4 结论

1)本文将粒子滤波算法应用于水下重力匹配导航，首先分析了不同蒙特卡罗采样样本量、不同重力异常观测误差标准差、以及不同初始偏差3种工况对匹配导航精度的影响。

2)初始偏差较大时，对其进行改善有助于提升初始段匹配精度；初始偏差较小时，采用多次蒙特卡罗计算对提高精度的帮助作用不大，初始偏差较大时，单次蒙特卡罗采样的计算精度会有所下降，多次蒙特卡罗采样提升精度的同时降低了匹配导航工作效率。

3)实测重力异常观测误差标准差越小越好，然而，当误差标准差增大，缩小初始偏差有助于减小其负面影响。

4)综上可以看出，采用粒子群优化和粒子滤波的联合算法能够对初始偏差进行改善，有助于进一步提高精度、提升效率、增强可靠性，通过算例，进一步验证了该方法的可行性和有效性。