双层系统内Jeffreys流体的Rayleigh-Marangoni对流不稳定性分析

栾 致 漫

(南京航空航天大学 数学系, 南京 210016； 南京航空航天大学 飞行器数学建模与高性能计算工业和信息化部重点实验室, 南京 210016)

双层系统中的Rayleigh对流稳定性问题在工程领域应用广泛, 如地热水库、 地下水流动、 生物材料和核电厂的散热等[1-7]. Nield[1]研究了底部加热的多孔层-流体层的线性稳定性问题, 并考虑在可变形上表面的表面张力效应, 得到了恒定热通量边界条件的解; Chen等[2]研究了流体-多孔介质系统中的指状对流, 结果表明, Rayleigh数与波数的曲线为双模态, 即存在2个局部最小值, 当厚度比较小时, Rayleigh对流不稳定性主要由多孔层主导, 当厚度比较大时, Rayleigh对流不稳定性主要由流体层控制； Straughan[3]利用Jones条件和Beavers-Joesph条件组成系统中交界面处的边界方程, 通过改变多组物理参数, 分析了双层系统中的热稳定性； Chang[4-5]分析了双层系统中Couette流和Poiseuille流的Rayleigh对流的线性稳定性, 利用Chebyshev tau-QZ方法获得相关数值结果, 并讨论了水平方向与垂直方向稳定性的差异； Samanta[6]用Darcy-Brinkman方程描述了多孔层的流动, 进而考察了双层系统的Couette流-Poiseuille流的稳定性问题, 并分析了厚度比对流体层和多孔层稳定性的影响； Kolchanova[7]研究了失重状态下双层系统发生高频纵向振动时Rayleigh对流的产生, 结果表明, 对流速度与厚度比有关; Block[8]认为薄液层中的表面张力导致对流细胞改变; Pearson[9]认为薄液层中的表面张力梯度产生了对流, 这种由表面张力驱动的对流称为Marangoni对流; 刘秋生[10]比较了在流体-流体双层系统中Marangoni对流与热毛细对流的不稳定性, 通过数值模拟可知, 稳定状态与界面张力温度系数有关; 刘荣等[11-12]对带有蒸发界面的双层系统进行了Rayleigh-Marangoni对流的稳定性研究, 结果表明, 增大蒸发速率, 不稳定性集中于液体层的底部界面, 蒸发系数对汽-液双层系统的影响较大; Liu等[13]通过考虑不同的厚度比, 研究了流体-多孔介质系统中Rayleigh对流和Marangoni对流耦合模式的不稳定性； Zhao等[14]分析了流体-多孔介质系统中自由表面传热条件对Rayleigh-Marangoni不稳定性的热效应, 结果表明, 不稳定性模态转变仅出现在表面张力较强的条件下； Yin等[15]研究了双层系统中Oldroyd-B流体的热不稳定性, 并通过不同的参数对比分析稳态对流与振荡对流; 康建宏等[16]分析了多孔介质内黏弹性流体的Rayleigh对流稳定性; Yin等[17]研究了双层系统中黏弹性流体的热不稳定性; Patne等[18]研究了Jeffreys流体中的Marangoni不稳定性; Sarma等[19-20]讨论了在可变形和不可变形上表面Maxwell流体的Marangoni不稳定性; 章绍能等[21]对温度不均匀界面上黏弹性液滴的单层系统进行了流动稳定性分析, 其中考虑了流体弹性因素的影响, 结果表明, 当Prandtl数较小时, 液体层趋于稳定模态; Madhukesh等[22]研究了在化学作用下Casson纳米流体的Marangoni对流, 通过改变温度、 微生物和浓度等因素分析了流动的稳定性; Li等[23]研究了混合纳米流体中的Marangoni对流问题, 将Darcy-Forchheimer流添加到动量方程中, 并在热方程中分析了具有非线性热源汇与热辐射的影响. 但上述研究仅讨论了Rayleigh对流和Marangoni对流的单一对流现象, 并未同时考虑两类对流.

本文在上述研究工作的基础上对比了Rayleigh对流和Marangoni对流, 并将两类对流耦合, 研究流体-多孔介质双层系统中非牛顿流体的Rayleigh-Marangoni对流不稳定性问题. 通过线性稳定性将3维偏微分方程组简化为常微分方程, 在振荡对流下, 分析应力松弛时间、 应变弛豫时间、 上表面传导对流特性和厚度比对Rayleigh对流和Marangoni对流的影响.

1 数学模型

图1为流体-多孔介质双层系统的示意图. 考虑覆盖在多孔层z∈(-dm,0)的非牛顿流体层z∈(0,d)组成的流体-多孔介质双层系统, 流体层和多孔层的交界面设为z=0.多孔层底部温度设为TL, 流体层的上边界是一个没有任何变形的自由表面, 温度为TU, 交界面处温度为TI.温度关系满足TL>TI=Tex>TU. 流体层和多孔层充满了黏弹性流体(Jeffreys流体), 其本构方程[24-26]为

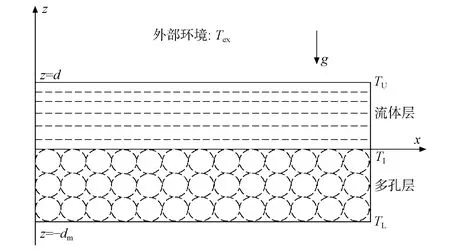
图1 流体-多孔介质双层系统的示意图

本文引入了Boussinesq近似, 当流体运动中温度变化很小时, 其密度变化也很小, 由于运动由浮力诱导产生, 因此不考虑浮力时可略去密度变化.将密度函数ρ(T)进行Taylor展开, 且保留至一阶项, 即满足

ρ=ρ0[1-β(T-T0)],

(2)

其中ρ和ρ0分别是温度为T和T0时的密度,β为常体积膨胀系数.

1.1 控制方程

其中p为压力,g为重力加速度,T为温度,κf为流体层中的热扩散率.

其中um为多孔层的速度,φ为孔隙度,pm为多孔层的压力,K为渗透率,Tm为多孔层的温度,κm为多孔层的热扩散率,Gm=[φ(ρ0cp)f+(1-φ)(ρ0cp)m]/(ρ0cp)f为多孔层与流体层的比热容比.

基本状态方程为

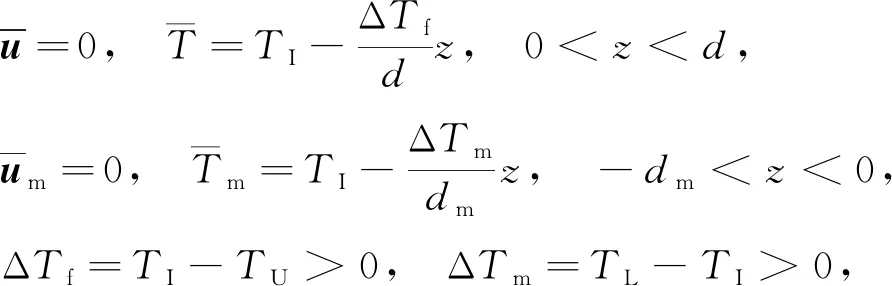
(9)

为研究系统的稳定性, 对系统施加一个小的扰动, 于是在基本状态方程(9)中加入一个扰动项

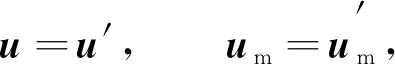
(10)

(11)

(12)

将方程(10)～(12)代入方程(3)～(8)中, 可得流体层和多孔层的线性化控制方程.为便于观察, 省略扰动的上标, 对动量方程进行两次旋度运算以消去压力项π和πm.为得到无量纲方程, 分别在两层中引入如下尺度： 在流体层中, 长度的尺度为d, 速度的尺度为ν/d, 时间的尺度为d2/κf, 温度的尺度为νΔTf/κf； 在多孔层中, 其尺度分别对应其中ν=μ/ρ为运动黏性系数.

因此, 对于流体层, 无量纲控制方程为

对于多孔层, 无量纲控制方程为

1.2 边界条件

在多孔层的底部z=-1处, 边界条件为等温边界条件

wm=0,Tm=0.

(17)

在流体层的顶部z=1处, 具有表面张力的边界假设为不可变形且隔热, 总切向力由剪切力补偿, 于是可得

w=0,DT+BiT=0,

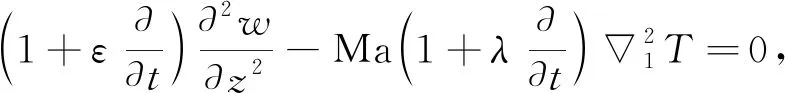
(18)

在交界面z=0处, 速度、 温度和热通量分别为

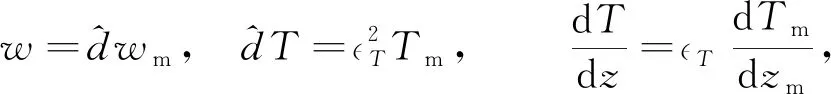
(19)

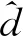
切向应力边界条件[27]为

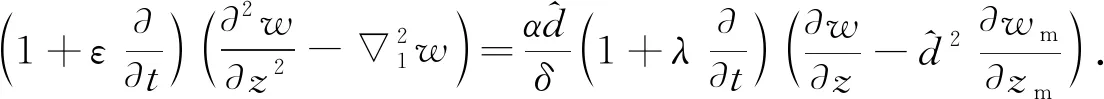
(21)

无量纲参数关系为

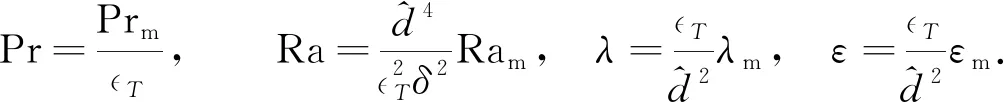
(22)

2 简正模态

利用简正模态方法, 可将扰动量表示为

(23)

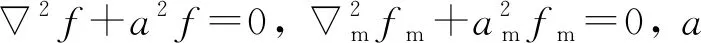
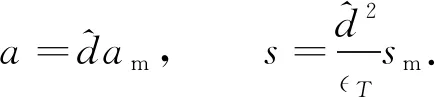
(24)

将方程(23)代入方程(13)～(16)中, 控制方程变为

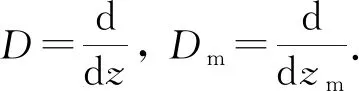
简正模态的边界方程为

(31)

流体层的顶部有3个边界条件, 多孔层的底部有2个边界条件, 流体层和多孔层的交界面有5个边界条件.这是一个由方程(25)～(28)和边界条件(29)～(31)组成的10阶微分方程, 下面求解其中的Rayleigh数和Marangoni数.

3 数值方法

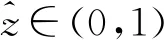
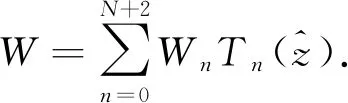
(32)

因此, 问题转化成求解广义特征值问题AX=RamBX或AX=MaBX, 其中A和B均为5(N+3)×5(N+3)矩阵,X=(W,Q,Θ,Wm,Θm)T,Q=(D2-a2)W.如求解特征值Ram, 矩阵A和B的表达式为

(33)

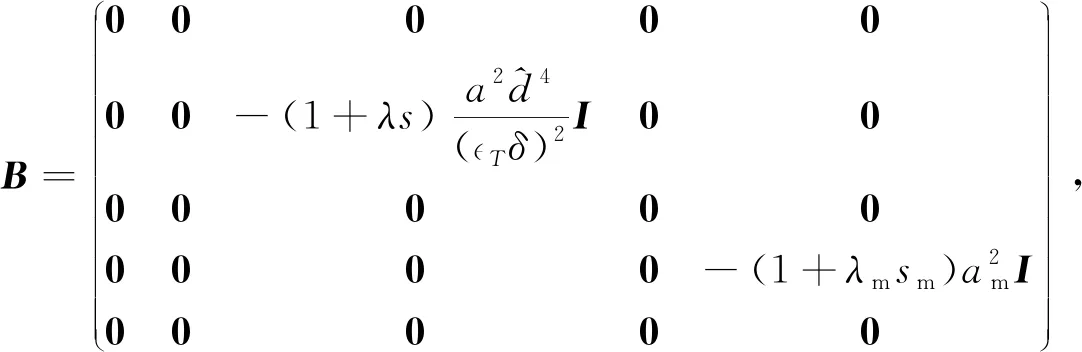
(34)

其中

4 结果与讨论

不同N值的数值结果对比列于表1, 分别选取基函数个数N=5,10,16,25计算其临界值以验证该算法的收敛性.结果表明,N=10后的数值结果已基本稳定, 且随N的增大更精确, 同时考虑处理时间和效率, 选取N=16进行计算.

表1 不同N值的数值结果对比

4.1 应力松弛时间对Rayleigh-Marangoni不稳定性的影响

不同应力松弛时间的Rayleigh对流如图2所示. 由图2可见: 在振荡对流下, 较小的应力松弛时间可获得较高的波数-Rayleigh数曲线; 长波和短波区间分别存在一个极小值, 即Rayleigh数曲线呈双模态; 由于左分支的最小值小于右分支的最小值, 因此系统的不稳定性由长波分支控制, 即Rayleigh对流在多孔层中开始进行并由其主导； 振荡对流的临界Rayleigh数随应力松弛时间的增大而减小, 表明弹性越大的非牛顿流体会加剧Rayleigh对流, 使系统变得更不稳定.

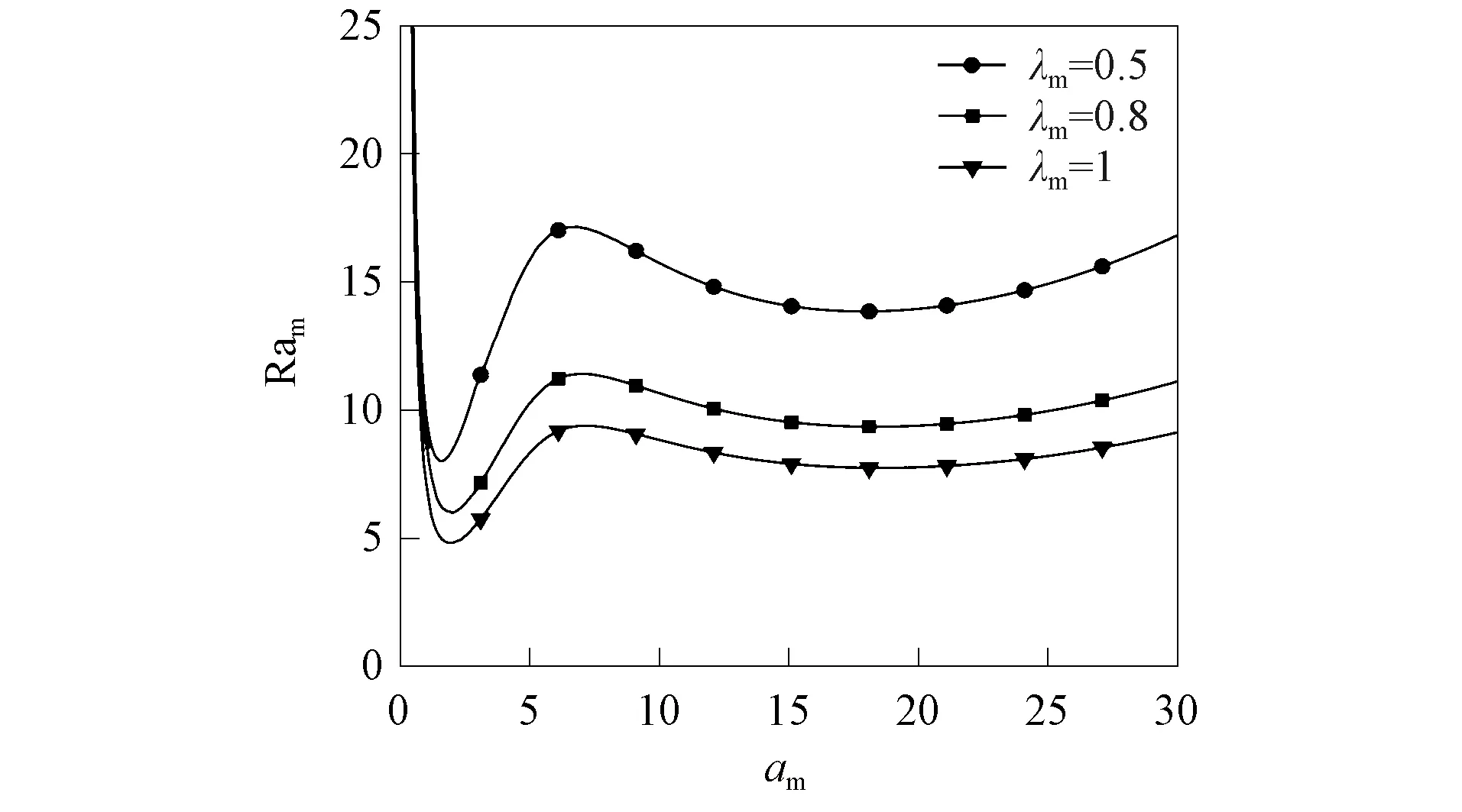
图2 不同应力松弛时间的Rayleigh对流

不同应力松弛时间的Marangoni对流如图3所示. 由图3可见, 振荡对流下的临界Marangoni数曲线随应力松弛时间的增加而减小, 每条曲线在全局波数范围内只有一个最小值, 即Marangoni对流下的波数-Marangoni数曲线呈单模态, 且当Marangoni数取最小值时均在短波区间, 表明Marangoni对流只发生在流体层中, 而多孔层相对较稳定.

4.2 应变弛豫时间对Rayleigh-Marangoni不稳定性的影响

不同应变弛豫时间的Rayleigh对流如图4所示. 由图4可见: 波数-Rayleigh数曲线随应变弛豫时间的增加而上升, 应变弛豫时间提高了Rayleigh对流的稳定性, 表明黏性越小的非牛顿流体越容易导致系统内对流的不稳定性; Rayleigh数曲线呈双模态； Rayleigh对流不稳定性由长波分支控制, 仍在多孔层中发生并由其主导, 流体层较稳定.

图4 不同应变弛豫时间的Rayleigh对流

不同应变弛豫时间的Marangoni对流如图5所示. 由图5可见, 波数-Marangoni数曲线随应变弛豫时间的增加而上升, Marangoni曲线呈单模态, 每条曲线的Marangoni数最小值均在短波分支区间, 即Marangoni对流不稳定性在流体层中出现并由其控制.

图5 不同应变弛豫时间的Marangoni对流

4.3 导热性对Rayleigh-Marangoni不稳定性的影响

不同Biot数的Marangoni对流如图6所示. 由图6可见: 与Biot数大小无关, Marangoni曲线呈单模态, 且不稳定性均受流体层控制； 临界Marangoni数随Biot数的增加而增加, 当Bi→+∞时, 根据图像可推测Ma→+∞, 即在上表面导热性良好时, 表面张力效应可视为消失.

图6 不同Biot数的Marangoni对流

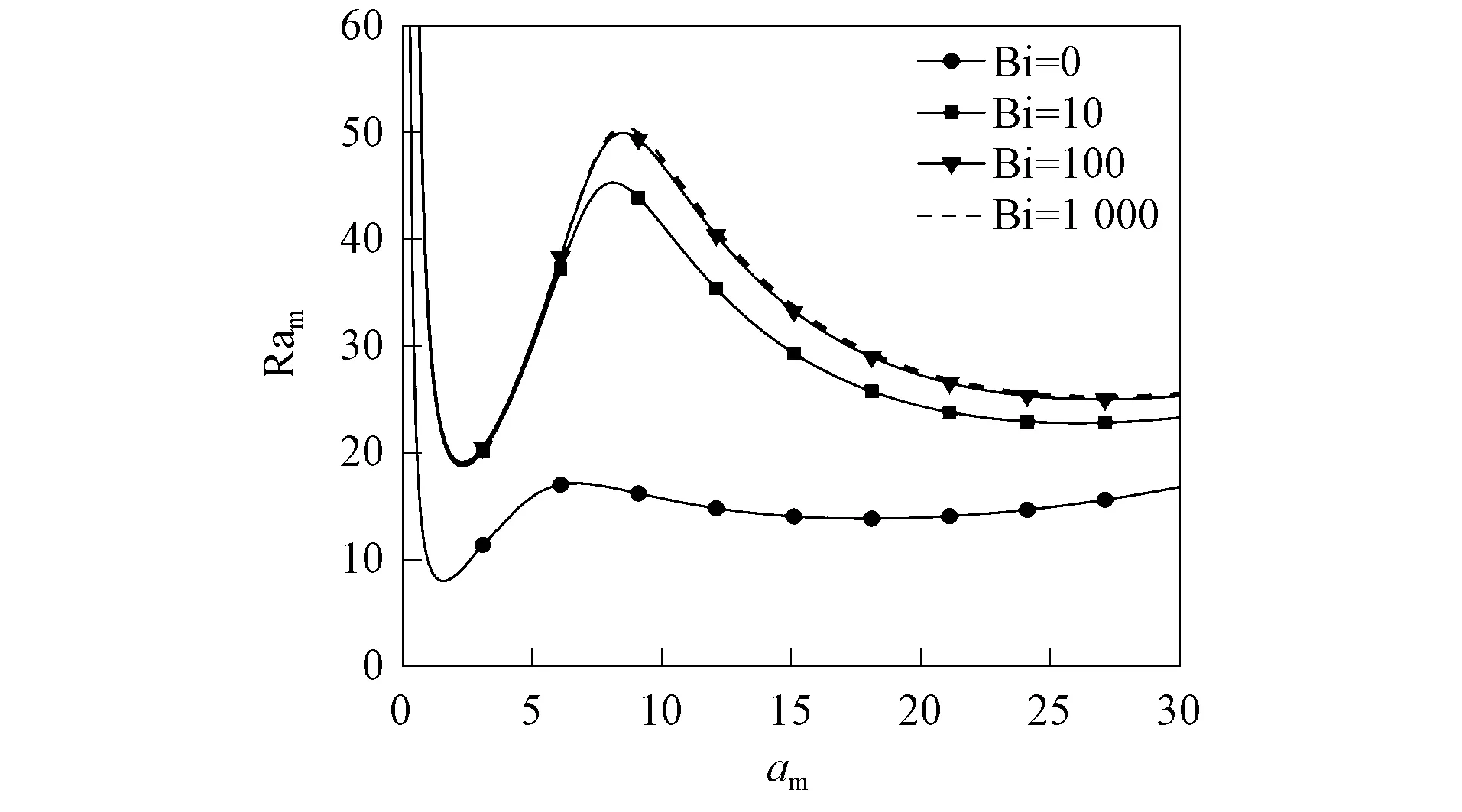
图7 不同Biot数的Rayleigh对流

4.4 厚度比对Rayleigh不稳定性的影响

图8 不同Biot数的Rayleigh对流

4.5 耦合模式下Rayleigh-Marangoni对流的不稳定性

不同Marangoni数的Rayleigh-Marangoni对流耦合模式如图9所示. 由图9可见: 当Marangoni数减小时, Rayleigh数曲线呈下降趋势, 表明Marangoni效应减弱会增强耦合模式下系统Rayleigh对流的不稳定性； 中性曲线呈双模态, 左分支均低于右分支的最小值； 当增大Marangoni数, 短波分支的Rayleigh数的最小值逐渐变大, 即流体层的Rayleigh对流会趋于稳定, 因此Rayleigh对流不稳定性均以长波为主, 即对流发生在多孔层中.

图9 不同Marangoni数的Rayleigh-Marangoni对流耦合模式

综上, 本文研究了一类物理参数对Rayleigh-Marangoni对流稳定性的影响. 采用MATLAB对Rayleigh数和Marangoni数的求解进行数值模拟, 讨论各参数对两类对流稳定性的增强或破坏作用. 结果表明: 黏性越大的流体和系统上表面具有越良好导热性能均有利于加强对流的稳定性, 而弹性越大的流体会降低其稳定性; 适当增加厚度比, Rayleigh对流不稳定性的主导分支将发生转变; 耦合模式中越大的Marangoni效应将促进Rayleigh对流的稳定性.