基于客流特征鉴别的公交跨线组合调度优化方法
2022-11-20翁剑成王茂林林鹏飞马思雍徐立泉梁发军
翁剑成 王茂林 林鹏飞 马思雍 徐立泉 梁发军
(1.北京工业大学北京市交通工程重点实验室,北京 100124;2.北京工业大学信息学部,北京 100124;3.北京中医药大学中医学院,北京 100029;4.北京公交集团运营调度指挥中心,北京 100055)
2019 年9 月,国务院印发《交通强国建设纲要》,提出推进出行服务快速化、便捷化发展,优先发展城市公共交通,鼓励引导绿色公交出行[1]。交通运输部印发的《公交都市考核评价指标体系》中,公共交通出行分担率、正点率、乘客满意度等成为评价城市的公交发展的重要指标[2]。然而近年来,地面公交在所有交通方式中所占比重却呈现连续下降趋势,以北京为例,地面公交出行占比从2016 年的15.6%下降到2020 年的11.7%[3]。传统以公交线路、车队为组织单元的公交运营调度模式,存在的运行效率不高、运营管理层级多、线路间缺乏协同和资源有效整合等问题,影响了公共交通服务水平和乘客满意度的提升。随着城市规模的扩张,单纯增加设施供给来满足交通出行需求是不可持续的发展策略,我国应充分整合利用城市公共交通系统现有资源,提高公交运营效率与服务能力,以适应城市空间增长[4]。因此,如何在公交客流时空不均衡的背景下,有效整合现有公交运力资源,提升公交线路的运营组织效率,改善公共交通服务的满意度和服务能力,成为亟待解决的技术性需求[5]。面对人车线路资源利用效率不高的问题,北京公交在公交区域调度行动方案中就明确提出,根据区域内公交线路的客流时空规律,在具备条件的多线路间实施不同层面的跨线联运和统筹调度[6]。与此同时,海量的公共交通运行数据的获取,为基于实际数据驱动的公交线路调度优化提供了重要的条件支撑。
在公交运营调度优化研究方面,国内外学者针对单线或组合线路,单车型或多车型混合的发车频率优化等内容开展了广泛研究。巫威眺等[7-9]以单条公交线路为研究对象,针对线路客流分布的不均衡性,建立公交组合调度与购车计划的双层规划模型,对全程车和区间车的发车频率优化,探讨了运营预算限制对优化调度的影响。Ibarra-Rojas等[10]为平衡服务水平和运营成本,针对时间表和车辆调度问题,建立整数线性模型求解帕累托最优解集合,解决多条线路的运营问题。滕靖等[11]对纯电动公交车的时刻表构建多目标优化模型进行优化,考虑了续航里程以及车辆数量约束,对车辆排班进行优化。刘畅[12]建立了一个上下行发车频率不同的公交组合调度模型,以粒子群算法和模式搜索算法相结合的混合启发式算法进行求解。姚恩建等[13]考虑客流的时变性特点,在混合不同公交车型的情形下,同步优化车型配置和发车间隔,结合枚举法和NSGA-Ⅱ算法对模型进行求解。Sun等[14]建立了多种车型(大型车、小型车、混合动力车)的优化调度模型,并采用启发式算法求解,满足了客流的弹性需求。
部分研究人员也针对多线路的公交组合调度优化方法进行了研究。杨信丰等[15]为提高对乘客服务水平的同时降低公交运营成本,构建区域公交协调调度双层模型,下层通过车辆满载率优化运营成本,上层模型考虑服务水平优化发车时刻,优化后在拥挤程度、候车时间、换乘时间方面均有不同程度的改善。Gkiotsalitis 等[16]为解决公交高峰运营需求分布不均匀和资源稀缺的问题,考虑在线路中的最优站点设置区间车,利用外部点惩罚的方法将约束优化问题近似为无约束优化问题,并采用遗传算法进行求解。Ceder 等[17]在设定的公交线网中,为方便乘客换乘,在换乘点让乘客候车时间最短,制定了一个最大程度同步的公交线网时刻表。Schmid等[18]提出了带时间窗和均衡出发时间的车辆调度问题,目标是通过允许小班次的服务班次的出发时间来最小化公共交通的运营成本,期望得到高质量的时间表。
综上所述,国内外学者针对公交调度优化方面的研究,主要根据乘客出行成本、公交运行成本或司乘人员工作时长等约束,对公交时刻表进行优化;跨线路的组合调度优化方面,则主要集中在多条线路的联合时刻表编排或引入区间车的调度策略。但对于车辆满载率、发车间隔等约束的考虑还存在明显不足,较少涉及针对区域内具有客流互补特征的多条公交线路开展联合运营调度优化。
本文拟通过对公交线路运营特征时空差异性的挖掘,提出跨线调度的模式及线路的识别与组合条件,并通过跨线组的发车时刻表确定跨线调度的车辆数,以乘客出行和公交运营成本最小为目标,设计多车场的跨线调度优化模型,引入改进的遗传算法对优化模型进行求解,输出被支援线路的发车时刻表和跨线联合调度方案,并拟通过北京市的实际案例,对所提出的模型有效性进行验证。
1 公交跨线调度组鉴别方法
跨线调度是公交区域调度的一种特定情景,多条线路共用人车资源,从而使运营效能得到最大化地提升,但跨线调度对于可以组合的线路有较高的要求,需要根据不同线路客流在时间、空间、方向上的差异,将已完成客流高峰时段的L1线路(支援线路)的冗余运力向持续高客流、运力紧张的L2线路(被支援线路)转移,L1线路有部分车辆跨线到L2线路运营,在L2线路完成一次或多次周转后,在L1线路再次进入客流高峰时段前返回L1线路运营。其中Y1和X为线路L1的起始场站,Y2和Z为线路L2的起始场站。基于跨线调度的技术要求与客流特征,本节提出了跨线调度的线路组识别规则以及各运营时段跨线车辆数确定方法,路线调度示意图如图1所示。
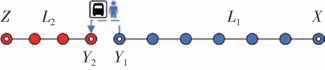
图1 跨线调度示意图Fig.1 Schematic diagram of cross-line scheduling
1.1 跨线调度的线路组识别规则
基于公交线站空间关系和公交客流数据,识别跨线调度线路组。当两条或多条公交线路的起终点相同或距离较近、高峰时段相异、一条线路存在分方向的配车需求差、另一条线路到站时间稳定性低时,两条线路适宜组合。线路的识别与组合规则如下。
(1)支援线路L1与被支援线路L2起终点距离d1小于阈值
L1和L2两条线路起终点的距离不能过远,以保证跨线车辆转场时间短,转场耗时及成本才能尽量小。一般要求,两条线路起点或终点的实际路径距离D(Y1,Y2)小于2 km。
(2)线路的客流高峰时段相异
高峰时段与平峰时段所需车辆存在较大差异,当公交线路的高峰时段不同且存在互补性时,可以将支援线路L1非高峰时段的车辆跨线到被支援线路L2运行。

式中,TA12为线路L1的客流高峰时段,TB12为线路L2的客流高峰时段。
(3)支援线路L1存在分方向的配车需求差异
支援线路L1双向存在配车需求差异,尤其是当L1线路为通勤、通学等干线线路时,线路客流的方向不均衡系数较大。当分方向配车需求差大于一定阈值时,可以将配车需求少的方向的车辆跨线到其它公交线路运营。
(4)被支援线路L2发生大间隔的比率较高
线路大间隔比率高,说明公交线路运营大间隔发生次数多,公交间隔匀整度较差,需要引入跨线调度后优化发车频率,减少大间隔的发生概率。
1.2 各运营时段跨线车辆数的确定方法
跨线调度的车辆来自支援线路L1,加入到被支援线路L2。假设L1、L2两条线路发的都是全程车,无区间车和大站快车等其它调度方式,各运营时段跨线车辆数的确定方法如下。
步骤1根据L1线路的公交行车计划表计算L1线路每辆公交车在Y1场站的停站驻车待发车时间。

式中,tAY1m为车辆m在L1线路Y1场站的停站驻车待发车时间,TAY1d为车辆m在L1线路Y1场站第k次发车时间,TAY1k为车辆m在L1线路第k-1次到达Y1场站的时间。
步骤2假使车辆m可以跨线,计算车辆m在L2线路的跨线运营时间。

式中,tkx为车辆m跨线运营时间,tjq为车辆m在L1线路Y1场站加燃油或充电时间,tY1Y2为车辆m从Y1场站跨线前往到Y2场站时间,tbx为车辆m在场站变线路名称及调整费率卡时间,tBY1Z为L2线路i时段从Y1场站到Z场站方向的单程时间,tBZY1为L2线路i时段从Z场站到Y1场站方向的单程时间,tBZ为车辆m在L2线路Z场站的停站时间,tBY2为车辆m在L2线路Y2场站的停站时间,Tnum为车辆m在L2线路跨线运行的周转次数。当Tnum=1 时,tkx最小,即满足L2线路一个周转时间,可跨线到L2线路运营一个车次。
步骤3通过比较tAY1m和tkx的大小关系,判断车辆m是否可以跨线运营,并确定车辆m的跨线运营周转次数。当tAY1m≥tkx时,车辆m可进行跨线调度,计算Tnum的最大值,得出车辆m可以在L2线路上跨线运营周转的次数;当tAY1m 步骤4确定跨线运营时段L1线路可加入到L2线路的跨线车辆数pmj,为L2线路的时刻表优化提供支持。 在线路组合鉴别与跨线车数量确定后,本文考虑了线路车型容量差异、运营成本差异和各运营时段可加入的调度车辆数差异,以乘客出行成本和公交运营成本之和最小为优化目标,分时段的发车车型和发车间隔为优化变量,建立L2线路的公交跨线组合调度优化模型。 为简化问题,使得模型更加具有普适性,提出如下的假设: (1)不考虑道路运行状况的影响; (2)车次均为全程车,不考虑大站快车、区间车等特殊调度方式; (3)同一线路使用相同车型,载客量相同; (4)各车次严格按照公交时刻表运行,无中途停车或者掉头返回的情况; (5)同一时段内,线路各站点的乘客到达率服从均匀分布; (6)在公交站点候车的乘客均能一次上车,不存在因满员而滞站的情况。 模型中所涵盖的参数较多,在此一并列出,各参数的符号、定义及单位见表1。 表1 模型参数及定义Table 1 Model parameters and definitions 跨线调度的优化方案要兼顾公交出行者和公交公司双方的利益,目的在于使乘客出行成本和公交运营成本最小,总成本为两部分成本的加权求和。 (1)乘客出行成本 乘客出行成本包含乘客候车时间成本和乘客在途成本两部分。 乘客候车时间成本C11与发车间隔和乘客到达率有关。这里采用变间隔的非均衡发车模型,第k辆车与k-1辆车的发车间隔设为Δtk,为使模型求解的Δtk的结果可操作性强,Δtk取整。假设乘客站点到达率近似服从均值分布,则在j时段一辆公交车在站点i的上车乘客数量Pi和在站点i′的下车乘客数量Qi′为 在j时段共发K辆车次,因此乘客j时段乘客候车时间成本为 由于在途时间主要受到途经路段的拥堵状况影响,在此引入车内的拥挤程度来表征乘客的在途成本。乘客车内拥挤成本由在公交车内满载率决定,站立乘客越多,产生的拥挤成本就越大。模型中规定车内拥挤会产生惩罚系数ε,惩罚系数的大小与车辆站间满载率Bi有关,车辆在站间的满载率Bi大于设置的公交车满载率临界值Bo时才会产生拥挤费用。产生的乘客拥挤成本为j时段所有车辆的拥挤成本之和。 式(9)中Si-d即为车内的站立乘客数量,其中站点间的路段通过量Si由前一站点的路段通过量和站点上下车乘客数量决定。 式(9)中fi用于判断车辆是否会产生乘客拥挤成本,只有当车辆在站间的满载率Bi大于设置的公交车满载率临界值Bo时才会产生拥挤费用。Bi为车辆在站点i的区间满载率,由车内乘客人数和公交车的额定载客量e(为该车型座位数和最大站立的人数总和)的比值求得。 跨线车辆与原车辆座位数与额定载客量有可能不同,产生的拥挤成本不同,因此j时段乘客出行的总成本为乘客乘坐跨线车辆的出行成本与原车辆的出行成本之和: γk为0-1 变量,当第k辆车为跨线车辆m时,γk=1;当第k辆车为L2线路原车辆时,γk=0。 (2)公交运营成本 公交运营成本包含跨线车辆转场成本、线路车辆运营成本及车辆固定折合成本。 其中跨线车辆由Y1→Y2场站的转场成本为 车辆运营成本由每公里的运营成本和车辆运行的公里数决定,两种车辆的运营成本之和为 车辆固定折合成本CBp是指L2线路原车辆的购置、维修、保养的折合成本。 因此公交公司运营总成本为 为了加快求解速度,获得准确的求解,对模型的相关参数设置了以下约束: 式(18)和式(19)表示在j时段内线路发出的车辆数量要不大于线路的配车总数量;式(20)表示公交车辆发车间隔满足介于最大发车间隔ΔTmax和最小发车间隔ΔTmin之间;式(21)表示j时段内发出的所有公交车发车间隔的总和不大于j时段的总时间Tj;式(22)表示乘客候车时间成本系数α以及公交运行成本系数β的约束。 前述跨线组合调度优化模型为多变量、非线性、多约束的最优化问题,属于NP-hard 问题,需要采用启发式算法求解。目前比较常用的启发式算法有模拟退火算法、禁忌搜索算法、遗传算法、蚁群优化算法等[19-22]。遗传算法具有鲁棒性强、适应性强的特点,有较强的全局搜索能力,主要求解步骤分为编码、选择、交叉、变异[23]。本文以发车间隔为最小的决策单元,易于编码,问题的形式与遗传算法相对贴近,因此引入遗传算法作为公交跨线组合调度优化模型的求解算法。求解的主要步骤如下。 (1)生成随机发车间隔 调度优化时段j共Tjmin,按发车间隔时间的约束条件,在Tj内随机生成发车间隔Δtk,使得Δtk的总和为Tj,如表2所示。 表2 发车间隔生成示例Table 2 Example of the departure interval (2)编码 采用二进制编码方式,每一个时间间隔Δtk对应一个发车类型,其中1 对应着发L2线路原车辆,0 对应着发跨线车辆。图2 所示为调度优化候选解对应的染色体的示例,染色体长度为k,如表3所示。 表3 候选解对应的染色体示例Table 3 Examples of chromosomes corresponding to candidate solutions 图2 遗传算法交叉算子Fig.2 Crossover operator of genetic algorithm (3)种群初始化与适应度函数构造 确定初始参数:最大迭代次数T,种群规模N,交叉概率Pc,变异概率Pm。在确定了种群规模后,随机选择N组可行线路组合作为初始种群,此过程相当于在优化解空间中随机选择N个初始解,接着通过构建适应度函数来就个体对环境的适应能力进行评估。 式中,F(f(x))为适应度函数,f(x)为跨线调度优化模型的目标函数,x为跨线调度模型的一个可行解,Cmax为修正系数,通过计算跨线调度前的实际运营成本来对Cmax赋值。 (4)遗传算子操作 通过选择算子、交叉算子和变异算子这3个操作算子的运算,生成子代种群。 使用精英选择方式,保留进化到当前代最优的个体,并用其把选择复制后适应度值最小的个体替换掉,以达到保留最优个体并淘汰最劣质个体的目的。 然后选用单点交叉算子,两个父代染色体将数量相同的基因信息进行交换,产生新的子代染色体,可以避免个体中良好的基因片段被破坏,如图2所示。最后进行两点算子变异,根据变异概率Pm将变异区域的基因值取反,如表4所示。 表4 遗传算法变异操作Table 4 Genetic algorithm mutation operation (5)终止条件 预先设定迭代次数来控制运算的进行与终止,当算法迭代次数达到最大或者运算结果收敛时,算法终止。 选择北京公交668 路和122 路,线路及场站的位置如图3 所示,研究时段为8:30~10:30。此时122 路处于客流高峰时段,668 路为连接通州副中心和主城区的线路,客流具有明显的峰值突出和方向不均衡性特点,且该时段的客流高峰已过,有较多车辆在Y1场站驻车。由于公交线路的客流特征呈现一定的周期性规律,案例使用2019年1月中连续两周的公交运行数据,客流数据以及场站配车数据输入到模型中。通过识别发现各个指标项均满足识别规则,具体结果如表5 所示。并确定668 路为支援线路L1,122 路为被支援线路L2。根据两条线路的原始发车时刻表,估算确定能加入到122 路8:30~10:30运营的跨线车共7辆。 图3 公交线路走向示意图Fig.3 Schematic diagram of bus line direction 表5 668路和122路的跨线组合识别指标Table 5 Line 668 and line 122 crossover group identification indicators 在进行优化模型求解前,需要对站点间乘客出行OD 量、乘客候车的单位时间费用、公交车的固定成本等参数进行确定。 (1)站点间乘客出行OD量 模型中涉及到的乘客到达率是以真实的客流数据计算得到的,为该时段的OD 量与时段分钟数的比值。本文选取被支援线路122路两周工作日在8:30~10:30 时段的平均乘客出行OD 量数据,如表6所示。 表6 122路站点OD客流量示例Table 6 Example of OD passenger flow of line 122 between sta⁃tions (2)乘客候车的单位时间费用σ 北京市居民月平均工资收入为5 646 元/人[24],假设每天工作时间为8 h,每个月22 个工作日,计算得到单位时间乘客单位经济成本为0.53元/min因此乘客候车的单位时间费用的参考取值为σ=0.53。 (3)公交车的固定成本Cp 一辆公交车的固定成本Cp按一辆公交车一天的保养维修费用、折旧费用折合到运营小时中计算,一辆公交车购置费用为70 万元,使用年限为10 年,则一小时的折旧费用为7.99 元。公交车的保养维修费用为每天220元/辆。则车辆每小时的固定成本累计为Cp=22.66元/h。 (4)优化模型中其他参数 与此同时,结合北京公共交通运营实际情况的数据,对优化模型中车辆座位数、额定载客量、最大最小发车间隔、拥挤惩罚系数、车辆每公里的运营成本等相关参数进行赋值,参数取值见表7。 表7 模型设定的相关参数取值Table 7 Values of relevant parameters set by the model 运用MATLAB 软件求解模型,在求解过程中,当设置种群规模N=250,交叉概率Pc=0.8,变异概率Pm=0.05时,可以求得最优解。 优化后的发车类型及发车计划如表8所示,在8:30~10:30时段内,共发跨线车辆7辆,L2线路原车辆14辆,发车间隔5~7 min不等,L1线路跨线车与原车辆交替发车。 表8 优化的发车间隔及发车类型Table 8 Optimized departure interval and bus type 通过计算跨线调度优化前后的乘客出行成本和公交公司运营成本,如表9所示,可以看出乘客候车时间成本和车内拥挤成本都有明显的减少,乘客出行总成本减少了15%。加入跨线车辆后,L2线路由于减少了运营车辆数,原车辆的运营成本明显减少,而增加了跨线车辆的运营成本,但总运营成本减少了6%。跨线调度优化后,系统总成本由6 028元下降到5 327元,减少了12%。 表9 实行跨线调度前后成本变化Table 9 Cost changes before and after the implementation of cross-line scheduling 比较跨线调度优化前后平均候车时间、线路满载率、运能匹配度和客流强度这几项指标:在跨线调度前后122 路乘客平均候车时间缩短了11.8%,线路满载率减少了9.8%,乘客出行时效性和乘车舒适性都得到了改善;线路运能匹配度增加7.7%,调度优化后线路运力供给更贴合客流实际需求;由于加入跨线调度后调整了发车班次,线路客流强度也增加了8.7%,具体结果如表10所示。 表10 跨线调度优化前后运营效能指标变化Table 10 Operational performance index changes before and after cross-line scheduling (1)建立了基于客流特征鉴别的跨线组合调度优化模型,通过线路的起终点距离、高峰时段相异、配车需求差等条件设置跨线调度的线路组识别规则,线路的行车计划表以及跨线运营的时间设定确定了加入到各运营时段的跨线车辆数;以最小化乘客出行成本和公交运营成本为目标,建立公交跨线组合调度优化模型,设计了改进的遗传算法进行求解。 (2)选取北京公交668 路和122 路为对象开展实证研究。结果表明,与跨线调度优化前相比较,乘客候车时间成本和车内拥挤成本都有明显的减少,公交运营成本也有所降低。在运营效能的比较方面,调度优化后平均候车时间、线路满载率明显降低,运能匹配度和客流强度有所提升,乘客出行时效性和乘车舒适性都得到了改善。 (3)在公共交通运营公司普遍面临降本增效,提升人车资源利用效率的强烈需求下,研究从公交跨线组合识别规则制定,各时段跨线车辆数确定,调度优化模型建立求解,联合时刻表编制几方面开展了较完整的系统研究,所提出的模型更具有普适性,对于公交公司进行跨线调度优化的实践具有一定的参考价值。 实施基于跨线组合的公交调度策略有助于公共交通服务水平和乘客满意度的提升,未来的研究中,还可以对考虑公交动态调度及纯电动公交运营所带来的续航里程、充换电等约束,以进一步完善相关模型。2 公交跨线组合调度优化模型
2.1 模型的前提假设
2.2 模型目标函数



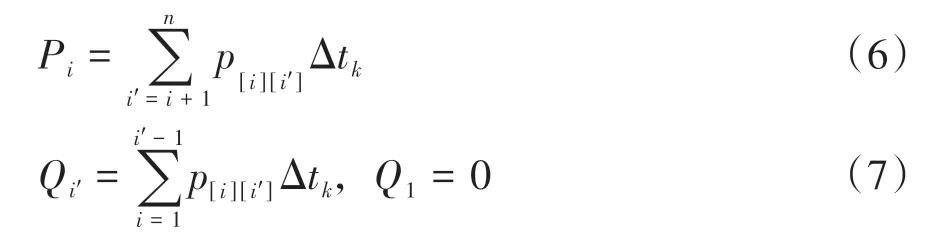
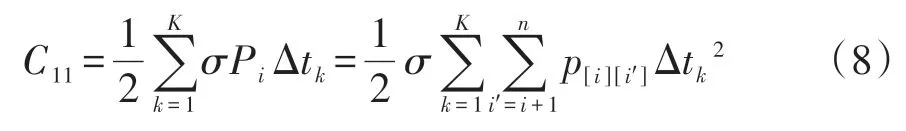
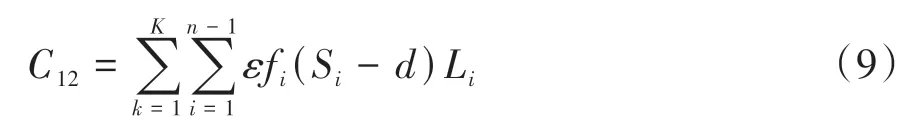

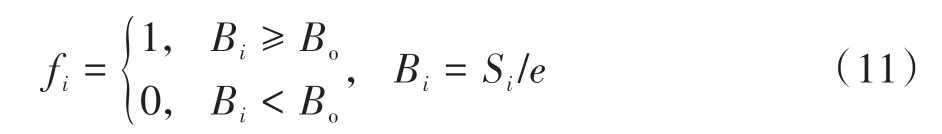
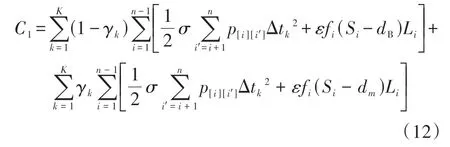




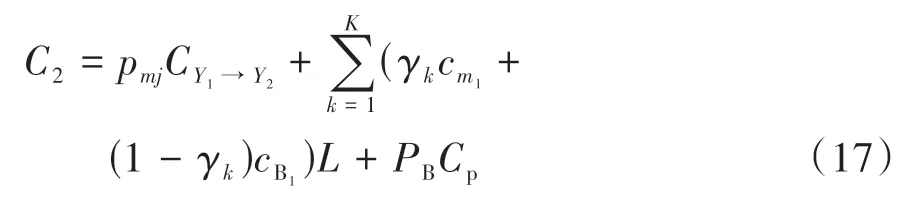
2.3 模型的约束条件

3 基于遗传算法的跨线组合调度优化模型求解

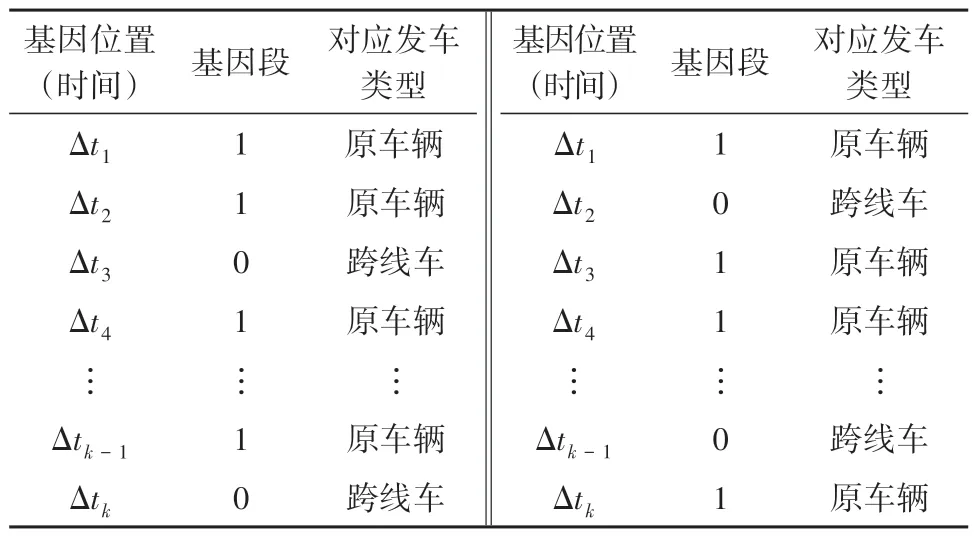

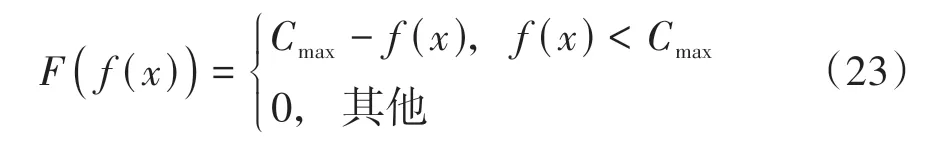
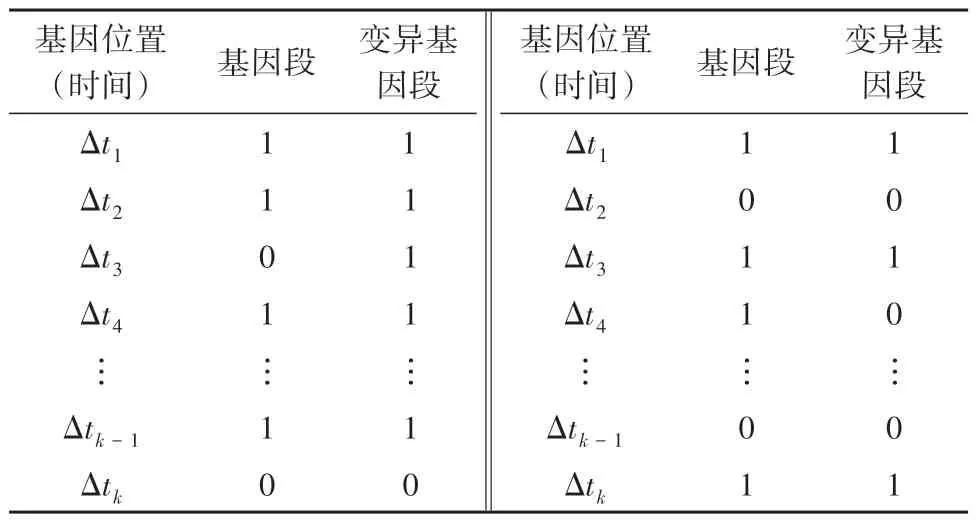
4 公交跨线组合调度案例分析
4.1 案例公交线路选择
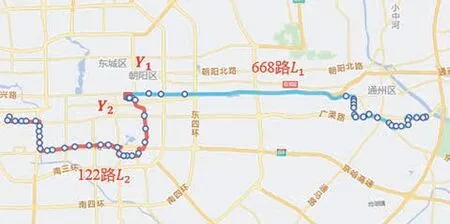

4.2 优化模型的参数确定
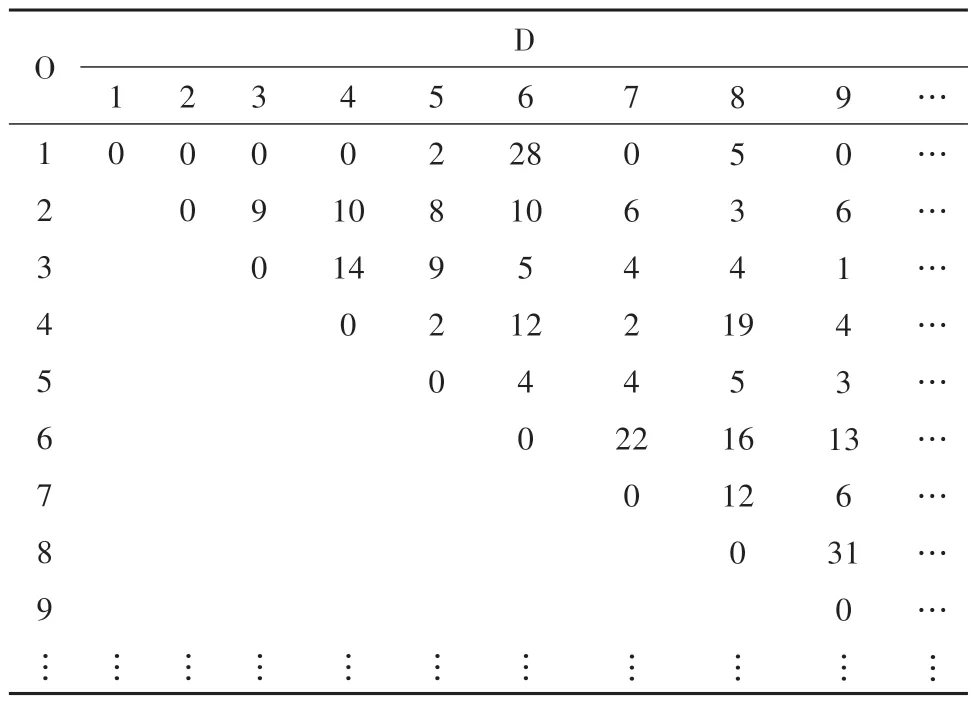
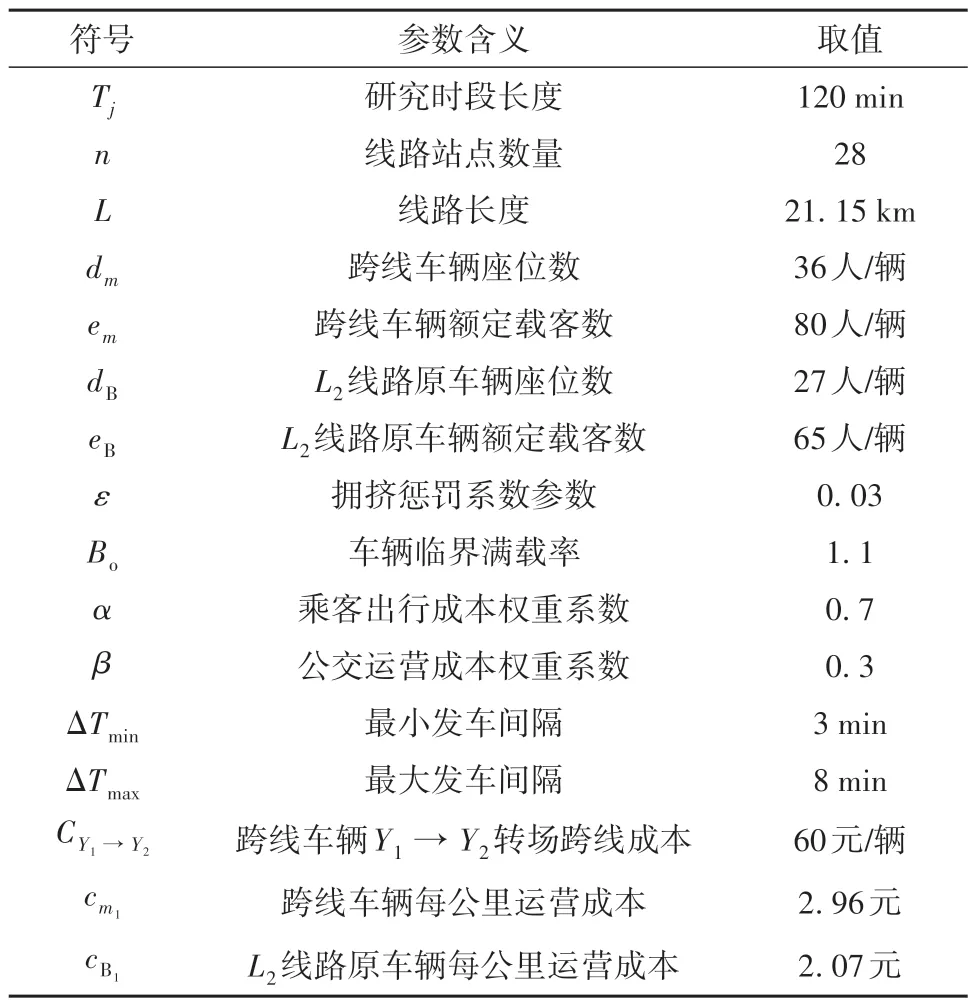
4.3 优化模型求解
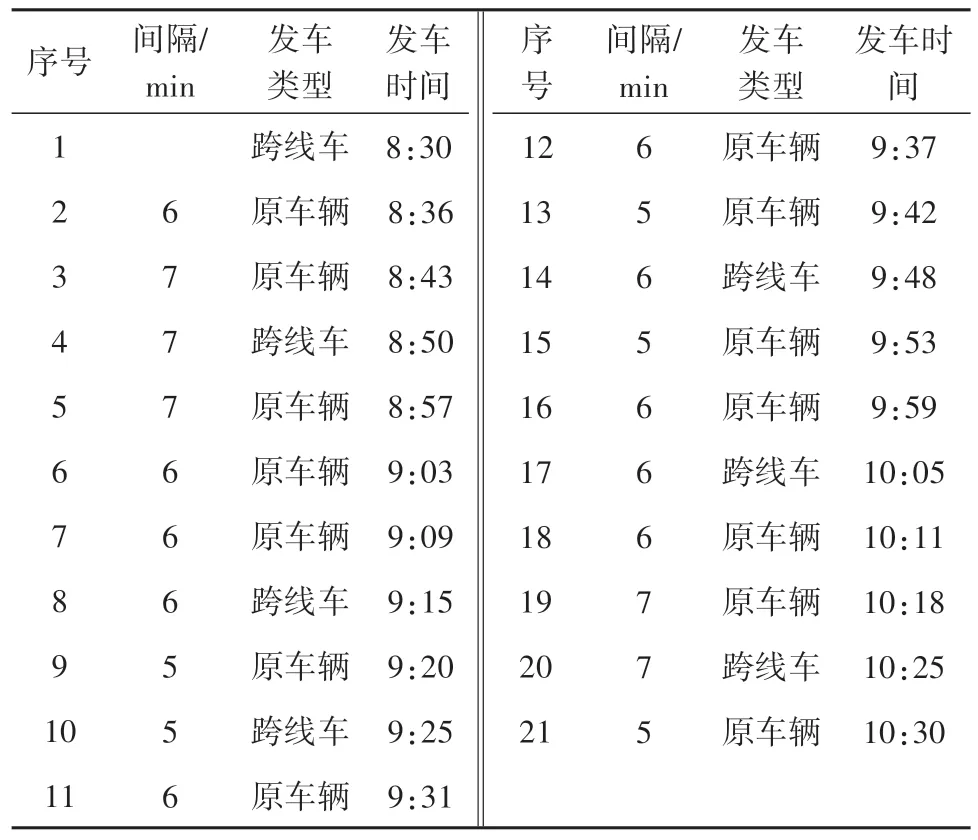
4.4 优化效果的评价

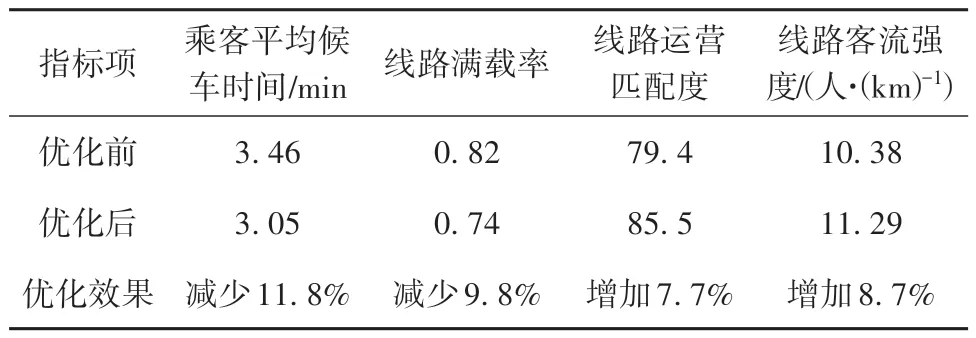
5 结语
