多停车场共享车位动态预约与分配优化模型
2022-11-20王元庆蔺思玉谢明辉王宏涛高亚楠
王元庆 蔺思玉 谢明辉 王宏涛 高亚楠
(1.长安大学运输工程学院,陕西西安 710064;2.长安大学生态安全屏障区交通网设施管控及循环修复技术交通运输行业重点实验室,陕西西安 710064)
城市机动车保有量的持续增长,导致停车难问题愈发严重,挖掘停车资源潜力、打破信息隔阂、提升停车效率变得愈发重要。有研究发现,寻求停车者,在市中心人均花费约8.1 min 的时间来寻找车位,而这个过程会造成30%的路网交通拥堵。这样会不可避免地扩大整个交通系统的运营成本,并造成环境污染[1]。
为了减少无序的寻位停车造成的资源浪费,共享停车资源配置技术开始被大量研究[2-3]。开放式的居住区和智能车位锁的出现为共享停车奠定了基础,有研究表明适当调整预约停车和即到即停的比例可以有效降低停车系统的总成本[4]。共享停车系统的主体包括共享停车平台、车位供给者和停车用户。平台通过租赁车位供给者的车位空闲时段来出售给停车用户以获取利润,车位供给者需提前与平台交易车位空闲时段(车位供给)以取得利益,停车用户可以通过平台预约目的地附近的车位空闲时段(停车请求)以满足停车需求。
基于提前一天已知车位供给与停车请求的假设下,一些学者建立了共享车位预约与分配静态模型。Shao等[5]从平台角度建立了二元整数线性规划模型,进行停车资源分配。姚恩建等[6]提出了共享车位优化分配的改进图着色模型,利用蚁群算法进行求解。这两种方法与“先预约先服务”的分配方法相比,都使得车位利用率显著提高。孙会君等[7]从平台角度出发,对空闲车位租用和停车请求分配进行统一决策,提高了平台收入与停车周转率。
静态模型要求平台在获取全局停车信息后再统一分配车位。但是由于驾车出行的随机性较强,停车请求也会实时变化,所以相比于现有的静态模型,车位供给与停车请求的动态分配更加契合实际。因此,王韩麒[8]根据相似性算法建立了用户预约时段和车位共享时段的匹配度模型,该模型能够根据停车需求对分配方案动态优化。唐秋生等[9-10]提出了一种动态的居住区泊位“错时错位”共享停车方法,对车位拥有者“错位”调度,对停车用户“错时”共享。何胜学等[11]构建了无人驾驶条件下共享停车动态匹配模型,有效减少了无人驾驶车辆在泊车过程中不必要的频繁移位。
考虑到有限的车位难以满足高峰停车需求,在调节停车选择并提高停车效率方面,停车费价格优化和停车激励机制是灵活且可取的方式。Kotb 等[12]在车位分配模型中引入了动态定价机制,可根据车位利用率和预订数等定时更新停车价格,使平台利润最大化。郑士源等[13-14]建立了停车费的管理和优化模型,通过动态博弈分析了各因素对最优停车费和规模的影响。季彦婕等[15]基于博弈论建立了弹性停车激励机制来评估停车场的运营效益,激励机制不仅能保障停车场的可持续运营,还能促进车位的共享。Ottosson 等[16-17]计算了街道停车需求的价格弹性,探讨了定价对停车周转率、停车时间和总收入的影响。
现有研究的车位预约与共享多为静态模型[18-19],并基于提前已知所有的停车需求进行一次分配,未考虑停车需求的动态调整;且多数模型采用固定权重将不同目标进行线性组合,忽略了停车高低峰分配方案的差异性。因此,本文针对停车需求的分时段动态变化特征,提出分时段侧重不同目标,根据停车请求高低峰设置动态权重,综合考虑停车资源充分利用与用户停车成本最小化因素,构建多停车场动态预约与分配优化模型,实现停车需求的动态调整与分配。
1 车位动态预约与分配模型
1.1 问题描述
行政办公区和附近居住区的停车需求有明显的错峰性,这种错峰性提供了车位共享的条件[20]。假设在附近居住区有几个相邻的停车场,可整合为信息互通且资源共享的停车域。每个停车场有部分车位可以对外共享。每个共享车位在白天都有一定的可用时间窗,可提供给附近以行政办公和商业购物等为出行目的的停车用户。停车用户根据实际需求向平台提交停车请求,如果平台按照提交停车请求的顺序分配车位,可能会导致后面的停车请求不能满足,如果等所有请求提交完后再统一分配车位,这也不符合实际的动态停车需求。此外,由于需求的分时段动态变化特征,停车高峰与低峰应采取不同的策略进行分配。高峰时段保证更多的用户有位可停,从而减少因无效巡航而引发的拥堵;低峰时段则应侧重用户体验。除此之外,对停车场实施动态定价有利于实现停车资源的均衡利用。
因此,本文主要解决的问题是:能否根据实时的停车需求,引入动态权重与动态定价机制,建立多个相邻停车场共享车位的动态预约与分配模型,实现动态分配并对分配后的方案进行实时调整和优化。
1.2 模型思路与假设
本文提出了一个整数线性规划模型,将车位供给与停车请求进行动态分配,动态分配的关键在于平台将每天对外共享的时间划分为若干个时段,在每个时段中设置决策点并进行相应的分配决策。每次决策时,对于成功分配车位的停车用户,平台只会通知已成功预约目的地附近的车位,但是在到达预约的停车时间之前,平台可对其预约的车位进行不断调整来满足其他停车请求,当停车用户按照预约的停车时间到达目的地附近时,才会被告知预约车位的具体位置。从而实现在不影响停车用户条件下,通过调整已有分配来满足更多的停车请求。针对多停车场分配的特点,模型考虑了停车域内各个停车场间停车费率与停车后步行距离的差异,并考虑不同用户对停车费率与步行距离的敏感性的差异。
模型基于如下假设:
(1)假设多个相邻停车场都分布在目的地的最大可接受步行距离(800 m)范围内,且同一个停车场的车位没有差异;
(2)假设车位供给者和停车用户都会严格的遵守在平台所提交的共享时间,不会延时占用车位;
(3)假设停车用户根据分配的结果进行停车,不存在拒绝分配和私自更换车位的情况。
1.3 模型构建
平台每天根据车位供给者提供的时间窗,将对外共享的时间划分为多个时段(例如,每个时段30 min),令K为时段总数,k=1 为开始时段(例如8:00~8:30),k=K为结束时段(例如17:30~18:00)。i为决策时刻,I为决策的总次数,决策点位于每个时段的起始时间点(如8:00),则I=K。当时段划分足够小时,将近似模拟真实情况下的实时分配。令Z为停车域内相邻停车场的数量,Nz为停车场z的车位总数,停车域的车位数量为。D为停车域内目的地的总数。
M为第i次决策时停车域中的初始停车请求总数,为停车请求m的开始和结束时段。。当停车请求m在第i次决策时已预约成功但在第i+1 次决策时还未到,则记为待停车请求a,这些请求的总数记为A。模型涉及主要变量定义如表1所示。

表1 变量定义1)Table 1 Definition of variables
1.3.1 目标函数
(1)泊位利用时间最大
由于泊位资源的有限性,停车场方往往希望在满足用户需求的条件下能够最大程度的利用泊位资源,从而获取更多收入。因此,车场最优角度以泊位利用时间最大化为目标,其目标函数表示如下:
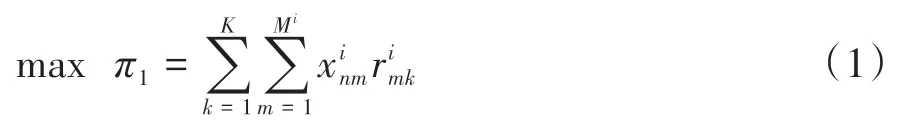
(2)用户成本最小
从用户利益出发,用户通常选择停车场时采用步行距离较短或低收费标准的原则。因此,采用用户停车价格与停车后步行距离来刻画用户停车成本,以用户停车成本最小化为目标,其目标函数表示如下:
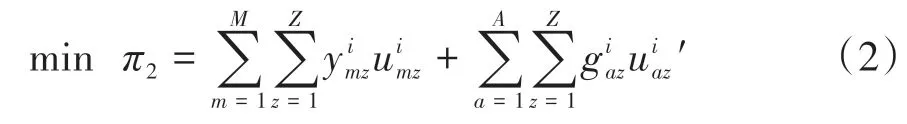
式中:等号右边第1 项表示第i次决策时,提交停车请求的M个用户的停车成本;第2 项表示第i次决策时,A个未到的待停车请求的停车成本。
(3)组合最优
为综合考虑用户与车场不同利益目标间的均衡,采用权重法,将上述两个目标进行组合。线性加权得到最终的目标函数如下:
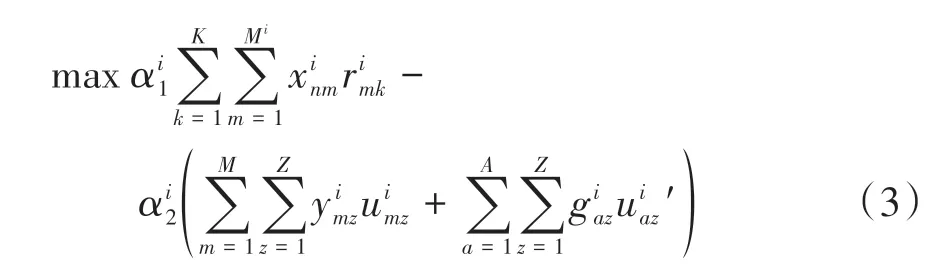
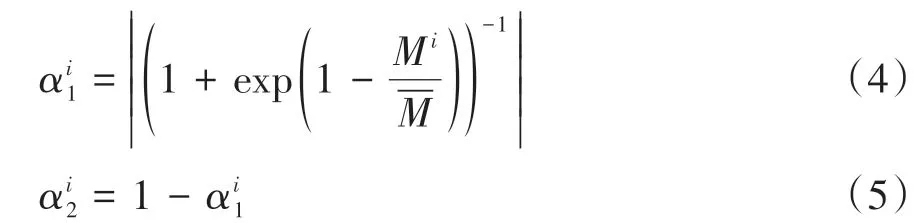
式中,Mi为第i次决策时提交的请求个数,为平均请求数,可由历史数据获取。由于Logistic 函数连续、光滑、严格单调递增,采用Logistic 函数将需求映射到[0,1]之间;当第i次决策时,有较多用户提交停车请求,即Mi大于时,取值介于0.5 与1 之间,目标函数倾向于停车资源利用最大化;当第i次决策提交停车请求的用户较少时,即Mi小于时,αi1 取值介于0 与0.5 之间,目标函数则倾向于使用户成本最小化;当停车请求接近均值时,取值约为0.5,则均衡考虑两个目标。
1.3.2 约束条件
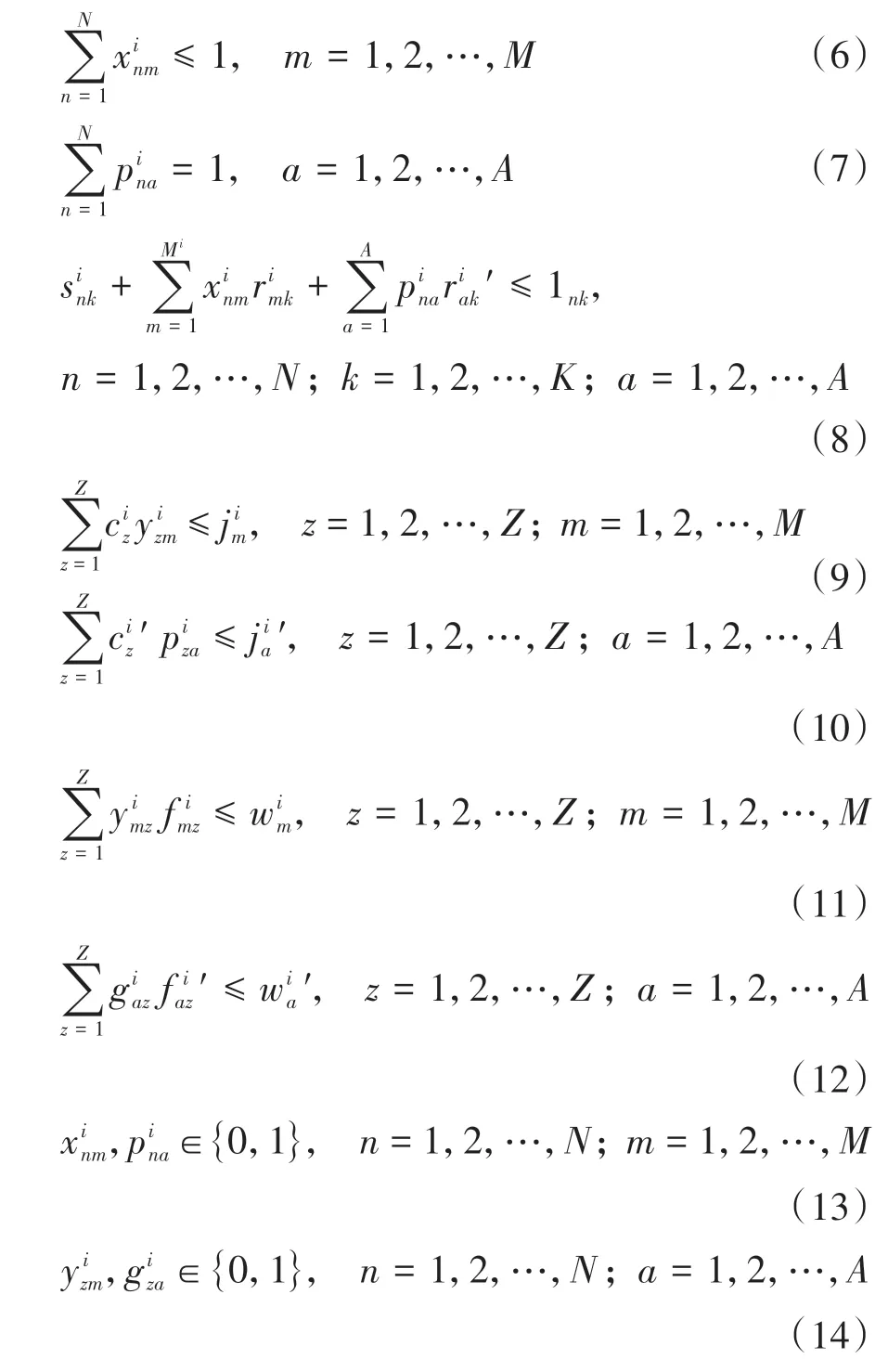
其中约束条件(6)表示将一个停车请求最多分配给一个车位;约束条件(7)保证要给待停车用户在新一轮决策中重新分配车位;约束条件(8)保证在每个时段内每个车位只能容纳一辆车。约束条件(9)、(10)分别表示每个停车请求与待停车请求分配到的车位对应的停车费用不能高于其最高可接受价格;约束条件(11)、(12)分别表示每个停车请求与待停车请求分配到的车位对应的停车步行距离不能高于其最高可接受步行距离。约束条件(13)、(14)表示是二进制变量。
1.4 动态模型决策与变量调整
本文所提出模型为0-1 整数线性规划模型,因此可以使用MATLAB(版本:2019 年)进行车位供给矩阵与停车请求矩阵的模拟生成,调用CPLEX(版本:12.8)求得问题(MILP)的最优解。
基于模型的求解,本文中通过调整待停车请求以实现停车资源的高效利用,动态分配流程具体步骤如下。
步骤1信息初始化,初始化决策时段数i=1,初始化Z个相邻停车场的车位供给矩阵整合Z个相邻停车场得到停车域的车位供给矩阵初始化车位分布矩阵BZ×N和停车域的步行距离矩阵LZ×D。
步骤2车场紧张度可以反映停车域中各车场的紧张程度,计算当前时段停车域的车场紧张度,并生成对应价格因子Vi,计算当前时段的停车费率;其中Cz表示停车场z单位时段的基础停车费。
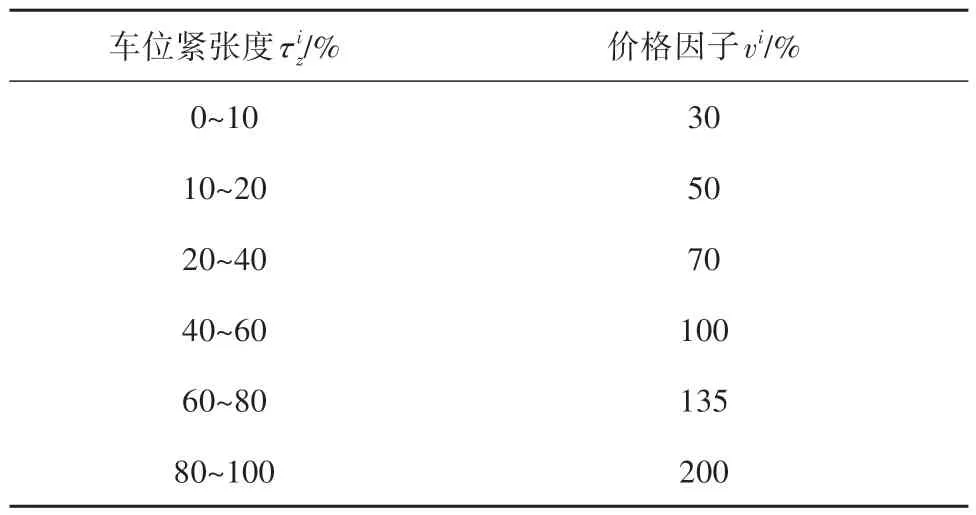
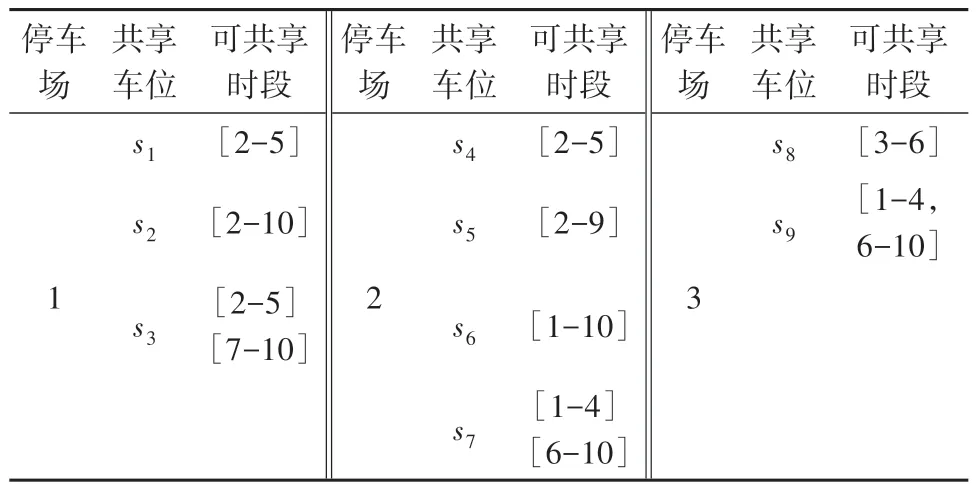
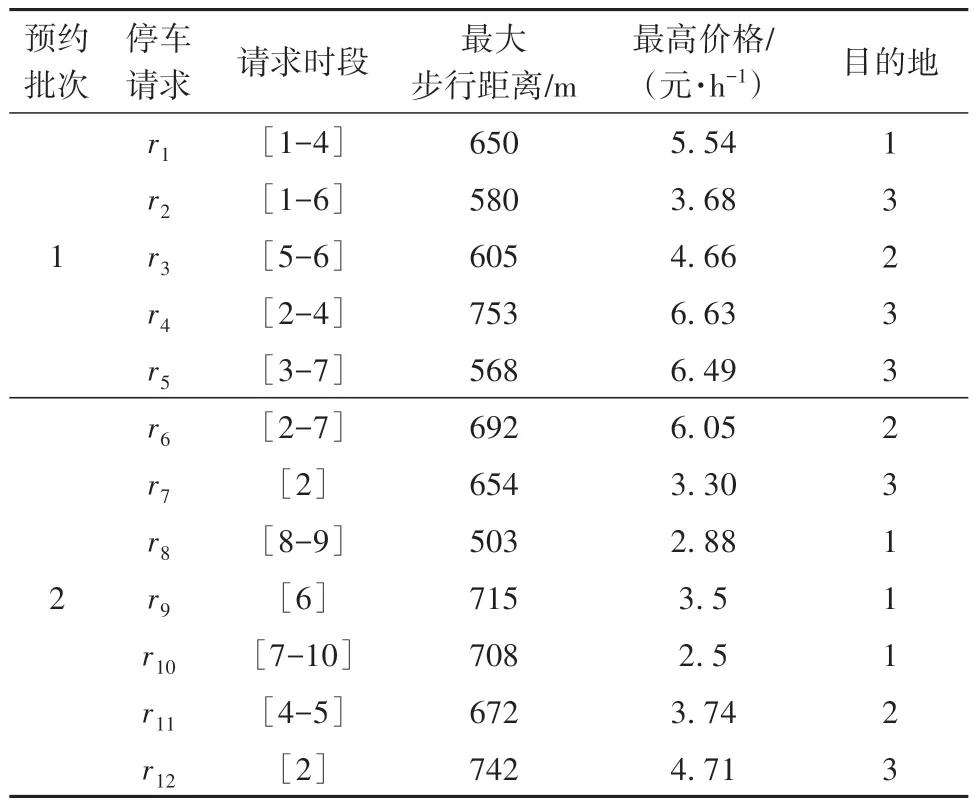
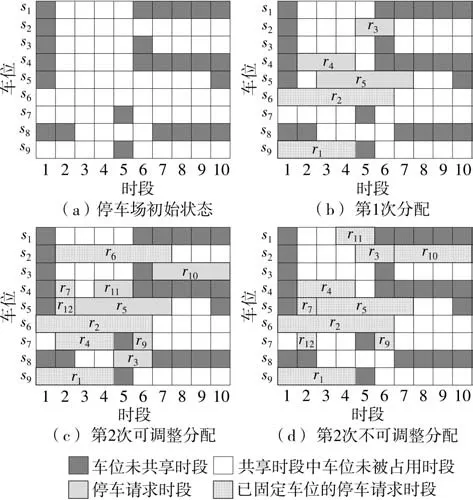
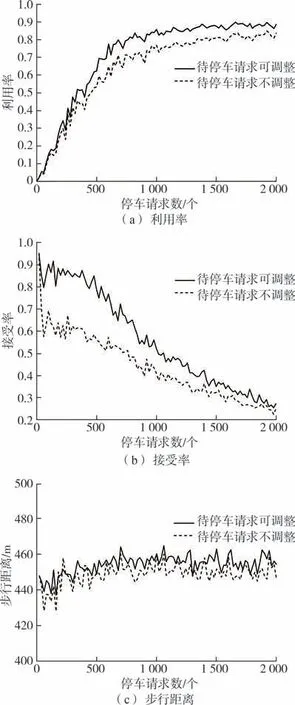
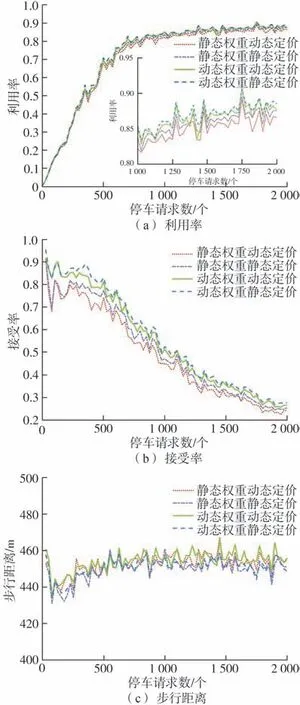
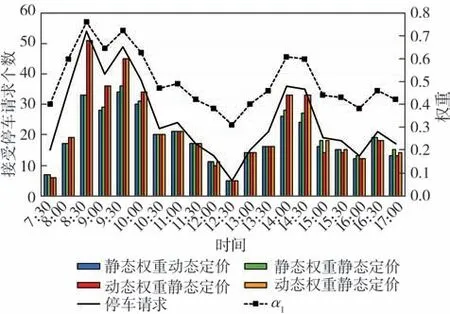
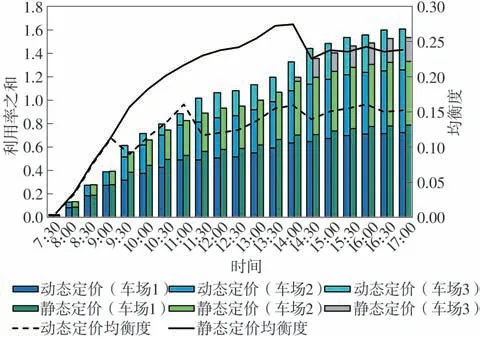
步骤7如果i 为了检验模型的有效性,采用车位利用率、停车请求接受率、平均步行距离和车场均衡度4个指标对模型进行评价。 车位利用率是指已占用停车时间与所供给的总停车时间之比。该指标可以反映共享车位是否得到充分利用,第i次决策时,停车场z的利用率可表示为 则停车域一天的最终利用率可表示为 停车请求接受率是指平台接受的停车请求数与停车用户发出的停车请求总数之比。当车位供给不能满足停车请求时,一些停车请求会被拒绝。停车请求接受率可以衡量平台的服务质量,第i次决策的接受率可表示为 则平台一天的停车请求接受率为 平均步行距离是指已成功预约车位的停车用户步行的距离除以这些停车用户的数量,平均步行距离大小可以反映停车用户的方便程度,可表示为 采用均衡度这一指标来刻画停车域内停车场的均衡利用情况,第i次决策,停车域的均衡度可表示为 为了验证所提出模型的有效性,设置仿真实验进行验证,仿真的基本条件如表2所示。 表2 仿真分析的基本条件Table 2 Basic information of simulation analysis 为平衡停车域内各停车场利用率与收入,减少交通拥堵,设定价格因子随着车位紧张度呈正相关指数增长,建立停车费率的动态定价机制如表3所示[12]。 表3 停车费动态定价机制Table 3 Dynamic pricing mechanism of parking fee 为了验证对待停车请求进行调整对分配效果的影响。本节设计算例与对比试验,将对待停车请求进行调整的模型(可调整模型)与基于当前停车需求进行分配的模型(不调整模型)进行对比。 2.2.1 算例 为了解释调整模型的机制,通过一个算例来进行说明。停车用户预约某一目的地附近3 个相邻的路外停车场。停车场1、停车场2 和停车场3距离目的地的距离及价格与仿真实验相同。各停车场有10 个共享时段,平台进行2 次分配。车位的供给时间窗如表4 所示,停车用户的请求信息如表5所示。 表4 共享车位可供给时段Table 4 Available period of shared parking slots 表5 停车请求信息Table 5 Information of parking requests 首先根据共享车位共享时段对车位进行描述,结果如图1(a)所示,对第一批次的5 个停车请求进行分配,分配结果如图1(b)所示。图1(c)与图1(d)分别代表第二次可调整与不调整的分配结果。 图1 调整与不调整模型的分配结果Fig.1 Allocation results of adjust and unadjusted models 可调整模型在第2次分配时可对未到达的待停车请求r3、r4、r5进行调整;可调整模型将对步行距离不敏感的停车请求r3由停车场1 调整至停车场3,从而使得停车请求r6被接受,不调整模型在第2 次分配时,由于没有合适的时间窗将停车请求r6拒绝。相较于不调整分配,可调整分配将待停车请求r4由车位s4调整至车位s7,使得停车请求r11由停车场1分配至停车场2,步行距离缩短。 2.2.2 模型对比 为了进一步验证模型的优越性,在仿真条件下对模型的评价指标进行了敏感性分析。一天的停车请求数从0 到2 000 变化。本文中将对比待停车请求的调整与不调整模型,对各评价指标随着停车请求的数量的变化进行分析,如图2所示。 在图2(a)中,可调整模型的停车域利用率ω显著高于不调整模型。调整待停车请求可使停车域利用率ω平均提升10.70%。可调整模型相较于不调整模型利用率的提升程度随着停车请求数量呈现先增大后减小的趋势。当停车请求较少时,可调整模型的优势并不明显,这是由于车位供给远大于停车需求,存在较多符合要求的可用车位,是否调整对停车域利用率ω影响不大;随着停车请求的增长,将部分对步行距离或泊位费率不敏感的待停车请求进行调整,从而使得平台接受更多停车请求,停车域利用率ω得到有效提升;当停车请求远大于停车供给时,各停车场达到饱和,无法通过调整使得利用率进一步提升,调整优势逐渐变小。 图2 停车场调整前后的评价指标对比Fig.2 Comparison of evaluation indexes before and after park⁃ing lot adjustment 在图2(b)中,相较于不调整模型,可调整模型使得平台接受率γ平均提升20.08%。当停车请求数小于400时,可调整模型的平台接受率稳定在0.85 左右,不调整模型的平台接受率稳定在0.63左右;当停车请求小于540时,平台接受率差值稳定在0.25 左右,后随着停车请求数量的增加,车位供不应求,两模型接受率差值逐渐缩小。 在图2(c)中,随着停车请求数的增加,可调整与不调整模型的用户平均步行距离均为450 m 左右,不调整模型相较与调整模型在步行距离方面存在略微优势,使得用户平均步行距离缩短10 m左右。由于模型约束条件的限制,每个用户所分配车位均小于其最大可接受步行距离,可调整模型虽然使得用户平均步行距离略微增大,但仍满足用户需求。 2.3.1 模型对比 为了进一步分析动态权重与动态定价的影响,将动静态权重与动静态价格的4 种组合进行了对比分析,结果如图3所示。 图3 动静态权重与动静态价格四种组合的对比Fig.3 Comparison of dynamic and static weight and dynamic and static price of four combinations 在图3 中,4 种模型对利用率与接受率的影响差别不大,其中动态权重模型相较于静态权重模型在利用率与接受率两个指标中有一定优势,利用率与接受率平均分别提升2.2%,10.88%。动态权重静态定价相较于动态权重动态定价在停车域内利用率与接受率两个指标中存在略微优势,利用率与接受率平均分别提升0.88%,2.93%。对于用户平均步行距离这一指标,4 种模型差异不大,均维持在450 m 左右。 2.3.2 动态权重效益讨论 由于上述4 种模型在总体的指标中差异不大,本节为进一步探究动态权重对分配结果的影响,为贴近一天中的实际停车需求分布,选取某一真实停车场的停车请求分布情况,利用模型进行分配,对结果进行对比分析,一天内各个时间段的分配情况如图4所示。 图4 各时段分配情况Fig.4 Allocation results of each period 由图4可知,上午8:00~10:00与下午14:00~14:30为停车请求的高峰时段。动态权重系数α1随停车请求数量同步变化。高峰时段动态权重模型的平均请求接受率为0.87,而静态权重模型的平均请求接受率为0.69。这是由于当停车需求较多时,动态权重模型倾向于停车资源利用最大化,优先考虑车位利用时间,从而使动态权重模型在停车高峰接受更多的停车请求,使得停车资源在高峰时段得到充分利用,避免了高峰期较多车辆因无法停车而无效巡航,进而引发交通拥堵。 2.3.3 动态定价效益讨论 在上述实验的基础上,为进一步验证动态定价因素对分配结果的影响,将动态权重动态定价模型与动态权重静态定价模型一天内各时段各车场的利用情况进行对比,结果如图5所示。 图5 各车场各时段利用情况Fig.5 Utilization of each parking lot in each time period 从均衡度这一指标来看,相较于静态定价模型,动态定价模型使得停车域均衡度平均降低0.074,说明动态定价模型使得停车域内停车资源利用更加均衡。从各车场各时段的利用情况可知,静态定价模型中车场1、2 的利用率显著高于车场3,这与停车费率有关,由于车场3 的停车费率高于车场1、2,模型为使得用户停车成本最小化,优先将用户分配至车场1 与车场2,导致停车域内分配不平衡。而动态定价模型根据车场的利用情况对价格进行调整,使得车辆均匀的分配至各车场,平衡停车域内各停车场利用率,进而减少交通拥堵。 本文从共享停车平台和停车用户的角度出发,提出了更加符合实际的多个停车场共享车位动态预约与分配优化模型。该模型在时间窗与用户偏好的约束下,引入了动态定价机制,根据停车请求高低峰设置动态权重,侧重不同目标,并对已分配方案不断优化和调整。然后对比分析调整优化、动态价格与动态权重对分配结果的影响。结果表明本文中提出的模型不仅满足了更多的停车请求,还使得车位供给充分利用。此外,动态权重能够更好的适应需求的波动性变化。停车场实施动态定价有利于停车资源的均衡利用。 在将来的研究中,还需要考虑车位被延时占用后的分配情况以及异质停车场车位供给者受租赁价格的影响;同时考虑将模型应用于实际,对模型的普适性进行验证。1.5 模型效果评价指标

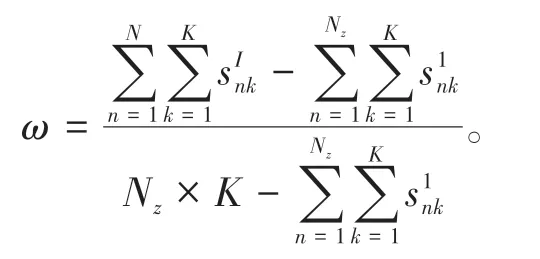

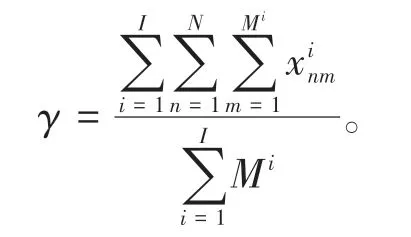
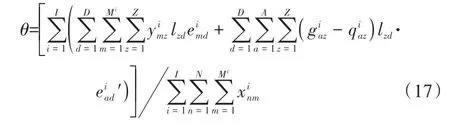

2 数值实验
2.1 仿真条件

2.2 调整效益分析
2.3 动态权重与动态定价效益讨论
3 结语
