微粒子喷丸齿轮法向接触刚度模型
2022-11-20莫海军赵航成雨黄杰陈思宏柯韦圣万珍平
莫海军 赵航 成雨 黄杰 陈思宏 柯韦圣 万珍平†
(1.华南理工大学机械与汽车工程学院,广东广州 510640;2.珠海市钧兴机电有限公司,广东珠海 519170)
随着新能源汽车齿轮箱向着高转速、高效率、长寿命、低噪音方向发展,齿轮制造技术也由高精度制造向高性能制造方向转变[1-2]。喷丸强化技术由于工艺简单、提高零件疲劳寿命效果显著、成本低等特点,成为齿轮加工制造的关键技术之一[3]。传统喷丸因采用较大的弹丸直径,导致喷丸强化后的齿轮表面粗糙度以及齿面变形增大,无法满足高精度、高性能齿轮的制造要求。微粒子喷丸因弹丸粒径在0.02~0.10 mm之间,喷丸速度大于150 m/s,具有变形小以及降低零件表面粗糙度等优点[4],因此微粒子喷丸强化技术已成为高性能齿轮制造的重要方法之一[5]。
近年来,国内外研究人员对微粒子喷丸强化机理及应用进行了大量研究,但主要集中研究分析齿轮喷丸强化效果以及喷丸工艺参数对齿轮疲劳寿命的影响,并且大多以实验为主。一般情况下,微粒子喷丸强化可以使齿轮的疲劳寿命提高30%以上[6-8]。然而,对微粒子喷丸前后齿面微观形貌表征以及齿轮动态接触特性影响的研究较少。高速齿轮系统动力学研究中,法向接触刚度作为齿轮动态接触特性的重要部分,精确建立微粒子喷丸齿面法向接触刚度模型,对提高齿轮动力学性能以及进一步分析微粒子喷丸对高性能齿轮的影响具有重要意义。
Majumdar等[9]基于分形理论首次建立了结合面接触特性模型(M-B模型),并仿真分析了微观形貌参数对模型的影响规律。许多学者基于M-B 模型,进一步研究齿轮的接触特性。王晓鹏等[10]运用分形理论建立微点蚀齿轮法向接触刚度模型,研究发生不同程度微点蚀的齿轮法向接触刚度特性。刘鹏等[11]通过引入摩擦因素推导出适用于微线段齿轮的法向接触刚度模型。Wu 等[12]建立了考虑摩擦因素及弹塑性变形的渐开线圆弧齿轮法向接触刚度模型。李小彭等[13]运用分形理论描述齿轮轮廓并分析不同分形维数D下的齿轮啮合刚度对齿轮系统动力学特性的影响。
综上所述,许多学者针对不同工况或者不同齿形齿轮的接触特性进行相关研究,但大多都基于基础的分形理论对齿面进行形貌表征,构建齿轮接触特性模型,而未针对齿面形貌考虑微凸体相互作用、弹塑性变形等影响因素。微粒子喷丸后齿面会发生一定程度的弹塑性及塑性变形,且形成微米甚至纳米级的凹坑,因此在微粒子喷丸齿轮实际啮合过程中,微凸体间的接触会产生相互作用以及弹塑性变形。
为更加精确地分析微粒子喷丸齿轮法向接触刚度特性,文中对微粒子喷丸齿面微观形貌进行分析,基于分形理论,结合齿轮真实啮合过程,考虑微凸体相互作用及微凸体弹塑性变形对接触特性的影响,构建微粒子喷丸齿轮表面法向接触刚度模型,定量研究喷丸前后及不同喷丸参数对齿轮法向接触刚度的影响,进一步改进和完善齿轮动力学齿轮啮合刚度计算数学/力学模型。
1 微粒子喷丸齿面形貌分析
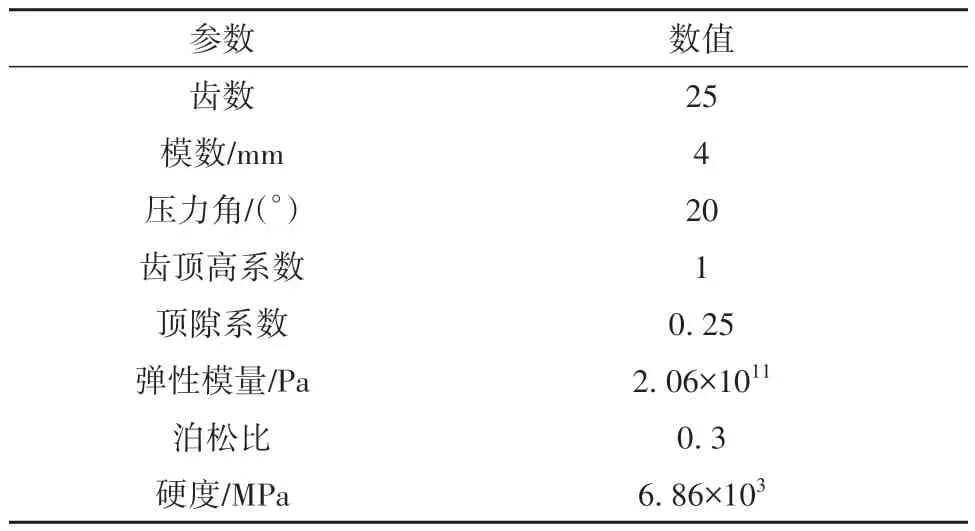
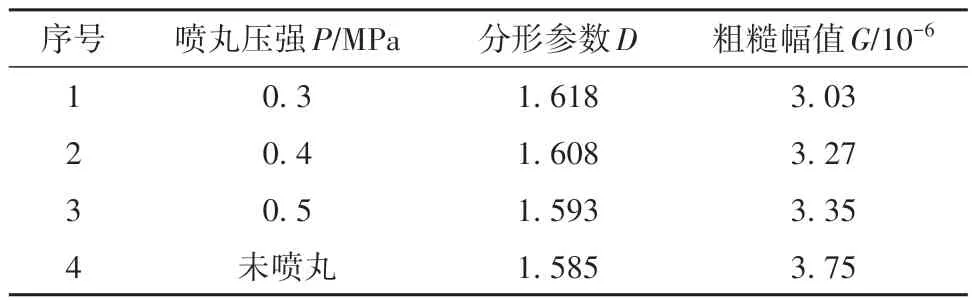
文中采用材料为20CrMo 的渐开线齿轮作为微粒子喷丸对象,喷丸参数如表1所示。使用Mitutoyo粗糙度仪测其表面粗糙度,图1为四组齿轮表面粗糙度值,由图可知,微粒子喷丸齿轮表面粗糙度值低于未喷丸齿轮,其次,随着喷丸压强的增大,齿轮表面粗糙度值也随之增大。
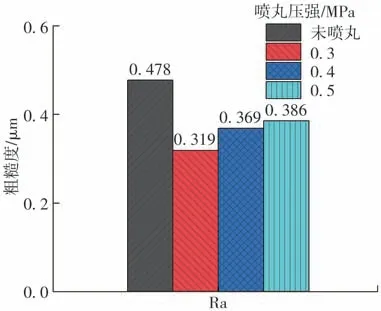
图1 不同喷丸参数齿轮表面粗糙度Fig.1 Surface roughness of gears with different shot peening parameters

表1 喷丸参数Table 1 Shot peening parameters
采用Quanta 200 环境扫描电子显微镜观察分析微粒子喷丸前后齿面的表面形貌,如图2(a)、2(b)所示。未喷丸表面存在许多平行的磨痕,为明显的磨削加工痕迹。微粒子喷丸表面形貌整体呈现为叠浪型,且表面呈现微米甚至纳米级弹坑,表面形貌更加均匀,微凸体尺度更小,因此微粒子喷丸后表面粗糙度值小于未喷丸齿轮表面,可将微粒子喷丸齿面视为随机分布着无数个微凸体。

图2 微粒子喷丸前后齿面形貌图Fig.2 Surface topography before and after fine particle shot peening
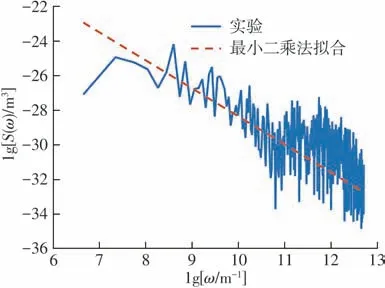
通过对微粒子喷丸齿面微凸体的分布及接触特性分析,推导微粒子喷丸齿面的分形接触参数,从而建立微粒子喷丸齿面接触刚度模型。为能够更加准确表征实际齿面形貌特征及提取相关特征参数,文中对微粒子喷丸齿轮齿面形貌的高度数据进行提取,图3(a)、3(b)为采用Olympus OLS 5000-SAF激光共聚焦显微镜对齿面形貌高度信息的采集结果。根据齿面高度信息,后文将采用功率谱密度函数法计算得出齿轮微观分形参数。
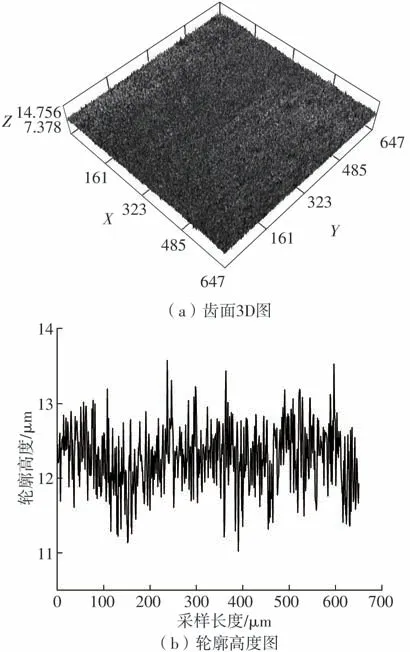
图3 微粒子喷丸齿轮高度信息Fig.3 Height information of fine particle shot peening gears
2 考虑微凸体相互作用的分形接触模型
2.1 单个微凸体分形接触模型
为了表征具有无序、随机分布微凸体的微粒子喷丸齿面,进而分析齿轮法向接触刚度,文中运用Weierstrass-Mandelbrot 分形函数[14](W-M 函数)表征具有无序、随机等行为的微粒子喷丸齿面,表达式如下:
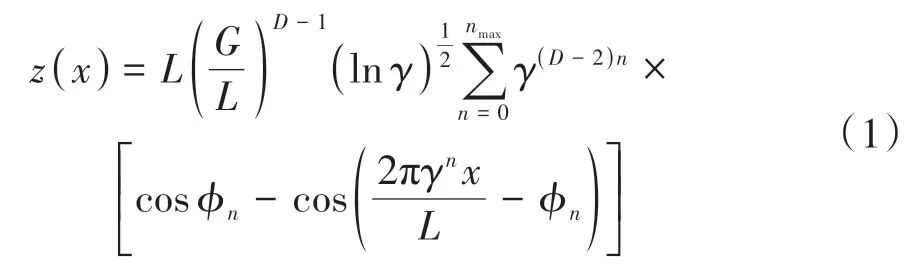
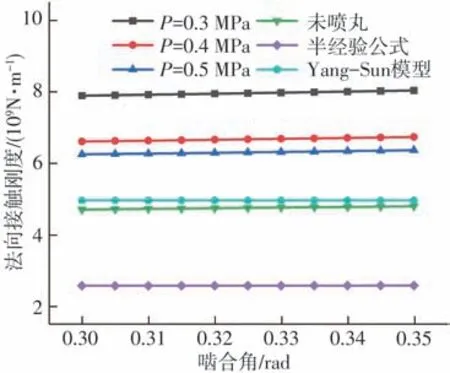
式中:z为轮廓高度;G为分形粗糙度幅值;D(1 将两粗糙接触表面等效简化为一粗糙表面和一刚性光滑平面接触,单个微凸体与刚性光滑平面接触如图4所示。其中δ为微凸体的变形量,r为微凸体真实接触面积的半径,r'为微凸体的截断接触面积的半径,R为微凸体的峰顶曲率半径。 图4 微凸体接触示意图Fig.4 Contact diagram of asperity 根据式(1),加载后单个微凸体的变形量δ等于余弦函数的峰谷幅度差,即当cosϕn=1 和时,单个微凸体的变形量δ如下: 式中,a'为微凸体的截断接触面积,a'=πr'2。 由图4的几何关系可知,微凸体的峰顶曲率半径R为 为了确定微凸体的分形接触参数,必须对单个微凸体的接触状态进行研究,即微凸体的三种变形状态:弹性变形、弹塑性变形和完全塑性变形[15-16]。 2.2.1 弹性变形阶段 Wang等[17]基于弹性理论和Hertz接触理论建立了考虑微凸体相互作用的结合面力学模型,推导出弹性变形状态下微凸体的接触载荷表达式: 式中,ae为微凸体的实际接触面积,ae=πr2;E为两接触面材料的综合弹性模量[17],其表达式为 式中:E1、E2、γ1、γ2分别是两粗糙表面的弹性模量和泊松比。 根据圆形弹性微接触[18],微凸体在弹性变形状态下的实际接触面积ae可表示为 将式(3)和式(6)代入式(4)可得到弹性变形状态下微凸体的接触载荷fe与截断接触面积a'的函数关系式: 则单一微凸体接触刚度的表达式为 当微凸体刚发生屈服时,微凸体临界接触载荷fec表达式[17]为 式中,σy为较软材料的屈服强度;aec为临界接触面积。 由式(7)和(9)可得刚发生屈服时的临界截断接触面积和临界接触弹性变形量δec。 2.2.2 弹塑性变形阶段 2002 年Kogut 等[19]建立了可变形球被刚性平面压扁后的有限元接触模型,分析了变形量增大时弹塑性接触界面的演化过程,该模型提供了接触载荷、接触面积的无量纲表达式: 式中,fep、aep分别为微凸体弹塑性状态下的接触载荷、实际接触面积。 由式(4)、(10)、(13)、(14)得: 当δ=6δec时,第一弹塑性临界截断接触面积可联立式(12)得: 2.2.3 完全塑性变形阶段 当δ≥110δec时,微凸体发生完全塑性变形,临界完全塑性变形量[16]表达式为: 将式(18)带入(12),得到微凸体临界完全塑性变形截断接触面积: 完全塑性变形阶段,其接触载荷和接触面积[16]表达式为 由文献[20]可知,平面接触面积分布函数n1(a')表达式如下: 式中:ψ为区域扩展系数;a'l为最大微凸体的截断接触面积;ψ与分形维数之间的关系[21]为: 由于齿轮齿面接触微凸体接触个数与平面微凸体接触不同,陈奇[22]将两曲面接触等效为两圆柱体接触,给出圆柱面接触系数λC表达式: 式中:B为圆柱体宽度;R1、R2为对应的圆柱体曲率半径。则齿面接触微凸体的面积分布函数n(a')为 两接触表面真实接触面积是所有接触微凸体接触面积总和[23],表达式为 式中:Are、Arep1、Arep2、Arp分别为弹性接触面积、第一弹塑性接触面积、第二弹塑性接触面积和塑性接触面积。 两接触表面总的接触载荷是所有接触微凸体接触载荷的总和[23],表达式为 式中:Fne、Fnep1、Fnep2、Fnp分别为弹性接触载荷、第一弹塑性接触载荷、第二弹塑性接触载荷和塑性接触载荷。 王润琼等[24]研究表明微凸体在弹性变形阶段表现出刚度特性,而在塑性变形阶段微凸体并不会表现出刚度特性。所以两接触表面总的法向接触刚度是表面所有接触微凸体发生弹性变形表现的接触刚度之和,表达式为 将式(28)、式(29)进行无量纲化,得到量纲一的法向载荷、法向接触刚度计算模型: 式中,Aa为名义接触面积。 图5(G=10-11,λC=0.7)为法向接触刚度随法向载荷以及分形维数D的变化规律,可以看出,量纲一的法向接触刚度Kn*随着量纲一法向总载荷Fn*的增大而增大,即法向载荷增大时,圆柱接触面法向接触刚度也随着增加。此外,量纲一的法向接触刚度随着分形维数D的增大而增大。 图5 分形维数对法向接触刚度的影响Fig.5 Influence of fractal dimension on normal contact stiff⁃ness 图6(D=1.6,λC=0.7)为法向接触刚度随法向载荷以及分形粗糙幅值G的变化规律。可以看出,法向接触刚度随分形粗糙幅值的增大而减小。 图6 分形粗糙幅值对法向接触刚度的影响Fig.6 Influence of fractal roughness amplitude on normal contact stiffness 图7(D=1.6,G=10-11,λC=0.7)为法向接触刚度随法向载荷以及材料特性参数的变化规律,可以看出,量纲一的法向接触刚度Kn*随材料特性参数的增大而增大,即提高材料屈服强度可以提高法向接触刚度,进而提高接触表面承载能力以及抵抗变形的能力。 图7 材料特性参数对法向接触刚度的影响Fig.7 Influence of material characteristic parameter on normal contact stiffness 通过对分形接触模型仿真分析可知,分形参数D和G对法向接触刚度的影响具有一致性,即增大分形维数和提高表面光洁度能增大表面法向接触刚度;从而提高接触表面抵抗变形的能力。 分形参数是由W-M 函数的功率谱函数与波长的对数曲线确定的,根据文献[25]得到微观形态的功率谱密度函数如下: 功率谱密度函数两边同时取对数,得: 令k=2D-5,c=2(D-1)lgG-lg(2lnγ),则式(32)可以表示为 如方程式(34)所示,在双对数坐标系下微观形态的功率谱密度函数是一条直线,通过斜率和纵坐标截距求得分形参数D和G: 前文对粗糙表面的轮廓高度信息进行测量,得到离散的轮廓高度数据z(x),如图3(b)所示。将测量的离散数据进行快速傅里叶变换(FFT)并取双对数,得到测量轮廓的对数功率谱密度函数lgS(ω),再对其进行最小二乘法的一次多项式拟合,得到如图8所示的功率谱图。 图8 功率谱图Fig.8 Graph of power spectrum 本文采用材料为20CrMo 的渐开线齿轮作为微粒子喷丸对象,渐开线齿轮副相关计算参数如表2所示。 表2 渐开线齿轮副相关计算参数Table2 Relevant calculation parameters of involute gear pair 由Bobillier 法则作图法[26]和齿轮齿廓相关计算参数,得出齿面上啮合点的曲率半径与啮合角的关系[27]: 式中:m为模数;α为压力角;z1、z2为主从动轮齿数;α1m、α2m为主从动轮啮合点啮合角;ρ1m、ρ2m为主从动轮啮合点曲率半径。 由两圆柱体Hertz 接触理论推导出接触半宽与啮合角的关系[27]: 式中,F为载荷,P为输入功率,n为转速,R1m为主动轮啮合点半径,B为齿宽,b为接触半宽。 由前文分形参数提取方法对不同微粒子喷丸参数齿轮进行计算,得到不同喷丸参数齿轮表面的分形参数D和G如表3所示。 表3 不同喷丸参数齿轮的分形参数Table 3 Fractal parameters of gears with different shot peening parameters 由表3可知,随着喷丸压强的增大,分形维数减小,粗糙幅值增大,其变化趋势与齿面粗糙度变化一致,即表面粗糙度增加,表面光洁度降低,分形越粗糙。因此分形参数提取结果可信。 将各计算参数代入法向接触刚度模型进行仿真计算,并与Yang-Sun模型[28]和NASA报告中的半经验公式[29]对比,结果如图9所示。由图可知,微粒子喷丸齿轮法向接触刚度大于未喷丸齿轮法向接触刚度,即微粒子喷丸可以提高齿轮法向接触刚度;其次,随喷丸压强的增大,齿轮法向接触刚度呈现出减小的趋势,因此合理的调控微粒子喷丸参数是提高齿轮接触刚度,进而增强齿轮接触疲劳强度的关键。 图9 不同喷丸效果的齿轮法向接触刚度Fig.9 Normal contact stiffness of gears with different fine par⁃ticle shot peening effects 通过与两种刚度模型的对比可知,本文中提出的模型与两种对比模型的法向接触刚度数量级均在109,体现出本文模型的正确性。由于Yang-Sun模型和NASA 报告中的半经验公式两种刚度模型都未考虑接触表面微观形貌特征,仅从齿轮宏观几何尺寸角度分析齿轮刚度特性,因此在具体数值上本文模型与两种对比模型存在差异。由文中模型分析结果可知:微粒子喷丸在一定程度上影响齿轮法向接触刚度,可见对于分析高性能齿轮的接触特性,不仅需要考虑齿轮宏观几何尺寸,还应对齿面微观形貌特性进行分析,从而更加准确地分析齿轮接触特性。 (1)从微观层面对比分析了微粒子喷丸前后齿轮表面形貌的变化。结果表明,微粒子喷丸使得齿面发生变形,形成随机的微米级甚至纳米级凹坑,且微粒子喷丸齿轮表面粗糙度低于未喷丸齿轮表面粗糙度。 (2)建立了考虑弹性-弹塑性-塑性变形以及微凸体相互作用的齿轮结合面法向接触刚度模型,得到分形参数对法向接触刚度的影响规律。法向接触刚度随分形维数的增大而增大,随粗糙幅值的增大而减小。 (3)分析了微粒子喷丸前后及不同喷丸强度对齿轮法向接触刚度的影响规律。相较于未喷丸齿轮,微粒子喷丸能提高齿轮法向接触刚度,随着喷丸强度的提升,齿轮法向接触刚度降低。 综上所述,微粒子喷丸工艺不仅在提升齿轮疲劳寿命及控制变形方面有独特的优势,而且对齿轮接触刚度的提升也具有一定的效果。本文也为后续齿轮系统动力学及微粒子喷丸工艺等的进一步研究做了铺垫。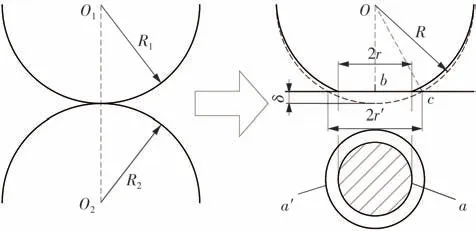


2.2 单个微凸体接触状态分析
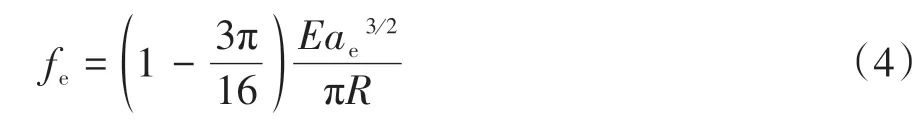
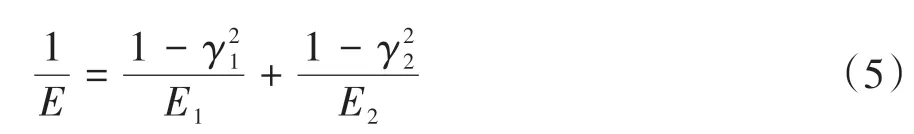

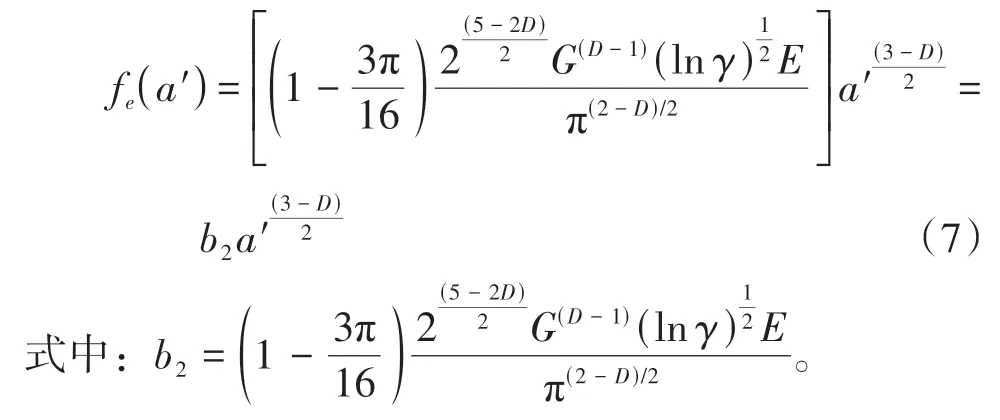
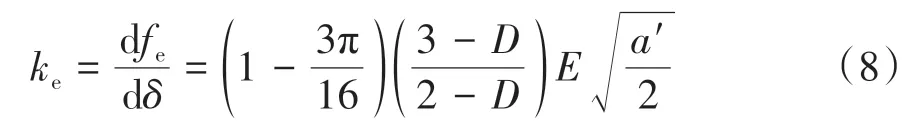


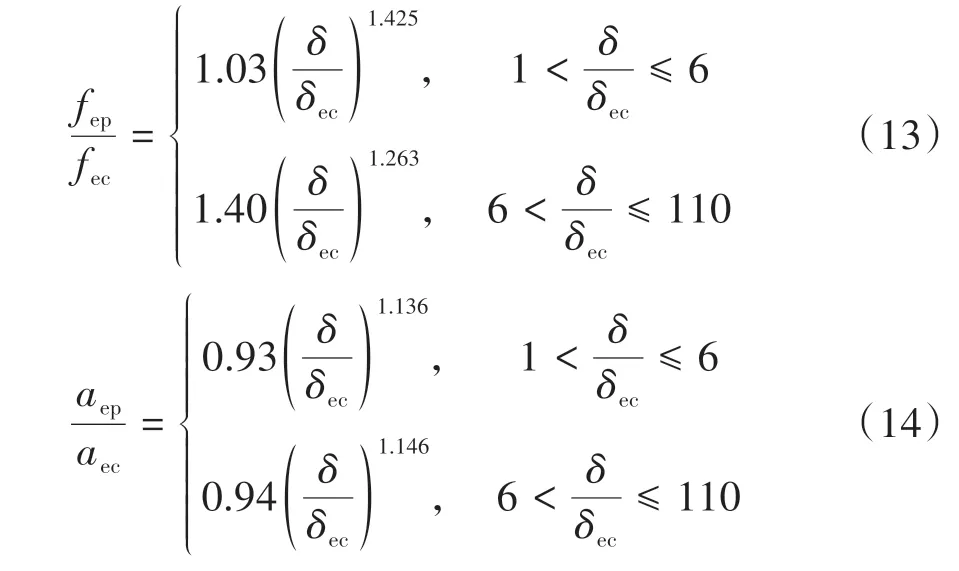
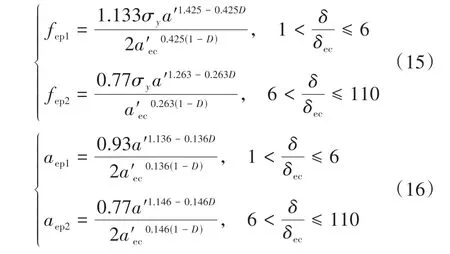




2.3 法向接触刚度模型

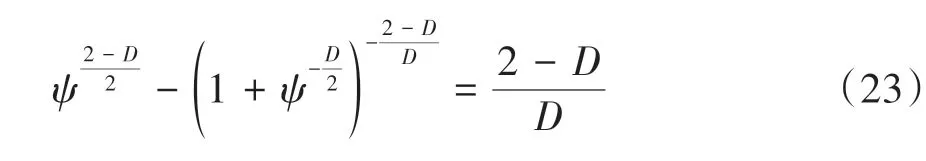

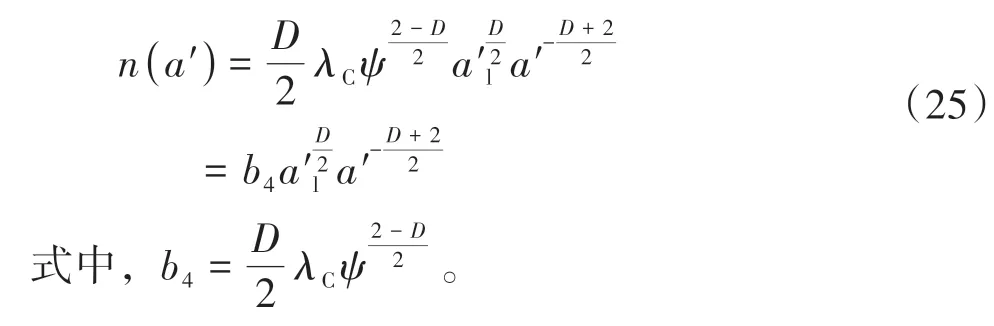


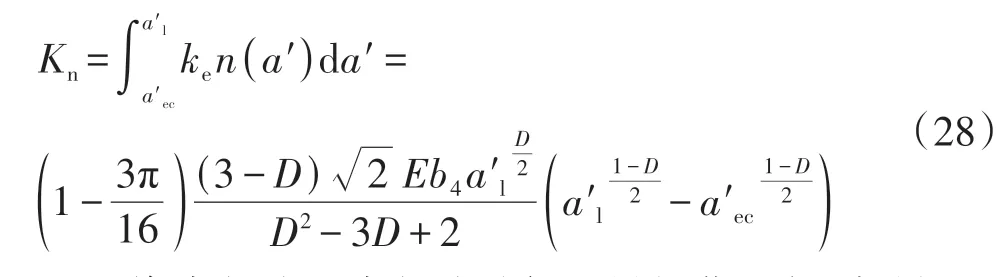

2.4 分形接触模型仿真分析
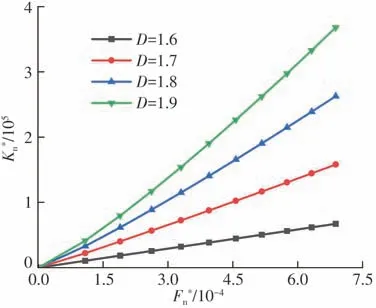

3 微粒子喷丸齿面法向接触刚度
3.1 分形参数的提取

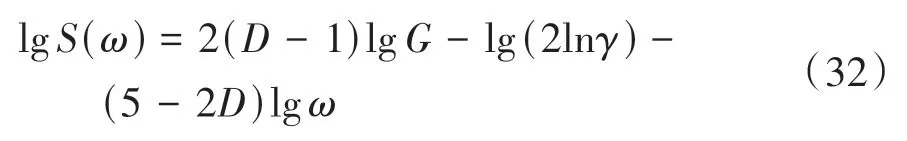

3.2 微粒子喷丸齿轮法向接触刚度分析
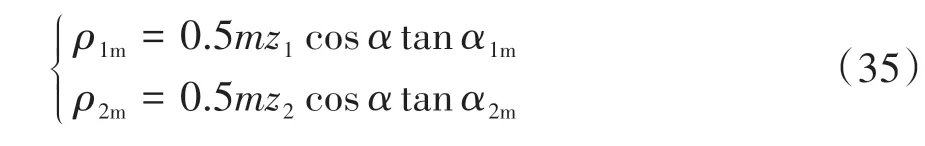

4 结论
