基于膨胀图卷积与离群点过滤的残缺点云配准
2022-11-20孙战里张玉欣
孙战里,张玉欣,陈 霞
1.安徽大学 人工智能学院,合肥 230601
2.安徽大学 多模态认知计算安徽省重点实验室,合肥 230601
3.安徽大学 电气工程与自动化学院,合肥 230601
4.安徽农业大学 信息与计算机学院,合肥 230036
点云配准是一项通过计算刚性转换参数将两个点云进行对齐的研究任务。在实际应用中,由于扫描设备等一些原因,多数情况下所获得的点云并不是完整的,或许会存在残缺,对于残缺点云进行配准的研究是必要的。与完整点云配准相比,残缺点云的配准通过检测源点云与目标点云的稀疏关键点来计算两个点云的对应关系。残缺点云配准作为一项计算机视觉中的重要任务,被广泛应用于许多应用中,如自动驾驶汽车[1]、医学图像[2]和3D图形表示[3]等。
近年来,点云配准任务的算法通过使用视觉、图形和优化机制得到了稳步改进。ICP(iterative closest point)[4]作为早期算法,由于其简单性以及计算复杂度较低等优点,成为配准任务当中最经典的方法。然而,ICP可能会陷入局部最优,且遇到异常值时其配准能力会显著下降。为了缓解这些问题,许多算法对ICP进行了优化。文献[5-6]提出将概率的方法应用到ICP当中,处理配准当中的不确定性。文献[7-8]提出全局配准模型,缓解产生的局部最优问题。文献[9]将Levenberg-Marquardt算法应用到ICP目标中,提高了模型的鲁棒性。文献[10]将DNT(normal distribution transform)与ICP相结合对点云位姿进行精确的估计。然而,这些方法通常比经典的ICP慢几个数量级,并且有些方法具有必须逐个调整的超参数。因此,这些传统算法难以达到效率与效益的平衡,实用性不高。
随着深度学习的火热与快速发展,基于卷积神经网络的配准算法取得了突破性的进步。这些算法显示,即使在不同的数据集上,基于深度学习的配准算法不论是速度还是鲁棒性上都优于传统算法。文献[11]提出了PointNetLK,该模型将PointNet[12]与Lucas & Kanade算法[13]整合到网络中来处理完整的点云,提高了点云的置换不变性。但是由于点云存在无序性等问题,对于点云特征的有效提取成为点云配准当中至关重要的一步。文献[14]提出DCP(deep closest point)模型,代替PointNet,该模型采用动态图卷积网络(dynamic graph convolutional neural network,DGCNN)[15]对点云进行特征提取,这种提取方式将动态边缘卷积的思想应用到点云中,很大程度缓解了输入点云无序性的问题。此外,使用奇异值分解[16]来获取转换参数。值得注意的是,PointNetLK与DCP只适用于处理完整的点云,并不适用于处理残缺点云。因此,一些网络被提出解决此问题。PRNet[17]在DCP的基础上,通过使用关键点检测模块与Gumbel-Softmax[18]处理点云配准问题。IDAM(iterative distance-aware similarity matrix convolution network)[19]通过融合几何特征与点对之间的欧几里德偏移学习匹配点,克服了简单取特征向量内积进行匹配的缺点。此外,FMR(feature-metric registration)[20]利用最小化源点云与目标点云之间的对齐误差(如倒角距离)来学习转换参数进行配准。文献[21]将修改后的LPDNet与注意力机制整合到一起解决残缺点云配准任务。然而,现存的基于学习的方法提取到的特征并不能细节地表示点云,而且离群点对于残缺点云的影响也没有被考虑到,这些对于提高点云配准精度是至关重要的。
为了解决上述问题,本文设计了一个基于深度学习的残缺点云配准网络。该网络主要包含膨胀图卷积块、密集连接与离群点过滤模块三部分。首先,借鉴膨胀卷积的思想,将其应用到图卷积中构成膨胀图卷积块。该块通过逐步增加膨胀率,使得网络在不降低分辨率的同时逐渐增加对于点云的感受野,增强网络学习点云几何表示的能力。其次,对于膨胀图卷积块的输出,使用密集连接形式对这些输出执行跳层连接,融合不同层输出的特征,进一步增强特征表示能力。将密集连接与膨胀图卷积构成的模块称为密集膨胀图卷积模块。最后,构造了一个基于深度网络与标准化相结合的离群点过滤模块。该模块将点对应关系看作一个分类问题,通过对点对进行标准化进而输出对应的权重来过滤掉不匹配的点对。此外,对于所获得的权重,使用它来对配准模型进行加权增强模型的鲁棒性。
1 模型介绍
本文将首先描述关于点云配准问题的预备知识,然后再分别介绍密集膨胀图卷积模块、关键点检测模块、离群点过滤模块和奇异值分解模块,最后介绍网络所使用的损失函数。
1.1 点云配准方法描述
记源点云为X={xi∈ℝ3|i=1,2,…,N},目标点云为Y={yj∈ℝ3|j=1,2,…,M},其中N与M分别代表X与Y的个数,xi与yj分别代表X与Y中第i与第j个点的特征向量,ℝ3代表原始点云的特征维度为3维。点云配准的任务就是通过计算两个点云之间的最优转换参数(旋转矩阵R∈SO(3)与平移向量t∈ℝ3)配准两个点云[17]:
其中,ym(xi)是点xi在目标点云Y中对应的点。
本文提出的整体网络结构如图1所示。首先,对于X与Y,使用密集膨胀图卷积模块提取丰富的细粒度特征。然后,将X与Y的高维特征与原始三维特征分别输入到关键点检测模块[17]中获得P个关键点。之后,利用所获得的X与Y各自的P个关键点,使用离群点过滤模块计算它们之间的对应关系权重。最后,将权重输入到奇异值分解模块获得所需要的转换参数。至此,完成了一次迭代,获得最优转换参数需要将图1所示网络进行n次迭代。每次迭代转换参数之间的关系可以用下列公式表示:
每经过一次迭代,源点云就会进行一次位姿转换:
1.2 密集膨胀图卷积模块
密集膨胀图卷积模块如图2所示,其由4个膨胀图卷积块(dilated graph convolution block,DGCB)组成,并使用密集连接(DenseNet,DN)将DGCB得到的特征进行跳层连接。
1.2.1 膨胀图卷积块
DGCB如图3所示。源点云X与目标点云Y都要经过DGCB模块进行特征提取,因此以X为例介绍DGCB流程。对于每一个DGCB,首先对输入点云利用膨胀KNN[22]构建图G={V,E},其中V表示N个顶点的特征集合,记为V={xi∈ℝdin|i=1,2,…,N},din表示输入维度,每层DGCB的输入维度分别为3、64、64、64。E={Ei∈ℝk×din|i=1,2,…,N}表示边特征集合,其中Ei={eij∈ℝdin|j=1,2,…,k}代表每个点的边特征集合,k代表选取的近邻点的个数。每个点的第k个边可以表示为:
其中,xik为点xi利用欧氏距离寻找出的第k个近邻点。与普通KNN不同,如果要使用顶点与k个近邻点构建图的话,膨胀KNN要先找寻k×r个近邻点(xi1,xi2,…,xi(k×r)),r为膨胀率。为了逐渐增加感受野,设置每层r的值分别为1、2、3、4。寻找k×r个近邻点后,再每隔r个点选取一个构图所需要的点,选取的点可以表示为(xi1,xi(1+r),…,xi(1+(k-1)×r))。
图4 可视化了膨胀KNN(r=2)与普通KNN的区别。经过膨胀KNN后,点xi的局部邻域图特征ji可以用下列公式表示:
其中Conv(·)代表1×1卷积层,maxpool(·)代表最大池化,gi的输出维度为dout,每层DGCB的dout均为64。
1.2.2 密集连接
为了加强特征的传递,更有效地利用特征,使用了密集连接[23]对膨胀图卷积的输出进行融合。l表示点xi经过DGCB的层数(本文设置层数l为4),第l+1层的输出可以表示为:
其中,Gl代表经过第l层的特征输出,dl(·)代表第l层
DGCB。
最终,将每层DGCB的输出进行级联操作并且经过1×1卷积得到密集膨胀图卷积模块的输出Gzong:
其中,Gzong的维度为N×512。
1.3 关键点检测模块
为了将不同点数的两个点云进行配准,关键点检测模块被放置在密集膨胀图卷积模块后用于点云稀疏表示的获得,该模块通过观察特征的L2规范表明一个点是否重要。使用XP与YP表示源点云与目标点云通过关键点检测模块检测的P个关键点的集合,表示为:
其中,topP(·)表示选择给定输入的P个最大元素的索引,Gxzong与Gyzong表示源点云与目标点云经过密集膨胀图卷积模块的输出,‖·‖2表示L2规范。
1.4 离群点过滤模块
尽管关键点检测模块可以提取源点云X与目标点云Y中更利于匹配的关键点,但是在关键点集合XP与YP中仍然存在没有对应关系的点,这些点称为离群点。为了防止这些离群点对于配准的影响,本文使用了基于深度神经网络的离群点过滤模块,该模块是对于2D离群点过滤网络的扩展。模块的输入是假定的对应关系,该对应关系通过对关键点检测模块输出的三维特征进行级联操作得到,记为Z={zi∈ℝ6|i=1,2,…,P}。模块的输出为输入点对所对应的权值,记为w。为了增强配准模型的鲁棒性,将其加入式(1)中来获得封闭形式的解:
其中,wi的取值范围为0~1,当其值为0时,xi与ym(xi)为离群点,值越大点对匹配度越高。式(10)的求解过程将在奇异值分解模块中详细展开。文献[24]指出,利用适当的标准化可以有效地过滤掉离群点,因此对现存的标准化[24-25]进行了扩展,使其可以应用到处理点云配准任务当中。所提出的离群点过滤模块如图5所示,该模块由两个残差块1与一个残差块2构成。
模块将两个点上下文标准化模块(point context normalization,PCN)进行串联,并执行跳层连接融合底层特征来构成残差块1。其中所使用的单例标准化(instance normalization,Instance Norm)[26]被用来编码全局上下文信息,使用统计数据对每个点对进行处理,并嵌入全局信息,可以很大程度上提高性能。批标准化(batch normalization,Batch Norm)[27]被用来加快网络的收敛速度。其次,还使用1×1卷积将特征映射的分布标准化到所有的点对中。残差块1的输出zr1i可以表示为:
其中,PCN2(·)表示两层PCN。
与残差块1类似,残差块2由两个注意力上下文标准化(attentive context normalization,ACN)与一个跳层连接构成。对于残差块1的输出zr1i,分别利用局部与全局两种注意力机制获取clocali与cglobali:
可以观察到,式(12)中的局部注意力机制独立的作用于zr1i,而式(13)中的全局注意力机制将zr1i与其他点云对进行了集合。此外,为了同时考虑到多种注意力,将两种权重进行简单的结合得到点云对自身的自权重czongi:
对于所获得的czongi,使用μc(zr1i)和σc(zr1i)表示zr1i的加权平均值和标准差,注意力标准化(Attentive Norm)可用以下公式表示:
使用ACN2(·)表示两层ACN,则残差块2的输出zr2i可以表示为:
对于输入点云对,对应的权值w可以通过以下公式得到:
其中,tanh(·)表示双曲正切激活函数,ReLU(·)表示整流线性单元激活函数。
1.5 奇异值分解模块
为了获得最优的旋转参数与平移参数,本文选择使用奇异值分解模块。奇异值分解模块的输入为关键点检测模块的输出XP、YP与离群点过滤模块的输出w。首先,使用Gumbel-Softmax获得点云YP中xi的对应点ym(xi)。利用w,可以通过下列公式计算xi和ym(xi)的加权中心:
加权协方差矩阵S为:
其中,W=diag(w1,w2,…,wP)。在经过奇异值分解后:
可以得出转换参数R与t,表示为:
1.6 损失函数
本文的损失函数共包含两部分:周期一致性损失Lcn与全局特征对齐损失Lng。
使用Rnxy、txn y表示从点云X到点云Y的转换参数,Rnyx、tyn x表示从点云Y到点云X的转换参数,则Lnc表示为:
其中,Ψxn、Ψyn是对Gxzong与Gyzong进行平均池化得到。由此,最终的损失函数可以表示为:
在训练期间,将源点云与目标点云输入到所提出的配准网络n次,即进行n次迭代。
2 实验结果与分析
2.1 实验数据与设置
本文选用三个数据集评估本文所提出的DORNet(dilated graph convolution and outlier filtering for partial registration network)模型的性能,这三个数据集为ModelNet40[28]、ShapeNetCore[29]与Real Data[30]。首先,采样含有1 024个点的源点云X。之后,沿着每个轴,使源点云随机进行刚性变换生成目标点云Y,每个轴的旋转范围为[0,45],平移范围为[-0.5,0.5]。之后,通过在X与Y中随机选取一个点并获取其最近点的768个点来模拟残缺点云。
本文将DORNet与ICP、Go-ICP、FGR(fast global registration)、PointNetLK、DCP、PRNet、FMR、IDAM与LPD-Pose-Iter进行了比较。实验所使用的配置如表1所示。

表1 实验配置Table 1 Experimental configuration
对于ModelNet40数据集与ShapeNetCore数据集,本文设置初始学习率与epoch分别为0.001和100。在epoch分别为30、60、80时,学习率除以10。对于Real Data数据集,由于模型较少,将学习率与epoch分别设置为0.000 1和50,学习率在epoch为30时除以10。在训练过程中取迭代次数n为3,即X和Y都会迭代地通过DORNet传递3次(X的位姿会更新3次,更新所需要的转换参数见式(3))。
为了便于比较性能,本文计算了旋转参数R和平移参数t的真实值和估计值之间的均方误差(mean square error,MSE)、均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)和拟合系数(coefficient of determination,R2)。对于拟合系数来说,数值越接近于1,模型拟合度越好。除了拟合系数,其余指标数值越低,代表模型配准效果越好。
2.2 对比实验
2.2.1针对ModelNet40数据集的配准实验
ModelNet40数据集包含40个类别,共计12 311个计算机辅助设计(computer aided design,CAD)模型。为了验证DORNet的有效性、广泛性以及鲁棒性,在ModelNet40数据集上分别进行三种不同的实验:模型类别已知的配准实验、模型类别未知的配准实验和添加高斯噪声的配准实验。
2.2.1.1 模型类别已知的配准实验
模型类别已知是指训练使用的模型类别与测试使用的模型类别一致。在实验中,将ModelNet40数据集中9 843个模型用于训练,剩下的2 468个模型用作测试。实验结果如表2所示。指标后加R代表使用旋转参数的估计精度,指标后加t代表使用平移参数的估计精度。↓代表计算所得数值越低效果最佳,反之使用↑。为了便于观察模型的性能,将最佳结果使用加粗的形式来突出显示。可以看出,本文的网络无论是在旋转参数R还是平移参数t上的误差明显低于其他模型。图6显示了经过DORNet配准的残缺点云示例,红色点为源点云,蓝色点为目标点云。第一行与第二行分别为配准前与经过DORNet配准后的结果。可以清楚地看出,经过DORNet配准后的点云,多数点都可以正确匹配。
2.2.1.2 模型类别未知的配准实验
模型类别未知是指训练使用的模型类别与测试使用的模型类别不一致。本文将ModelNet40数据划分为两部分,取其中的20个类别作为训练,其余的20个类别作为测试。表3列出了DORNet与其他模型比较的结果。从表3中可以看出,由于训练使用的模型与测试使用的模型属于不同类别,与模型类型已知的结果相比,模型配准性能有所下降。但所提出的算法的精度仍为最优异的,这验证了所提出模型的泛化性。

表2类别已知的残缺点云配准实验结果Table 2 Experimental results of partial point cloud registration with known categories

表3类别未知的残缺点云配准实验结果Table 3 Experimental results of partial point cloud registration with unknown categories
2.2.1.3 添加高斯噪声的配准实验
在真实场景中,由于扫描设备的误差,对所获得模型有一定的影响。使用添加高斯噪声的实验来模拟这一情况,所添加的高斯噪声的均值为0,方差为0.01,缩放范围为[-0.05,0.05]。模型添加高斯噪声前后的对比如图7所示。左边为添加高斯噪声前的可视化结果,右边为添加高斯噪声后的可视化结果。实验结果如表4所示,可以明显地看出,各项性能指标相比表2,所有模型的性能相较于没有添加高斯噪声的实验性能有所下降,但是本文模型的实验误差仍然低于其他模型。这是由于所使用的离群点过滤模块给予不匹配的点对低权重,降低它们在配准过程中的重要性,这使得DORNet在面对添加高斯噪声的影响时更具有鲁棒性。
2.2.2 针对ShapeNetCore数据集的配准实验
为了进一步验证模型的配准能力,本文选择了数据量大于ModelNet40的数据集ShapeNetCore来进行实验。该数据集包含来自55个类别的51 127个预对齐模型。本文使用35 708个模型用于训练,15 419个模型用于测试,将DORNet与在ModelNet40数据集上相较于其他模型表现较好的PRNet、IDAM与LPD-Pose-Iter进行比对。表5显示了配准结果,可以明显地看到,DORNet在每个指标上的结果都优于其他三种算法。

表5 ShapeNetCore数据集的残缺点云配准结果Table 5 Experimental results of partial point cloud registration on ShapeNetCore dataset
2.2.3 针对Real Data数据集的配准实验
本文还利用Real Data数据集中的Stanford Bunny(斯坦福兔子)对模型进行了测试,该数据中仅包含由传感器扫描得到的10个真实点云数据。与ModelNet40数据集与ShapeNetCore数据集中的点云数据相比,该数据集中的点云分布并不均匀,因此在Stanford Bunny上的配准实验更具有挑战性。图8显示了配准结果。左边为配准前的点云,右边为配准后的点云。此外,值得一提的是,本文并未在Stanford Bunny上进行训练,而是使用在ModelNet40数据集模型类别已知配准实验中所获得的模型直接进行测试,这进一步说明了DORNet的泛化能力。
2.3 消融实验
为了验证模型每个模块的有效性,在ModelNet40模型类别未知的数据集上进行了有关残缺点云配准的消融实验。本文模型包含三个重要组成部分:膨胀图卷积块(DGCB)、密集连接(DN)与离群点过滤模块(OFM)。将消融实验分为以下几个部分:
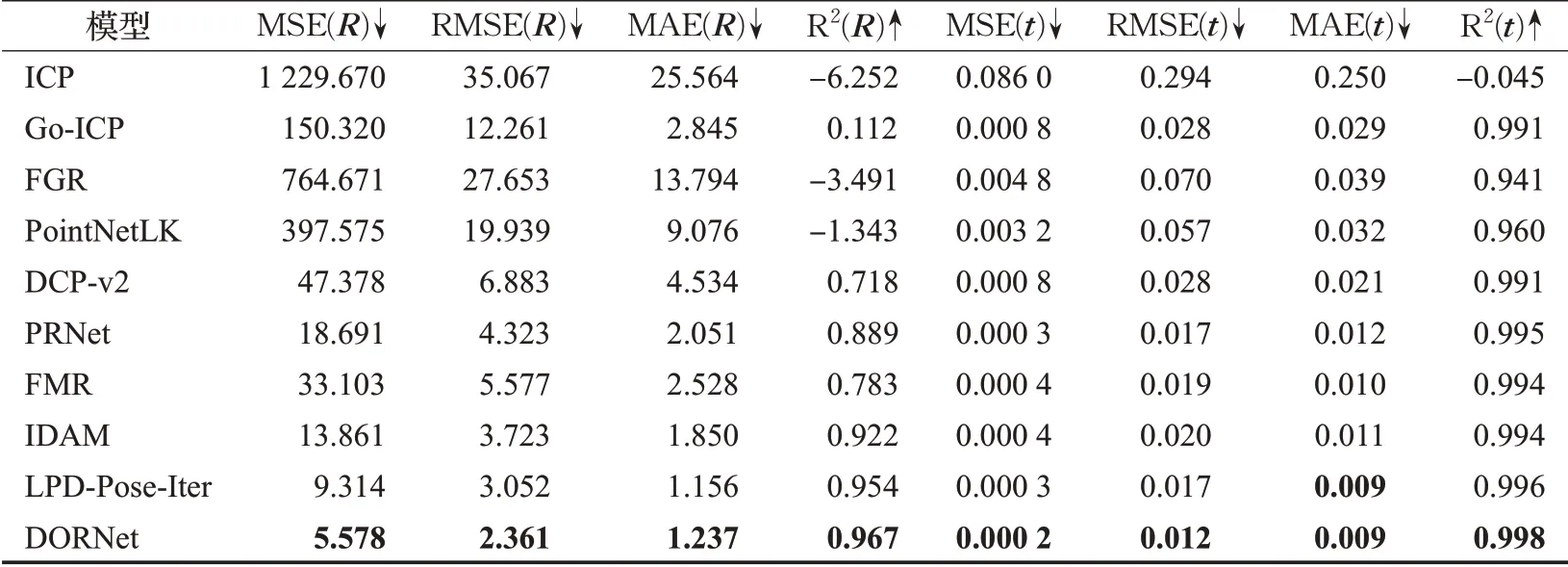
表4带有高斯噪声的残缺点云配准实验结果Table 4 Experimental results of partial point cloud registration with Gaussian noise
(1)DORNet:网络包含上述三个组成部分,即所提出的完整网络。
(2)DORNet w/o DN:在密集膨胀图卷积中,不使用密集连接网络来处理DGCB的输出。使用完整的离群点过滤模块过滤离群点。
(3)DORNet w/o DN&DGCB:在密集膨胀图卷积模块中,使用简单的KNN生成图特征,且不使用密集连接。使用完整的离群点过滤模块过滤离群点。
(4)DORNet w/o DN&DGCB&R1:在密集膨胀图卷积模块中,使用简单的KNN生成图特征,且不使用密集连接。在离群点过滤模块中,去除残差块1(R1),即仅使用残差块2(R2)过滤离群点。
(5)DORNet w/o DN&DGCB&R2:在密集膨胀图卷积模块中,使用简单的KNN生成图特征,且不使用密集连接。在离群点过滤模块中,去除残差块2(R2),即仅使用残差块1(R1)过滤离群点。
(6)DORNet w/o D&DGCB&OFM:在密集膨胀图卷积模块中,使用简单的KNN来生成图特征,且不使用密集连接。不使用离群点过滤模块过滤离群点。
表6显示了消融实验的结果。除了在对比实验中所用的4个指标,本文增加了一个衡量网络效率的指标Time。可以看出,随着模块的减少实验精度不断下降,说明每个模块都可以提高模型的配准性能。此外,在DORNet w/o DN&DGCB中,即不使用密集膨胀图卷积模块时,与完整的DORNet相比,网络的配准性能会大幅度下降。以旋转参数相关指标举例,DORNet与DORNet w/o DN&DGCB相比,MSE、RMSE与MAE的误差分别减小了230%、80%与90%,而速度仅下降了10%。这说明所使用的密集膨胀图卷积模块对于网络是具有正向意义的。此外,DORNet w/o DN的实验结果也表明对膨胀图卷积的输出进行密集连接,在一定程度上提高了网络配准残缺点云的精度。最后,为了验证离群点过滤模块的合理性与有效性,提供了DORNet w/o DN&DGCB&R1、DORNet w/o DN&DGCB&R2与DORNet w/o DN&DGCB&OFM的实验结果。可以看出,去掉残差块1或者残差块2的离群点模块,相比DORNet w/o DN&DGCB(使用完整的离群点过滤模块)配准误差均有所上升,且误差均低于DORNet w/o DN&DGCB&OFM(不使用离群点过滤模块),这验证了所提出离群点过滤模块的合理性。其次,也提供了离群点过滤模块过滤离群点的可视化结果,如图9所示,绿色线连接的点对为过滤的离群点。从图中可以看出,相比于去掉离群点过滤模块中的残差块1(DFM w/o R1)与去掉离群点过滤模块中的残差块2(OFM w/o R2),完整的离群点过滤模块可以过滤掉更多的离群点,这进一步说明了离群点过滤模块的有效性。

表6 类别未知的残缺点云配准消融实验结果Table 6 Ablation experimental results of partial point cloud registration with unknown categories
3 结束语
针对残缺点云配准,本文提出了DORNet网络。一方面,利用密集连接与膨胀图卷积块构成的密集膨胀图卷积模块有效地提取点云的细粒度特征。另一方面,利用基于深度网络与标准化相结合的离群点过滤模块,根据输出点对不同的对应权重过滤掉不匹配的点对。最后,将点对权重加入奇异值分解模块获得配准残缺点云所需要的转换参数。在ModelNet40、ShapeNetCore以及Real Data数据集上进行配准实验,结果表明了所提出的网络不仅具有良好的鲁棒性,也具有一定的泛化能力。
