基于PCA-ILARS-DNN案例推理模型的电站设备故障诊断方法
2022-11-19徐天宏陈荣泽司风琪
徐天宏,王 鹏,汪 勇,陈荣泽,司风琪
(1.东南大学 能源热转换及过程测控教育部重点实验室,南京 210096;2.上海发电设备成套设计研究院责任有限公司,上海 200240)
近年来,工业过程安全生产问题越来越受到关注,故障监测与诊断作为工业过程重要手段,在国内外众多学者的研究和探索中,已经取得了一定的进展。工业过程的状态监测及故障诊断总体可分为基于解析模型的方法和基于数据模型的方法[1]。基于解析模型的方法是通过对研究对象进行机理分析,建立数学模型,根据数据实际值与模型预测值的残差进行状态分析。该方法在简单的研究对象中可以取得不错的效果,但随着工业生产规模的不断扩大,设备运行特性越来越复杂,建立解析模型的难度也越来越大。因此,通过对历史运行数据进行分析,从而实现工业过程中状态监测及故障诊断的数据模型方法受到了关注[2]。常见的基于数据的故障诊断方法有多元统计方法、机器学习方法等[3]。多元统计方法一般通过概率模型来监测故障,对新类型故障的识别诊断率不高[4];机器学习方法需要高质量的数据样本来保证故障诊断模型的准确性[5],而复杂多样的电站设备数据并不能满足此要求。
基于案例推理的故障诊断方法,作为数据模型方法的一类,通过模拟人类的思考过程,提取现有关键信息按照推理逻辑,在故障诊断领域取得了一定的成果[6]。通过案例表示可提取故障信息构建案例库,并基于案例库检索相似案例从而达到高效诊断的目的,以及通过案例更新实现自动更新模型[7]。近年来,基于案例推理的故障诊断方法被广泛用在农业信息决策、车辆交通规划及紧急事件处理上[8-10]。
在基于案例推理的故障诊断流程中,案例表示是构建故障案例库的基础。栗宇[11]使用本体理论对汽轮发电机组的故障关系进行表示,通过系统定义整个汽轮发电机组之间的知识关系,构建汽轮发电机组典型故障案例库。但对于电站设备故障诊断来说,故障信息由故障的相关参数的历史数据构成,不需要使用本体理论表示其中的知识关系,因此应选取故障案例的数据表示方法。传统的故障诊断过程大致可以分为故障监测、故障隔离和故障识别三个阶段。ALCALA C F等[12]从故障隔离的角度出发提出使用相关变量组合作为故障表示方法,并通过匹配变量组合来实现故障识别。但该方法需要人工设置阈值,并且无法将故障量化,导致诊断率偏低。
案例检索是案例推理流程中用于诊断案例状态类属问题的方法。它通过计算案例之间的相似度,寻找最相似案例进行匹配。近年来,神经网络因其强大的特征提取和拟合能力在监督学习领域取得了显著的成果。因此,相比于其他算法,在案例检索过程中使用神经网络算法可以取得较高的诊断识别率[13]。
鉴于上述方法的优缺点,笔者提出了基于主成分分析(PCA)-改进最小角回归(ILARS)-深度神经网络(DNN)案例推理模型的电站设备故障诊断方法。基于PCA-ILARS算法进行案例表示来提取故障信息,构建具有统一特征状态的案例库,然后采用基于DNN的案例检索算法实现故障诊断,并通过电站磨煤机的真实故障案例进行验证与分析。
1 相关算法
1.1 PCA算法
PCA算法是一种经典的故障监测方法。设观测的历史数据用X∈Rm×n表示,X为由实数组成的向量,X=[x1,x2,x3,…,xm]T。根据X的平均数和方差对数据进行归一化,其协方差矩阵S可表示为:
(1)
对S进行特征值分解得到:
(2)
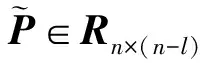
PCA模型主要采用统计量SPE(Square Projection Error)指标(用SPE表示)和T2(Hotelling)指标来进行故障监测。
SPE用来的监测变量X在残差空间的映射,即
(3)
(4)
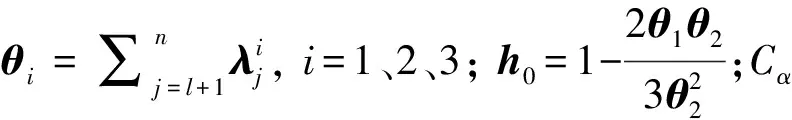

T2用来的监测X在主成分空间的映射,即
T2=XTPΛ-1PTX=XTDX
(5)
(6)
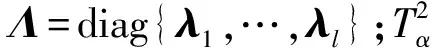
1.2 PCA-ILARS案例表示方法
基于PCA模型,将故障案例通过ILARS案例表示方法提取案例数据。
最小角回归(LARS)算法是一种经典的故障隔离算法,是通过逐步逼近目标来解决稀疏回归的问题[14]。
(7)
采样时间间隔为15 s,通过ILARS算法,将观测量(见图1)X∈R1×n提取生成数据样本D∈R1×n,n为参数数量。
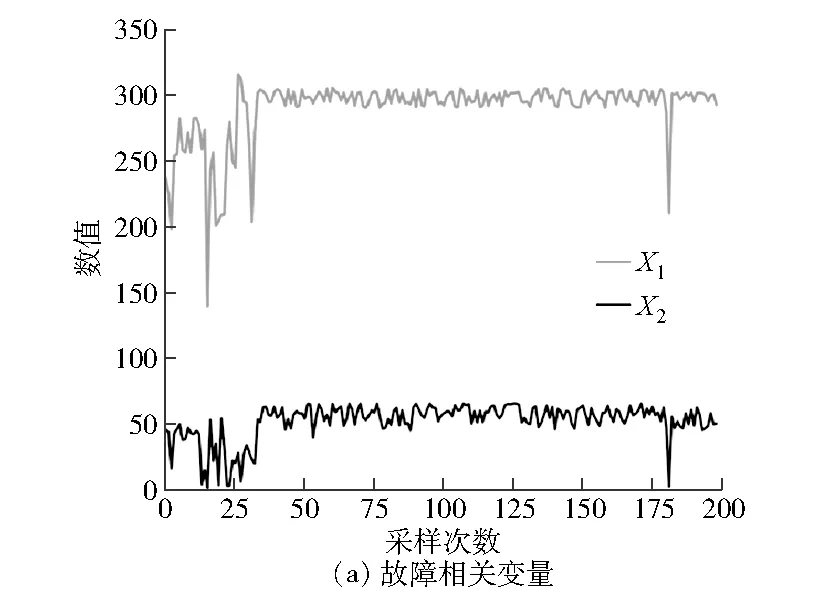
图1 原始数据时序图
所研究的稀疏回归问题如式(8)所示。
(8)
算法首先设置变量活动集A,并通过对变量与当前残差的相关度来选择最大相关度变量加入,其与前向选择方法类似,都是逐步地进行,每步增加一个变量到活动集中,但不同点是最小角度是当目前变量和下一个变量与当前残差具有相同的相关度时,加入另一个变量到活动集,达到回归预测的精度时停止计算,并记录每次残差的变化值MSE和变量变化的步长β。
由于M是对称正定矩阵,根据Cholesky分解,存在V使得M=VVT,则式(8)可转化为:
s.t.{β|∀β,MSE≤ξ}∩‖β‖0=t
(9)
式中:ξ为限值;t为迭代次数。
通过ILARS算法逐渐逼近故障方向,当监测指标小于限值时停止,可实现对观测值x的故障分离。
故障案例D可表示为:
(10)
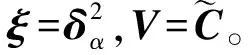
(1)初始定义β为零矩阵,X为任意时刻被检测为故障的观测值向量;活动集A为空集。
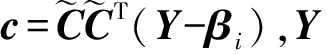
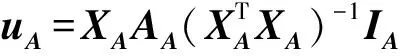
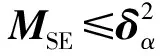
(5)根据βi平均分配每次迭代的MSE,将分配的MSE作为案例样本D提取出来。
以图1为基准的PCA-ILARS案例表示时序图见图2。

图2 PCA-ILARS案例表示时序图
1.3 DNN
DNN也称多层感知机(MLP),是具有多个隐藏层的神经网络。按不同层的位置划分,DNN内部的神经网络层由第一层的输入层、中间层的隐含层和最后一层的输出层组成(见图3)。层与层之间是全连接的,第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。每个神经元在激活函数σ(z)处满足z=∑Wixi,其中:Wi是第i层神经元的权值,xi是第i层的输入值。
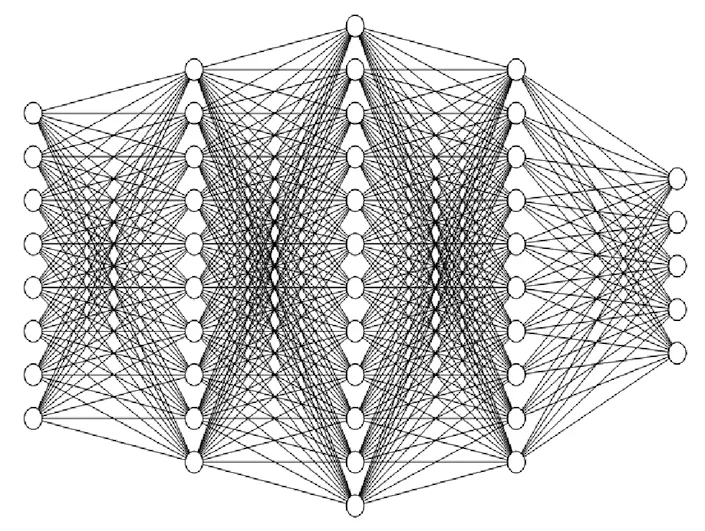
图3 DNN结构图
DNN可使用梯度下降法进行训练,即
(11)
式中:η为学习率;C为损失函数;wij(t)表示第t次训练时第i层的第j个节点的权值。
2 基于PCA-ILARS-DNN案例推理模型的故障诊断方法
案例推理理论属于人工智能领域的算法。特定领域的知识可通过案例表示储存在案例库中,然后利用案例检索算法比较新案例和旧案例的相似度,从而得到正确的解决方法。案例推理通常由案例表示、案例检索、案例应用、案例修正、案例保存等构成。
基于案例推理的故障诊断具体流程见图4。利用故障监测模型获取故障状态的常规信息,通过PCA-ILARS案例表示方法将常规信息转变为统一形式的故障案例,并利用案例检索找到相似案例进行匹配。如果案例相似度大于匹配阈值,则进行案例应用与修正,并将成功应用的案例进行保存与更新学习。否则,则需要利用外部专家知识对案例进行人工标注,案例经修正后应用于现场,并将成功应用的案例进行保存与更新学习。
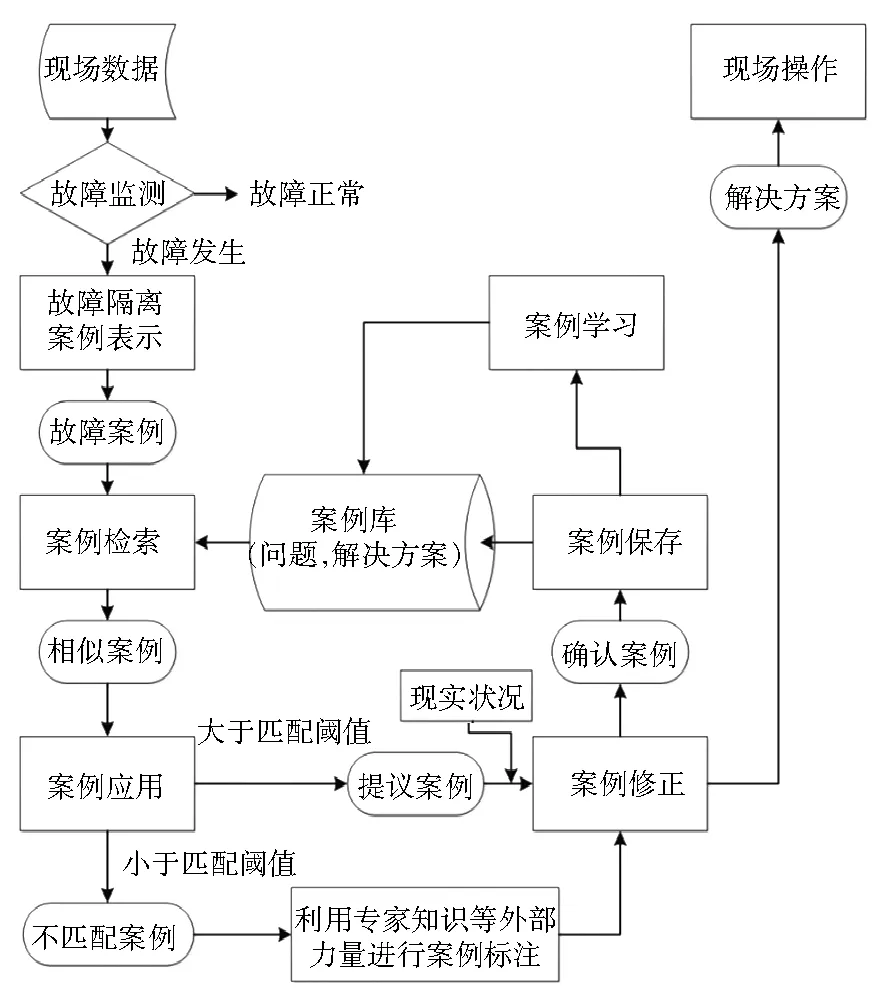
图4 案例推理故障诊断流程图
具体的案例检索过程见图5。
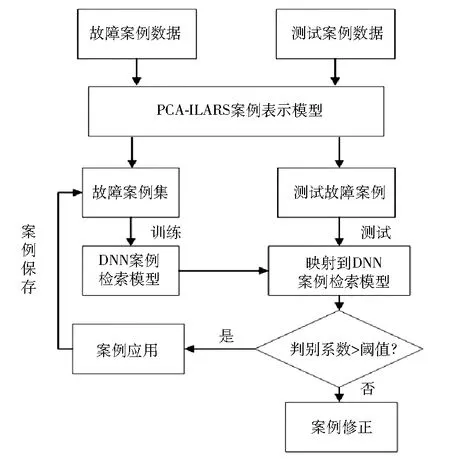
图5 基于PCA-ILARS-DNN案例检索流程图
首先,运用PCA-ILARS算法将故障数据提取成故障案例,构成故障案例库。其次,将案例库中的案例数据预处理之后,利用故障案例库中的带有标签的案例训练DNN,生成DNN判别模型。当需要诊断的案例数据首先经由PCA-ILARS算法提取为诊断案例,数据预处理之后,通过DNN判别模型进行训练,DNN判别模型最后一层的激活函数采用softmax函数表示为:
(12)
式中:zi表示最后一个隐含层的节点输出;k为输入节点个数;yi为输出值。
若输出层节点最大值大于阈值,则认为该节点表示的类型为故障类型,输出结果,进行案例应用,并将判别类型放入故障案例集中保存。输出层中若没有节点数值大于阈值,则为匹配失败,为待审核故障案例,需要通过专家人工修正,判断是否采用新故障案例进行处理。阈值θ为经验系数,一般选取所有训练集softmax输出层节点最大值组成集合中的最小值。
(13)
式中:yi为softmax节点输出值;k为输出层节点个数;m为训练样本数。
3 电站磨煤机故障算例
以某电站磨煤机为对象,验证所提方法的故障诊断效果。首先,根据磨煤机的运行特性,选择与磨煤机相关的27个变量参数建立故障诊断模型,并选择40个真实故障案例的13 220个数据点作为样本数据。其中,故障包括磨煤机棚煤、液压跳闸、拉杆断裂、拉杆脱落和清扫链跳闸。磨煤机相关参数见表1。

表1 磨煤机相关参数
为验证PCA-ILARS案例表示算法的优势,与原始的案例表示方法和经典的故障隔离算法进行对比,并通过DNN检索模型验证结果准确率。DNN模型的训练集分别由案例总数的5%、10%、20%、30%、50%的比例按照时序等间隔选择样本组成,测试集为全部样本。将所有案例作为测试集进行测试。算例中DNN模型设置为5层,每层的节点数分别为27、32、64、32和5。层与层直接选择全连接方式,节点的激活函数除最后一层输出层使用softmax激活函数外,其余层均使用tanh激活函数,学习率设置为0.001,寻优方法为RMSprop,损失函数为交叉熵,评价指标为准确率。使用Python平台的库设置相关参数来搭建DNN模型。准确率为正确分类样本数与总样本数的比值。
将案例相关的27个参数的历史数据作为原始数据,分别通过数据表示、故障隔离表示和PCA-ILARS算法表示。图6~图8是磨煤机棚煤案例的故障相关参数和无关参数用数据表示、故障隔离表示和PCA-ILARS算法表示的时序图。由图6~图8可以发现:磨煤机棚煤时,数据表示方法无法直观观察故障变化;故障隔离方法可以诊断出故障发生,但是无法量化故障发生的程度;PCA-ILARS算法表示显现出给煤机瞬时质量流量和出口一次风温随着时间的变化逐渐变大,这与实际情形下的故障特征一致,说明此方法有一定的物理意义。
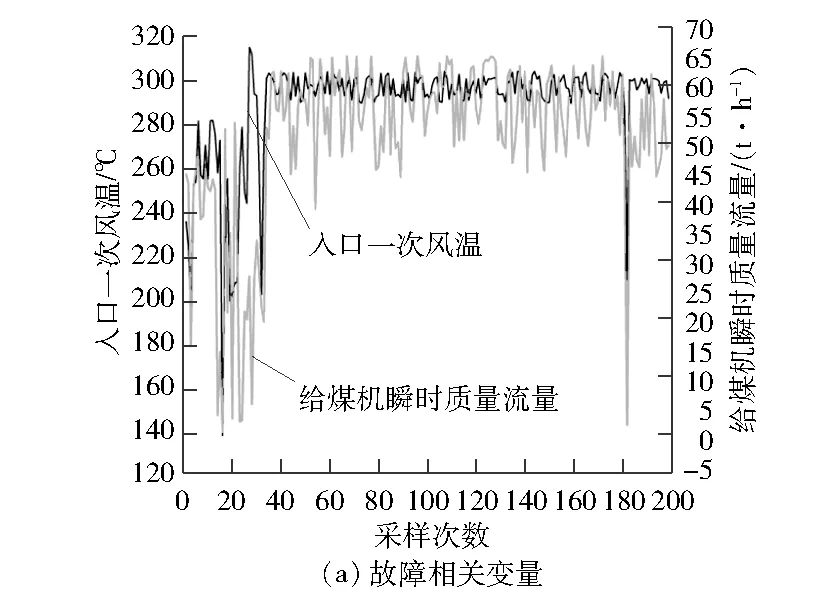
图6 磨煤机数据表示时序图

图7 磨煤机参数故障隔离表示时序图
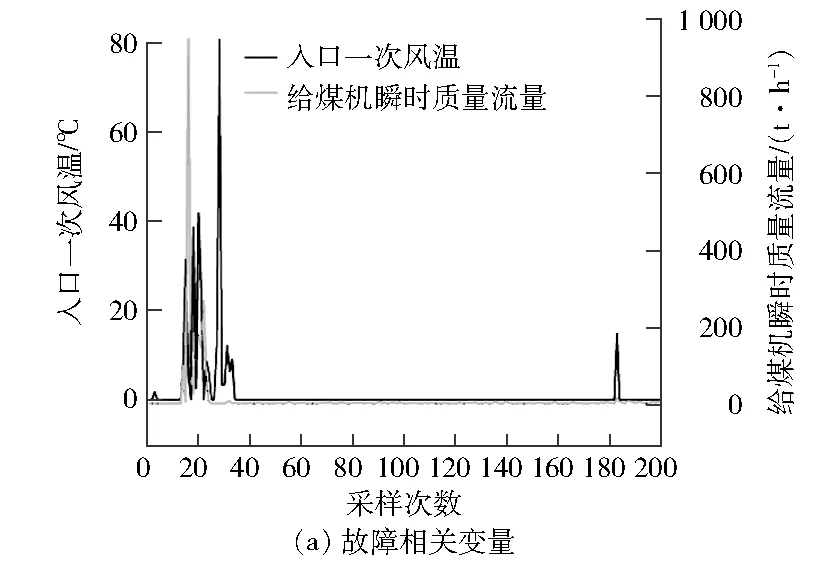
图8 磨煤机参数PCA-ILARS算法表示时序图
为进一步对比PCA-ILARS算法提取特征的优势,将参数通过数据表示、故障隔离表示和PCA-ILARS算法表示后通过降维算法投影到二维空间(见图9)。可以发现,数据表示方法无法区分故障,而故障隔离方法和PCA-ILARS算法能够将故障大致分离,并且PCA-ILARS算法的分离效果更好。
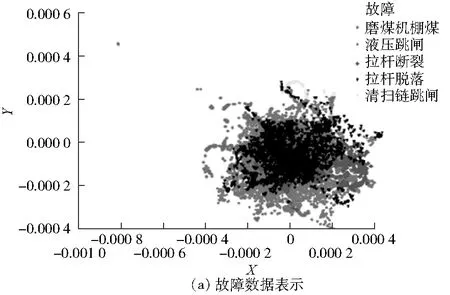
图9 二维空间散点图
为验证PCA-ILARS算法对于故障检索的影响,将案例表示后经基于DNN的案例检索模型进行诊断。不同训练样本比例的诊断结果见表2。PCA-ILARS算法表示的样本经DNN案例检索模型后的诊断率可以达到96.2%以上,大于数据表示和故障隔离表示的诊断率,达到工业过程故障诊断的要求。

表2 基于DNN的案例检索方法与其他方法处于不同训练样本比例下的准确率
4 结语
针对故障诊断率不高的问题提出了一种基于PCA-ILARS-DNN案例推理模型的故障诊断方法。先通过PCA-ILARS算法对故障原始案例进行表示,接着使用DNN案例检索模型进行故障诊断,并使用磨煤机真实故障案例进行验证。主要结论如下:
(1)为更好地提取故障信息和特征,提出了PCA-ILARS算法,并与数据表示和经典故障隔离表示进行对比,结果证明PCA-ILARS算法具有更有效地提取有关参数与无关参数的特征。
(2)针对故障诊断过程准确率低的问题,提出了PCA-ILARS-DNN的案例推理方法,结果表明此方法优于传统的故障诊断方法,可以达到故障诊断要求,提高电站设备运行的安全性。
(3)构建了基于案例推理的故障诊断模型,案例的保存保留了案例信息的时序特性,为后续提取动态特征等提供了基础模型。
