基于神经网络的高并行大规模MIMO信号检测算法

许耀华, 朱成龙, 王 翊, 蒋 芳, 丁梦琴, 王慧平

(安徽大学计算智能与信号处理教育部重点实验室, 安徽 合肥 230601)

0 引 言

大规模多输入多输出(multiple input multiple output, MIMO)系统是5G的关键技术之一,高频谱效率和足够的空间自由度使得其成为学术界研究热点。大规模MIMO也面临许多挑战,如信号接收检测[1]。由于检测问题是非确定性多项式(non-deterministic polynomial, NP)完备问题,计算复杂,已有多项式复杂度的次最优解决方案。机器学习领域的深度神经网络在解决很多工程领域问题上的成功,表明基于机器学习数据驱动的检测方法具备计算效率高、接近最佳的检测性能的特点[2]。

在大规模MIMO检测算法中,最大似然估计(maximum likelihood, ML)算法穷尽搜索方式找到最优解,但却有着指数级的复杂度,随着天线数量的增多,在实际系统中难以实现[3]。为了降低ML算法的计算成本,人们开始寻求近优的检测算法。长期演进(long term evolution, LTE)系统小规模MIMO检测通常使用线性检测算法,如迫零(zero forcing, ZF)算法和最小均方误差(minimum mean square error, MMSE)算法[4-5],基于矩阵求逆,诺依曼级数近似(Neumann series approximation, NSA)算法将其转换为一系列矩阵矢量乘法[6]。随着5G大规模MIMO用户数的增加,其计算复杂度也变得相当大,这些算法在实际系统中难以实现。为了进一步降低矩阵求逆带来的计算复杂度,Li等[7-8]提出了一种高并行(high-parallelism, HP)检测算法,通过构建迭代矩阵将复杂的原矩阵反转为线性方程组进行求解,并详细证明了其收敛性,算法并行实现方法和复杂度分析表明,并行度可以与矩阵维数相同,与传统的MMSE算法相比,复杂度可以降低一个数量级。

近年来,在计算机视觉与自然语言处理等领域,深度学习得到了广泛的应用。同样,有部分学者开始将深度学习方法应用到通信领域[9-11],通过许多的非线性单元和神经网络的结构,从而设计出适用于信号检测方面的神经网络,例如Samuel等[12-13]基于投影梯度下降法提出了基于模型驱动的信号检测网络(detection network, DET-Net),将ML与梯度下降算法相结合,生成一个神经网络架构;张晓羽等[14]提出了一种去噪稀疏的连接检测网络(denoising sparsely connected detection network, DS-Net), 通过将全连接网络修改为稀疏连接的简化网络,从而在一定程度上减少了训练参数;胡钟秀等[15]通过在原有的简化近似消息传递(simplified approximate message passing,SAMP)迭代检测器中增加一些可训练参数,利用深度学习的方法获得最优参数提出简化近似消息传递网络(simplified approximate message passing network, SAMP-Net),提高了原迭代检测器的性能等。对于设计深层网络架构的比较有前景的方式将是对现有迭代算法的展开,将迭代算法的每一次迭代过程视为神经网络中的一个层级,从而将迭代算法变成深层网络结构。

本文将深度学习与一种HP检测算法相结合,提出一种新的HP网络(HP network, HP-Net),用于MIMO检测。在不同的信道和不同信噪比(signal to noise ratio, SNR)的情况下,HP算法迭代收敛的速度并不相同,本文提出的方案中,将HP算法与深度学习结合,HP算法的每一次迭代作为一个单层网络,通过非线性神经元和相关权重偏置的训练,从而实现较低的误码率。

本文主要的研究工作如下:首先介绍MIMO系统模型和MIMO检测算法;然后描述了基于HP检测算法和深度学习提出的HP-Net神经网络结构;之后对传统的MMSE算法和HP检测算法以及HP-Net网络结构的检测性能进行了仿真对比分析;最后对全文进行相关总结。

1 系统模型和MIMO检测算法

1.1 系统模型

本文考虑大规模MIMO上行链路系统,如图1所示。用户数为K,基站端的接收天线数为N,并且K≪N。

图1 大规模MIMO上行链路系统

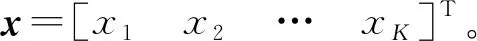
y=Hx+n

(1)

式中：H∈CN×K为复数信道矩阵;x∈CK×1为发送信号;y∈CN×1为接收信号;n∈CN×1为复加性高斯白噪声,且服从CN(0,δ2)分布(δ2表示方差)。

1.2 传统检测算法

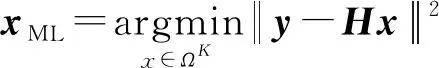
(2)

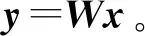
由式(2)可知:

W=HHH+δ2I

(3)

(4)

虽然MMSE属于近优算法,但由文献[16]可以得到,直接计算W-1的复杂度高达O(K3)。

2 HP-Net检测算法

2.1 HP信号检测算法

HP信号检测算法[7-8]是由Li等提出的一种低复杂度线性迭代算法,算法通过求解线性方程组的方式逼近计算出发送信号,进而通过判决恢复出原始信号。不同于传统的矩阵求逆,该算法通过构建迭代矩阵将复杂的原矩阵转换为对应线性方程组求解,从而避免对矩阵求逆的复杂求解。

将式(2)转化为式(5)的形式,通过对原矩阵W进行矩阵分解,将W等价为两个矩阵P和Q之和,其中P是一个非奇异矩阵,避免了对W-1的复杂求解。

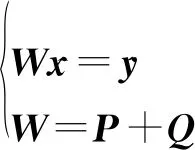
(5)

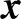
(6)

将式(6)进行线性迭代展开:

(7)

算法的迭代收敛条件为

(8)

在文献[7-8]中证明了在大规模MIMO系统中,式(8)是可以得到满足的。而对非奇异矩阵P可按以下步骤进行构建。将W分成若干个2×2子矩阵,分割后每行的子矩阵数量为M=K/2。因此,原矩阵W被分割为M×M的子矩阵,矩阵P是所有M个对角线子矩阵的组合结果,即矩阵P的方程为

(9)

式中:Pi, j和ωi, j分别表示P和W的第i行和第j列元素的值。

因此对P的求逆可以简单得到。通过式(9)可得矩阵P,对其求逆可通过对2×2子矩阵的求逆并行实现,2×2子矩阵求逆如下所示:

(10)

HP检测算法仅需一定的迭代次数,即可对复杂的矩阵求逆进行有效的避免,从而一定程度上降低复杂度,然而算法对于迭代次数并没有进行限制,并且并未明确算法的循环截止条件,流程如算法1所示。

算法 1 高并行信号检测算法输入 H,y,K,Titer,δ2初始化 W=HHH+δ2IPi,j=ωi,j, j-1≤i≤j, i mod 2=1ωi,j, j≤i≤j+1,i mod 2=00, 其他步骤 1 P-1=inv(P)Q=W-Py^=HHyx0=0步骤 2 for k=1:Titerxk+1=-P-1Qxk+P-1y^endfor输出 xTiter

2.2 HP-Net深度学习架构

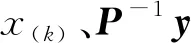
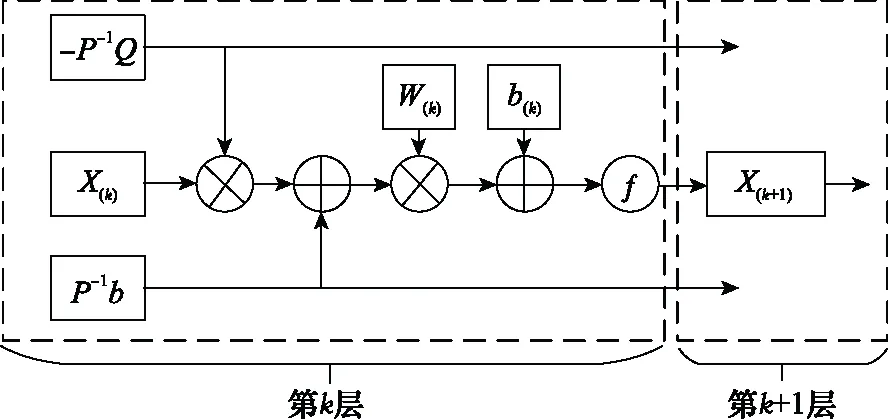
图2 一个HP-Net层的流程图

(11)

式中：f(·)由Relu函数表示。非线性阈值函数的选取有很多种[8],通过文献[14,16]可将阈值函数设置为

(12)

其中，t一般取0.000 1。

为了对神经网络更好的训练,从而得到最优的权重和偏置,对神经网络给出了对应的损失函数:

(13)

另外,利用了残差网络的思想,将每一层网络的输出于前一层网络的输出进行了残差运算。具体流程如算法2所示。

算法 2 HP-Net信号检测算法输入 H,y,δ2输出 x^初始化 W=HHH+δ2Iy^=HHyPi,j=ωi,j, j-1≤i≤j,i mod 2=1ωi,j, j≤i≤j+1,i mod 2=00, 其他步骤 1 P-1=inv(P)Q=W-Px(0)=0训练模型步骤 2 for k=1:LM(k)=-P-1Qx(k)+P-1y^R(k)=W(k)·M(k)+B(k)x(k+1)=f(R(k))endfor训练参数 Θ(k)={W(k),B(k)}s.t minimize loss(x;x^k)

将输入数据经过输入层输入到隐藏层,再将隐藏层得到的数据作为下一层的输入,每一层的输出将是下一层的输入,最后一层得到的输出再经过对应的非线性变换得到最后的结果。HP-Net将HP检测算法中的每一次迭代作为神经网络中的每一层,即神经网络的层数L与HP检测算法的迭代次数L相同,每一层的结果作为下一层的输出,并通过一个非线性阈值函数得到最终输出,如图3所示。

图3 HP-Net深层学习架构

2.3 复杂度分析

HP迭代算法矩阵求逆运算中,将原矩阵分解为若干个2×2的子矩阵。根据算法流程可知,计算复杂度主要集中在矩阵矢量乘法运算中,在k次迭代,K×K的矩阵Q和K×1的向量Xk进行乘法运算,其复杂度为(K-2)×K,其他运算的复杂度可忽略不计,在一次迭代中实现的并行性是K,所需的乘法是K2,从而整体上的算法复杂度为O(K2)[7-8]。

表1对比了HP算法、HP-Net与NSA[6]算法复杂度随迭代次数变化关系。与HP算法的表达式相比,HP-Net也没有复杂的矩阵求逆运算,其是基于HP算法与神经网络的结合,仅在训练中添加了部分可训练的参数Θ(k),从而增加了神经元节点间的乘法运算,因此复杂度是在HP复杂度的基础上加上神经网络参数训练的额外计算量O(K2)+O(K),但HP-Net整体复杂度数量级依旧没有发生改变,为O(K2)。另外,由于HP-Net在建立模型时为离线训练数据,模型训练参数可以被存储,因此检测过程中不需要重复训练网络,且经训练后的模型网络层数远低于HP算法的迭代次数,线上检测时模型仅需要计算有限次的矩阵乘法与加法,相较于经典检测算法的高复杂度,其整体检测复杂度更低。

表1 并行性与复杂度对比

表2对比了HP算法、HP-Net、MMSE算法与NSA算法整体复杂度的数量级,注意到MMSE算法与NSA算法的复杂度均为O(K3),因此HP-Net相对于MMSE与NSA算法的复杂度均降低了一个数量级。

表2 各检测算法复杂度

表3对比了HP-Net与经典DET-Net[12-13]算法的参数个数。由图2可知,单层HP-Net网络只有两个可学习参数,因此在总共L层的HP-Net架构中,可训练参数总数为2L。并且对于HP-Net网络架构,可训练参数数量仅与网络层数有关,不受用户数和接收天线数的影响,因此在训练过程中可以有效提高网络的收敛速度。此外,相对于DET-Net架构,HP-Net大大降低了训练次数以及训练参数,并能够实现相同甚至更好的误(bit error rate, BER)码率性能。因此,HP-Net能够成为实现大规模MIMO系统中快速信号检测的一个较好的实现方法。

表3 HP-Net与DET-Net架构对比

3 仿真分析

3.1 仿真背景

本文中使用Python3.6,在TensorFlow框架下构建神经网络,采用Adam Optimizer优化器进行训练参数优化[17]。初始值设置为0,初始学习率设置为0.000 1,并且学习率随着神经网络的层次的叠加发生对应的变化。在神经网络中,选取批量大小为3K(K代表1 000)个,迭代大小为10K个,用户端设置为16个单天线用户,基站端的天线数量设置为128个,调制方式为二进制相移键控(binary phase shift keying, BPSK),传输信道为瑞利衰落信道。以近优的MMSE算法作为参考,比较HP传统算法和基于深度学习的HP算法的性能。

3.2 结果分析

图4对HP检测算法与HP-Net架构在不同SNR的情况下BER性能进行了对比。从图4中可以看出,HP-Net算法相比于HP检测算法而言有着明显的优势,如在3层HP-Net算法比3次迭代的HP检测算法相比,BER为10-3时SNR提高了1.5 dB。并且,HP-Net算法在层数为3时BER性能已经超过了HP检测算法迭代11次的BER性能。

图4 HP-Net架构的BER性能对比

图5给出了MMSE算法、HP检测算法以及HP-Net架构在不同SNR情况下BER性能。仿真以MMSE作为参考对比,从图5中可以看出,HP-Net算法在层数为3时就十分接近于MMSE算法的性能,当层数为4时,BER性能已经超过了MMSE算法,这也是传统线性检测算法几乎无法达到的性能。

图5 各检测算法的BER性能对比

图6是信道SNR为10 dB,接收端天线数为128,网络层数设置为3 层时,对比HP-Net、HP算法与MMSE算法在不同用户数情况下的BER性能。以MMSE作为参考对比,由图6可知,在相同的仿真条件下,系统整体误码性能随着用户端用户数目的增加逐渐变差,其中可以发现HP算法变化最为明显。随着用户数增加,MMSE算法与HP-Net误码变化基本吻合,性能接近,因此在不同的用户数条件下,HP-Net算法能够在一定程度上逼近MMSE算法性能。

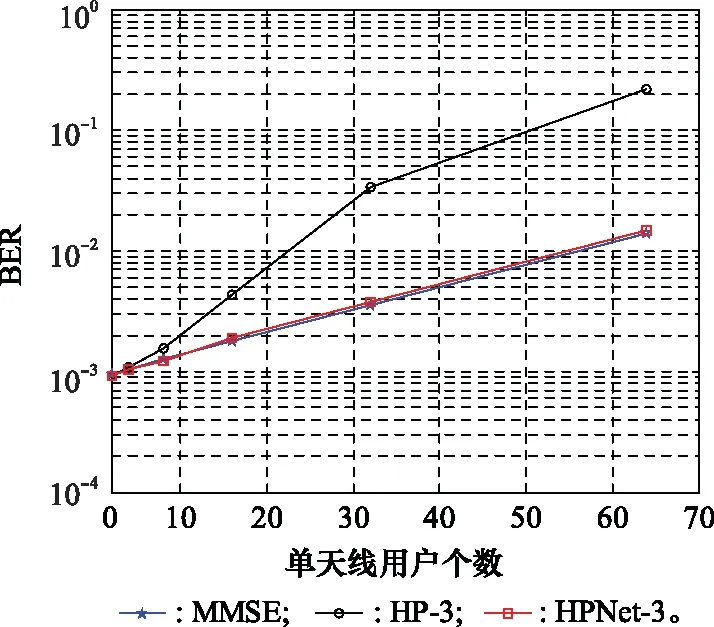
图6 HP-Net和MMSE算法与用户数的关系

图7给出了MMSE算法、DET-Net架构以及HP-Net架构在不同SNR情况下的BER性能。以MMSE作为参考对比,从图7中可以看出,在相同的仿真条件下,HP-Net算法在层数为3时即可达到DET-Net网络层数为14时的性能,在相同的网络层数时其性能远远优于DET-Net架构,且达到MMSE算法的性能时网络层数更少,性能更优。

图7 HP-Net与DET-Net架构的BER性能对比

图8是当SNR条件为10 dB时,HP-Net、MMSE、DET-Net以及HP检测算法的收敛情况对比。从图8中可知,随着层数(迭代次数)的不断增加,4种算法表现出明显不同的收敛情况。可以看出,当层数为3时HP-Net算法性能与MMSE算法接近,4层之后性能明显超出,而相较于传统的HP检测算法,HP-Net的性能优势更为明显,并且与DET-Net算法相比,在相同条件下收敛速度更快,BER更低。

图8 BER性能与迭代次数的关系

图9是当网络层数为3层,接收端天线数为128,SNR条件为10 dB时HP-Net与MMSE算法相对运行时间的对比,进而比较两种检测算法的计算复杂度。从图9中可以看出,随着用户端用户数目的增加,MMSE算法耗时上升趋势快速,而HP-Net耗时上升趋势相对平稳。因此,相较于MMSE算法,HP-Net在大规模MIMO信号检测中达到类似性能的计算复杂度较低。

图9 HP-Net算法和MMSE算法运行时间比较

4 结 论

本文对大规模MIMO上行链路系统的信号检测问题进行了研究,基于神经网络和一种HP检测算法提出了HP-Net网络架构,与在相同迭代次数下的HP检测算法进行对比,检测效果有了一定的提高,并且相比于MMSE算法,不仅复杂度有了明显的降低,而且还实现了更快的收敛速度和更优的BER性能。将传统的迭代算法与神经网络相结合,从而形成一定的深度学习网络架构,为信号检测算法与深度学习网络架构研究提供了一条途径。