数制转换改进方法

周全兴，李秋贤，吴冬妮

（凯里学院，贵州 凯里 556011）

0 引 言

数制[1]即进位计数制，是基于统一规则用一组固定的数字符号表示数值的方法[2]，数制包括两个重要概念——基数和位权。在计算机科学中，常见的数制有二进制（Binary）、八进制（Octal）、十进制（Decimal）和十六进制（Hexadecimal）。如表1 所示，二进制有2 个数字符号（0、1），其基数为2；十六进制有16个数字符号（0、1、2、3、4、5、6、7、8、9、A、B、C、D、E 和F），A 表示十进制数10，B 表示十进制数11，以此类推，其基数为16。位权，表示数码在不同位置上的权值[3]，即数制中某一位上的“1”所表示数值的大小，如十进制中第2 位位权为10、第3 位位权为100，二进制中第2 位位权为2、第3 位位权为4。

表1 常见数制的基数与位权

数值在计算机中是用二进制数表示的，为便于书写、表示和学习，引入了八进制、十进制和十六进制，如在《汇编语言》中，计算机指令代码即是用十六进制数表示的。各进制数之间的转换是所有计算机类相关课程中需要掌握的知识，由于内容复杂、课时较少，学生掌握起来有一定困难。笔者通过教学研究，总结出各进制数之间转换的高效方法，与传统方法相比，本文方法对提高教学质量和教学效果有很大的帮助。参考全国计算机等级考试，本文重点探讨数制转换中的整数部分。

1 各进制之间的转换方法

教科书中，从数制转换的基本原理出发进行梳理和讲解。为便于比较研究，对教科书中数制转换的方法进行介绍。

1.1 非十进制数转换为十进制数

对于N进制数，每个位置上数据所代表的大小等于数据本身乘以位权[4]，二进制数转换为十进制数即按照位权展开多项式求和的方法。

如：将二进制数1010 转换为十进制数，（1010）B=（ ）D。

同理可以实现八进制数、十六进制数转换为十进制数。

1.2 十进制数转换为非十进制数

对于十进制数转换为非十进制数，采用“除基取余法[5]”，即十进制数不断除以基数，取每一次余数，直至商为0，然后将余数“自下而上”排列即可[6]。

如：（25）D=（ ）B。

（25）D=（11001）B。

如：（125）D=（ ）O。

（125）D=（175）O。

如：（125）D=（ ）H。

（125）D=（7D）H。

1.3 二进制数与八进制数或十六进制数之间的转换

23等于8，24等于16，二进制数与八进制数、十六进制数有倍数关系[7]，在将二进制数转换为八进制数、十六进制数时，采用3 位二进制数换1 位八进制数（简称：3 位换1 位）、4 位二进制数换1 位十六进制数（简称：4 位换1 位）的方法。反之即采用1 位换3 位或1 位换4 位的方法。

如：（1101011）B=（ ）O=（ ）H。

（1101011）B=（ 153 ）O=（ 6B ）H。

如：（E06D）H=（ ）B=（ ）O。

（E06D）H=（1110000001101101）B=（160155）O。

采用此方法进行转换的过程中，位数不够的，在对应数前面加“0”，要注意例4 中加“0”可以省略（因为没有意义），但例5 中加“0”是不可以省略的，要注意二者之间的区别。

2 存在的问题

通过第1 节中对数制转换方法的梳理发现，二进制数转八进制数、二进制数转十六进制数是比较容易的，学生只需掌握相应数制的基数对应转换关系（或掌握一些特定数的对应关系），即可轻松掌握这部分知识。对于十进制与各进制的转换，虽然方法较为简单，但是由于计算比较复杂，计算的步骤也比较多，很容易混淆。例如在进行除基取余时，是自下而上还是自上而下？十进制与各进制的转换中，转换的数值较小，当数值较大时，采用除基取余计算，计算的复杂度与所花费的时间都会大大增加，如将十进制数2 049 转换为二进制数，甚至是32 769 呢，将要短除多次，同时在短除过程中也难免会出现错误。教学研究发现，通过一定的技巧和方法改进，可以解决以上难题，帮助学生在考试计算过程中节省宝贵时间。

3 改进方法

基于1.3 节知识，二进制数与八进制数或十六进制数之间的转换，目前通过3 位换1 位与4 位换1 位（或1 位拆3位与1 位拆4 位）的方法，比较快速直接，暂无改进方法。本文主要研究二进制与十进制相互转换，八进制、十进制与十六进制相互转换的改进方法。研究总结的改进方法主要以二进制为媒介，实现各进制之间的便捷转换，如图1 所示。

图1 各进制相互转换方法图

3.1 二进制与十进制相互转换

在这两种进制的转换过程中，我们需要熟记表2 中“2的幂”与“十进制数”的对应关系，如表2 所示。

表2 2 的幂与二进制和十进制数关系对照表

续表

3.1.1 二进制转换十进制

二进制转换十进制，由左向右从0 开始标记序号（或根据其位权幂次），忽略0 累加即可。

此方法的关键是从左侧开始数位数，忽略“0”的位数。数值大的时候，即可充分体现出此改进方法的优势。

如此，在计算时不需要写如式（1）繁杂的“1”与“0”，提高运算效率。

3.1.2 十进制转换二进制

十进制转换二进制，我们需要熟记表2 中的内容，根据需要计算的十进制数大小，进行逐值递减，具体算法[8]如下，以式（4）中的值为例。

STEP 1：判断（25）D与2n（n=1，2，3，4，…）值的大小关系

OUTPUT 1：24＜（25）D＜25

VALUE 1：24，余25-16=9

STEP 2：判断（9）D与2n的大小

OUTPUT 2：23＜（9）D＜24

VALUE 2：23，余9-8=1

STEP 3：当余值为（1）D时，OUTPUT AND VALUE：20

RETURN：24+23+20=（11001）B

注意：2n表示二进制数“1”及后面n个“0”。如24表示1 及后面0000，值（10000）B。

当需要计算的值较大时，采用如上算法，即可快速计算出结果，如计算（2023）D。

3.2 八进制、十进制与十六进制的相互转换

主要是以二进制为中介，进行快速转换。

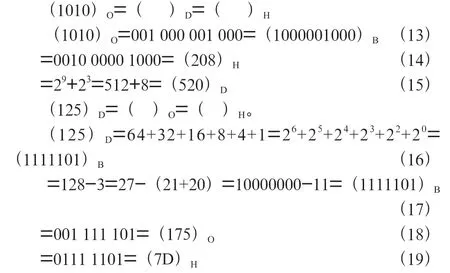
综上，改进方法重点掌握二进制与十进制的相互转换。通过以二进制为媒介，八进制、十进制与十六进制之间的相互转换，便于记忆和掌握，同时也提高了转换的速度。

4 改进方法分析

通过第1 节与第3 节对转换方法的阐述，将原转换方法与改进转换方法总结整理成对比表，便于分析和理解，如表3 所示。

表3 转换方法对比表

二进制（B）、八进制（O）与十六进制（H）的相互转换，暂无改进方法，其他进制之间的转换主要以二进制（B）为媒介。

4.1 二进制与十进制转换分析

通过表3 中第1 行、第4 行的方法对比，式（1）与式（9）计算数值一样，忽略基数为0 的位权计算，转换速度明显提高。当数值较大时，我们只需掌握表2 中“2 的幂”与“十进制数”的对应关系，甚至更大“2 的幂”的数值，即可快速计算出结果，如式（10）所示。

式（4）在短除过程中，短除5 次；式（11）中需要判断2 次（OUTPUT 1 和2），计算3 次（VALUE 1 和2，以及STEP 3），合计5 次；虽然次数差不多，但短除法更容易；我们在转换计算前，列出表2 中的对应关系，则2 次判断可以忽略，计算的速度也将大大提高。忽略判断的情况下，在式（12）中需要计算8 次；通过短除法，需要短除11 次。当需要转换的数值更大时，如（32 769）D=（ ）B，采用短除法需要短除16 次，采用改进方法只需短除2 次，即215+20。如（65 535）D=（ ）B，采用短除法需要短除16 次，采用改进方法只需短除2 次，即216-20。

综上，改进方法能有效提升二进制与十进制之间的转换速度，特别是当计算数值较大时，更能显现出其较快的转换速度。

4.2 八进制与十进制转换分析

对比式（2）与式（13）（15），式（2）中在忽略基数为0 的情况下，主要需要计算83 的值；式（13）（15）式主要是用“一位拆散位”的方法，先将八进制转换为二进制，再依据3.1.1 节的方法转换为十进制。相较于计算8 的幂，通过将八进制转换为二进制、再由二进制转换为十进制的计算难度小了很多，速度也相应提高。当计算数值变大时，效果将更加明显。

对比式（5）与式（16）/（17）+（18），采用式（5）的除基取余法需要短除3 次，采用式（16）+（18）的改进方法需要短除7 次，采用式（17）+（18）的方法需要短除4 次，短除法计算次数更少。但短除8 这样较大的数值时，在计算过程中，难免需要进行分步的计算。总体而言，改进方法更加有效、便于记忆和掌握。如4.1 节所举例的较大的数值计算时，改进方法的效果更加显著。

4.3 十六进制与十进制转换分析

与八进制转十进制一样，如式（3）中十六进制转十进制，要计算16 的幂，是比较困难的。通过式（14）+（15）以二进制为媒介的转换改进方法将更易于掌握，计算起来也更加快速。十进制转十六进制，对比式（6）与式（16）/（17）+（19），与4.2节分析一样，采用改进方法不容易出错，而且容易掌握，当计算数值较大时，转换计算速度更快。

5 结 论

本文在研究总结传统数制转换方法的基础上，提出了以二进制为媒介的数制相互转换方法，研究分析转换改进方法并证明其优势。实践表明，改进方法能够统一数制之间相互转换的计算方式，提高转换速度，易于学习和掌握，当转换计算数值较大时，其优势更加明显。下一步将探索小数部分转换方法，以及通过计算机程序算法实现常见数制之间的高效转换。