目标区域偏置扩展的RRT*路径规划算法
2022-11-19易驰伍建辉
易驰,伍建辉,2
(1.湖南理工学院,湖南 岳阳 414006;2.桂林电子科技大学,广西 桂林 541004)
0 引 言
移动机器人的路径规划,是按照一定的约束条件(如距离,安全,时效),规划出一条从起始位置到目标位置的可行路径。目前主流的路径规划算法有基于势场的人工势场法[1]、基于仿生学算法的蚁群算法[2,3]、粒子群算法[4,5]和遗传算法[6]、基于图搜索方法的A*算法[7]和Voronoi 图法[8]、基于采样方法的RRT 算法[9,10]和PRM 算法[11]。其中,RRT 算法是基于采样方法的经典代表之一,通过随机采样和碰撞检测的方法,获得一条无碰撞路径。由于RRT 算法没有考虑到路径花费的原因,往往不能得到最优路径。针对RRT 算法的这一不足,Karaman 等人[12]提出RRT*算法,在RRT 算法的基础上增加了邻节点重新选择和重连接的步骤来保证算法的渐进最优性。但是由于RRT*算法采样的随机性,导致算法对目标的导向性弱,会对一些无效的区域进行过多的探索,同时随机树中存在大量未起到优化当前路径的节点,导致收敛到最优或接进最优路径的速度慢。
如何改善RRT*算法低收敛速度的问题获得了广泛研究,Gammell 等人[13]提出Informed-RRT*算法,通过起始点、目标点和当前路径来确定椭圆采样区域,使算法减少对无效区域探索,从而加快算法的收敛速度,但是Informed-RRT*算法能够限制采样空间,但无法限制随机树的大小。Kim 等人[14]采用一种尺寸减小的方法来缩小Informed-RRT*算法的椭圆空间,提高了算法的收敛速度。Mashayekhi 等人[15]提出将RRT*-connect 算法与Informed-RRT*算法相结合,利用双向树快速找到初始路径后利用椭圆形子集采样,从而加快了算法的收敛速度。Nasir 等人[16]提出了RRT*-smart算法,通过智能采样策略来去除不必要的节点,提高了算法的收敛速度。Adiyatov[17]提出RRT*-FN 算法,通过限制节点最大数量来提高算法收敛速度。
为改善RRT*算法对目标导向性差的问题,Moses等人[18]提出目标定向的方法,通过选取一对随机采样点中更接近目标点的作为采样点,有效提升算法对目标的导向性。Noreen等人[19]提出了有界目标偏置采样的方法,通过在路径周围区域内选取采样点,从而提高算法收敛速度和对目标的导向性。刘建宇等[20]提出改进的RRT*-connect 算法,在目标偏向策略的基础上对采样区域进行约束,保证每次采样向着目标方向,从而加快算法的计算效率。
基于上述研究,本文针对RRT*算法收敛速度慢和目标导向性差的问题,提出基于目标区域偏置扩展的RRT*路径规划算法。首先对目标偏置方法进行改进,通过改变概率阈值和选取目标区域范围内的点作为目标偏置,在加强算法对目标的导向性的同时,使算法能够适应不同环境。当算法完成初始路径规划后,采用椭圆子集采样的方法缩小算法的采样空间,减少算法对无效空间的探索。其次,利用节点约束策略,计算新节点的潜在最小路径长度,并拒绝潜在最小路径长度大于当前路径长度的新节点加入随机树中,有效地减少了随机树节点数量,从而加快了算法收敛速度。最后针对路径曲折的问题,采用路径修正方法对路径进行平滑处理,得到最终可供移动机器人行驶的路径。
1 目标区域偏置扩展的RRT*路径规划算法
目标区域偏置扩展的RRT*路径规划算法主要由目标区域偏置扩展、椭圆子集采样、节点约束策略和路径修正四个部分组成
1.1 目标区域偏置扩展
本节提出目标区域偏置扩展的方法,来提高算法对目标的导向性,通过比较目标扩展概率pgoal和随机采样概率prand这两个随机数的大小,来确定采样方式。若pgoal大于prand,则随机选取以目标点zgoal为圆心,以目标点zgoal到随机树的距离为半径r 的圆内一点为采样点zrand,否则在地图中随机产生一个采样点zrand。通过这种方式使得随机树在朝向目标点方向拓展的前提下,仍保留随机树对未知区域的探索能力,能更好地适应不同环境,有效提高算法对目标的导向性。如图1 所示,为目标区域偏置扩展的示意图。

图1 目标区域偏置扩展示意图
采 样点生成公式可表示为:

完 成采样后借鉴引力场的思想,通过给采样点和目标点分配不同权重,使得每一次扩展同时由采样点和目标点共同决定,从而克服新节点扩展的盲目性。新节点生成公式可以写为
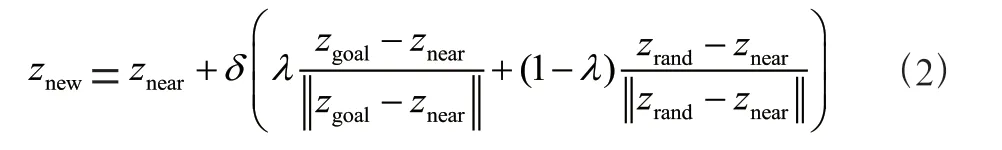
其中R 为地图尺寸大小;znear为邻近节点;zgoal和zrand分别为目标点和随机采样点;δ 为扩展步长;λ 为权重系数;ran d 为(0,1)区间均匀分布的随机函数。
1.2 椭圆空间采样
为改善 RRT*算法收敛速度慢的问题,本节通过当前路径长度、起始点和目标点生成一个椭圆空间来代替在全部状态空间进行采样。由于椭圆的几何性质,椭圆内的点到两焦点的距离和小于椭圆的长轴,所以能优化当前路径的采样点都存在于椭圆内。随着迭代次数不断增加,椭圆空间不断缩小,路径长度也不断缩短,最终得 到最优路径。如图2 所示,为椭圆空间采样的示意图。
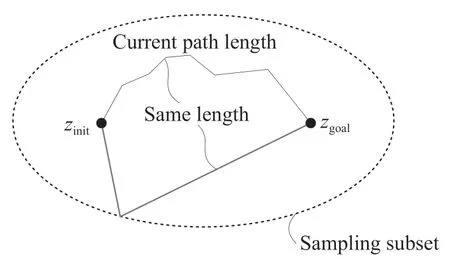
图2 椭圆子集采样示意图
假设ze是标准椭圆采样节点,L 是当前路径长度,是的x 轴坐标,是的y 轴坐标。标准椭圆采样节点定义为

椭圆子集采样节点zerand由标准椭圆采样节点ze旋转和平移来确定,因此椭圆子集采样节点zerand可以表示为

其中α 是连接起始节点和目标节点的直线与x 轴的夹角。
1.3 节点约束 策略
为了减少需要添加到随机树中的无效节点数量,本节提出节点约束策略,通过比较新节点znew的潜在最小路径成本F 与当前路径长度L,来判断该节点是否具备优化当前路径的能力。潜在最小路径成本F 为邻节点znear回溯到起始点zinit的路径长度g(znear),加上新节点znew到邻节点znear的直线距离d(znew,znear),再加上新节点znew邻近区域内的当前路径点到目标点的路径长度的最小值fmin(znew)。若潜在最小路径成本F 大于当前路径长度L,则新节点znew不参与后续一系列的步骤。图3 为潜在最小路径成本示意图,图中绿色虚线为新节点znew最小路径成本F。

图3 潜在最小路径 成本示意图
潜在最小路径成本F 的计算公式可表示为
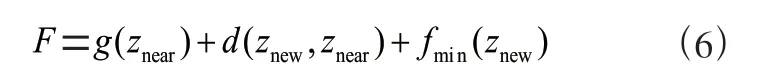
1.4 路径修正
本节采用逆 向寻优和路径 平滑的方法对规划得出的路径进行优化和平滑处理。优化过程为:首先判断zinit与zgoal之间是否存在障碍物,若不存在,则将zinit作为zgoal的父节点;若存在障碍物,则判断zgoal的父节点与zinit之间是否存在障碍物,并重复上述过程直到找到与zinit之间不存在障碍物的路径点为止。得到与目标点zinit之间没有障碍物的路径点后,以该路径点作为下一步逆向寻优的起点,并重复上诉步骤直到完成整条路径的寻优。图4 为路径逆向寻优示意图。
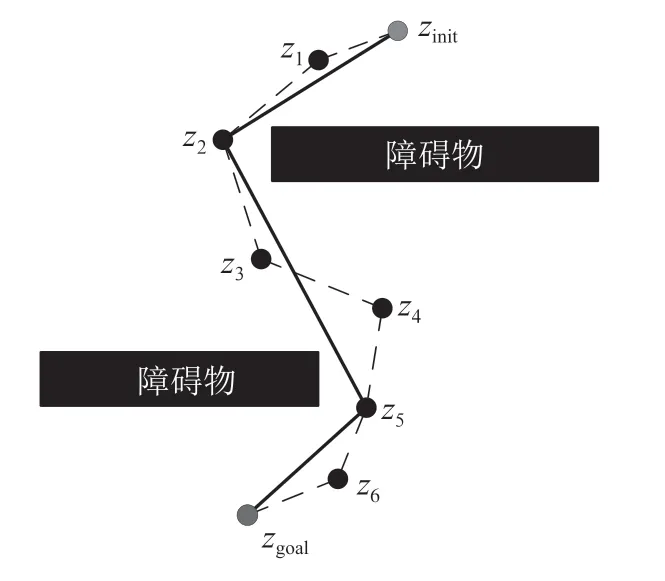
图4 路径逆向寻优示意图
三次B 样条曲线用于平滑路径,3 次B 样条曲线的基函数可表示为

3 次B 样条曲线和控制点之间的关系可以表示为
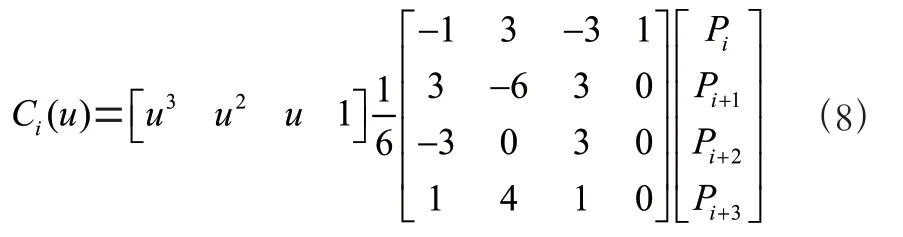
其中Pi、Pi+1、Pi+2 和Pi+3 为路径控制点。
2 算法实现
基于目标区域偏置扩展的RRT*路径规划算法实现的具体步骤描述如下:
Step1:初始化随机树,确定起始节点和目标节点。
Step2:迭代开始,如果算法没有搜索到初始路径,则进入Step3;否则,进入Step4。
Step3:在(0,1)区间随机生成采样概率prand和目标扩展概率pgoal,若prand<pgoal则在目标区域内进行采样;否则,使用全局均匀采样。进入Step5。
Step4:在以初始路径长度为长轴,以起始点和目标点为焦点的椭圆区域内进行采样,并对执行节点约束策略,若满足节点约束条件进入Step5;否则回到Step2。
Step5:选择采样点距离随机树中最近的节点作为邻节点znear,并通过目标扩展生成新节点znew。
Step6:检查新节点与邻节点之间的路径是否与障碍物发生冲突,如果没有冲突则进入Step7;反之,回到Step2重新进行采样。
Step7:在新节点znew 的邻近区域内重新选择父节点,使得新节点znew到起始点的路径长度能够最小,并将新节znew点插入到树中。
Step8:在新节点znew邻近区域内执行重连接策略,使邻近区域内所有节点到起始点的路径长度最小。
Step9:检查新节点是否在目标区域内,如果新节点在目标区域内,则生成一条初始路径,回到Step2;若达到设定迭代次数则退出程序,输出最优路径坐标点。
路径修正实现的具体步骤描述如下:
Step1:通过逆向寻优得到新的路径点坐标。初始化曲线公式的各项参数。
Step2:将逆向寻优得出的路径坐标作为曲线的控制点。
Step3:通过公式(7)得到3 次曲线方程基函数。
Step4:将控制点坐标和3 次曲线方程基函数带入公式(8)得到优化后的路径坐标,最后依次连接3 次曲线得到最终路径。
3 算例仿真及分析
本节通过如图5 所示的两种不同 地图环境,对本文所提算法、RRT*[12]、Informed-RRT*[13]和RRT*-FN[17]算法进行仿真实验,通过对比初始路径规划结果和算法收敛所花费时间来验证本文算法的有效性。其中图5(a)为简单地图环境,大小为800×800,图5(b)为复杂地图环境,大小为1 000×1 000。每种算法都进行300 次仿真实验以减小实验的随机性。算法仿真的软件为64 位MATLAB 2018b,硬件条件为Intel® CoreTM i7-10700 CPU@2.90 GHz,内存为8 GB。

图5 地图环境图
3.1 简单地图环境
本节将验 证本文算法在简单地图环境中的有效性,并将其与其他三类算法进行对比。路径规划的起始点坐标为[10,10],目标点坐标为[790,790]。如图6 所示,为4 种路径规划算法在简单地图环境的初始路径规划图。对比图6(a)(b)(c),可发现本文所提算法对无效区域的探索较少,扩展节点少,初始路径平滑。
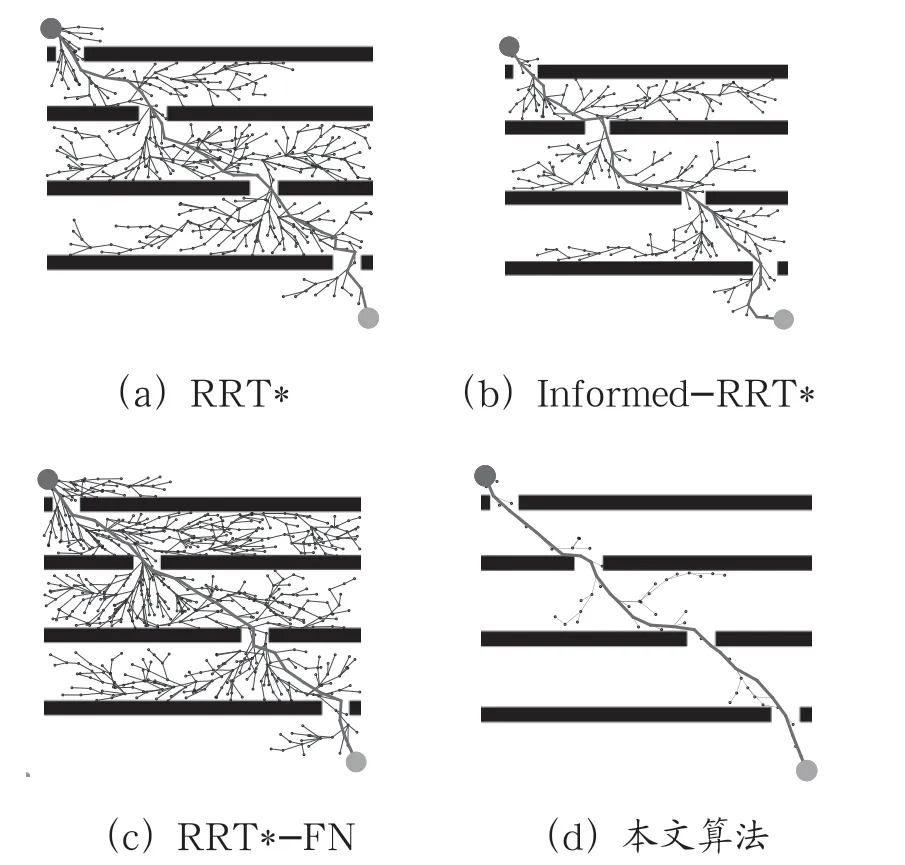
图6 简单地图环境下4 种算法的初始路径 规划图
如表1 所示,为简单地图环境下4 种算法的初始路径规划结果。由表1 可知,本文提出的算法初始解的平均路径长度Lc有一定的提升,在扩展节点数量Sc上相对RRT*、Informed-RRT*和RRT*-FN 算法分别减少了71.7%、72.1%和71.2%,初始路径规划时间Tc分别减少了80.0%、80.3%和80.6%,这也从侧面反映本算法能有效提升目标导向性。

表1 简单地图环境下4 种算法的初始路径规划结果
如图7 所示,为简单地图环境下4 种算法收敛后的路径规划图。由图7 可发现上述4 种算法在简单地图环境下都能找到渐进最优路径。与RRT*、Informed-RRT*和RRT*-FN三类算法相比,本算法的扩展节点数量较少,这也能说明椭圆子集采样和节点约束策略能有效地减少扩展节点的数量。
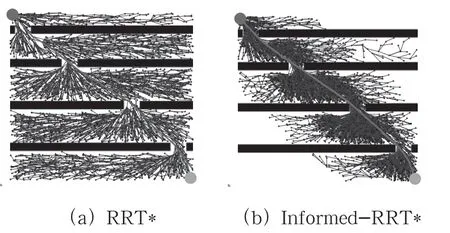
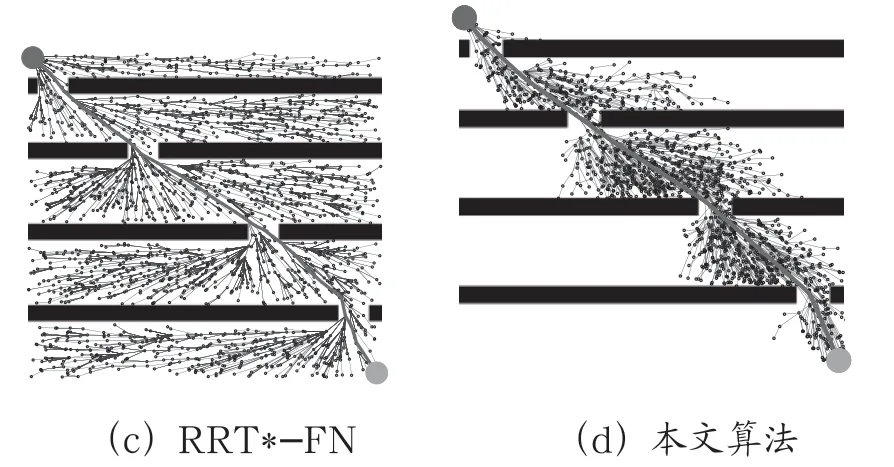
图7 简单地图环境下4 种算法收敛后的路径规划图
如表2 所示,为简单地图环境下4 种算法收敛后的结果。由表2 可知,在路径长度上本算法与其他3 类算法近似。相对其他3 类算法,本算法在收敛时间上分别减少了69.3%、74.6%和56.2%,这也从侧面反映本算法能提高收敛速度。

表2 简单地图环境下4 种算法收敛后的结果
如图8 所示,为简单地图环境下路径修正前后对比图。由图8 可知,路径进行修正后,变得比较平滑,一些小折角也被消除,且路径的大体趋势几乎没有改变。

图8 简单地图环境下路径修正前后对比图
3.2 复杂地图环境
本节将验证本文算法在复杂地图环境中的有效性,并将其与其他三类算法进行对比。路径规划的起始点坐标为[10,10],目标点坐标为[900,900]。如图9 所示,为复杂地图环境下4 种算法的初始路径规划图。对比图7(a)(b)(c),可发现本文算法对无效区域的探索较少,路径长度更优。以上说明了目标区域偏置扩展能有效提高算法对目标导向性。

图9 复杂地图环境下4 种算法的初始路径规划图
如表3 所示,为复杂地图环境下4 种算法的初始路径规划结果。由表3 可知,本文算法在扩展节点数量Sc上相对RRT*、Informed-RRT*和RRT*-FN 算法分别减小了63.3%、63.7%和64.4%,初始路径规划时间Tc分别减少了71.6%、71.3%和70.8%,这也表明了本文算法能有效提高目标导向性,更快规划出一条初始路径。
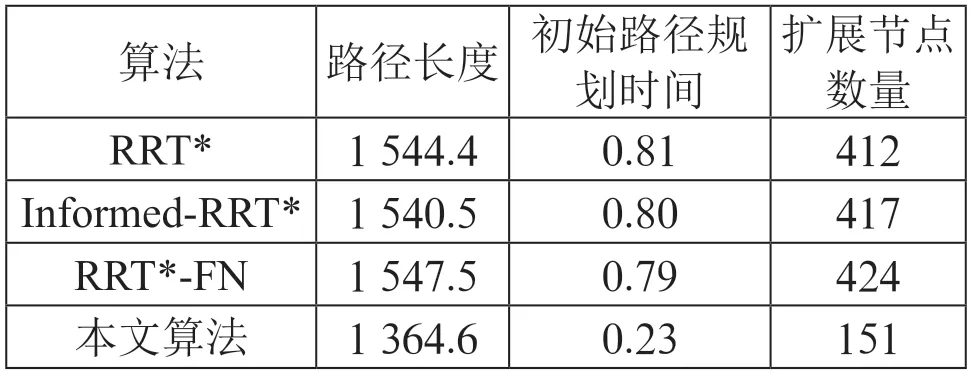
表3 复杂地图环境下4 种算法的初始路径规划结果
如图10 所示,为简单地图环境下4 种算法收敛后的路径规划图。由图10 可发现与RRT*、Informed-RRT*和RRT*-FN 算法相比,本算法有效限制了采样空间大小和采样节点数量,且路径长度相对于其他3 类算法更加平滑,这说明椭圆子集采样和节点约束策略能有效地减少扩展节点的数量。
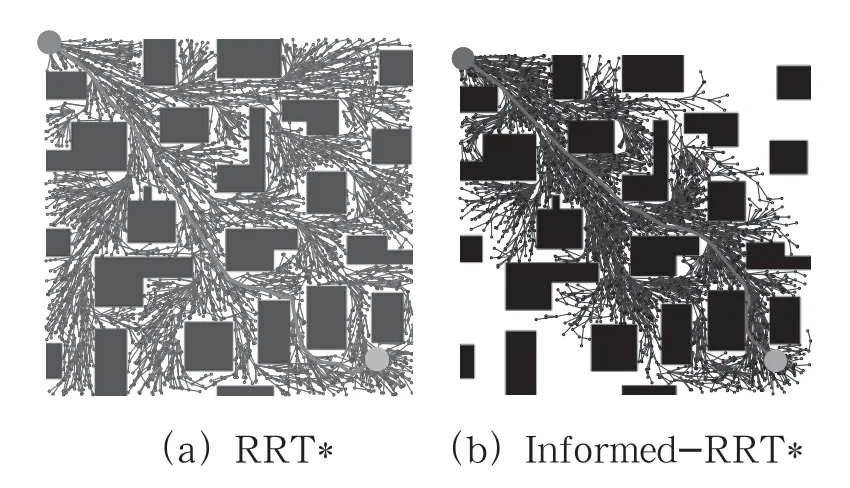
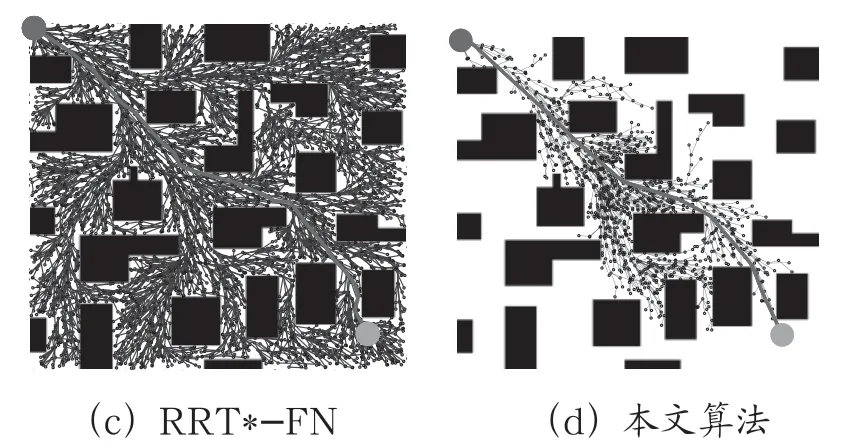
图10 简单地图环境下4 种算法收敛后的路径规划图
如表4 所示,为复杂地图环境下4 种算法收敛后的结果。由表2 可知,在路径长度Ls上本算法与其他3 类算法近似。相对于其他3 类算法,本算法在收敛时间Ts上分别减少了70.9%、68.6%和43.8%,表明本文算法能提高收敛速度。

表4 复杂地图环境下4 种算法收敛后的结果
如图11 所示,为复杂地图环境下路径修正前后对比图。由图11 可知,在复杂环境中路径修正方法同样能在不改变路径整体趋势的前提下,对路径进行平滑处理。

图11 复杂地图环境下路径修正前后对比图
4 结 论
本文针对RRT*路径规划算法目标导向性弱和收敛速度低,提出了基于目标区域偏置和扩展的RRT*路径规划方法,并给出了算法的实现过程。仿真结果验证了所提算法的有效性,并显示了RRT*、Informed-RRT*、RRT*-FN 和本文算法在两种不同环境下的结果。结果表明,本文算法可以增强目标导向性,有效减少采样节点数,加快算法的收敛速度。此外,本文算法使规划的路径更加平滑。
