无高斯采样的层级多身份全同态加密方案

侯凌云

(广西大学 计算机与电子信息学院，广西 南宁 530004)

0 引 言

身份加密（Identity-Based Encryption, IBE）体制是一种不需要申请公钥证书认证用户身份的密码体制，于1984年由Shamir[1]提出，该体制在解决云上全同态计算时的身份认证问题上有着天然的优势。层级IBE 体制(Hierarchical IBE,HIBE)作为一种衍生体制解决了原始体制中因用户增多导致私钥派发负担过重的问题。自2013年学者Gentry[2]提出了首个基于层级IBE 的全同态加密方案(Hierarchical Identity-Based fully homomorphic encryption, HIBFHE)后，格上基于身份的全同态方案逐渐成为研究热点。

2015年，Clear[3]等人针对文献[2]仅满足单一身份设置的同态计算，提出了格上首个多身份的全同态加密方 案(multi-Identity Based fully homomorphic encryption,mIBFHE)，该方案也被称为CM15 方案。2016年，针对CM15 方案MS 系统扩展规则烦琐低效的问题，Mukherjee等人[4]对CM15 方案中的矩阵扩展操作进行了简化。此后，多位学者基于不同的身份加密框架对前者的工作做出了优化[5-7]，但这些方案均构建在LWE 困难假设上，在加密阶段需要大量的高斯采样，进而影响方案效率。LWR 困难假设是一种不需要高斯采样的假设，通过舍入函数隐藏明文信息，其概念于2012年由Banerjee[8]等人提出，是LWE 困难假设的一个变体。2016年Bogdanov[9]等人证明模q为多项式时的情况下LWR 问题的难解度可以归约至LWE 问题。2017年，Costache[10]等人基于LWR 的困难假设构造了一个全同态加密方案，由于LWR 问题涉及两个不同的模数且该方案采用张量积实现同态乘法，导致方案存在模数纠缠的问题。2018年，Luo[11]等人受到Costache 等人工作的启发，采用文献[2]中提出的近似特征向量方法构造全同态加密方案，消除了模数纠缠的问题，并将方案扩展至多密钥设置。同年，卢玉顺[12]利用多线性映射的不可区分性混淆器以及可穿孔伪随机函数构造了一个基于LWR 的mFHE 方案和一个属性FHE 方案。

基于同类方案存在加密阶段存在频繁高斯采样导致效率低下且同态计算时多身份扩展规则复杂的问题，本文提出了一个无高斯采样的层级多身份全同态加密方案，主要贡献如下：

（1）利用舍入函数和模p上的工具矩阵 ，对原始方案的中的噪音采样进行了消除，通过近似特征向量的思想消除了两个不同模数之间的纠缠问题，密文扩展率由logq降低到logp。

（2）针对第一个方案中扩展框架复杂及操作烦琐的问题提出了一个LComb 算法，利用该算法构建了一个全新的LWRMask 系统，将方案从单一身份扩展到多身份的同态计算。

1 基础知识

1.1 相关数学问题

定义1：LWR 问题。n和m为选取的正整数，p，q为模数且，给定从分布，上选取的秘密向量s∈，令舍入函数为为满足的任意整数，表示x在舍入函数计算后从Zq到Zp的缩减。定义LWR 分布表示一个LWR 实例。

判定性DLWR 问题是指：在m个采样中区分其属于LWRn，q，p（D）分布还是属于真均匀随机分布

1.2 IBE 相关算法及引理

引理1-1[4]：对于任意的存在一个可计算的有效矩阵和一个可计算的确定性逆向函数G-1(·)，输入矩阵，逆向函数G-1(M)输出一个元素分量仅为0 和1 的扩展矩阵其满足GG-1(M)=M。

定理1-1[9]：（LWR 的困难性）对于正整数m，n以及模数p，q，且q＞2mpB若存在一个算法使得：其中A为一个随机均匀的矩阵，s为一个随机选取的n维0/1 向量，为上的随机均匀向量，则存在一个在m，n以及q的除因子数的多项式时间中运行的算法 ，满足：噪音e在空间坐标中是B为有界和均匀分布的，且满足

2 方案构造

2.1 LWR-Mask 系统

本节通过构造一个LWR-Mask 系统实现多身份间的同态计算，以参与计算方party1，party2 为例展示单一身份至多身份的扩展过程。令与分别为两个身份参与方对应的私钥，为两方私钥的级联向量，令为扩展后的模p上的工具矩阵，分别为party1，party2 的扩展密文，实现一个LWR-Mask系统的关键技术在于需要生成一个特殊的矩阵X，使得即扩展后的密文在进行同态计算后得到的结果仍满足保持同态解密的正确性。LWR-Mask 系统的构造分为两个过程，首先通过构造一个LComb 算法生成特殊矩阵X。随后，利用特殊矩阵X对不同参与方的密文矩阵进行扩展，扩展后的密文满足

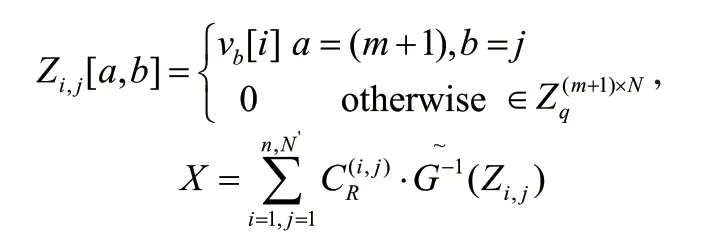
则有：

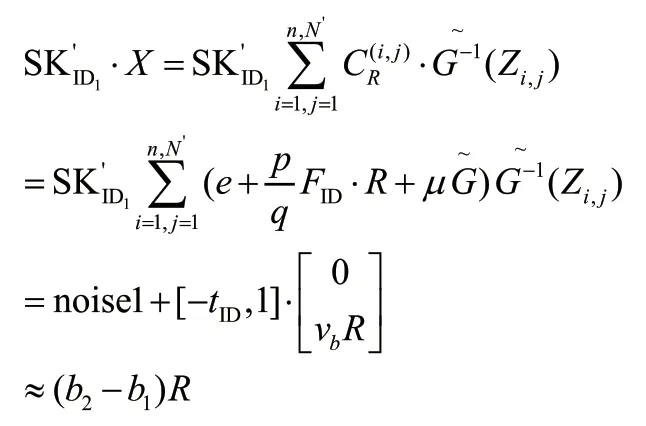
扩展规则：LWR-Mask（ID1，ID2，μ1）输入参与方身份ID1，ID2，LWR-Mask 系统对身份IDi，i∈[1，2]密文的构造分为加密阶段和扩展阶段：

2.2 基于LWR 的mHIBFHE 方案构造

基于2.1 节构造的LWR-Mask 系统，本节构造了一个基于LWR 的无高斯采样层级多身份全同态加密方案，方案的涉及的基本参数包括：m=m（λ, depth, L）=O（nlogp+nlogn），n=n(λ, depth,L)，q＞2mpB，令工具矩阵：

mHIBFHE.Setup(1λ,1depth) 输入安全参数λ以及HIBE 系统的最大层级深度depth，调用文献[13]的算法生成随机均匀矩阵为可逆矩阵，以及A0的陷门矩阵，选取随机均匀向量，输出主公钥

mHIBFHE.KeyGen(params, IDK, IDK-1)输入系统公共参数及父级、子级身份信息，首先调用文献[14]的Extract 算法，生成父级身份的加密矩阵以及对应的陷门其次调用文献[14]的Derive 算法，生成IDK-1的子级身份IDK的陷门矩阵，计算输出：

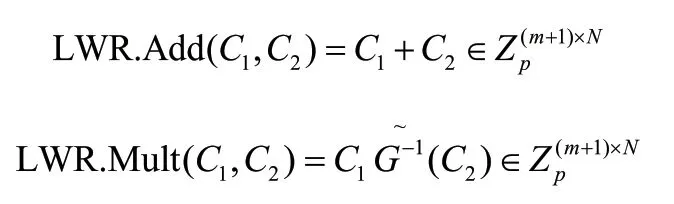
mHIBFHE.Extend((ID1, …, IDK,…, IDd),CK,RK)，CK表示在身份IDK下计算得到的密文，RK为对应的随机{0，1}矩阵，R[i,j]{i∈[n]，j∈[N´]}代表随机矩阵中第i行第j列的元素，令为在IDK的公钥下对R[i,j]的加密结果，调用LWR-Mask.Enc 算法生成：调用LWR-Mask.Expand 算法输出CK的扩展矩阵。

3 方案分析

3.1 方案正确性分析

3.2 方案安全性分析

安全性本文方案采用舍入函数隐藏明文信息，其安全性基于定理1-1、定理3-1、定理3-2。

定理3-1：在随机预言模型中, 令Adv 为一个具有INDr-ID-CPA 优势的攻击者，QH为攻击者向随机预言机进行哈希查询的次数，depth 为本文方案的身份分级层数，若攻击者Adv 具有INDr-ID-CPA 优势，则存在一个优势为ε的PPT 算法求解DLWR 问题，且

定理3-2：若LWR 假设的困难性成立，则本文提出的LWR-HIBFHE 方案满足随机预言模型下的INDr-ID-CPA 安全。

Queries1：攻击者Adv 可以自适应的询问随机预言机任意身份信息，对于Adv 针对身份信息IDl=（id1, …,idl）（l ≤depth）的询问，令j=∈[l]为本文身份加密系统的最低分级深度，算法作如下回答：

（1）若ID*未被Adv 询问，设j=1。

（2）假设对任意身份的ID 进行查询前是对其每个身份位的哈希查询，询问随机预言机H 每个身份位idi对应的结果并构造可逆矩阵←H（l，idl）…H（2，id2）H（1，id1），一般性认为在询问H（l，idl）时，其前缀均被询问完毕；若有H（idj）=R*j，则终止询问。构造矩阵B=A•（R*1）-1…（R*j-1）-1•H（j，idj）-1；已知TB是矩阵B的陷门，矩阵B的构造与本文方案中的身份加密矩阵构造相同，不难得出，TB为其陷门。

（4）输入子级身份对应的陷门,调用文献[13]算法MP12SampleD 生成子级身份的私钥并发送给攻击者Adv。

Challenge：Adv 宣布将要挑战的目标身份ID*，并将明文μ*∈{0,1}发送给挑战者，其中在任何之前及后续的查询过程中，ID*限制为不能等于任何已进行查询的身份信息或其子级身份信息。对于目标身份ID*，算法执行如下操作：

（2）计算C1←mHIBFHE.Enc（ID*，μ*）

挑战者选择比特值b*∈{0,1}，若b*=0 则将C0发送给敌手；若b*=1 将C1发送给敌手。

Queries2：攻击者Adv 以Queries1 阶段查询的方式再次向询问一定数量的身份对应的私钥信息，其中ID ≠ID*。

Guess：攻击者Adv 根据训练猜测挑战密文是否由算法mHIBFHE.Enc 生成，若是，则输出猜测结果b*=1；

否则输出结果b*=0。算法根据Adv 的猜测输出判定结果并结束模拟游戏。

3.3 方案效率分析

由表1 可知，本文构造的基于LWR 的mHIBFHE 方案在主私钥尺寸上有明显缩减，消除了烦琐的高斯采样，保持了密文尺寸的优势，提升了加密阶段的效率。并利用本文构建的LWR-Mask 系统下完成了单一身份至多身份的扩展，只需构建一个特殊矩阵X即可完成密文扩展，扩展规则相比CM15 方案有较大简化，且可以实现多用户之间的联合同态计算，是更为高效的多身份全同态加密方案。

表1 本文LWR-mHIBFHE 方案与同类方案对比

4 结 论

本文在研究分析了以CM15 方案为蓝本的多身份基全同态加密方案后，从缩减公钥尺寸、简化掩蔽系统、减少高斯采样这几个角度出发构造了一个基于LWR 的无高斯采样的多身份全同态加密方案，将方案的主私钥尺寸从m×m缩减至m×m/4，且去除了高斯采样，其密文扩展率也由logq降低到了logp级别。但本文方案仅满足对单比特的明文加密，如何构造一个多比特的方案是进一步需要深入研究的问题。