一种新的高精度光纤平台系统级标定方法

张 文，王庭军，王 雷，陶 陶

(中国航天科技集团公司 第九研究院 第16研究所, 陕西 西安 710000)

0 引言

光纤平台具有高精度、数字化、启动时间短等优点，是当前高精度惯性平台系统的又一发展方向[1-2]。与传统的机械陀螺平台系统不同，光纤平台系统存在杆臂、时间不同步等误差，所以需要研究新方法进行标定。

高精度光纤平台系统的输出为数字量,且误差与重力加速度g无关。因此，采用连续旋转自标定的系统级标定法可完成误差参数的标定[3-4]。连续旋转自标定以当地的g和地球自转角速度作为基准，通过框架系统使平台按照提前设定的轨迹连续旋转，对翻滚过程中陀螺仪与加速度计的输出数据进行采样，选取Kalman滤波等参数估计方法完成系统误差标定[5]。文献[6]讨论了一种可激励出51项误差的惯性平台系统十六位置自标定方案，但仍要依赖于精密转台完成标定。文献[7]虽然验证了转台转位误差、速率误差和不正交度对标定结果的影响，建立了以速度误差为观测量的30维Kalman滤波模型，但惯性器件的误差模型较简单。文献[8]介绍了捷联惯导系统杆臂效应的一种分立式标定方法，标定结果的重复性较好，但仍受到转台精度的影响。文献[9-13]给出了杆臂误差及时间不同步误差的误差模型，论证了对惯导系统的杆臂误差及时间不同步误差进行误差标定与补偿，以及对提高惯导系统级标定精度的必要性。文献[14]通过对比分析分立式标定和系统级标定的结果，给出了34维Kalman滤波误差模型，有效地提高了惯导系统在动态环境中的导航精度。

针对高精度光纤平台系统级标定技术问题，本文通过分析光纤平台系统的误差特点，提出了一种平台锁定回路状态下两级系统级标定方法。一级标定包含了通用误差参数、杆臂误差及时间不同步误差，对标定出的杆臂误差及时间不同步误差进行离线补偿。二级标定为平台的在线应用标定，仅标定通用误差参数，加快系统的标定速度。根据光纤平台系统的误差模型建立了两级标定的Kalman滤波器，利用文中给出的十九位置标定路径编排充分激励系统误差，最后对该系统级标定方法进行了仿真分析和实验验证。结果表明，采用两级标定的光纤平台系统,其误差参数辨识精度满足系统高精度的应用需求，且系统应用时的标定时间较短。

1 光纤平台系统误差模型

光纤平台惯导系统中光纤陀螺的误差模型：

(1)

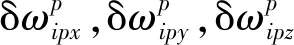
考虑杆臂效应影响的加速度计误差模型：

(2)

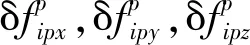
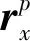
(3)

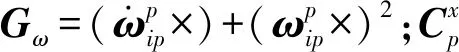
同理可得加速度计Ay、Az对应的杆臂误差为

(4)

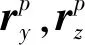
将3个加速度计杆臂误差的模型合在一起的矢量形式为

(5)

由式(2)、(5)可知，基于n系的光纤平台速度更新误差模型：

(6)

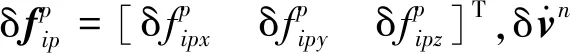
(7)

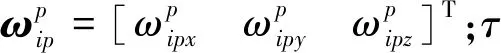
姿态更新误差模型为

(8)

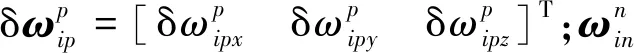
2 标定方案设计

为了能够充分激励出光纤平台系统的误差，本文采用“静止-转动-静止”的方式完成十九位置标定。初始位置的台体系指向天东北(其中，xp轴对应天向,yp轴对应台体轴,zp轴对应外框架轴)，在第一个位置静止140 s后按照表1所示方向转动30 s到达第二个位置；静止140 s后再转动到下一位置，直至第十九个位置静止140 s后关闭系统。利用连续采集到的十九位置“静止-转动-静止”陀螺仪与加速度计的脉冲数据完成光纤平台的系统级标定。

表1 十九位置标定路径编排

3 系统级标定Kalman滤波方程设计

3.1 Kalman滤波方程

为了使标定算法不依赖于高精度转台提供的姿态信息，同时在实验过程中光纤平台的速度和位置未发生变化，因此选用速度误差作为系统的观测量。系统的Kalman滤波方程为

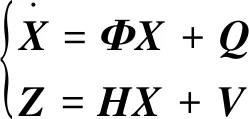
(9)

式中：X为状态向量；Z为量测向量；Φ为系统的一步状态转移矩阵；H为量测矩阵；Q,V分别为系统噪声及量测噪声。

3.2 两级标定Kalman滤波方程

光纤平台系统进行连续翻滚自标定时，杆臂误差与时间不同步误差会影响其他误差参数的辨识。考虑到杆臂误差与时间不同步误差较稳定，不易受系统温度等环境因素的影响而产生变化，为了提高光纤平台系统的应用精度，同时缩短标定时间，采取两级标定的策略实现光纤平台系统的标定。其中，第一级标定在系统上电稳定的状态进行，误差参数标定全面，获取杆臂误差及时间不同步误差值，烧写进系统中并进行离线补偿。第二级标定为平台在线应用时的标定，采用的误差模型为补偿杆臂误差及时间不同步误差后的简化模型，从而达到提高光纤平台系统级标定快速性的目的。

3.2.1 一级标定Kalman滤波方程

选取状态变量时，除姿态误差和速度误差外，还考虑了惯性仪表的零偏、标定因数误差、安装误差、加速度计的杆臂误差和时间不同步误差。系统级标定时40维的误差状态向量X1为

X1=[φnδvnεb∇bδExEzyEyzEzx

δEyExzEyxExyδEzδKxKzy

KyzKzxδKyKxzKyxKxyδKz

(10)

由式(7)、(8)可知，系统的一步状态转移矩阵Φ1为

(11)

(12)

(13)

(14)

(15)

(16)

(17)

量测矩阵H1为

(18)

3.2.2 二级标定Kalman滤波方程

经过一级标定后，误差模型得到简化，仅需考虑惯性仪表的零偏、标定因数误差及安装误差，降维后的状态向量X2为30维。光纤平台应用层级的系统级标定Kalman滤波方程为

X2=[φnδvnεb∇bδExEzyEyz

EzxδEyExzEyxExyδEzδKx

KzyKyzKzxδKyKxzKyxKxy

δKz]T

(19)

系统的一步状态转移矩阵Φ2为

(20)

量测矩阵H2为

(21)

4 仿真研究

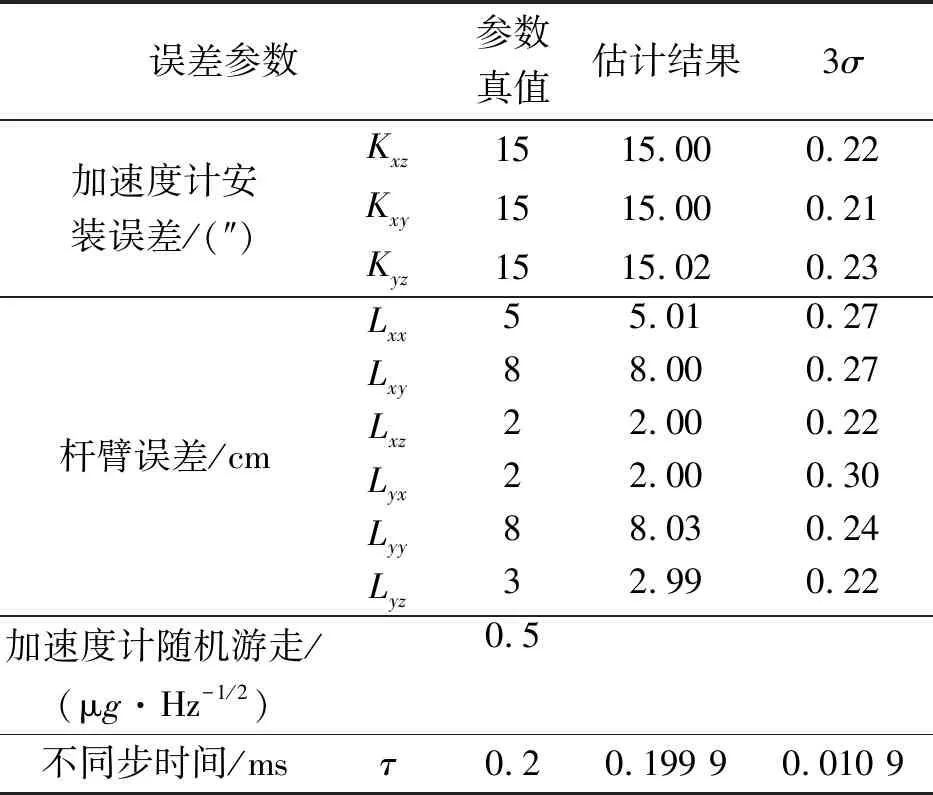
由于两级标定所采用的标定路径及误差激励方式相同，若误差参数更全面的一级40维Kalman滤波器能收敛，则二级30维Kalman滤波器也一定能收敛。因此，在设计仿真试验时仅需按照第3节内容设计一个40维的Kalman滤波器进行验证。参照实验室高精度光纤平台系统，选取表1的标定路径模拟生成陀螺仪角增量数据和加速度增量数据。仿真参数设置及经过100次蒙特卡洛仿真的结果如表2所示。

表2 参数设置及仿真结果

续表

由表2可知，光纤陀螺零偏的估计精度优于0.000 7 (°)/h，标度因数误差的估计精度优于1×10-6，安装误差估计精度优于0.3″。加速度计零偏的估计精度优于1 μg，标度因数误差的估计精度优于0.03×10-6，安装误差估计精度优于0.3″，杆臂误差估计精度优于0.3 cm，时间不同步误差估计精度优于0.02 ms。从参数估计结果可看出，光纤平台的28项误差参数估计精度较高，满足高精度惯导的标定要求。

按照表1中的转位次序进行翻滚时，俯仰角θ、横滚角γ和航向角ψ的角度变化曲线如图1所示。

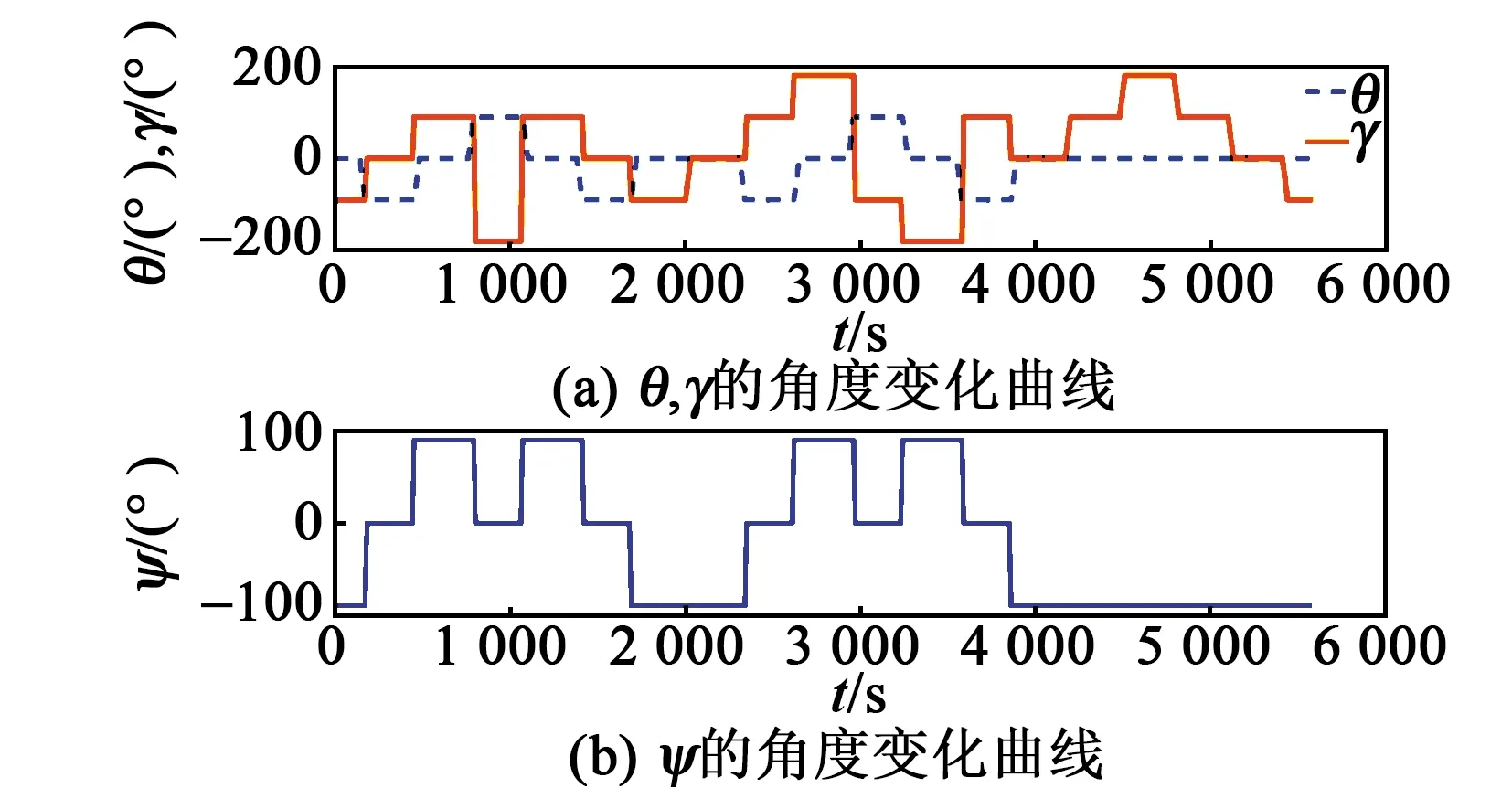
图1 姿态角变化曲线

各误差系数的仿真收敛结果如图2～9所示，完成最后一次迭代后，各误差项已收敛至0，实现了系统误差参数的辨识。

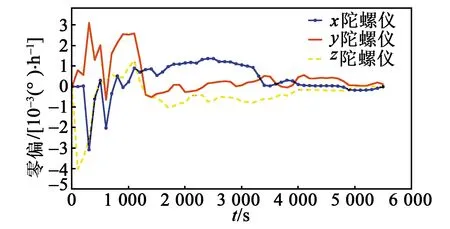
图2 陀螺仪零偏

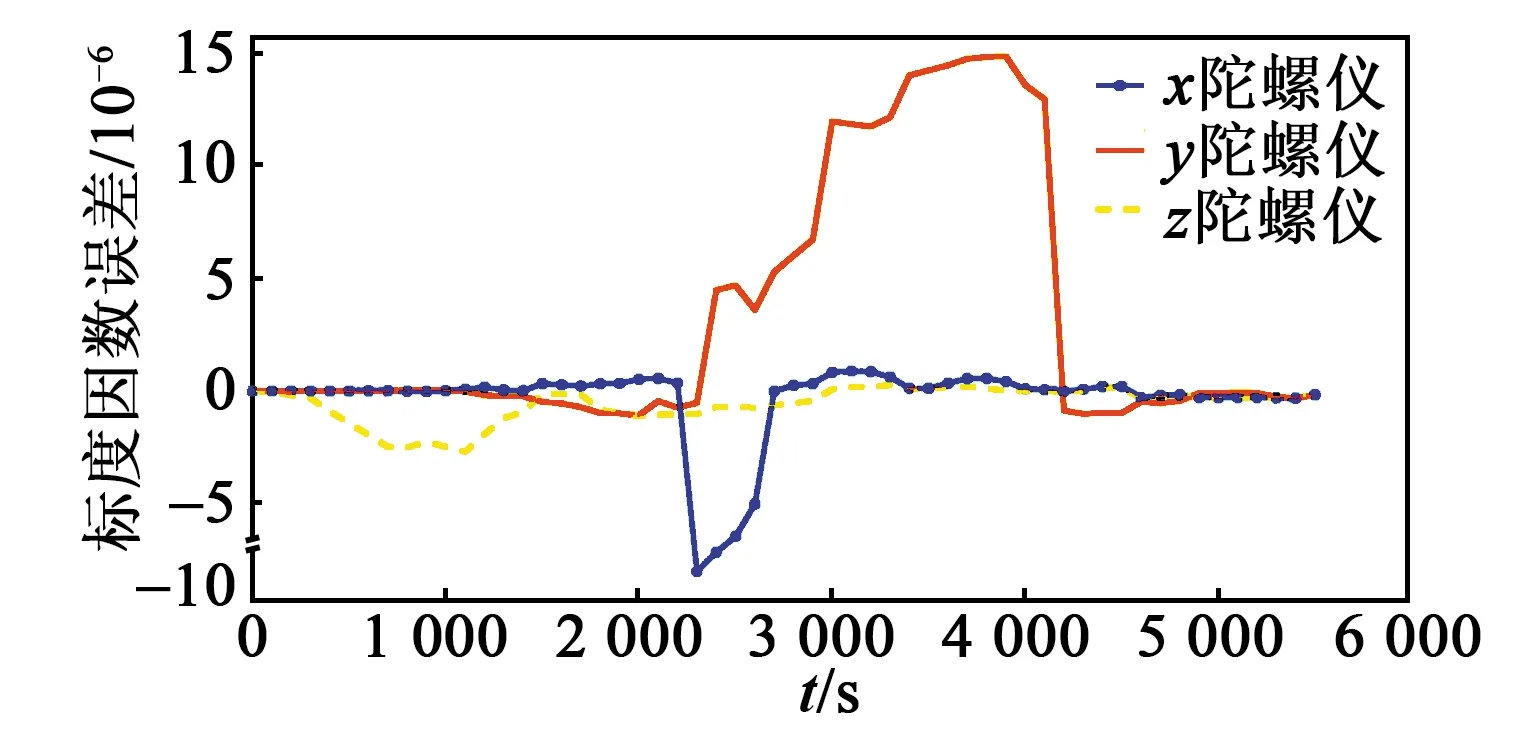
图3 陀螺仪标度因数误差

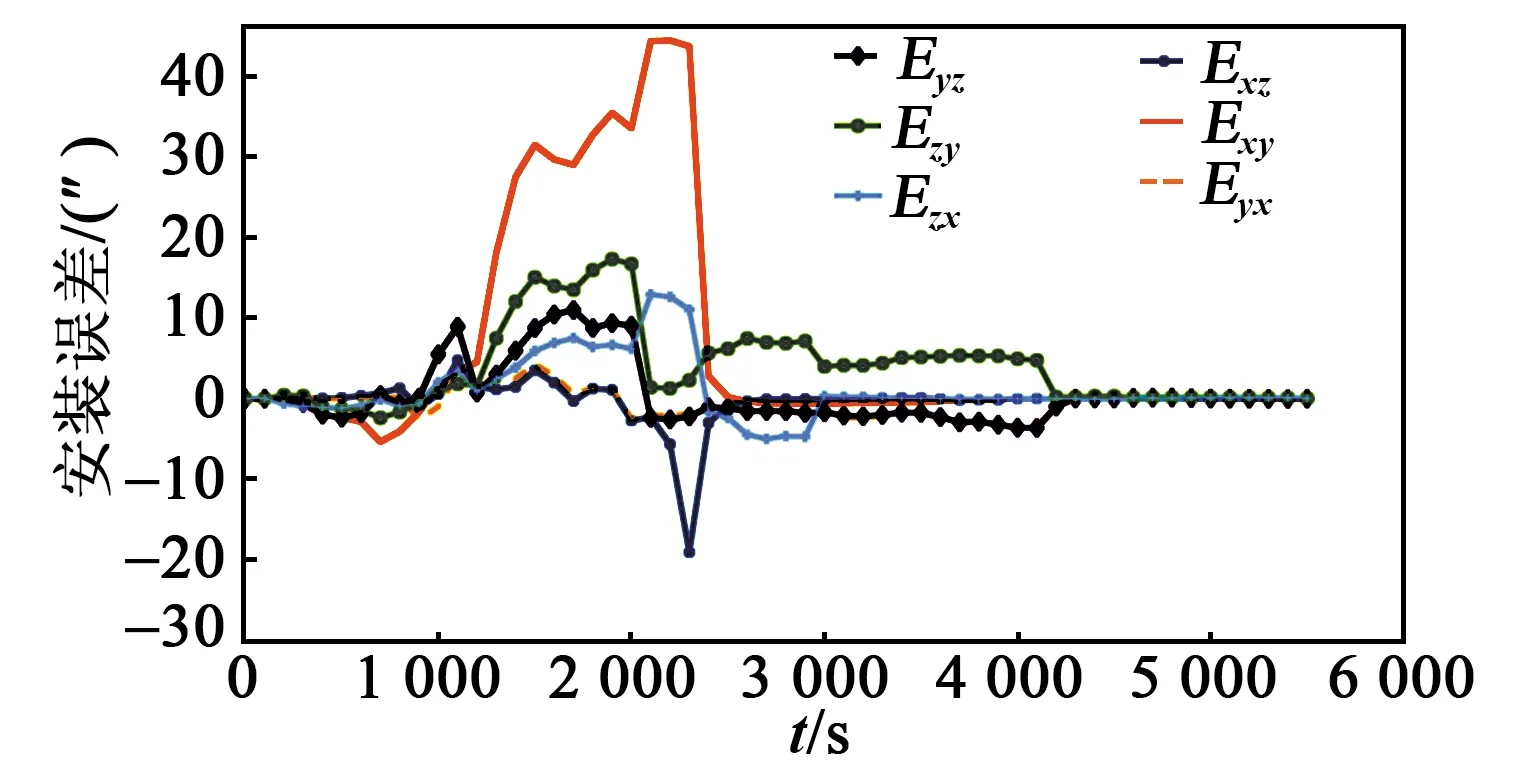
图4 陀螺仪安装误差

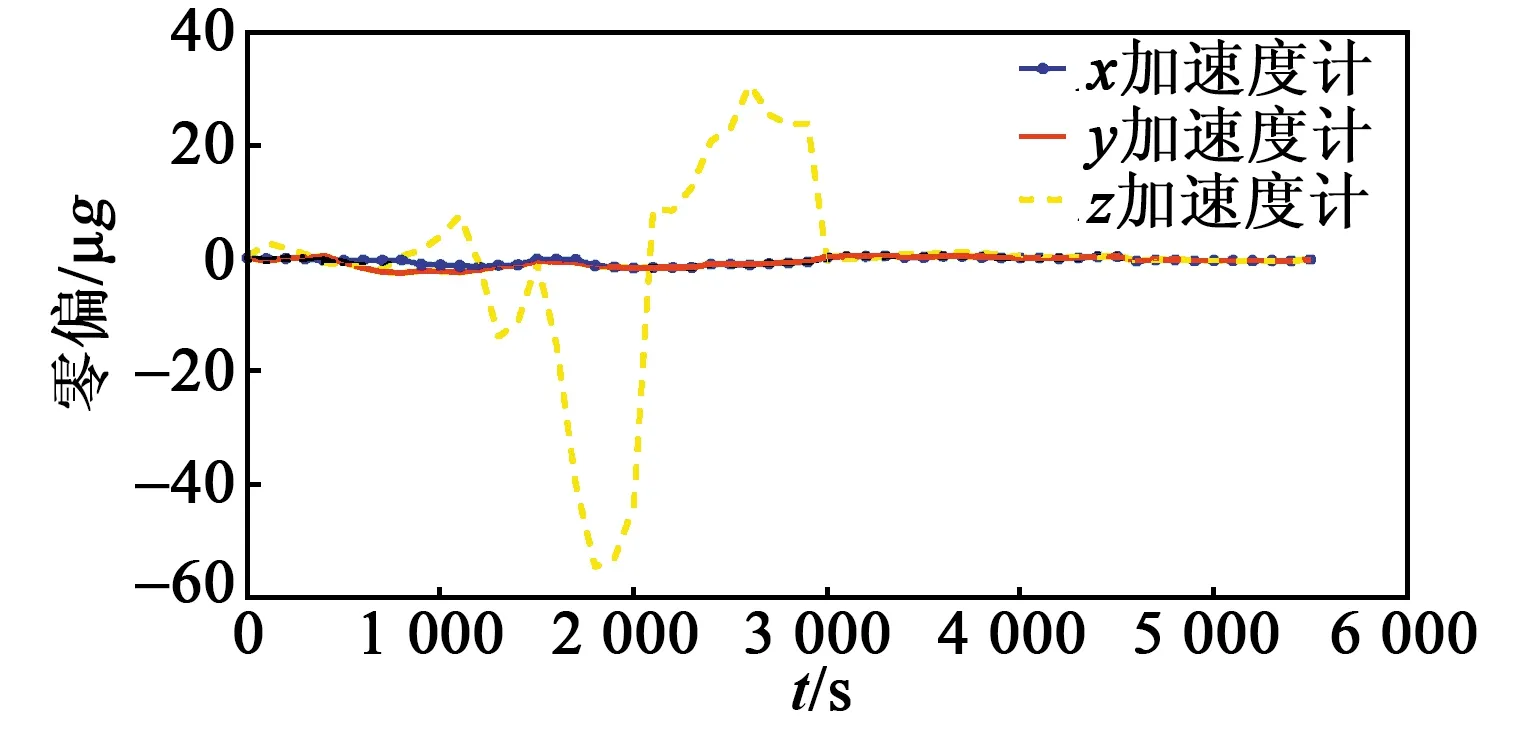
图5 加速度计零偏

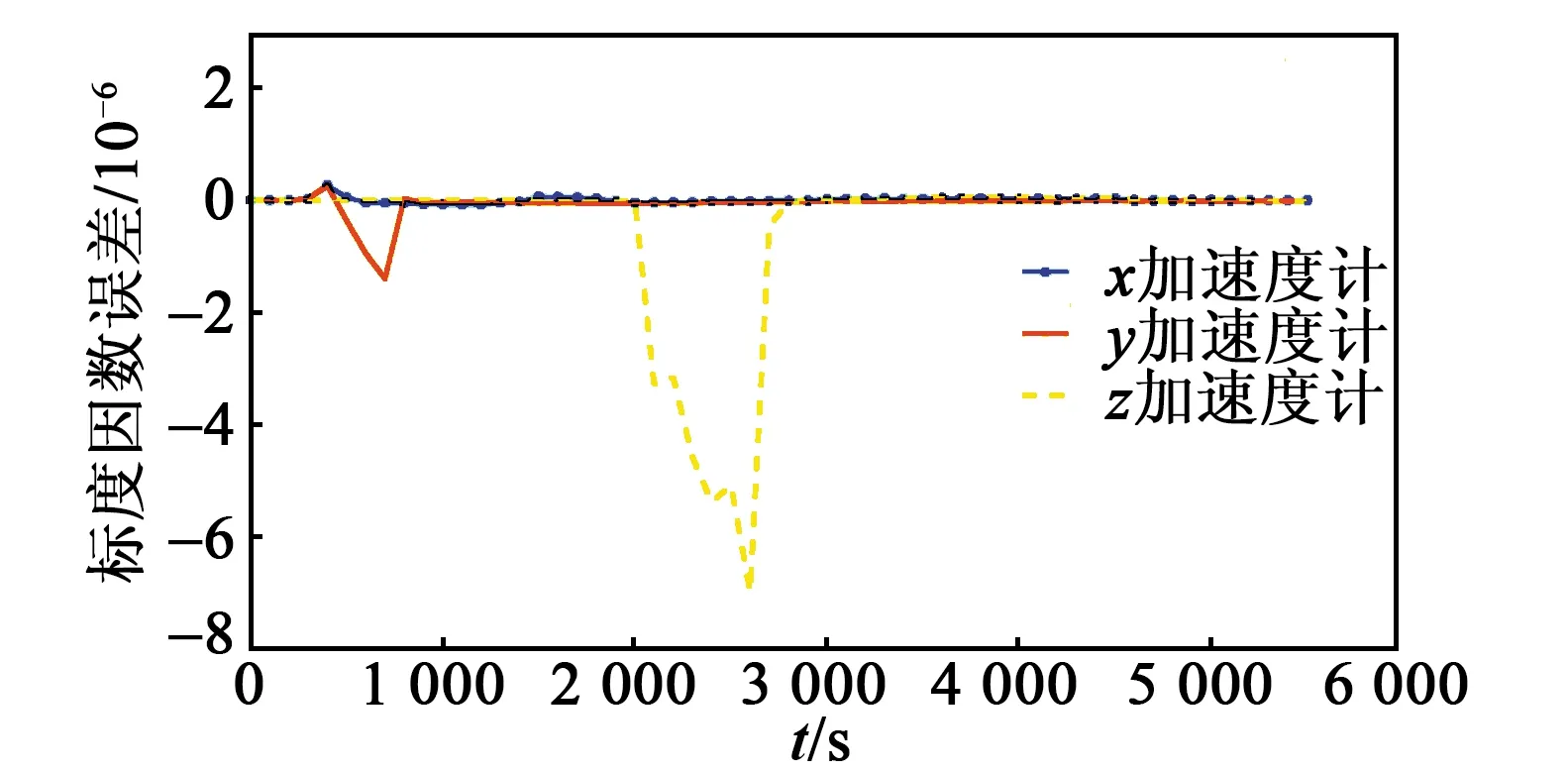
图6 加速度计标度因数误差

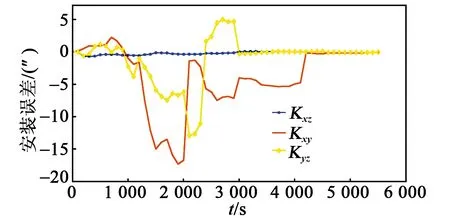
图7 加速度计安装误差

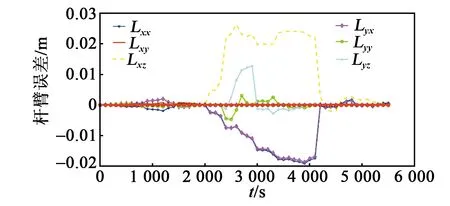
图8 杆臂误差

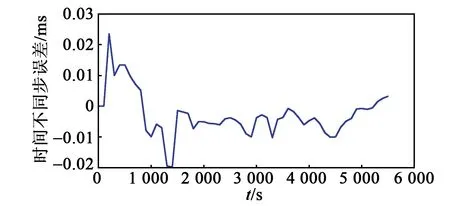
图9 时间不同步误差

5 试验验证

为了验证文中所述两级标定方法的可行性，将实验室的某型光纤平台系统安装在两轴转台上，并按照所设计的标定路径进行标定测试实验。

第一次标定采用一级标定Kalman滤波器，在光纤平台系统上电稳定状态标出杆臂误差及时间不同步误差。光纤平台杆臂误差及时间不同步误差的6次标定统计结果方差如表3所示。

表3 杆臂误差及时间不同步误差标定统计结果

由表3可知，杆臂误差估计精度优于2 mm，时间不同步误差估计精度优于0.02 ms。将估计出的结果烧写进系统中，实现杆臂误差及时间不同步误差的离线补偿。

第二次标定采用二级标定Kalman滤波器，在光纤平台启动过程中进行系统级标定。光纤平台6次标定统计结果方差如表4所示。

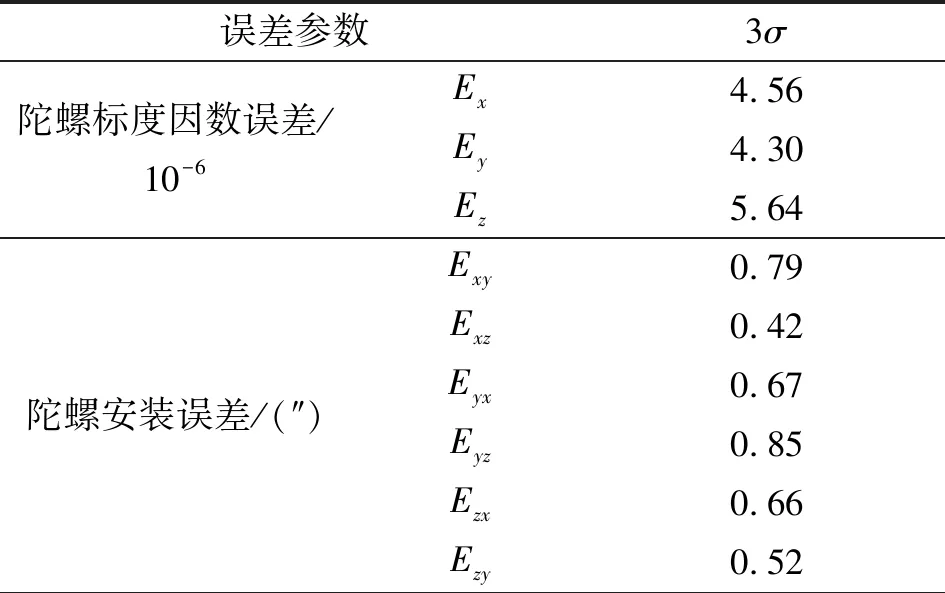
表4 光纤平台参数标定统计结果

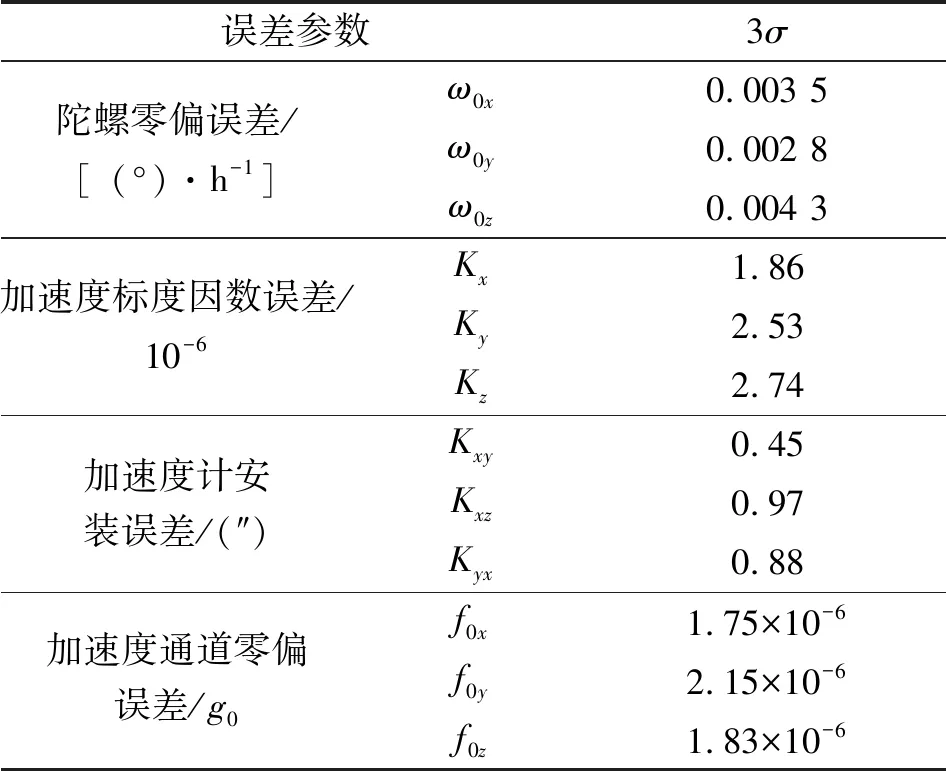
续表

由表4可看出，陀螺仪标度因数误差标定精度优于6×10-6、安装误差标定精度优于1″，零偏误差标定精度优于0.005 (°)/h，加速度标度因数误差标定精度优于3×10-6、安装误差标定精度优于1″、零偏误差标定精度优于3 μg。由表可知，误差标定精度满足高精度光纤平台的应用需求，且有效缩短了标定时间。

6 结束语

本文基于光纤平台系统误差参数的特点，提出了一种适用于高精度光纤平台系统的两级标定方法。通过采用分级标定的方式，既满足了系统的精度要求，又提高了光纤平台系统应用时的快速性。经仿真与试验验证，本文设计的标定路径与标定算法无需依赖转台即能精确估计出光纤平台的误差参数，且有效缩短了平台的标定时间，具有较高的工程应用价值。