基于双流降维EEMD-CNN滚动轴承故障诊断
2022-11-18郭梓良郝如江王一帆杨文哲赵瑞祥
郭梓良, 郝如江, 王一帆, 杨文哲, 赵瑞祥
(石家庄铁道大学机械工程学院,河北 石家庄 050043)
对工作中的轴承进行故障识别与诊断的过程中,常常受到噪声的干扰导致故障识别准确率降低。因此对噪声进行筛选和处理,是滚动轴承故障识别的关键所在[1]。
当今的轴承故障诊断主要是围绕着故障振动信号的特征提取和分类等方面进行研究。史东海等[2]通过使用传统方法对信号进行处理后使用PCA降维,随后采用K近邻算法对结果进行分类。姚峰林等[3]通过使用小波包变换对滚动轴承数据消噪处理后再进行极限学习机特征提取分类。汪朝海等[4]对原数据通过经验模态分解后使用卷积神经网络进行故障分类。上述方法对原始故障信号进行相应处理,削弱了噪声干扰信号所带来的影响,从而使得信号特征更易提取,但是仍存在着一定的不足。传统方法虽然能减少噪声带来的信号干扰,但是由于初始参数的影响,常常导致有用的特征信号被筛选清除。使用小波分解处理方法,因小波基参数需要多次实验分析确定,缺少信号处理的泛化性。EMD可以对信号进行自适应分解,但是会产生严重的端点效应并具有模态混叠的缺点。
为了解决上述问题,本文采用一种集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)、主成分分析算法(Principal Component Analysis,PCA)和一维卷积神经网络(one-Dimensional Convolutional Neural Network,1D-CNN)相结合的轴承故障识别的方法:首先将原始数据进行重构分解得到若干个本征模函数(Intrinsic Mode Function,IMF)分量,通过筛选能够充分表达出数据特征的一条IMF分量再进行PCA算法去冗余处理,其次将原始数据也经过PCA去冗余处理,并采用将PCA-IMF分量和经过处理的新数据作为一维卷积神经网络(1D-CNN)的输入数据,最后把处理后的数据投入到网络中进行多次迭代训练特征提取分类,为滚动轴承故障预防和故障研究提供了一种新方法。
1 信号分析常用方法
1.1 EEMD算法
EEMD方法是为了弥补EMD模态混叠现象而提出的,通过对EMD分解后的若干个IMF分量添加对应的高斯白噪声来改变分解过程中极值点的位置,从而可以有效地抑制模态混叠的产生。具体步骤如下:
(1)设定EEMD的运算次数z和高斯白噪声标准差n。
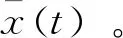
(4)重复步骤(1)和步骤(2)的操作z次后,筛选适当的IMF分量进行信号重构。
1.2 主成分分析(PCA)
当振动信号经过EEMD分解后仍存在干扰和冗余,这些干扰在网络训练时会影响网络准确性,因此需要筛选并去除其中的干扰值,提高IMF分量的表现力。
PCA算法通过计算样本向量中的特征值和均值,并通过投影运算便可以达到降维的目的。主要步骤如下:
(1)首先将数据进行中心化。
(2)计算样本的协方差矩阵ZZi。
(3)对协方差矩阵ZZi进行特征值分解。
(4)取最大的d个特征值所对应的特征向量ωi。
(5)将ωi投影成矩阵。
1.3 卷积神经网络(CNN)
随着机器学习的发展,卷积神经网络在数据处理及分类等方面取得了巨大的进步。卷积神经网络是通过类似神经元的反应及反馈,利用卷积运算提取训练样本中的特征,其主要包括卷积层、池化层和全连接层。由于CNN超强的学习和特征提取能力因此广泛用于工学的各个领域。
卷积层是通过卷积块对数据进行局部运算并产生特征图。池化层可以通过特征降维,提高网络活性。全连接层是将上层传入的数据进行进一步特征提取并将提取出的特征输入Softmax函数进行分类。
2 故障诊断步骤
为了防止EEMD分解所带来的特征缺失,提高模型的鲁棒性和泛化性,提出基于EEMD分解和原始数据相互结合的方法。具体滚动轴承故障识别实验方法如图1所示。
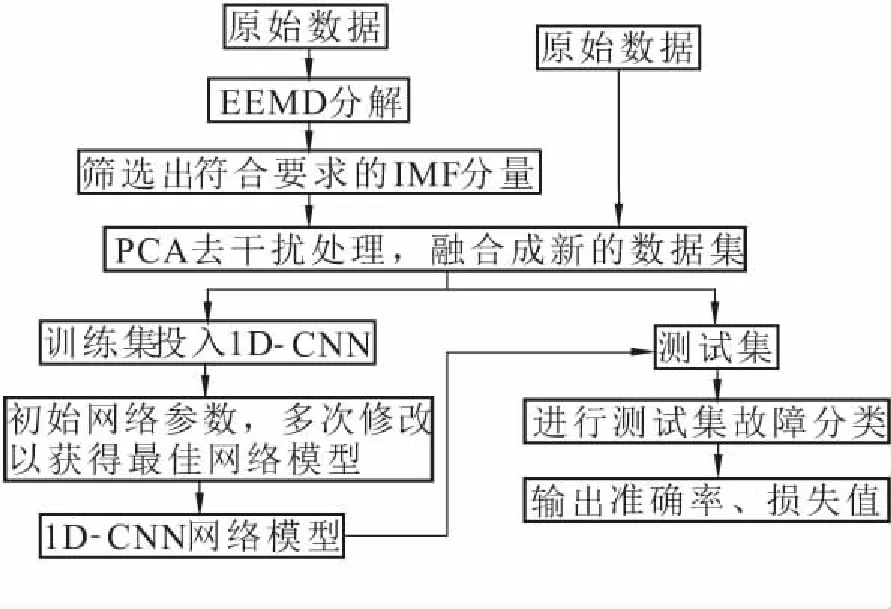
图1 EEMD-PCA-1D-CNN故障分类流程
3 实验验证
3.1 信号处理
本文数据是采用美国西储大学电机轴承故障状况实验,通过人为电火花破坏滚动轴承形成三种故障类型,对比正常类型,并筛选不同工况、载荷以及转速下的振动信号,具体数据选取如表1所示。

表1 轴承信号选取参数
根据本文上述的实验方法,首先对数据进行EEMD处理,通过筛选适合的IMF分量对分解后的信号进行重构。相关系数可以用来表现分解后的IMF分量与原数据的相关程度。通过计算振动信号的谱峭度值ku可以发现运行系统中的异常,当轴承在正常运行时,谱峭度ku约等于3;当轴承发生故障或者运行不正常时,此时的谱峭度将会偏离正常值[5]。
相关系数的计算公式:
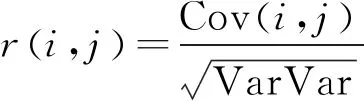
(1)
式中:i,j为两个变量;Cov()为i,j的协方差;Var[]为i,j的方差。求得各IMF分量的相关系数并取绝对值,绝对值越大则表明该IMF分量所体现的故障振动信号所包含的原始信号相关程度越高。
根据上述的方法,计算各个IMF分量的相关系数和谱峭度,部分结果如表2、表3所示。为了体现EEMD算法更能体现出故障信号特征,因此将原始数据经过EMD分解设置为对照组,并计算对照组的相关系数和谱峭度值,部分结果同见表2、表3。
由表2、表3可知,轴承故障越严重,数据经过EEMD分解后所得谱峭度与正常值偏差更大,故障特征信息更明显。由表2、表3可知,EEMD相比于EMD可以更有效的提取轴承信号的故障信息。通过计算分解后的各个IMF分量,将含有故障的轴承进行分解筛选,选取谱峭度与正常值3偏差较大、相关系数的绝对值较大的分量进行数据重构,并作为神经网络的输入数据集。

表2 EEMD-滚动体故障和EMD-滚动体故障(0.007 in)

表3 EEMD-滚动体故障和EMD-滚动体故障(0.014 in)
3.2 网络模型参数
将重构后的信号输入主成分分析算法中计算,按照7∶3的比例分为测试集与训练集,放入一维卷积神经网络中。本文基于经典卷积网络LeNet-5模型并多次调试,最终选取的各个参数如表4所示。

表4 卷积层参数
本次实验所使用的深度学习框架为Tensorflow,编程语言为Python。计算机配置为锐龙R7-5800H,英伟达GeForce RTX3050Ti,16G内存。此次实验每组数据中包括1 000个数据点,通过五折交叉验证法确定最优网络模型,测试阶段重复5次,最终测试结果取均值。
4 实验结果分析
通过多次对比实验,10类故障信号分类准确率和损失值如图2、图3所示,经过500次迭代后准确率趋于稳定。通过t-SNE技术对原始数据和经过训练的模型进行特征可视化分类,如图4所示(只模拟分类拟合情况,横、纵坐标无实际意义),未经过模型训练的各个故障混乱,经过训练后的模型故障标签7和标签8发生分类错误。通过图5可知EEMD算法过程中存在端点效应而导致分类错误。
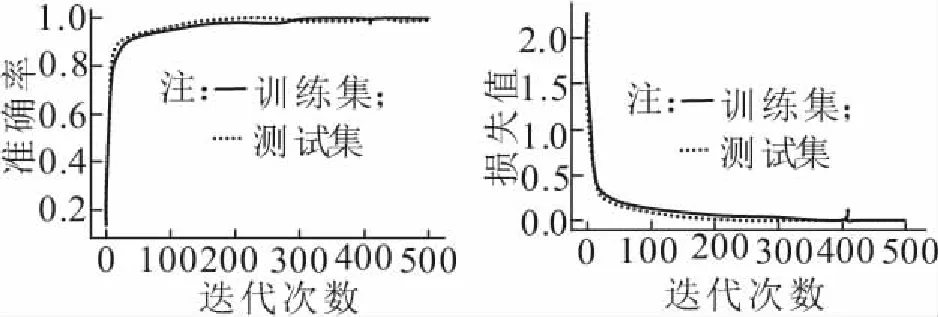
图2 准确率 图3 损失值

图4 特征可视化 图5 混淆矩阵
5 对比实验验证
为了验证本文所采用的轴承诊断方法的适用性和准确性,通过使用机器学习中的分类方法对处理后的数据进行对比。将上述处理好的数据作为输入数据输入到EEMD-CNN和随机森林中,10次实验测试结果为:本文方法平均准确率98.6%,EEMD-CNN平均准确率92.3%,EEMD-随机森林平均准确率86.6%。可知,通过使用EEMD-PCA-1DCNN的方法可以有效的提取故障类型的振动信号特征并分类,相比于其他算法有最高的平均准确率(98.6%),特征识别及分类效率有着明显的提高,证明本文所提方法的可行性与有效性。
6 结束语
因轴承故障的振动信号复杂且包含有多种干扰,本文提出一种基于EEMD-PCA-1D-CNN的故障诊断方法,由对比结果可知,本文的方法在轴承故障诊断分类中准确率更高。本文在EEMD处理时数据产生了端点效应而导致准确率降低,还应探究多种网络及算法优化以获得最优模型,并通过变工况设计实验增加网络模型的鲁棒性和泛化性。
