2021年日本东京大学入学考试理科数学试题解析
2022-11-18陈映彤广西师范大学数学与统计学院541004
彭 刚 陈映彤 (广西师范大学数学与统计学院 541004)
东京大学是日本最顶尖的综合性大学,汇聚了日本一流的人力资本和学术资源[1].在日本 近代数学的发展中,东京大学扮演了举足轻重的角色——1877年日本东京数学会和东京大学 理学部成立,日本现代数学研究正式拉开帷幕.曾获菲尔兹奖和沃尔夫奖的著名数学家小平邦彦(Kunihiko Kodaira,1915—1997)就曾在东京大学工作过.时至今日,东京大学仍是日本最重要的数学研究机构.
与日本其他著名高校一样,东京大学每年通过大学入学考试为其选拔大批优秀后备人才,不断增强本校数学研究的力量.日本著名大学入学考试作为选拔高水平人才的得力方式,其试题的设置方式与内容均值得我们借鉴.本文对东京大学2021年数学入学考试试题进行解析,希望对当前中国实施的“强基计划”提供参考.
1 试题概述
日本国公立大学的选拔一般由两场考试构成——学生首先需通过全国统一的大学入学考试,成绩合格后才有资格参加国家公立大学自主组织的入学考试.东京大学自主组织的入学考试数学试题分为理科卷和文科卷,本文介绍的即为2021年东京大学入学考试中的理科数学试题.
依据日本最大的教育辅导社河合塾提供的数据,2021年东京大学理科数学试题的总体难度与2020年持平,较2019年有所上升.试题中的题目均为解答题,共6大题(每个大题都包含若干个小题),总分为120分,考试总时长为150分钟.从内容方面来看,这些题目涉及的知识领域包括初等数论、初等代数、解析几何以及微积分.下面我们对这6道问题进行解析.
2 试题解析
第1题已知a,b为实数,平面直角坐标系中有抛物线C:y=x2+ax+b,它与抛物线y= -x2有两个交点,且两个交点的横坐标分别满足x1∈(-1,0),x2∈(0,1).
(1)在平面直角坐标系中表示出点(a,b)的范围;
(2)在平面直角坐标系中表示出抛物线C的范围.



图1
(2)设(1)中点(a,b)的范围为D,抛物线通过的范围设为E,(x,y)为E中任意一点,则(x,y)满足的条件为:在xOy平面上,满足y=x2+ax+b且(a,b)在D中;这等价于:在aOb平面上,直线b=-xa+y-x2与D有公共点.
令g(a)=-xa+y-x2,可分为以下四种情况讨论:
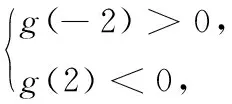


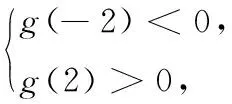
综上可知,E的边界为y=x2-2x,y=x2+2x,y=x2-2,进一步可得到直角坐标系中E的图形,如图2.

图2
点评本题主要考查平面内两条抛物线的位置关系,内容属于“解析几何”,难度层次为“标准”①(1)①河合塾将试题难度分为“易”“较易”“标准”“较难”和“难”五个等级,日本高校理科类数学试题大多集中在“较易”“标准”和“较难”这三个等级..本题分为两小问,第(1)问较为常规,本质上是关于一元二次方程根的分布问题,解决策略是将其转换为一元二次函数的图象与x轴的交点情况来处理.第(2)问要求动抛物线的移动范围,此类问题在我国高考和竞赛中都较为少见,其解决策略是“反客为主”,把(a,b)视为动点,从而将动抛物线与定抛物线的相交问题转化为动直线与定区域的相交问题,具有一定的挑战性.
第2题已知f(z)=az2+bz+c(a,b,c为复数),i为虚数单位.
(1)设α,β,γ为复数,且f(0)=α,f(1)=β,f(i)=γ时,请用含α,β,γ的式子表示a,b,c;
(2)当f(0),f(1),f(i)均为区间[1,2]中的实数时,请在复平面内表示f(2)的范围.

(2)设f(2)=4a+2b+c=ω,将(1)的结果代入f(2)中,有
=α(-1-2i)+β(3+i)+γ(-1+i),
其中,α,β,γ是满足1≤α≤2,1≤β≤2, 1≤γ≤2的实数.
设-1-2i=z1,3+i=z2,-1+i=z3,则当1≤α≤2且1≤β≤2时,由复数加法的几何意义可知,αz1+βz2的范围为一个平行四边形(图3).

图3 图4
假设这个平行四边形的边界及内部为D,D中的各点再加上γz3(1≤γ≤2),便可得到ω即f(2)的范围(图4).
点评本题主要考查复数的运算及其几何表示,内容属于“初等代数”,难度层次为“较难”.本题有两问,第(1)问求a,b,c的表达式,为常规计算.第(2)问求f(2)的范围,涉及三个变量,难度较大;此问的解题策略是“逐步推进”——先研究两个变量的情况,然后在此基础上研究三个变量.就表达方式而言,求解第(2)问时既可以利用复数加法的几何意义,也可以转换成向量的加法,二者本质上是相通的.
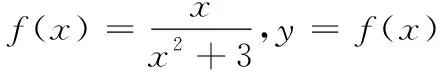
(1)若C与l只存在一个与点A不同的交点,求该点的横坐标;
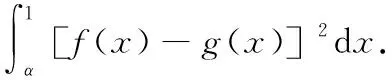


下面使用换元法来计算I2和I3.


点评本题主要考查切线方程求解及定积分的计算,属于“微积分”的内容,难度层次为“标准”.本题中的求导运算和积分运算均比较常规,但对计算的准确性提出了较高的要求.
第4题回答以下问题:
(1)若正奇数K,L和正整数A,B满足KA=LB,且K与L除以4的余数相同,证明:A与B除以4的余数也相同;
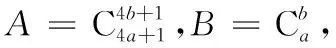


解(1)由于4|(K-L),令K-L=4n(n为整数),则K=L+4n.又KA=LB,故(L+4n)A=LB,即L(A-B)=-4nA,而L为奇数,所以A-B是4的倍数,从而得到A与B被4除的余数相同.
(2)依题可知,
令r0=4a(4a-4)·…·(4a-4b+4),
r1=(4a+1)(4a-3)·…·(4a-4b+1),
r2=(4a-2)(4a-6)·…·(4a-4b+2),
r3=(4a-1)(4a-5)·…·(4a-4b+3),
以及t0=4b(4b-4)·…·8·4,
t1=(4b+1)(4b-3)·…·5·1,
t2=(4b-2)(4b-6)·…·6·2,
t3=(4b-1)(4b-5)·…·7·3,
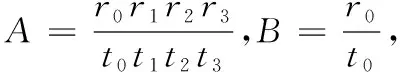

(3)易知r1≡t1(mod 4),r3≡t3(mod 4),又2|(a-b),故4|(2a-2b),即2a≡ 2b(mod 4),从而有(2a-1)(2a-3)·…·(2a-2b+1)≡(2b-1)(2b-3)·…·(2b-2b+1)=(2b-1)(2b-3)·…·3·1(mod 4).

点评本题主要考查整除和同余理论,内容属于“初等数论”,难度层次为“较难”.本题共有4个小问,并且它们环环相扣,问题的设计很精妙.本题引入了组合数,因而增加了题目的难度,解题者需要根据(1)中的结论,将组合数展开中的诸多整数按照模4的余数进行分类,并通过换元来简化运算,具有很强的技巧性.
第5题已知α为正实数,关于θ的函数f(θ)为平面上A,P两点距离的平方,这两点的坐标分别为A(-α,-3),P(θ+sinθ,cosθ)(0≤θ≤π).
(1)证明:当0<θ<π时,存在唯一的θ使得f′(θ)=0;

解(1)依题可知f(θ)=AP2=(θ+sinθ+α)2+(cosθ+3)2,则
f′(θ)=-4sinθ+2(θ+α)cosθ+2(θ+α),
f″(θ)=-2(θ+α)sinθ-2cosθ+2,
f‴(θ)=-2(θ+α)cosθ.
由f‴(θ)的正负可得到f″(θ)的单调性,如下表所示:
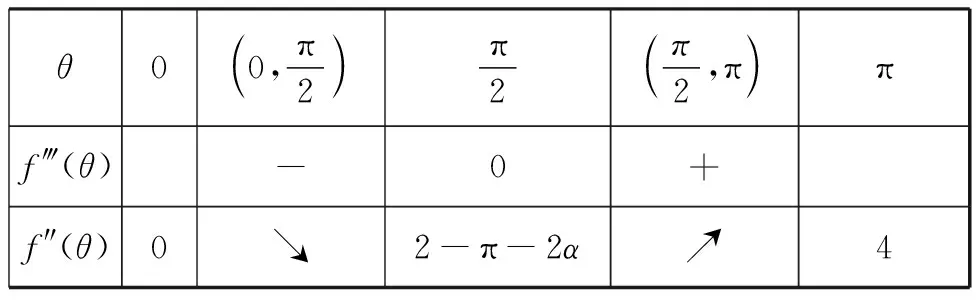
θ00,π2 π2π2,π πf‴(θ)-0+f″(θ)0↘2-π-2α↗4

由f″(θ)的正负继续可以得到f′(θ)的单调性,如下表所示:

θ0(0,β)β(β,π)πf″(θ)-0+f'(θ)4α↘f'(β)↗0
因为f′(θ)在(β,π)内单调递增,所以f′(β)
(2)由f′(θ)的正负可以得到f(θ)的单调性,如下表所示:

θ0(0,γ)γ(γ,π)πf'(θ)+0-0f(θ)f(0)↗f(γ)↘f(π)

点评本题主要考查零点定理、函数的导数与函数的单调性之间的关系,属于“微积分”的内容,难度层次为“标准”.本题有两小题,其中第(1)题十分有特色,解答过程中涉及多个存在性问题.与第3题主要考查计算不同,本题带有浓厚的“分析”味道,解题者既需要清晰的逻辑思维,又需要有较强的直觉能力.
第6题已知b,c,p,q,r为常数,下式为关于x的一个恒等式:
x4+bx+c=(x2+px+q)(x2-px+r).
(1)当p≠0时,用p,b表示q,r;
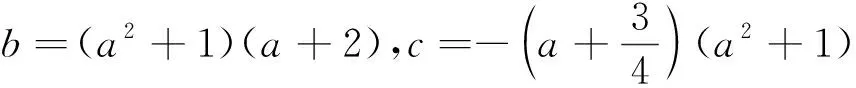




故满足条件的一组整式f(t)与g(t)为f(t)=t2+1,g(t)=(t2+1)(t+2)2.



②当p≠0时,由(2)知p满足
[p2-(a2+1)][p4+(a2+1)p2+(a2+1)(a+2)2]=0,



点评本题主要考查代数式的运算,内容属于“初等代数”,难度层次为“较难”.本题具有较强的综合性,解题步骤也较多,对解题者的计算准确性要求很高.此外,本题涉及较多的字母(除了主元x外,还有6个表示常量的字母a,b,c,p,q,r),因而解题者需要具备较强的信息处理能力.
3 结语
2020年1月,中国教育部颁布文件《关于在部分高校开展基础学科招生改革试点工作的意见》[2].该文件聚焦国家重大战略需求,决定从2020年起取消高校自主招生考试,在试点的36所高校实施“强基计划”,以提升基础学科人才选拔和人才培养质量.
通过对中国2020年“强基计划”中部分大学的试题与东京大学的入学试题的对比,不难发现两国的试题各具特点.中国实施“强基计划”的部分著名高校试题题目数量较多,比如北京大学和清华大学的试题都是20道,复旦大学的试题有33道,并且题型均为选择题[3]-[5],因而考查的知识面比较广;而东京大学的自主招生考试题目较少,但均为解答题,因而能更深入地考查学生的数学思维和数学表达能力.此外,东京大学入学试题对微积分这一内容的要求很高;事实上,微积分这一内容是日本各大高校入学考试中的重要考查对象,相对而言我国的高校在这方面则要求不高.东京大学等日本顶级大学的入学数学试题为当前中国数学资优生的培养与选拔提供了重要参考.
