动车组轴箱轴承在线监测可靠性评估模型研究*
2022-11-18高明亮孙洪亮刘德权石海明
高明亮 赵 明 高 珊 孙洪亮 于 闯 刘德权 石海明
(中车长春轨道客车股份有限公司国家轨道客车工程研究中心, 130062, 长春∥第一作者, 高级工程师)
动车组轴箱轴承运行环境复杂,其机理特征很难评价,运营服务商对此类系统提出了高可靠性要求来避免灾难性意外故障的发生。过去几年来,人们对动车组轴箱轴承的PHM(故障预测与健康管理)研究给予了极大的关注,PHM为状态监控、健康评估和转向架的最佳控制提供了全面的解决方案[1]。通过实施PHM技术,动车组轴箱轴承可避免即将发生的故障,因此可显著提高其可用性和可靠性。文献[2-3]表明,PHM的重要部分集中在可靠性评估上,尤其是剩余使用寿命预测。由于测试仪器技术的进步,相关系统的运行状态和环境的信息采集能力已大大增强。因此,开发了一种简便的可靠性评估模型——PH(比例风险)模型[4]来监控系统性能以及评估系统的健康状态。该模型采用信息伴随的寿命效应对可靠性进行评估,是非常有前景的轴承可靠性预测方法。该模型已在各种关键工程系统的可靠性分析领域中被广泛使用,例如飞机发动机、牵引车的传动、铁路货车轴承[5-7]等领域。
退化过程作为协变量在PH模型中起着至关重要的作用。通常将退化过程建模为随机过程,例如:维纳过程[8],伽玛过程[2],连续时间马尔可夫链[9]。其中,维纳过程在处理时间上具有异常出色的能力,目前已被广泛应用于退化过程的建模中。
此外,评估方法旨在进行在线可靠性评估,特别是对于转向架轴承,实时计算能够有效提供健康状况评估支持和系统优化。综上,本文提出了一种以寿命因素和维纳退化作为协变量的转向架轴箱轴承在线状态监测的可靠性评估方法。
该评估方法重点体现在:
1) 将具有时移的非线性维纳退化过程作为协变量集成到PH模型中。
2) 采用提出的近似技术,可以从整个生命周期的角度得出所有相关的可靠性量转移概率矩阵。
1 动车组轴箱轴承在线监测可靠性评估方法
1.1 联合退化过程的技术研究
定义一个在线状态监控系统,采用PH模型评估其可靠性特征。其危害率函数取决于系统寿命和监视信息。
危险函数h(·)可以表示为:
h(t,X(t))=h0(t)ψ(X(t);γ)
(1)
式中:
h0(t)——基准风险方程;
t——监视时间;
γ——回归系数向量;
ψ(·)——生存函数;
X(t)——协变量过程。
根据定义,在给定监视状态X(t)的情况下,监视时间t(t∈R+)的条件危害率函数可以定义为:
t+Δt|Tf>t,X(t))/Δt
(2)
式中:
Tf——失效时间;
P(·)——累计生存概率函数。
式(2)中,{X(t),t∈R+}表示系统的退化过程。
由式(2) 可以推导出条件可靠度函数R(·):
R(t|X(u),0≤u≤t)=
P(Tf>t|X(u),0≤u≤t)=

(3)
式中:
u——漂移参数。
从应用角度出发,维纳过程适合于退化建模,因为系统的退化程度可以看作是大量正态分布增量的总和。
因此,将退化过程X(t)建模为:
X(t)=X0+σW(A(t))+uA(t)
(4)
A(t)=t-t0
(5)
式中:
t0——初始监视时间;
X0——初始退化量;
W(·)——标准布朗过程;
σ——标准偏差。
考虑到X(t)的时变和随机特征,计算式(3)的期望时难以通过积分实现可靠性的评估。因此,为了解决该问题,应引入一些变量的近似值。
1.2 状态和时间的近似计算
针对状态空间和时间提出了一种近似技术。
首先,将状态空间的长度以等间距d分割,将连续的退化路径划分为M个离散状态,在临界水平Y存在的情况下,合理选择其为d=2Y/(2M-3)。通过这种近似,可以将连续退化过程表示为马尔可夫链。其状态空间Ω由M个离散状态组成,其中S0,S1,…,SM-2表示退化状态下的生存概率,SM-1表示吸收状态下的生存概率。
图1显示了系统退化过程随时间变化的曲线。从图1可以看出,X(t)的范围为[id-d/2,id+d/2],i∈Ω。
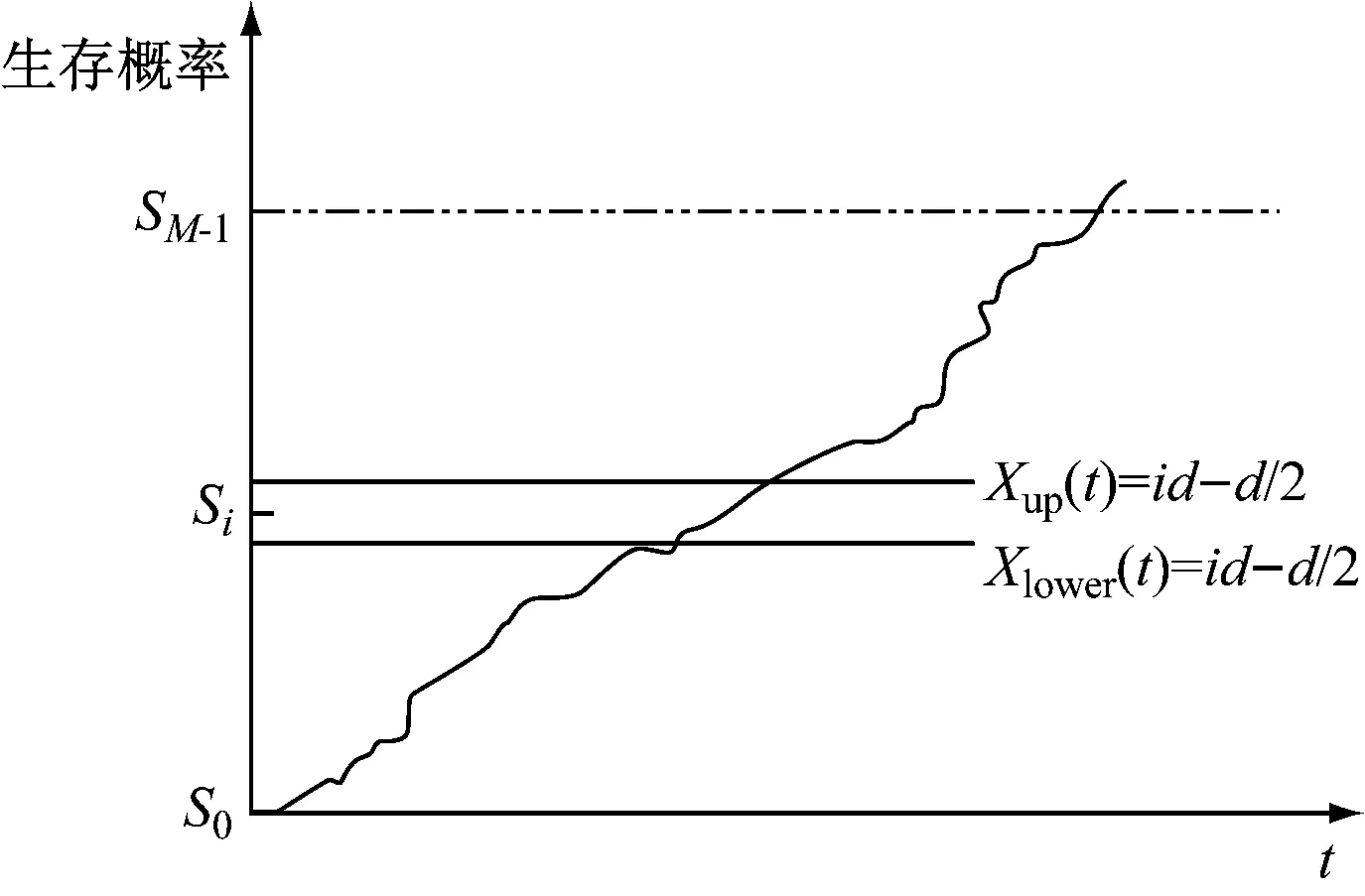
图1 退化过程的离散化曲线Fig.1 Discretization curve of degraded process
结合Tf定义联合退化过程V(t)=(Tf>t,X(t))>t。则对于所有0≤t1 P(Tf>t,X(t)=j|Tf>s,X(s)=i,X(t2)=i2, X(t1)=i1)=P(Tf>t,X(t)=j|Tf>s, X(s)=i)=Λi,j(s,t) (6) 其中,Λi,j(s,t)是联合分解过程V(t)的转移概率。该过程体现了退化系统的特征,并且随机行为可由转移概率矩阵Λij(s,t)描述。 对于等间距为δ(δ>0)的区间,采用δ来离散时间轴。 当退化系统运行时间的长度大于选定的寿命期限时,认为该系统(尤其是关键系统)不适合继续操作。 假设当退化系统的执行时间大于整个生命周期T时,退化系统的RUL(剩余使用寿命)为零,其中T=Nδ,N为间隔数。 因此,考虑离散时间tw=wδ。其中,w表示从开始到当前时刻tw的步数,w=0,1,…。 对于该时间的离散化,可以将V(t)转移到其离散时间对应项V(wδ),由此转换概率可以写为: Λij(w1δ,w2δ)=P(Tf>w2δ,X(w2δ)= j|Tf>w1δ,X(w1δ)=i) (7) 式(7)中,0≤w1 因此,退化过程从状态i到状态j的单步转移概率可以表示为: P(X((w+1)δ)=j|Tf>(w+1)δ,X(wδ)=i)= P(lb<ΔX(wδ)≤ub)= (8) lb和ub定义如下: 1) 当i,j∈[0,M-2]时,lb=max(0,(j-i)d-d/2),ub=(j-i)d+d/2; 2) 当i∈[0,M-2]时,M=M-1,则lb=(M-i)d-d/2,ub=+∞。 因M-1是吸收状态,故P(X((w+1)δ)=M-1|Tf>(w+1)δ,X(wδ)=M-1)=1。退化系统不是自恢复的,并且对σ和u的适当选择将导致自恢复的概率可以忽略。 与系统的整个生命周期相比,δ是足够小的值。因此,在给定当前状态X(wδ)=i的情况下,该系统在下一个长度为δ的时间间隔中存活的概率可以近似为: P(Tf>(w+1)δ|Tf>wδ,X(wδ)=i)= (9) 式(9)中,w∈[0,N-2],Xi表示退化水平的对应状态Si。 另外,假设系统的整个生命周期为Nδ,这意味着在P(Tf>Nδ|Tf>(N-1)δ,X((N-1)δ)=i)=0之后继续运行是不合适的。基于式(5)和式(6),联合失效时间过程V(wδ)的单步转移概率矩阵的元素可以写成: Λi,j(wδ)=P(Tf>(w+1)δ,X(w+1)δ=j|Tf>wδ, Xwδ=i)=P(X((w+1)δ)=j|Tf> (w+1)δ,X(wδ)=i)·P(Tf>(w+1)δ| Tf>wδ,X(wδ)=i) (10) 结合单步转移概率矩阵Λ(wδ),可以将联合退化过程的整个生命周期跃迁概率矩阵组织为式(11)。其中,UM是M个元素的单位向量,N是步骤数。 (11) 式(11)的最后一列表示故障状态的转移概率。 由式(11)可见,矩阵的结构实质上可加速矩阵的运算,例如乘法和求逆等运算。 式(11)中P的最后一列给出了该退化过程直接从状态i∈{0,1,…,M-1}过渡到故障状态的可能性。因此,P可划分为: (12) 其中,B是MN×MN矩阵;0是MN个元素的零向量;PF=(I-B)UMN,I是单位矩阵,UMN是MN个元素的单位向量。 (13) 基于划分的整个生命周期转移概率矩阵P,可以得出RUL的概率。 本文提出了一种用于动车组轴箱轴承的在线监测可靠性评估方法。 该方法采用具有时移的非线性维纳过程来表示退化,然后将其作为协变量并入PH模型来描述转向架轴箱轴承故障时间的分布。利用所提出的近似技术,使用转移概率矩阵导出了相关可靠性量的封闭形式公式。与传统方法相比,这些可靠性量的计算可以通过较少的计算工作来完成,并且能够获得实时可靠性评估。
1.3 退化系统可靠性量的推导

2 结语
