凹坑翅片换热器在单轨列车空调机组的应用
2022-11-17魏秀琴路晓鹏
魏秀琴,金 星,路晓鹏
(柳州铁道职业技术学院,广西 柳州 545416)
0 引言
随着城市轨道交通的快速发展,单轨交通与地铁相比较,具有振动噪声小、投资省、对环境影响小、曲线半径小、爬坡能力强等优势,多在国内重庆、芜湖等城市应用。单轨列车空调系统是保证乘客乘坐舒适性的一个重要系统,能够使车厢内保持合适的温度和湿度,为乘客营造良好、舒适的环境。近年来,城轨列车空调机组消耗功率占列车牵引动力能耗的40%左右[1],降低空调机组能耗对列车空调系统有着重要的现实意义[2]。列车空调机组通常设置在车顶上,空调机组的体积和质量会受到一定的限制,因此,如何实现空调机组小型化、轻量化也是需要考虑的现实问题。蒸发器和冷凝器是空调机系统的换热装置,其换热性能的好坏将影响到制冷剂与外部热源的换热效率,在提高空调能效方面起着非常重要的作用[3]。改进空调换热器的结构和提高其换热效率,对空调系统轻量化和节能有着重大意义。
目前单轨车辆空调的冷凝器和蒸发器基本上都采用管翅式换热器。研究表明,对于管翅式换热器,空气侧的热阻约占整个换热器热阻的80%左右,因此减小空气侧热阻,提高空气侧的换热系数对于改善换热器整体性能非常重要[4]。为了使换热器空气侧的换热性能强化,可以通过改变翅片表面的几何形状来实现。主要形状有百叶窗型翅片、纵向涡翅片、波纹型翅片[5-7]等。近年来,学者们研究提出了一种新型凹坑或球突翅片,在保证不破坏翅片完整性的条件下,在平直翅片表面上冲压形成凹坑或球突,这些凹坑或球突能使流体流过时对流体产生扰动,产生涡流,使流体的掺混程度增强,达到强化换热的作用。目前,对于凹坑翅片在列车空调换热器上的应用研究非常少,所以本文基于半球状凹坑翅片应用在列车空调机组换热器上的实际,研究了在翅片表面冲压凹坑后,分析不同工况下,圆管与凹坑翅片空气侧的流动及换热影响,为空调换热器设计及实际应用提供参考。
1 凹坑翅片结构模型
1.1 凹坑翅片描述
图1为本文物理研究模型。翅片管为四排管,翅片管材料为铜,采用错排方式布置;翅片为矩形翅片,材料为铝;在其表面冲压有凹坑,在每个圆管周围按照一定规律冲压有六个半球状的凹坑。
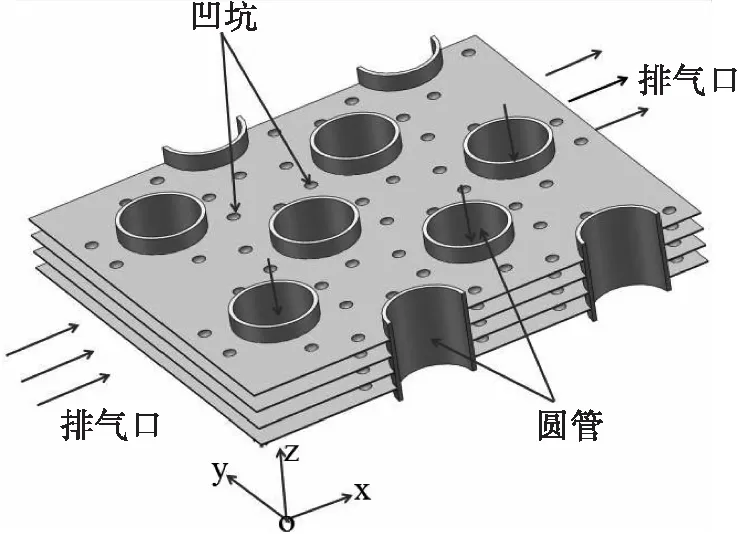
图1 圆管凹坑翅片模型示意图
1.2 凹坑翅片结构参数
如下页图2所示,图2给出了换热器圆管和凹坑的布置位置。凹坑的主要几何参数为:翅片长度L1、翅片厚度δf、管间距(横向S1、纵向S2),圆管外径D、圆管厚度δt、翅片厚度δf、翅片间距Tp、凹坑半径rd、凹坑中心距圆管中心间距Ld、凹坑圆心夹角α。基本结构参数如表1所示。

表1 基本结构参数表(mm)
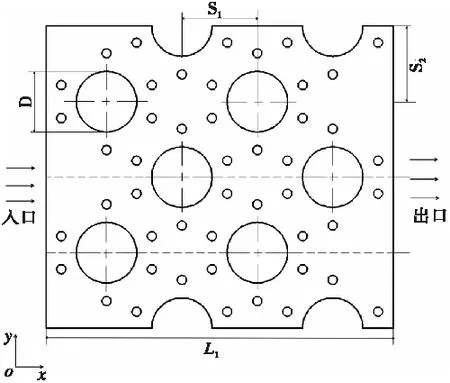
(a)带凹坑翅片圆管换热器翅片单元
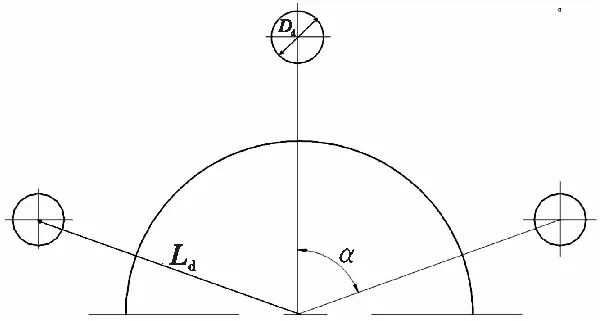
(b)凹坑的参数和位置
2 数学模型及边界条件
2.1 控制方程
计算所采用的计算方程如下[8]:
连续性方程:
∂(ρui)/∂xi
(1)
动量守恒方程:
∂(ρuiuj)/∂xi=-∂ρ/∂xi+∂(η∂ui/∂xi)/∂xi
(2)
能量守恒方程:
∂(ρcpuiT)/∂xi=∂(λ∂T/∂xi)/∂xi
(3)
式中:ui——三个方向速度;
p——流体压力;
T——流体温度;
cp——流体定压比热容;
λ——流体的导热系数;
ρ——流体密度;
η——流体的动力黏性系数。
2.2 计算模型
由于整个换热器中圆管和翅片数量较多,如果要对完整的换热器模型进行计算是非常困难的,因此对模型进行简化,选取上下两层翅片和圆管外壁所形成的通道作为数值计算的区域,如图3所示。为保证在实际应用中入口流体温度和速度均匀,将计算区域入口上游延长1倍圆管管径;为保证出口无回流影响,出口向下游延长5倍圆管管径。
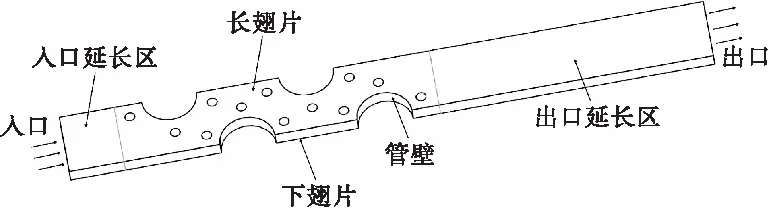
图3 计算区域示意图
2.3 计算边界条件设定
在本计算中,为了简化计算,假设圆管管壁为等温边界条件,设定管壁的温度Tw=40 ℃,速度为无滑移边界条件。本计算中,由于翅片的厚度只有0.2 mm,翅片和管外壁的接触热阻以及翅片本身的导热温差均被忽略,设定翅片温度恒定为40 ℃,圆管管壁温度恒定为常数设置为40 ℃。入口边界给定均匀速度和均匀温度,空气进口速度uin为1.5~4 m/s,空气进口平均温度Tin为30 ℃,出口边界设为自由压力出口。上下面边界采用对称性边界条件,左右面边界采用对称性边界条件。
2.4 网格无关性验证
在进行数值计算时,若网格数目较少,计算收敛性得不到保障,但是计算数目太多,增加计算机的负荷。因此,在划分网格时,不但要考虑求解的精度,还要考虑计算机配置的限制,缩短数值计算的时间。为了保证计算结果的准确性和网格的独立性,对网格独立性考核。网格划分如图4所示。

图4 网格划分示意图
当在Re=893、R=1 mm、α=70°、TP=2.4 mm条件下,对3种不同网格下的计算结果进行无关性验证的数据处理,结果如表2所示。

表2 网格独立性考核结果表
从表2可以得出,增加网格数,平均努塞尔数变化逐渐减小,网格数为1 120 082时对应的平均努塞尔数与网格数为1 280 082时对应的均努塞尔数相比相差0.02%,阻力系数相差0.07%。当网格数为1 120 082以后,继续增加网格的数目,平均努塞尔数和阻力系数变化非常小,因此,可认为数值模型在网格数为1 120 082时计算结果具有独立性。
3 计算结果与分析
3.1 凹坑翅片的换热特性分析
图5是在rd=0.9 mm、α=70°、TP=2.45 mm时,两种翅片模型平均努塞尔数Num和阻力系数f随雷诺数Re的变化曲线。图5(a)表明,当Re从893逐渐增加到2 382时,两种翅片平均努塞尔数Num变化趋势相同,平均努塞尔数Num都随着Re的增加而增大,并且平均努塞尔数的增长速率随着Re的增加逐步平缓。这是由于随着空气的流速增加,使空气流动边界层厚度变薄,提升了换热能力,但是这种靠增大流体速度提升换热的能力是有限的。在雷诺数Re相同的条件下,凹坑翅片的Num明显高于平直翅片的,在Re=893~2 382范围内,凹坑翅片的平均努塞尔数Num与平直翅片相比,提升了21.8%~38.7%,凹坑翅片的换热能力相比平直翅片得到了明显提升。这是由于凹坑增强了对空气的扰动作用,流体边界层厚度被减薄,极大地提高了换热器的换热能力。由图5(b)分析发现,两种翅片的阻力系数f随雷诺数Re的变化趋势基本相同,都是先快速下降后逐渐平缓下降,与平直翅片相比,凹坑翅片的阻力系数提升了20.9%~37%。阻力系数反映了管翅式换热器翅片的阻力特性,阻力系数越大,耗功越多。产生阻力损失的原因主要有:空气在流动过程中,由于自身黏度会造成摩擦阻力损失,冲刷翅片和换热管表面而产生压差阻力,以及翅片上的凹坑对流体产生扰动,形成纵向和横向涡流造成阻力损失。
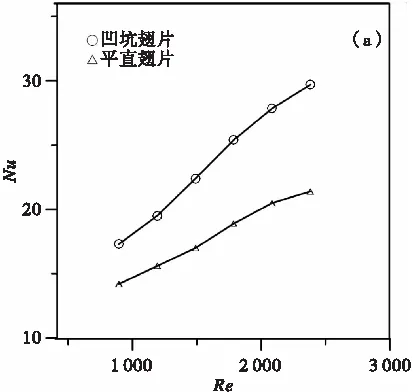
(a)Num
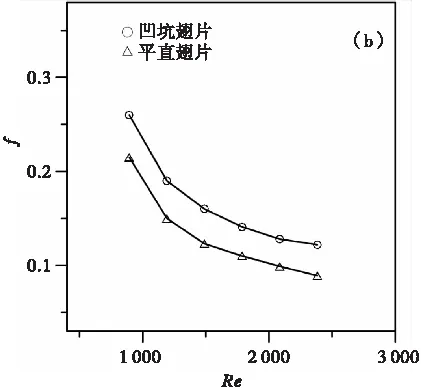
(b)f
3.2 凹坑翅片的综合性能评价
评价换热器的综合换热性能通常采用综合性能因子JF[9-10],JF综合考虑了流体传热和流动阻力两个方面的性能,其表达式如式(4)所示,其中Nu0和f0为平直翅片的平均努塞尔数和阻力系数。
同功耗强化传热评价因子:
JF=(Num/Nu0)/(f/f0)1/3
(4)
图6所示为JF随雷诺数Re的变化曲线,在Re为893~2 832范围内,凹坑翅片的JF的变化范围为1.14~1.24,JF1的数值均>1,说明相对于平直翅片来说,凹坑翅片可以使换热器获得更好的换热效果。
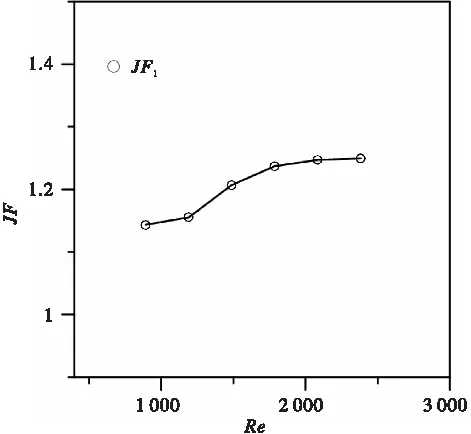
图6 JF1随Re的变化曲线图
4 结语
本文将凹坑翅片应用于单轨列车空调机组的换热器上,分析了不同工况下,圆管与凹坑翅片空气侧的流动和传热性能,并且对其综合性能进行评价,主要结论如下:
(1)在雷诺数Re为893~2 832时,采用凹坑翅片换热性能比平直翅片提升了21.8%~38.7%,阻力系数提升了20.9%~37%。
(2)在雷诺数Re为893~2 832时,综合性能因子的值均>1,与平直翅片相比,换热器采用凹坑翅片能有效地强化换热。
