基于BP神经网络的车桥耦合加速度预测及行车舒适度评价分析

张源翀，王龙林

(1.广西北部湾投资集团有限公司，广西 南宁 530022；2.广西交科集团有限公司，广西 南宁 530007)

0 引言

车桥耦合振动是指车辆和桥梁间的相互作用，即车辆驶过桥梁时引起桥梁振动，反过来桥梁振动亦造成车辆振动[1-2]。随着我国大跨桥梁的不断建设，其跨度、墩高、车速以及车流量等显著增大，因此车辆荷载和桥梁的振动问题更加突出[3-5]。通过细致全面地研究车桥耦合振动特性，将能极大提高桥梁的安全以及使用性能。

关于车桥耦合振动的特性，研究者们进行了一些有益的探索。施颖等[6]针对公路复杂桥梁建立了车桥耦合振动方程，并基于ANSYS软件进行了车桥耦合数值分析；李小珍等[7]以京沪高速铁路的斜拉桥为研究对象，研究了车速对桥梁挠度和行车舒适度的影响；杨建荣等[8]基于模态分析法推导了车桥耦合动力平衡方程，并以简支桥为例验证该理论方法的正确性；韩万水等[9]编制修正方法结合BDANS静力分析模块开展钢桁架连续梁桥车桥耦合振动分析，结果表明该方法同ANSYS分析结果以及实测数据较为吻合；肖新标等[10]运用数值仿真手段，引入欧拉贝努利梁假设对某简支梁进行了车桥耦合振动分析，通过和理论解对比验证了数值解的正确性；贺煊博等[11]采用接触约束法求解了某中承式拱桥车桥耦合振动响应，并研究了车辆过桥时桥梁吊杆的动力特性；刘勇等[12]基于LS-DYNA显示动力分析程序，研究重型车辆对大跨悬索桥的振动响应规律；陈水生[13]和赵露薇[14]分别研究了随机车流作用下公路斜拉桥和大跨拱桥的车桥耦合振动特性。上述研究可以看出，众多学者在车桥耦合领域取得了较为广泛的研究成果，并且其研究主要集中在数值模拟以及理论研究两个方面。然而，由于数值模拟和理论研究方法较难且实现过程较为复杂，许多从业者往往无所适从。近年来，神经网络方法由于结构简单、训练速度快，并且具有较高的动态仿真能力以及全局最优逼近等特点，可广泛应用于工程结构的响应预测分析中[15-17]。若能通过神经网络模型建立桥梁车桥耦合的响应预测模型，从而近似替代繁杂的数值和理论分析，将具有重要的科研意义和工程实用价值。

鉴于此，本文基于BP神经网络建立了车桥耦合加速度预测模型，以某典型工程的连续刚构桥为例进行加速度预测，并根据预测结果对该桥进行行车舒适度评价，以期为车桥耦合的加速度预测提供参考。

1 BP神经网络模型

BP神经网络由Rumelhant 和 Mcclelland提出，是目前应用最为广泛的多层前馈神经网络模型，主要包括输入层、隐含层和输出层[18-19]，其结构图如图1所示。BP神经网络计算过程由正向传播和误差反向传播两部分组成，各层神经元通过权值系数反映输入层和输出层的映射关系，从而达到强烈的非线性映射能力。

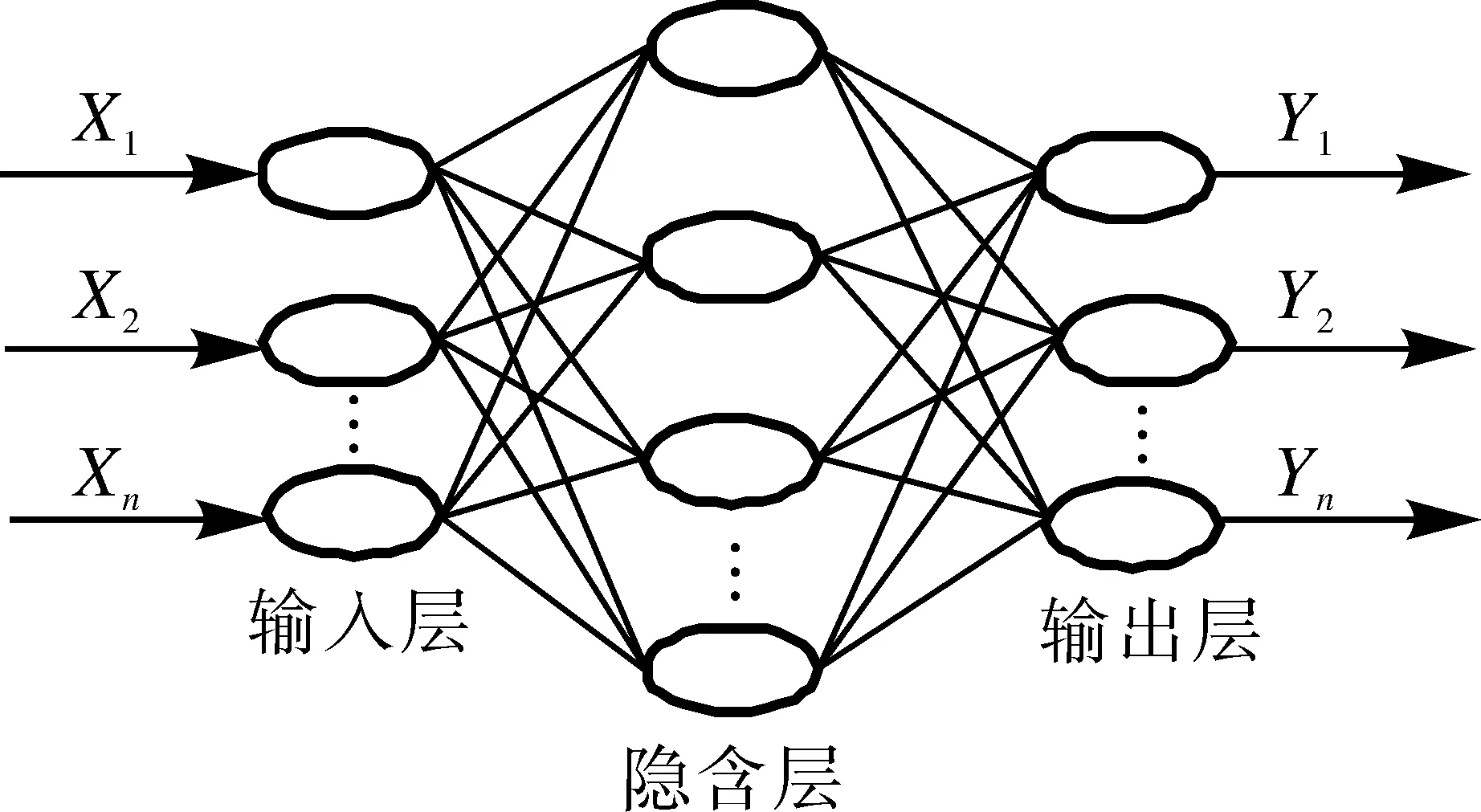
图1 BP神经网络结构图

正向传播过程中，训练样本从输入层传入，通过隐含层逐层处理后，传递给输出层。传递过程主要通过将上一层输出加权求和，随后通过传递函数转换作为下一神经元的输入，其表示式为：

(1)

(2)

式中：wij——输入层和输出层神经元之间的权值系数；

wjk——隐含层与输出层神经元之间的权值系数；

xi——神经元输入端；

aj、bk——隐含层和输出层阈值；

f——隐含层传递函数；

Hj——隐含层输出；

Ok——预测输出；

I——隐含层节点数。

本文隐含层传递函数选择具有光滑连续性质的Sigmoid函数，计算式为：

(3)

当实际输出与期望输出差别较大时，需进行误差反向传播分析，即根据神经网络的误差值更新正向传播的权值系数和阈值，并重新进行网格训练。其中，权值系数和阈值更新如下：

(4)

(5)

式中：ek——训练过程中的预测误差；

η——学习率。

基于上述分析，BP 神经网络的实现过程如图2所示：首先根据实际情况选择训练样本，并明确模型输入变量和输出目标，随后通过正向传播和反向误差传播训练网格，通过仿真测试验证是否达到目标精度，最后满足目标要求时输出预测结果。

图2 BP神经网络实现流程图

2 基于BP神经网络的加速度预测和行车舒适度评价流程及实现步骤

通过车桥耦合有限元分析模型获得训练样本，结合BP神经网络模型对输入样本进行网络训练，即可获得满足精度要求的车桥加速度预测模型，并在此基础上可对桥梁进行行车舒适度评价。具体来说，基于BP神经网络的加速度预测和行车舒适度评价流程如图3所示，实现步骤如下：

步骤1：通过有限元分析软件，并结合相关车桥耦合数值分析方法，建立正确合理的车桥耦合有限元分析模型。

步骤2：根据桥梁具体信息，选择影响较大的因素作为样本向量并生成样本点，通过有限元模型计算样本点对应的加速度信息，以此确定训练样本。

步骤3：将训练样本作为输入信息，通过BP神经网络模型进行网络训练，直至车桥耦合加速度预测模型满足精度要求。

步骤4：根据车桥耦合加速度预测模型，结合相关规范开展桥梁行车舒适度评价。

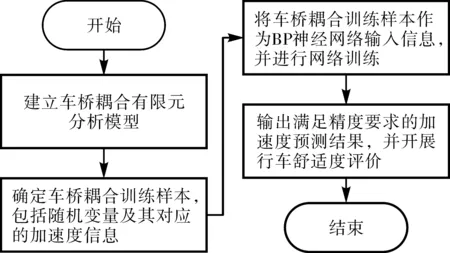
图3 基于BP神经网络的车桥耦合加速度预测及行车舒适度评价流程图

3 算例分析

3.1 车桥耦合有限元模型

本文以某典型工程中连续刚构桥为例，通过BP神经网络对该桥进行车桥耦合加速度预测分析以及行车舒适度评价。基于通用有限元软件ANSYS建立连续刚构桥车桥耦合有限元模型，其中桥梁纵向取三跨，跨径分别为50 m、70 m和50 m，横向桥宽为12.8 m，主梁采用单箱单室截面，长度和宽度分别为12 m和4.2 m。车辆模型选用两节车厢，每节车厢4对轮子，轨道数为1，采用工字型截面。

单元选用方面，桥梁采用SOLID65单元模拟，车辆采用SOLID 185单元模拟。边界条件和网格划分方面，对桥梁墩底和边跨设置为固定约束，并通过映射方法划分网格。连续刚构桥车桥耦合有限元模型如图4所示。车辆过桥速度设置为30 m/s，路面不平顺等级参考《机械振动道路路面谱测量数据报告》(GB/T7031-2005)[20]设置为B级，通过Newmark-β法分离迭代求解车桥耦合振动微分方程。

图4 车桥耦合有限元模型图

3.2 加速度预测结果

基于上述分析，进一步可得到基于BP神经网络的连续刚构桥车桥耦合加速度预测结果：(1)根据该连续刚构桥实际情况，选取主梁弹性模量E1、主梁容重γ1、主墩弹性模量E2和主墩容重γ2作为随机变量，并采取拉丁超立方抽样技术生成样本点；(2)通过Matlab调用车桥耦合有限元分析模型，计算各个样本点对应的加速度信息；(3)将各样本点及其对应的加速度信息作为训练样本，收敛误差设置为0.001，通过BP神经网络模型进行网络训练直至满足精度要求。

图5给出了预测得到的连续刚构桥加速度时程和数值模拟时程对比曲线。由图5可知，桥梁加速度时程均沿桥面上下波动，BP神经网络模型的桥梁预测值和数值模拟方法得到的结果在趋势和峰值上达到了高度吻合。表1给出了桥梁加速度预测值和数值方法结果的指标对比。由表1可知，数值方法得到的桥梁加速度均方根和最大值分别为0.291 57 m/s2和-0.480 76 m/s2，而BP神经网络模型预测方法的均方根和最大值为0.287 41 m/s2和-0.476 17 m/s2，与数值模拟的相对误差分别为1.43%和0.96%，表明本文方法可近似替代数值方法计算车桥耦合作用下的桥梁加速度。

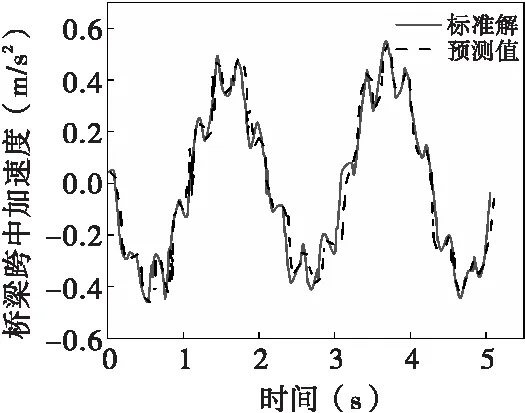
图5 桥梁加速度时程对比曲线图

表1 桥梁加速度时程指标对比表

图6给出了车桥耦合作用下，BP神经网络模型方法和数值方法得到的车辆加速度时程曲线。由图6可知，BP神经网络模型方法同数值方法的时程曲线基本吻合。两类方法的车辆加速度指标数据如表2所示。由表2可知，数值方法的车辆加速度均方根和最大值分别为0.110 13 m/s2和-0.190 62 m/s2，BP神经网络模型预测方法的均方根和最大值为0.108 83 m/s2和-0.196 50 m/s2，相对误差分别为1.18%和3.08%，说明本文方法亦可较好地预测车辆加速度信息。

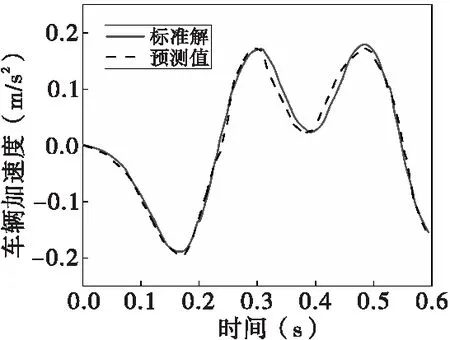
图6 车辆加速度时程对比曲线图

表2 车辆加速度时程指标对比表

3.3 行车舒适度评价

桥梁在服役过程中，可能存在坑槽、伸缩缝等结构损伤，当车辆行驶时可能发生剧烈振动。由于行车舒适性与桥梁加速度响应相关，为了评价司乘人员的舒适性，可根据本文得到的BP神经网络车辆加速度预测模型对桥梁进行行车舒适度评价。参考《人体承受全身振动评价指南》(ISO-2631)标准[21]，车辆加速度均方根和舒适度标准如表3所示。

表3 行车舒适性评价标准表

根据表3行车舒适性评价标准，由前文分析得到本文连续刚构桥车辆加速度均方根为0.108 83 m/s2，得到当车辆以30 m/s驶过该刚构桥时舒适度处于第一等级水平，司乘人员不会产生不舒适感，该桥具有较好的行车性能。

4 结语

本文基于BP神经网络提出了桥梁车桥耦合振动加速度预测及其行车舒适度评价方法，并以某连续刚构桥车桥耦合分析为例验证了本文方法的适用性。分析结果表明：本文加速度预测模型可近似替代数值模拟方法，其桥梁加速度均方根和最大值与数值方法相对误差分别为1.43%和0.96%，车辆加速度均方根和最大值与数值方法相对误差分别为1.18%和3.08%，同时对比ISO-2631标准发现，本文连续刚构桥具有较好的行车性能，行车舒适性处于一级水平，且本文方法简单可行，可极大地降低车桥耦合计算成本，具有一定的实用价值。