双侧电驱履带车辆模糊自适应滑模转向控制

魏 琼，金 鹏，张道德，周 刚，胡新宇

(湖北工业大学 机械工程学院， 湖北 武汉 430068)

0 引言

电传动履带车辆较液力机械传动具有结构简单、传动效率高的优势，但双侧独立电驱履带车辆行驶时阻力受行驶状态、路面参数等因素影响，呈现非线性、不确定动态变化，转向过程中存在控制一致性差、转向响应慢等问题[1-4]，因此设计优良的转向控制算法对提高履带车辆运动性能尤为重要。

目前，国内外针对车辆转向运动控制进行了大量的算法和控制结构研究，极大地提高了双侧电驱动履带车辆的转向性能。文献[5]设计了驱动控制方案和算法，提出了调速和转矩调节控制策略，在不同工况下的仿真结果验证了两种控制策略的可行性和有效性。文献[6-9]提出了一种基于模糊比例-积分-微分(proportion-integration-differentiation,PID)算法和反向传播(back propagation,BP)神经网络的转向控制策略，以提高转向系统的动态响应能力。驾驶员的转向意图被解析为内部电机制动扭矩。文献[10]采用模糊自适应算法对车辆转向进行控制,通过“轨迹-角度-电流”3层模糊自适应PID算法输出电子助力转向(electric power steering,EPS)系统控制信号，提高了转向的稳定性和准确性。文献[11]提出了一种基于模糊控制的转向补偿控制策略，该策略以踏板、方向盘和变化率信号为输入变量，以提高转向灵敏度。文献[12]以双电机耦合电传动履带车辆为对象，设计了一种解耦的速度-横摆角速度控制结构，研究了滑模控制算法，实现了解耦条件下的稳定转向控制。上述研究大都采用基于稳定速度下的车辆转向控制方法，未对全范围速度下的车辆转向进行良好的控制。本文基于上述研究，提出了一种基于模糊自适应调节的滑模控制,有效地降低了滑模抖振,同时具备响应速度快、抗扰动能力强的优点，能够实现履带车辆的稳定转向。

1 双电机独立驱动履带车辆模型

以KOMODO-01通用型履带车辆为例，该车型具有通过性强、重心低、运行平稳的优点。其内部搭载高扭矩无刷直流电机，两侧主动轮分别由电机单独驱动。履带车辆实际转向过程较为复杂，为了突出转向过程的不确定性问题，考虑履带车辆行驶时影响其稳定性的主要因素，忽略车辆行驶时空气阻力和悬架系统的影响，基于理论转向进行分析，对履带车瞬态转向作出如下假设：(Ⅰ)履带车辆质心与形心重合；(Ⅱ)履带车辆接地部分法向载荷分布均匀；(Ⅲ)转向过程中忽略内外侧履带的滑移和滑转。履带车辆运动学及动力学模型如图1所示。

图1 履带车辆运动学及动力学模型

履带车辆转向过程按转向半径划分，不同转向半径下两侧电机输出力矩有所不同，有3种转向工况[13]。设R为履带车辆转向半径，Rf为履带车辆自由转向半径，B为履带中心距。相对转向半径ρ=R/B，ρ>ρf时为大半径转向；0<ρ≤0.5时为小半径转向；0.5<ρ≤ρf时为中半径转向[14]。由于大半径转向时工况与中半径转向近似，同时中半径转向时两侧电机工作较为复杂，本文对中半径转向工况进行分析。

图1中，F1和F2分别为履带车辆牵引力与制动力，Ff1和Ff2分别为两侧履带受到的摩擦阻力,Fq和Fh为车辆所受横向阻力，Mμ为转向阻力矩，T1和T2为两侧电机输出力矩，v1和v2为两侧履带速度，vc和ωc分别为履带车辆的车速及转向角速度，o为转向中心，c为车辆质心。

对转向过程分析，将车辆的转向分解为横向摆动和纵向平移运动，推导出履带车辆两侧履带所受外力及外力矩，以及电机提供的牵引力及制动力，建立转向动力学模型。根据假定条件，车辆受力及所受力矩表达式为[15]：

(1)

其中：i为减速器传动比；η为电机轴至履带的传动效率；f为地面阻力因数；L为履带接地长；μ为转向阻力因数。

履带车辆实际转向是一个非稳态过程，设Fd为不确定性纵向阻力，Md为不确定性阻力矩，J为转动惯量，根据履带车辆动力学模型推导出履带车辆动力学方程为[16]：

(2)

将式(1)代入到式(2)中可得：

(3)

2 转向控制系统分析与算法研究

本文研究的履带车辆采用遥控器进行车辆运动控制，对于整个控制系统，输入信号为遥控器的车体直行与转向通道2通道信号。解析为摇杆油门信号和转向信号，暂不考虑制动信号，均为比例控制。为了实现对履带车辆的闭环控制，对油门信号和转向信号进行解析，对应得到履带车辆的行驶速度和转向角速度[17]。根据已知的油门信号，解析为履带车的目标车速，解析公式为：

(4)

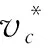
同理，将摇杆转向信号解析为转向角速度，解析公式为：

(5)

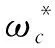
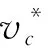
图2 整车控制系统结构框图

(6)

设Kp为控制量增益矩阵的变换矩阵，控制器输出控制量为u1和u2，则控制量与电机输出力矩关系为：

(7)

车辆转向时车速和转向角速度呈非线性的变化，滑模变结构控制(sliding mode control，SMC)算法能够实现带有不确定性和未知外干扰的非线性系统鲁棒控制[18]，因此，本文采用SMC算法结合模糊自适应算法重新设计控制器，对传统的滑模控制进行改进，并利用仿真模型进行与PID算法的对比验证。

2.1 车速滑模变结构控制器设计

车速控制的核心在于对期望信号的快速跟踪以及克服路况变化，增强对扰动的鲁棒性[19]。滑模控制能够有效地克服扰动，但容易出现较大的稳态误差，本文在滑模控制算法中引入积分项，可以降低跟踪车速信号的稳态误差，提高行驶的稳定性。根据式(6)，车速控制子系统的状态方程为：

(8)

引入积分项可以得到积分滑模面：

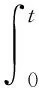
(9)

控制律设计为：

u1=ueq+usw，

(10)

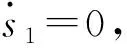
(11)

usw为切换控制量，理想的滑模控制律常采用符号函数，然而在实际的滑模变结构控制中，滑动模态呈抖振形式，所以采用饱和控制函数替代符号函数。设δ1为切换增益，ε为边界层厚度，则有：

usw=δ1sat(s1/ε),δ1>0。

(12)

根据式(10)、式(12)和式(13)可得设计的滑模控制律为：

(13)

证明(Ⅰ)当s1≥ε1时，滑模在边界层外，sat(s1/ε1)=sgns1，

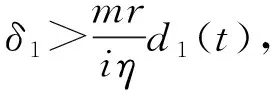
(Ⅱ)当s1≥ε1时，滑模在边界层内，sat(s1/ε1)=s1/ε1。

2.2 转向角速度自适应模糊滑模控制器设计

转向角速度控制的核心问题是对目标转向角速度的快速跟踪，以及适应转向阻力的非线性变化和克服不确定扰动，实现稳定转向。履带车辆转向过程受转向半径、履带车速以及路面参数变化影响较大，其中地面转向阻力难以进行定量的数学分析，所以引入模糊自适应控制项期望对转向阻力进行在线逼近，保证控制系统的适应性和控制精度；结合滑模控制，提高系统的鲁棒性，同时通过模糊控制项柔化控制信号，减小滑模抖振[19-20]。转向角速度控制系统原理如图3所示。

图3 转向角速度控制系统图

根据式(6)，转向角速度控制子系统的状态方程为：

(14)

(15)

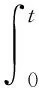
(16)

控制律设计为：

u=ueq+usw，

(17)

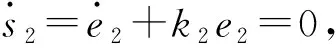
(18)

采用模糊自适应算法，模糊自适应项对未知的地面转向阻力因数进行逼近，以提高精度。令f(s)=μ，根据模糊逼近理论，采用径向基函数对μ进行逼近。

μ=a*Tξi(s)+δ2，

(19)

其中：a*为最优权重向量；δ2为逼近误差，满足|δ2|≤β,β>0；ξi(s)为模糊基函数向量，ξi(s)满足：

(20)

采用单模糊输入系统将切换函数作为模糊数输入，减少模糊规则的数量，采用高斯隶属度函数，可得：

(21)

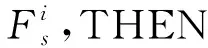
(22)

根据模糊逼近理论，可调参数ai最优时，存在一个最优参数估计值逼近μ*，假设最优参数估计值为：

(23)

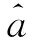
(24)

对于自适应算法的逼近误差，设计切换控制算法usw来消除，可得：

usw=-βsat (s2)，

(25)

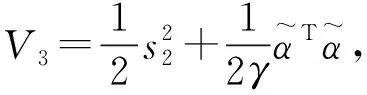
当s1≥ε1时，滑模在边界层外，sat (s1/ε1)=sgns1。

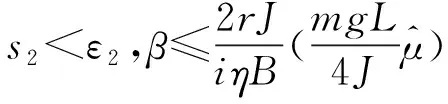
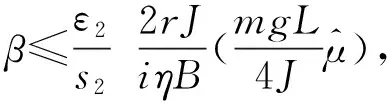
3 仿真分析与实验验证

为了验证本文所设计的履带车辆转向控制方法的可行性及控制性能，基于履带车辆动力学模型及控制算法，在MATLAB/Simulink软件中进行仿真验证。其中，控制器各项参数：车速控制器中k1=0.36,δ1=20,ε1=0.6；转向角速度控制器中k2=200,ε2=0.2，β=120，γ=180；最大阻力因数μmax=0.8。双侧电驱履带车辆主要技术参数如表1所示。

表1 实验履带车基本参数

仿真实验中设计了PID控制和SMC算法进行不同速度下不同工况转向控制对比，其中履带车辆输入信号如图4所示。斜坡信号输入时履带车辆的车速跟踪曲线如图5所示，对于渐进加速的前进和转向运动，PID控制在跟踪速度时会出现3%～11%的超调,SMC算法则能够迅速达到稳定且无明显超调；且PID控制存在0.2～0.5 s的时滞，SMC算法则能够较为精确地跟踪到期望信号。

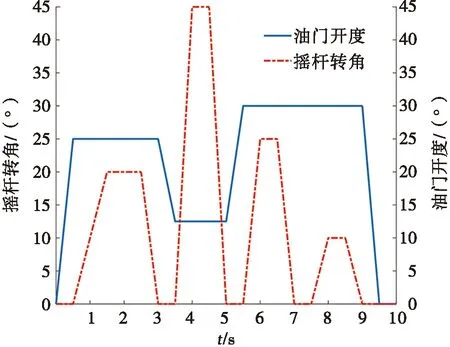
图4 履带车辆输入信号

改变输入信号为阶跃输入，进行了履带车辆转向实验验证，结果如图6和图7所示。3 s时履带车辆第1次转向,目标车速0.5 m/s,目标转向角速度0.24°/s；6 s时第2次转向，目标车速0.1 m/s，目标转向角速度0.145°/s。采用了PID控制和SMC算法进行对比，对于车速的跟踪，两种算法都能够较为精确的跟踪到期望信号，但是PID控制存在约1 s的时滞,SMC算法则能够迅速达到稳定且无明显超调。对于转向角速度的跟踪，PID控制出现超调或难以达到稳态，无法精确跟踪期望值。SMC算法能够抑制扰动和克服路面不确定因素的影响，超调量只有4%，在车辆变速时也能够稳定转向，精确跟踪期望值，车辆行驶速度与转向角速度跟踪响应速度较PID控制分别提高了1.9 s和0.5 s,且没有出现较明显的抖振和静差。

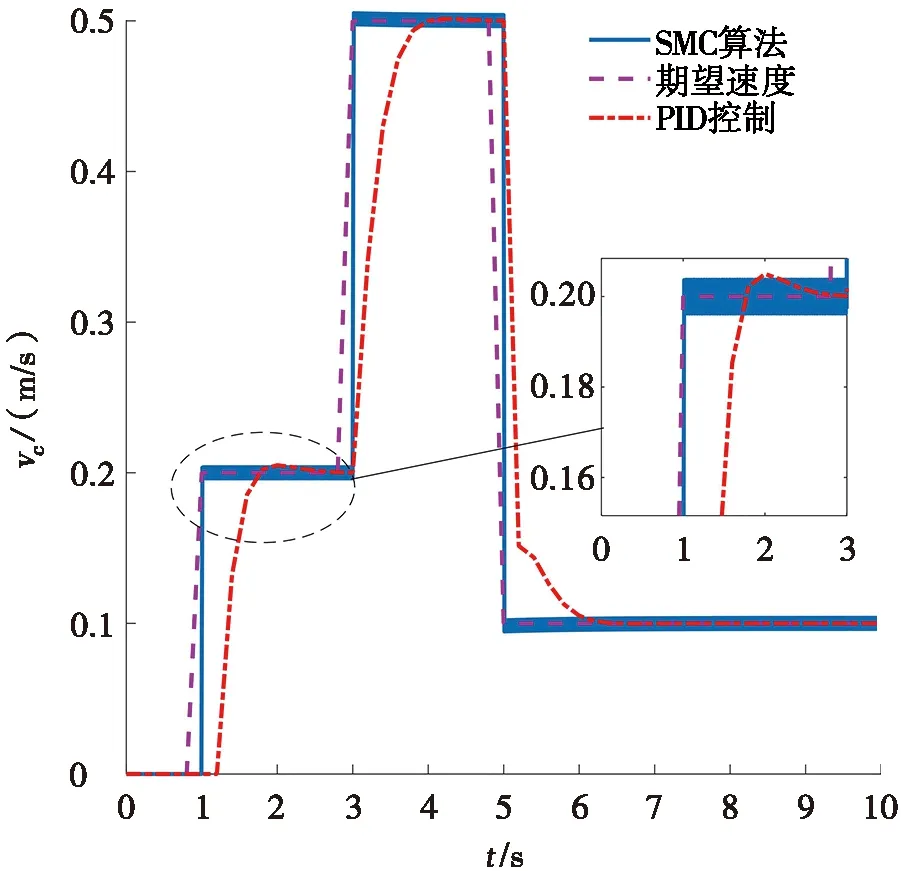
图6 阶跃输入时履带车辆速度曲线

4 结论

本文以双侧电驱履带车辆作为研究对象，并对其转向过程进行了仿真分析，将存在耦合关系的车辆转向运动控制系统转化为两个单输入单输出的子系统，消除了耦合作用。在等效控制的基础上，引入积分滑模项和模糊自适应项，分别用于车辆转向时的车速及转向角速度的控制。提出的算法能够根据转向时车辆速度以及角速度的不同特性进行精确跟踪，且响应较快，抗扰动能力强，可以满足实际转向工况中对履带车辆的控制需求。