蒙特卡洛法合成的风扇能效测试不确定度评定
2022-11-17赵一帆程银宝王学影
赵一帆,程银宝,吴 军,罗 哉,王学影
(1.中国计量大学 计量测试工程学院,浙江 杭州 310018;2.安徽省计量科学研究院,安徽 合肥 230051)
0 引言
家用电器数量的迅速增长,不仅带来巨大的能源消耗,也加重对环境的污染,中国在提高家用电器的能源效率、落实能效标识管理方面尤为重视[1]。研究对象风扇为典型的能效标识管理产品,单个产品虽小,但销量高,耗能量加起来不可忽略,对于其能源效率的测量与评定可以检验其是否符合标准[2]。
目前,文献[3]依据国家标准[4]假设各测量点输出风量为强相关,对风扇能效测试进行评定,但是测量不确定度表示指南(guide to the expression of uncertainty in measurement, GUM)方法在处理测量模型非线性、输入量具有相关性等测量系统的不确定度评定时存在一定的不足[5-6],评定结果可信度不高。文献[7]通过分析影响电风扇风量测试结果的因素,认为各点测量风速值相互独立,只对风量测试系统进行评定,没有对其能源效率进行分析。基于蒙特卡洛方法(Monte Carlo method, MCM)[8]进行复杂系统的不确定度评定能有效解决上述难题。MCM法是通过概率分布影响不确定性输入的先验信息来进行评定,可有效弥补GUM方法的局限性[9-10],同时对GUM方法的适用性进行验证。文献[11]基于计算机模拟的优势,利用MCM对A类评定方法进行验证,分析A类评定中3种方法的可靠性程度。文献[12]利用MCM对动态测量进行评定,其测量模型的输入量是非线性的,利用MCM评定可避免非线性模型的干扰。本文在交流电风扇的风量测量和能源效率测试的基本原理上,采用两种方法分别对风扇能效测试系统的风量值和能效值的试验结果进行测量不确定度评定,以验证风量测量不确定度评定时是否考虑各测量点风速的相关性。
1 测量方法
在试验过程中,选用精确度等级为0.3级的功率计获取风扇的功率值,将两台风速仪放置在扇叶轴线两侧,并与扇叶轴线上的的水平导轨垂直,测量前,设置风扇起始位置位于风速仪的0.02 m处,通过伺服电机带动风速仪向后移动,为了精准评定,测量间距设定为0.04 m。
以直径为300 mm的落地扇进行测试,实验室的环境温度应为(20±3)℃,为了使试验效果显著,选择最高转速档位的风速值作为能效值测量的输入风量,保持风速方向不变。试验开始前,进行预热运转,试验过程中,风速仪的叶片与被测试电风扇的扇叶应相互平行,保持风扇轴心线与风速测量仪正中心在同一水平线上,直线导轨控制风速仪向后移动,直到所测得的平均风速低于 0.4 m/s时为止。
2 测量模型
各点在n秒测量期间,采集到的风速值用Vi来表示,则风速的计算公式为[13]:
(1)
其中:VL为左边风速仪测量的风速值,m·min-1;VR为右边风速仪测量的风速值m·min-1;vi为每秒采集的风速值m·min-1。
定义测量点i处的平均风速Vi,用测得的左、右风速的均值来表示,
(2)
总输出风量是风速值不低于限度的所有圆环面积的总风量和,测量总风量F的数学模型为[13]:
(3)
其中:Vi为测量点i处的平均风速,m/min;Si为测量点i处的圆环的面积,m2,Si=2πrid;ri为测量点i处圆环的半径,m;d为各测量点的圆环宽度,由试验时风扇扇叶的长度决定,试验取0.04 m。
能源效率的数学模型为:
(4)
其中:η为试验所得能效值,m3/(W·min);F为试验测得的总风量,m3/min;P为电动机的输入功率,W。
3 风量测量的不确定度评定
依据上述数学模型,试验得到的部分测量数据以及偏导数列见表1。
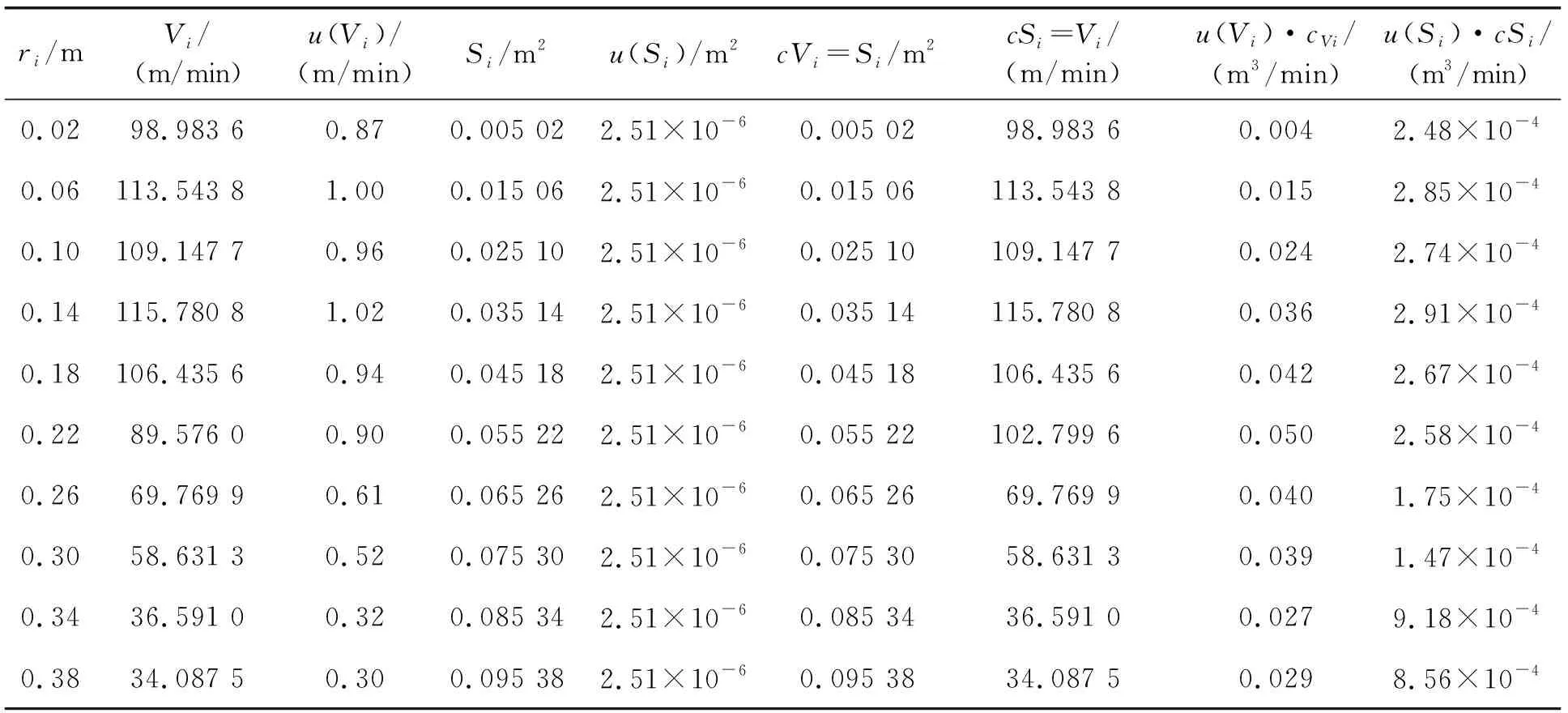
表1 试验测量得到的数据
3.1 GUM方法评定
3.1.1 风量测量重复性引入的不确定度分量
对输出风量进行10次独立重复测量,测量结果分别是:34.715 6 m3/min,34.805 7 m3/min,35.018 8 m3/min,34.805 4 m3/min,35.024 8 m3/min,34.704 7 m3/min,34.841 5 m3/min,34.822 8 m3/min,依据贝塞尔(Bessel)公式计算风量重复性引入的不确定度分量为:
(5)
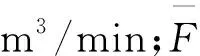
3.1.2 风速仪引入的不确定度分量
风速仪的相关资料中给出Urel=2.5%(k=2),由两台风速仪组成的风速测量系统的相对不确定度为:
(6)
① 假设左右风速仪测得的平均风速为强相关。
强相关时,相关系数rij=1,则风速测量相关时引入的标准不确定度分量公式为:
(7)
式(7)经过化简后,将表1中的数据代入式(8),风速仪测量强相关时引入的不确定度分量为:
(8)
② 假设左右风速仪测得的平均风速为独立不相关。
不相关时,相关系数rij=0,将表1中的数据代入式(9),风速仪测量不相关时引入的不确定度分量为:
(9)
3.1.3 圆环面积引入的不确定度分量
风速仪探头导轨的校准证书中给出Urel(L)=2×10-5m (k=2),测量点i处圆环平均半径ri的标准不确定度为:
(10)
已知Si=2πrid,单位m2。在测量点i处圆环面积Si引入的标准不确定度uB(Si)为:
(11)
则圆环面积测量引入的不确定度分量为:
(12)
3.1.4 风量测量的合成标准不确定度
将上述不确定度分量进行合成,当左、右风速强相关时,u1(F)=0.32 m3/min;当左、右风速无关时,u2(F)=0.13 m3/min。
3.2 MCM评定
蒙特卡洛方法[14]是通过计算机模拟对输入量进行离散随机抽样,利用测量模型传递输入量的概率分布,获得输出量的特征信息,适合多个输入量、单一输出量的模型[15]。在已知输入量的概率密度函数(probability density function, PDF)分布下,可预测到输出量的实际分布[16]。利用蒙特卡洛方法模拟服从期望为各输入量的测量值,方差为各输入量服从概率分布的随机数,从而进行不确定度评定[17]。 操作步骤如下所示:
(Ⅰ)构造测量模型。分析所求问题的原理,考虑测量过程中的主要误差来源,建立恰当合理的不确定度评定模型Y=f(Xi)[18]。
(Ⅱ)输入量的抽样。测量模型确定后,利用已有信息、试验数据、相关的计量学知识,基于贝叶斯(Bayes)原理或最大熵原理,设定输入量Xi的概率密度函数。选择试验样本量的仿真次数M,对输入量Xi抽样M次,扩大样本量,常见的概率分布有矩形分布、正态分布、三角分布、t分布和反正弦分布[19-20]。依据实际情况,判断输入量服从的分布类型,多数情况下默认服从正态分布。
(Ⅲ)输出量的模拟。输出量Y分布函数的确定,主要是将抽样后的输入量Xi代入测量模型,得到M个输出值及其分布函数信息,对得到的M个输出值严格按照递增顺序排序,绘制出频率分布直方图[21]。结合包含概率给定包含区间,判断其分布类型,得到其相关特性,比如估计值和标准不确定度。
测量结果的估计值按式(13)计算:
(13)
标准不确定度按式(14)计算[22]:
(14)
由式(3)分析可知,总风量F与Vi、Si有关,而Si与ri有确定的关系,故对Vi,ri的PDF进行设定。
3.2.1 测量点i处平均风速Vi
根据最大熵原理,Vi设为正态分布,输入量风速测量得到10组数据,测量点是彼此独立的,针对每点逐一进行PDF设定,求出各测量点平均风速的期望值和标准差,即V1~N(98.983 6,0.872),V2~N(113.543 8,1.002),…,V10~N(34.087 5,0.302),分别对各个组测得的Vi在设定的样本量下进行大样本抽样,得到Vi的M个随机数值,V1,V2,…,VM。
3.2.2 测量点i处平均半径ri
由式(10)可知,ri的标准不确定度已计算出,为0.000 01 m。根据最大熵原理,确定概率密度函数,ri设为正态分布,则r1~N(0.02,0.000 012),r2~N(0.06,0.000 012),…,r10~N(0.38,0.000 012)。得到ri的M个随机数值,r1,r2,…,rM。
对输入量取样设定,依据MCM评定步骤,利用MATLAB软件[23]对数学模型中的输入量ri、Vi进行M=1×106次随机模拟抽样,并根据总风量F测量模型,将各点总风量抽样后累加计算得到M=1×106个输出量,将测量结果从小到大递增排列,绘制出总风量的频率分布直方图,如图1所示。
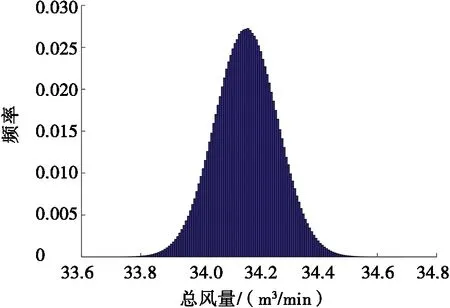
图1 总风量概率分布直方图
4 能源效率测量的不确定度评定
4.1 GUM方法评定
4.1.1 电能量测量引入的不确定度分量
对输入功率进行10次独立重复测量,测量结果分别为:32.7 W、32.5 W、32.7 W、32.9 W、32.7 W、32.7 W、32.6 W、32.7 W、32.8 W、32.7 W。风扇能效值A类标准不确定度引入的不确定度分量为:
(15)
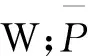
功率计的校准证书给出U=0.08%(k=2),且试验的电能量测量示值P=32.7 W,则由电能量测量引入的B类标准不确定度分量为:
(16)
则合成的标准不确定度为:
(17)
4.1.2 总风量测量引入的不确定度分量
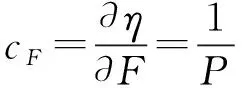
4.1.3 能效测量的合成标准不确定度
根据方差合成定理将总风量和功率的不确定度分量合成,能源效率的标准不确定度为:风量不相关时u1(η)=0.009 8 m3/(W·min);风量相关时u2(η)=0.004 3 m3/(W·min)。
4.2 MCM评定
能源效率依赖两个互相独立的输入量:P、F。由式(17)可知,P的标准不确定度为0.06 W。根据最大熵原理,为P设定正态分布P~N(32.7,0.062),风量测量的概率分布以及不确定度在3.2节中已求出,将其代入到能源效率测试模型中,利用数据模拟软件对数学模型中的输入量进行M=1×106次随机模拟抽样,根据公式计算得到M=1×106个输出量,能效值按递增顺序排列绘制出频率分布直方图,如图2所示。
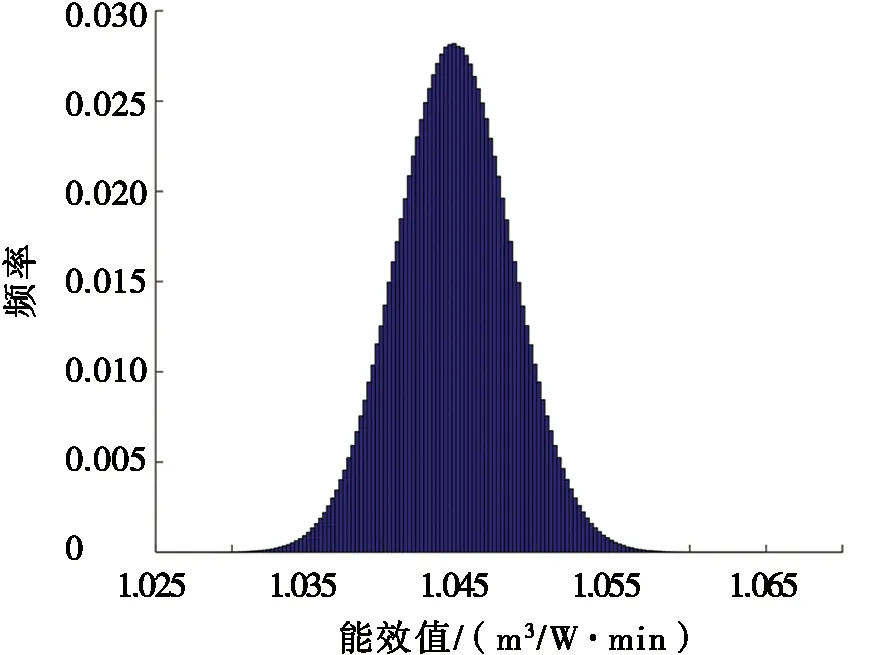
图2 能效值概率分布直方图
4.3 试验数据分析
由以上数据分析可知,圆环面积引入的不确定度分量与重复性及风速测量引入的不确定度相比影响较小,可以忽略。经典GUM方法中输入量相关性的两种假设的评定结果,与MCM的评定结果进行比较,结果如表2所示。由表2可知:MCM得到的风量的不确定度和能效测试的不确定度,与GUM方法评定时假定左、右风速仪测得的各点平均风速不相关的评定结果接近。
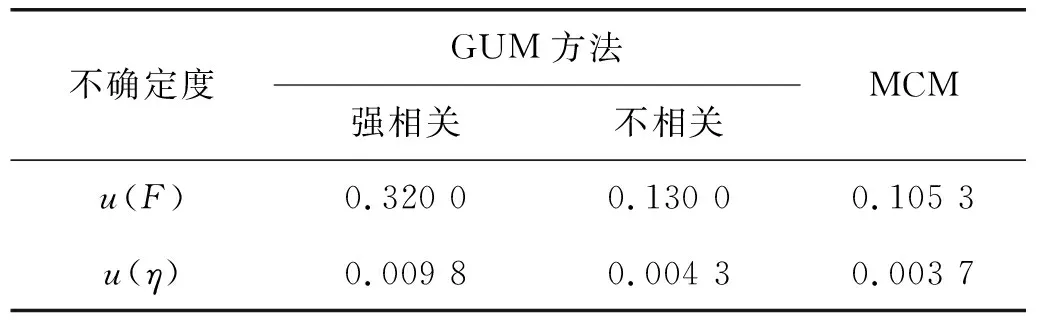
表2 GUM与MCM评定方法得到的结果比较 m3/(W·min)
5 结论
(1)MCM得到的能效不确定度0.003 7 m3/W·min,更靠近各测量点平均风速不相关时的能效不确定度0.004 3 m3/W·min,表明各测量点平均风速不相关。
(2)运用GUM方法对测量模型进行评定时,无法判定左、右风速是否相关,如若假设为强相关时,会使得能效的不确定度偏大,可靠性不高。
(3)通过MCM和GUM方法进行分析,可以看出MCM计算简便,通过编程易于实现,无需考虑输入量相关性、模型非线性的影响,运算过程简便,评定复杂模型时更快速、可靠。
