素养为先:论始于“学生自主创造”的主题探究教学*
2022-11-17210003南京师范大学附属中学孙风建
210003 南京师范大学附属中学 孙风建
《普通高中数学课程标准(2017年版)》明确了数学学科的核心素养,希望教师能把握数学本质,重视情境创设和问题提出,从整体规划学生的核心素养发展.主题式教学可以很好地承载“整体性”学习目标.主题探究教学本质在“主题”,由学生鲜活的思考或疑惑生长出的探究主题,有利于学生发挥主动性,自主推动探究,在不断提出和解决问题过程中发展高阶思维.
函数是高中数学中一个十分重要的概念,如果学生没有充分经历函数概念的抽象过程,往往很难在千变万化的函数问题中应对自如,笔者以“这样的函数有多少个”这一主题的探究教学为例,以学生素养为先,研究教学.
1 “这样的函数有多少个”主题探究教学过程
1.1 激发动机,生成探究主题
在函数这一章节中,苏教版教材给出了这样的问题:已知一个函数的解析式为y=x2,它的值域为[1,4],这样的函数有多少个?
这是一个开放性问题.学生通过之前学习的知识(即函数的三要素决定一个函数),很快发现本题中对应法则和值域已限定,要确定函数,关键在于确定定义域.如果定义域稍加变化,就可以得到一系列答案,如x∈[1,2],x∈[-2,-1],x∈[1,2]∪[-2,-1]等,所以答案是“无数个”.
表面来看,学生已经掌握函数概念.如果仅止于此,可能就错过了一个让知识整体关联的好机会.所以,笔者随即追问:如果对应法则不变,值域变化了,这样的函数有多少个?学生发现其中暗藏玄机,一时难以简单回答,决定一探究竟,随即诞生了一个探究主题——“这样的函数有多少个”.
1.2 自主合作,形成初步方案
学生分成小组,从确定对应法则出发,探索如果改变值域,结果会发生怎样的变化,其中有什么一般特征,形成了本组的自主探究任务.有的小组尝试把值域换成其他有限数,最终探索出了值域为一般有限区间[a,b]时的情况.有的小组尝试把连续区间离散化,但情况太多,探索得出普适的结论存在困难,经过讨论,决定从最简单且和[1,4]形式最接近的情况{1,4}入手探究.
自主探究1已知一个函数的解析式为y=x2,它的定义域和值域均为[a,b],则这样的函数有多少个?


(3)当a<0 综上,这样的函数只有1个. 自主探究2已知一个函数的解析式为y=x2,它的值域为{1,4},这样的函数有多少个? 解法1:当y=1时,x=1或x=-1;当y=4时,x=2或x=-2.以函数定义域中的元素个数来分类. (1)当元素个数为2时,有{1,2},{1,-2},{-1,2},{-1,-2},共4种; (2)当元素个数为3时,有{1,2,-2},{1,-1,-2},{-1,1,2},{-1,1,-2},共4种; (3)当元素个数为4时,只有{1,-1,2,-2} 1种. 因此,这样的函数有9个. 解法2:当y=1时,x=1或x=-1;当y=4时,x=2或x=-2. 第一步有三种选择,即x可以是1或-1,也可以是两个都取,共有三种不同的选法;同理,第二步也有三种不同的选法,按照分步计算原理共有九种. 随着集合元素的增多,要清晰准确地数出函数个数变得越来越困难,有的学生苦于列举法情况太多,也有学生想尝试用排列组合的方法计数,却难列举清楚.教师的适时引导显出了必要性.但“引导”不等同于“告知”,学生的思维处于活跃状态时,前期探索激活了最近发展区,这时恰当的启发性问题可确保学生有充分的思考空间. 启发1探究1的方法有什么优势?探究2里的两种方法又各有什么优势? 学生反思成果:(数学思想)具体区间不胜枚举,但数学不满足于“逐个列举”研究函数,而是观察具体事实的共同特征,进行抽象概括得到一般性结论,这样的结论具有普适性,自然可包括具体区间的种种情况. 启发2如果让你继续探索,你会从什么角度研究? 基于对探究1的反思,大部分学生会倾向于探究其一般性结论.随着讨论深入,学生的思路越来越发散,有的组提出希望找出这个集合的规律,将其扩充,尝试探索更一般的情况值域为{1,4,9,…n2}.还有的组认为可以结合集合部分的知识进行综合探索,比如探索值域为{1,4,9,…,n2}的非空子集,于是产生了综合性更强的两个探究角度. 自主探究3已知一个函数的解析式为y=x2,它的值域为{1,4,9,…,n2},这样的函数有多少个? 解:根据函数定义,值域中的每个元素在定义域中都有唯一的元素与之对应,所以与1对应的元素可以有1,-1,也可以是两个元素都取,共有三种情况.同理,与4对应的元素也有三种情况,以此类推,根据乘法计算原理共有3n种情况,即这样的函数共有3n个. 自主探究4已知一个函数的解析式为y=x2,它的值域为{1,4,9,…,n2}的非空子集,这样的函数有多少个? 解法2:根据函数定义,值域中每个元素在定义域中都有唯一的元素与之对应,如与1对应的元素可以有1,-1,也可以是两个元素都取,当然也可以都不选,因此共有四种情况;同理,与4对应的元素也有四种情况.以此类推,根据乘法计算原理共有4n种情况,但是要防止与值域中每一个值对应的两个元素都不选这种情况发生,因此这样的函数共有4n-1个. 教师点评:在研究新问题遇到困难时,从特殊的情况开始摸索,通过总结类比和严格的逻辑推理,探索解决一般情况的方法,这也是数学探究的重要思想之一——化归思想. 启发3如果定义域也受了限制,我们又该怎样研究呢? 由图1可见,灰渣脱色率随吸附剂投放量加大而增加,投放量达到 1.5g·L-1时变缓,达 2.5g·L-1时进一步变缓。初期染液中有机物浓度较大时,吸附剂的吸附位与吸附质接触机会多,吸附效果好,当吸附质浓度小于某一浓度范围后,吸附剂的吸附位与吸附质作用几率降低,吸附效果减弱[5,6]。综合考虑,确定灰渣吸附剂投放量为2.5g·L-1为宜。 随着问题提升到一个新的难度,学生需要更多的思考时间,边探究边总结反思,有的组需要教师的点拨.经过讨论后各组达成共识:限制条件调整为“值域为定义域的子集”,同时函数的解析式也发生变化等. 自主探究5已知函数f(x)=x3-3x定义域为[a,b](a,b∈Z),若函数f(x)的值域为[a,b]的子集,则这样的函数有几个? 解:因为f(x)=x3-3x,所以f′(x)=3x2-3=3(x+1)(x-1),当x∈(-∞,-1),(1,+∞)时,f′(x)>0,当x∈(-1,1)时,f′(x)<0.所以f(x)在(-∞,-1)上单调递增,在(-1,1)上单调递减,在(1,+∞)上单调递增. (2)当a≤-1且-1 (5)当-1 因此,所求整数a,b的值为a=-2,b=2.这样的函数只有1个. 如表1所示,“这样的函数有多少个”主题式探究教学中,学生逐步生成了“特定值域区间-集合知识融合-一般定义域和值域-封闭函数”的探究路径,进行了一次从“事实到概念”的深入学习,从另一个角度又经历了一次核心概念的整体抽象过程.事实上,学生从特殊元素入手完成了探究2和探究3,之后对值域进行一般化,才发现探究1这样一个隐藏的探究路径,进而将思维拓展到了探究5这样一种更抽象复杂的层面,学生的深入思考无意间引发了一些新函数的定义,从而探究更抽象的数学对象,这是学生深入思考自然推动的结果,虽然对思维水平要求更高,但是整个过程却更加自然. 表1 “这样的函数有多少个”微主题式探究框架 学生能将函数、集合、分类计数原理、导数、不等式等知识有机结合,在探究和小组合作过程中激活最近发展区的相关知识,从研究一般问题“退”到从“特殊”入手,再从“特殊”问题“进”到一般情况完成更加严格的分析和表述,数学思想也在反思和总结环节得到凸显和加强.结合SOLO评价标准发现,学生思维从对问题单一层面的认知水平逐步提升至将多个知识层面有机融合的“关联结构水平”,并在对定义域和值域充分讨论后得到封闭函数这一更加抽象的认知,思维达到高阶的“拓展抽象结构水平”.由于本案例主题探究的起点为教材原题,学生并未表现出思维混乱、无序的“前结构思维状态”.开放探究的过程中学生研究热情高涨,数学核心素养的发展也得到了落实. 核心素养不是直接由教师教出来的,而是在问题情境中借助问题解决的实践培育出来的.日常教学中,教师应善于抓住学生思考过程中自主探究的“珠”,因势利导串成主题探究的“链”,自然诱发深度思考.同时以“启”促“发”,站在章节、模块甚至数学课程的高度去认识教学内容,从而形成有生命力、有灵魂的整体知识,激活数学知识间的关联性,为学生深度思考创造条件.问题解决的探究过程中,应始终坚持学生的主体地位,通过非“告诉”式的“引导”,让学生适时拓宽思路,变换探索路径时依然能清晰地把握核心对象,自主将重要概念与探究主题建立联系,发展数学核心素养. 随着学生知识储备的增加,以及教师在日常教学中对一些数学思想进行渗透,学生会喜欢这种“高屋建瓴”地建构知识体系的感觉,从而在自主和自觉的思考中实现思维跃变,对具体知识的认知也将提高至高阶水平.1.3 启发反思,促进深入研究
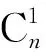
1.4 深度思考,提升抽象思维
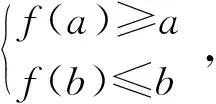


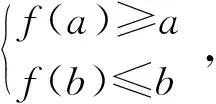
2 反思:素养为先,反观学生思维能力的培养