寒区高吸力非饱和土的破坏准则研究

宋锦坡， 崔宏环， 胡淑旗， 高鹏飞

（1.河北省土木工程诊断、改造与抗灾重点实验室，河北 张家口 075000；2.河北建筑工程学院，河北 张家口 075000）

0 引言

冀北山区由于季节的变化受到周期性冻融循环的影响。初春时温度开始回升，冻土中的冰逐渐融化蒸发，而该地区又位于400 mm等降水线上，降水较少，长时间干旱，造成边坡土体常年处于高基质吸力状态。这种冻融与高吸力的共同作用会导致路基边坡时常因拉剪强度不足而发生浅层滑坡。非饱和土可大体分为以毛细作用为主和吸附作用为主的两种状态（吸力值在1 500 kPa以下，为较低吸力范围，低吸力非饱和土中吸力是以毛细作用为主，而高吸力非饱和土中吸力主要是以吸附作用为主的［1］）。吸附作用主要是指土体中固-液相间的双电层作用力、范德华作用力和其他水合作用，多与结合水相对应。一般来讲，颗粒间的吸力越大胶结强度越高，非饱和土抵抗拉张应力的能力越强。吸力对抗拉强度的影响，虽然已有前人研究表明，由吸力引起颗粒间的吸附作用是非饱和土抗拉强度的一个重要组成部分［2-6］，但目前对高基质吸力范围下非饱和土抗拉强度的研究还太少，某些细节研究不够透彻。

近几年，有关冻融对抗拉抗剪强度的研究有很多，如黄星等［7］通过劈裂试验间接得出冻土的抗拉强度随负温的降低逐渐增大。Zhou等［8］基于巴西劈裂试验探究冻土内冰的含量对抗拉强度的影响，结果表明冻土的抗拉强度与冻土中冰的含量紧密相关。刘华等［9］对酸污染原状黄土进行抗拉试验，得出在经历冻融3次到5次之后土体的抗拉强度趋于稳定。以上对于冻土的拉剪强度特性研究均只局限于试验方面，对冻土在拉剪强度理论方面的研究还很不充分。

关于抗拉抗剪联合公式，已经有大量学者进行了研究与改进，1921年Griffith针对Mohr-Coulomb理论仅适用于压剪区的局限性进行了扩展，将抗拉强度破坏包线与莫尔强度包线合并在一个坐标系下提出利用抛物线拟合拉剪强度包线的方法，在所建立的强度线当中压剪区利用莫尔强度包线表示，抗拉区则利用抛物线表示。之后国内的戴自航等［10］将莫尔-库伦的负半轴包络线作为土体的抗拉强度。实际上后来有学者研究发现由于负半轴的高度非线性，直接将负半轴包络线作为抗拉强度是严重高估了非饱和土的抗拉强度［11］。再后来李广信［12］提出用双曲线对抗拉抗剪强度曲线进行拟合的方法，李荣建等［13］在该方法的基础上分别对拉伸、拉剪、压剪三个破坏区进行应力修正。宋炎勋等［14］对该方法建立的结构性土体双曲线强度进行修正并克服了在Mohr-Coulomb强度理论中夸大土体抗拉强度的问题。郑文等［15］提出了将双曲线强度包线通过变换坐标系，使莫尔圆变成直线来绘制拉剪强度包线，结果具有较高的拟合效果。尽管如此，探究适用于高吸力范围下且考虑冻融循环影响的非饱和土抗拉抗剪联合公式还未有研究。

基于此，本文以位于冀北山区延崇（延庆—崇礼）高速路的路基边坡土为研究对象，利用冻融交变箱来施加不同冻融循环次数，采用蒸汽平衡法来控制高基质吸力。从试验出发首先探究经冻融作用之后高吸力非饱和土体的强度变化规律，绘制经历冻融循环作用之后土体处于高吸力状态下的莫尔圆，将得到的莫尔强度包线结合前人对于抗拉剪强度联合公式的研究成果，应用到受冻融作用后高吸力非饱和土拉剪强度特性研究上，在抗拉区对公式进行验证并与试验值进行比较，最后通过修正使其可以适用于经历不同冻融循环作用后高吸力非饱和土强度曲线的绘制，为北方寒旱交替地区路基边坡土的稳定性分析提供理论依据。

1 试验方案

1.1 基本物理指标

试验土样取自张家口延崇高速路基施工场地的粉质黏土，按照《公路土工试验规程》［16］、《土工试验方法标准》［17］的要求对土样进行了颗粒分析、液限塑限试验和击实试验得到其物理性质如表1所示。

表1 土样的物理性质Table 1 Physical properties of the soil specimens

1.2 试验流程

试验试件采用底面直径39.1 mm，高80 mm的常规三轴试件。试验试件按90%压实度和最佳含水率13%设计，分5层击实成型，脱模后用保鲜膜包裹以防止水分流失。将用保鲜膜包裹好的试件移入高低温交变箱，设定冻融循环次数为0、1、3、5、9次，负温设定为-15℃，冻结时间为12 h，融化时间为12 h，24 h为一次冻融循环。将达到冻融次数要求的试件从冻融交变箱中取出，去除保鲜膜后用游标卡尺测量各个试件的尺寸变化，将试件放入烘箱并设定温度为100～105℃，烘干时间为12 h。将烘干的试件取出，放置在干燥室内待土体温度恢复至室温，最后将抗压试件、抗拉试件与三轴试件置于过饱和盐溶液上方进行蒸汽平衡（图1）。每周称一次质量，当每单个试件的质量变化在一周之内小于0.01 g时认为土体孔隙水压力与对应盐溶液的蒸汽压力达到热力学平衡，则认为此时土体达到对应的吸力值。根据要求平均每个试件在15 s［18］内完成称量。吸力平衡过程中需保证干燥器内环境温度为（20±0.5）℃。三轴抗拉试件则采用底面直径39.1 mm，高16 mm的试件，抗拉试件的吸力平衡过程与抗剪试验一致。本文不考虑渗透吸力的影响，则认为试验所达到的吸力均为基质吸力。

图1 吸力平衡过程Fig.1 The suction equilibrium process

根据全国物理化学计量技术委员会所给出饱和盐溶液对应的标准相对湿度值［19］和Kelvin公式，本试验所采用饱和盐溶液的相对湿度值（RH）及其所对应的吸力值如表2所示，试验中配制的盐溶液为过饱和状态。

表2 饱和盐溶液及其对应的吸力值（20℃）Table 2 Saturated salt solutions and corresponding suction values（20℃）

1.3 抗剪抗拉试验

轴平移法适用于将吸力的范围控制在0～1.5 MPa［20］，对于高吸力的施加则不再适用。利用蒸汽平衡法施加高吸力，将达到吸力平衡的试件迅速测量其体积和质量并移到GDS非饱和土三轴试验仪，试验采用UU试验，陶土板不需要饱和，试验过程中陶土板与试样之间用硬塑料薄膜隔开，防止试样在试验过程中吸水或排水。采用三种低围压40 kPa、60 kPa、80 kPa进行试验，每组围压3个平行试件，数据结果取平均值，试验数据实现自动采集。另取一组试件进行无侧限抗压试验。

抗拉试验采用无侧限直接拉伸仪器，试件两头采用强力胶固定，采用底面直径都是39.1 mm，高度分别取为h=80 mm、h=32 mm和h=16 mm三种尺寸的试件进行拉伸试验，抗拉的过程中为了防止水分散失，将试件周围用油面纸筒包裹，原因是高吸力非饱和土暴露在空气中水分容易散失导致吸力不准，试样破坏效果如图2所示。其中图2（a）所示的是高为80 mm试件的破坏效果，图2（b）所示的是高为32 mm试件的破坏效果。经观察发现破坏位置基本上也在刮毛处附近，并不能反映真实抗拉数据的大小。图2（c）所示的是高为16 mm试件的破坏效果。经过多次试验对比分析得出，高度为16 mm试件的破坏数据最为稳定。

图2 试件破坏效果Fig.2 The effect of specimen destruction

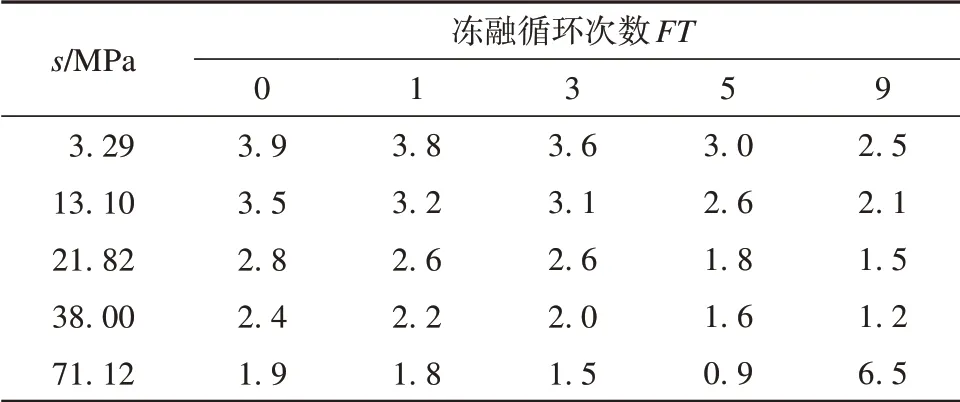
表4 冻融循环后单轴拉伸试验试件的初始含水率（单位：%）Table 4 Initial moisture content of uniaxial tensile test specimens after freeze-thaw cycles（unit：%）

试件经过冻融与吸力平衡后三轴压缩试件与抗拉试件（h=16 mm）的含水率，如表3～4所示。表中每个数据都是由三个平行试件的平均值得到。相比较两种试验方式的含水率，前两位有效数字基本变化不大，但因吸力平衡的判定标准为每周称量试件的质量变化之差小于0.01 g，所以两个表格中含水率的变化在前两位有效数字之后会稍有不同。由于两种试验试件含水率数据很接近，本文只取了三轴压缩试验的含水率，来表现经不同冻融循环作用后达到吸力平衡标准的含水率来绘制土-水特征曲线。

表3 冻融循环后三轴压缩试验试件的初始含水率（单位：%）Table 3 Initial moisture content of triaxial compression test specimens after freeze-thaw cycles（unit：%）

2 土-水特征曲线

采用蒸汽平衡法对不同冻融循环下的试件进行吸力平衡，得出不同冻融循环次数下高基质吸力非饱和土的土-水特征曲线，如图3所示。通过观察得出含水率与吸力是一一对应的关系，且吸力越高含水率越低，同吸力条件下随冻融循环次数的增加含水率逐渐降低。常用的非饱和土的土-水特征曲线模型有BC模型、VG模型、Gardner模型和FX模型。根据前人的经验得出粉质黏土适用模型为Gardner模型［21］，其表达式为

图3 不同冻融循环次数下高基质吸力非饱和土的土-水特征曲线Fig.3 Soil-water characteristic curve of unsaturated soil with high matrix suction under different freeze-thaw cycles

式中：θω为基质吸力下对应的含水率；θr为残余含水率；θs为饱和含水率；s为基质吸力；a、q为模型拟合参数。这里将θs值统一取0次冻融循环条件下的各含水率值，验证Gardner对土-水特征曲线的高吸力部分数据拟合度是否可靠，拟合参数关系见表5。通过表中的确定系数R2可以看出拟合度均不小于90%，说明Gardner对非饱和路基粉质黏土的拟合效果很好。

表5 非饱和土持水特性试验的拟合参数Table 5 Fitting parameters for water-holding test of unsaturated soil

3 寒区边坡非饱和土强度分析

3.1 高基质吸力非饱和土的抗拉抗剪强度

利用抗拉、抗剪与抗压数据绘制出莫尔圆，这里为了节省篇幅，选取FT=0次（未进行冻融循环）条件下不同基质吸力的莫尔圆变化关系曲线，并根据几何关系绘制出非饱和土的莫尔强度包线，如图4所示。

图4 不同吸力下的拉剪莫尔圆Fig.4 Tensile-shear Mohr’s circles under different suctions

取围压为40 kPa时高基质吸力非饱和土的抗剪强度和单轴抗拉强度与吸力的关系绘制双Y轴曲线，如图5（a）所示。本试验吸力范围为3.29 MPa到71.12 MPa，不难发现此时抗剪强度随着吸力升高逐渐升高，抗拉强度则是随着吸力的升高而逐渐降低，间接说明土体孔隙中水分的升高有助于增强其抗拉强度。当吸力值在较低吸力范围下时，由文献［22］得出抗拉强度随含水率的升高呈现先升高后降低的变化趋势。在本文研究的高吸力范围内，非饱和土的抗剪强度与抗拉强度随吸力的变化展现相反的规律。图5（b）所示在FT=0次不同围压下的抗剪强度随吸力的变化关系图，即随着吸力的增加不同围压下抗剪强度逐渐增加。

图5 抗剪强度与抗拉强度随吸力的变化Fig.5 Variation of shear strength and tensile strength with suction

3.2 冻融对抗拉抗剪强度的影响

为了节省篇幅，选取s=71.12 MPa时不同冻融循环条件下莫尔圆的变化关系曲线，莫尔强度包线是利用几何关系将无侧限抗压莫尔圆以及围压分别为40 kPa、60 kPa、80 kPa下莫尔圆进行整理计算得出的，如图6所示。τ坐标轴的左侧为单轴抗拉莫尔圆。

图6 不同冻融循环次数下的拉剪莫尔圆（s=71.12 MPa）Fig.6 Tensile-shear Mohr’s circles under different freeze-thaw cycles（s=71.12 MPa）

取围压为40 kPa时三种吸力（s=3.29 MPa、s=21.82 MPa、s=71.12 MPa）非饱和土的抗剪强度、单轴抗拉强度，绘制其随冻融循环次数变化的关系曲线，如图7中（a）、（b）、（c）所示。可以看出抗剪强度随冻融循环次数的增加而降低，同样抗拉强度也随冻融循环次数的增加而降低。将不同冻融循环条件下的试件利用游标卡尺测量其体积，放入烘箱之后烘干，之后称量其质量，经计算孔隙率数值见表6。结合图7所反映的抗拉抗剪强度均在经历三次冻融循环之后变化趋于稳定，说明抗拉抗剪强度的变化与孔隙率变化存在一定关系。图7（d）为吸力为3.29 MPa时不同围压下抗剪强度与冻融循环次数的变化关系图，由于各吸力在不同围压条件下抗剪强度变化规律一致仅展示其中s=3.29 MPa作为例子，由图可知不同围压下抗剪强度随着冻融循环次数的增加呈逐渐降低的变化趋势。

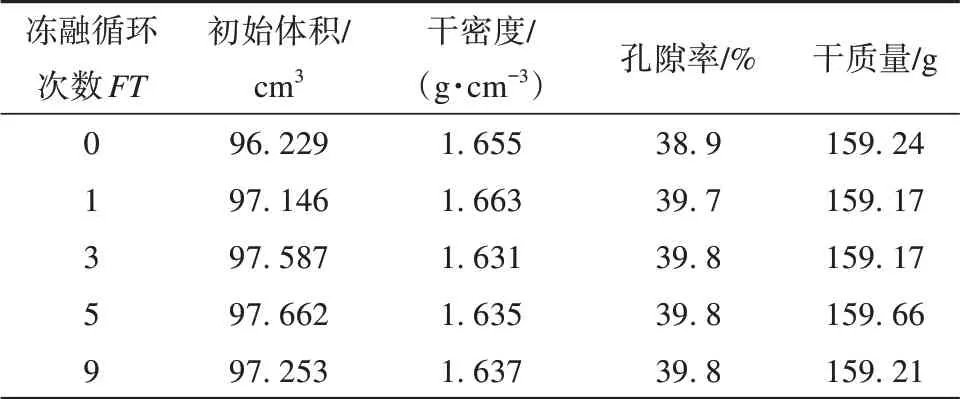
表6 冻融循环后土样的基本物理指标Table 6 Basic physical indicators of soil specimens after freeze-thaw cycles

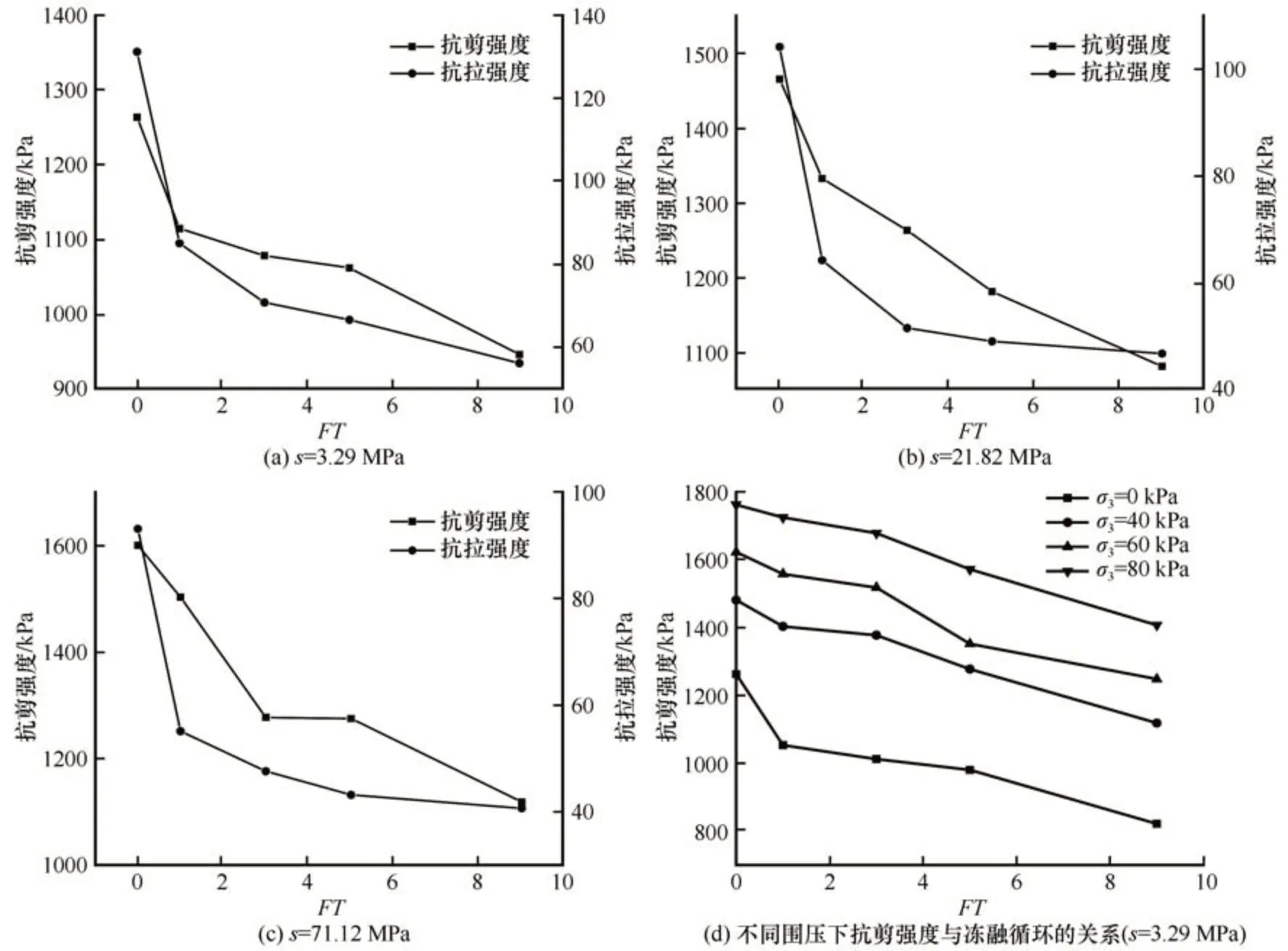
图7 抗剪强度与抗拉强度随冻融循环次数的变化Fig.7 Variation of shear strength and tensile strength with freeze-thaw cycles

4 冻融对高基质吸力非饱和土的影响

4.1 公式值与试验值对比

为分析高基质吸力非饱和土抗拉抗剪强度特性，李广信［12］、郑文等［15］通过开展单轴拉伸试验、单轴压缩试验以及三轴剪切试验，提出抗拉抗剪联合公式为

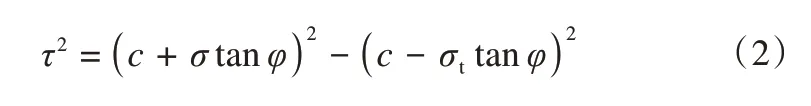
式中：τ为抗剪强度；σ为剪切面上的法向应力；c为土体黏聚力；φ为土体内摩擦角；σt为土体抗拉强度。已知各围压下的抗剪强度利用式（2）来计算得出单轴抗拉强度。比较计算出的结果与试验得到的结果，并分析高基质吸力非饱和土是否适用于该公式。通过式（2）计算得出的抗拉莫尔圆明显大于实际抗拉试验下得出的抗拉莫尔圆见图8（a）。利用公式计算的抗拉莫尔圆与莫尔强度包线延长线基本相切，按照以往的经验总结抗拉区的抗拉破坏包线为非线性，抗拉抗剪联合破坏包线以莫尔强度包线与单轴抗拉莫尔圆的切点为分界，切点右边部分采用莫尔强度包线，切点左边以抗拉莫尔圆的扇形边界为抗拉抗剪联合破坏包线。这种方式为Vesga破坏包线的确定方法［23］，然而作者强调该理论适用于EES稳定区，对于其他吸力范围下的非饱和土如高基质吸力、近饱和状态下的低吸力，并没有说明其具备适用性。

本文以经历9次冻融吸力值为71.12 MPa的拉剪莫尔圆为例，通过试验数据进行进一步分析，将坐标由σ-τ应力坐标换成，其中将图8（a）中σ-τ坐标改为坐标如图8（b）所示，图中OA线由无侧限抗压强度莫尔圆转换而来，线段BB′、CC′、DD′分别由围压为40 kPa、60 kPa、80 kPa下对应的抗剪莫尔圆所转化，将点A、点B、点C、点D进行线性拟合得出一条y=ax+b的直线方程，且拟合度高达99%，得出参数a和b。分别令x=0，y=0得出点T和点V，连接点V和点D得到线段VD作为抗剪强度线Kf。OS和OS′分别为利用式（2）得出的抗拉强度公式值和通过试验得到的抗拉强度实际值，且图中的几何关系为OA垂直于OS和OS′，并通过试验发现OS和OS′共线且与σˉ轴成45°轴上的负值部分实际意义是三向受拉时的应力状态。如图8（c）所示，试验得到的单轴抗拉强度值明显比运用式（2）计算得到的单轴抗拉强度要小很多，即OS＞OS′。按照以往的经验［15］负轴上对应的三向抗拉强度小于或等于单轴抗拉强度。以OS为半径，原点为圆心画圆弧交于负轴点R，通过点R、点S、点A、点B、点C和点D进行非线性拟合，则该曲线可作为利用原始公式计算得到的破坏包线（公式值）。同样方法单轴抗拉强度的实际值对应点P、点S′、点A、点B、点C和点D进行拟合作为破坏包线（实际值），从图8（c）可以观察出以往运用公式得到的破坏包线基本不适用于冻融循环条件下高基质吸力非饱和土的抗拉抗剪破坏包线。

图8 非饱和土的破坏莫尔圆与应力路径及强度破坏主应力线（s=71.12 MPa，FT=9次）Fig.8 Failure Mohr’s circle，stress path and strength failure principal stress line of unsaturated soil（s=71.12 MPa，FT=9）

结合文献［24］中提出采用分段线性峰值应力圆包络线的画法来对公式值与试验得到的单轴抗拉强度实际值的准确性进行比较，对未冻融作用下吸力值为3.29 MPa拉剪莫尔圆经行对比，通过建立线1和线2的方式对高基质吸力非饱和土拉剪莫尔圆进行分析。线1是单轴抗拉强度莫尔圆与无侧限抗压强度莫尔圆的公切线，线2是莫尔强度包线。公式计算结果如图9（a）所示，通过公式计算的单轴抗拉莫尔圆与无侧限抗压莫尔圆的公切线线1与莫尔强度包线线2倾角基本一致，即线1和线2完全可以合成一条线进行分析。实际试验结果如图9（b）所示，在高基质吸力情况下线1与线2并不是一条直线：两条线黏聚力c为线2大于线1，而内摩擦角φ为线1大于线2。

图9 分段线性峰值应力圆包络线（s=3.29 MPa，FT=0次）Fig.9 Stress circle envelope for segmented linear peaks（s=3.29 MPa，FT=0）

4.2 拉剪强度包线联合修正

通过结合并整理多组试验数据拟合，这里引入一个“界值”，在4.1节中已说明抗剪强度线Kf的做法，只需要在σˉ-τˉ坐标系中通过三轴剪切试验数据计算得出线段VD作为抗剪强度线Kf，然后在σˉ-τˉ坐标系下从原点（0，0）出发做y=-x的函数与抗剪强度线Kf相交，原点（0，0）与交点之间的距离定义为“界值”，并以此来衡量公式计算抗拉值和实际抗拉值以及界值的大小关系。以表7（FT=0次）和表8（s=71.12 MPa）为例，以图10（a）中的OS和OS′两条线段的长度来代表单轴抗拉强度值，分别观察吸力和冻融循环对强度的影响。

其中表7是未经冻融循环作用下各吸力下单轴抗拉强度的实际值OS′、公式值OS以及界值之间的关系，如表所示公式值与实际值均随吸力的升高逐渐降低，说明在高基质吸力下非饱和土的抗拉强度随着吸力的升高而逐渐降低。表8为吸力为71.12 MPa经不同冻融循环下抗拉强度的公式值与实际值之间的关系对比，发现随着冻融循环次数的增加公式值与实际值均降低。三次冻融循环之后单轴抗拉强度随冻融循环次数的增加而降低的幅度逐渐减缓，进一步说明式（2）不能准确计算在冻融循环作用后高基质吸力非饱和土的抗拉强度值。通过两组试验，表7～8可以发现存在关系：公式值OS≥界值＞实际值OS′。依照此关系对经典联合公式进行修正。

表7 不同吸力下单轴抗拉强度的实际值OS′、公式值OS与界值（FT=0次）Table 7 Actual value OS′，formula value OS and boundary value of uniaxial tensile strength under different suctions（FT=0）

表8 不同冻融循环次数下单轴抗拉强度的实际值OS′、公式值OS与界值（s=71.12 MPa）Table 8 Actual value OS′，formula value OS and boundary value of uniaxial tensile strength under different freeze-thaw cycles（s=71.12 MPa）

公式值由双曲线公式拟合进行轴平移得来。

式中：a为图8（a）中双曲线实半轴长；b为图8（a）中双曲线虚半轴长。

将该双曲线公式进行轴平移，平移的效果为两个坐标系纵坐标数值不变，σ0-τ0坐标系的横坐标向右平移ccotφ得到σ′-τ′坐标系，该坐标与原始坐标系σ0-τ0的关系为

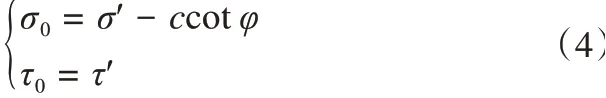
考虑σ0-τ0坐标系得到双曲线与横坐标轴的交点为（ccotφ-σt，0），将该点代入式（3）得到

库伦包线则可以视为是双曲线的一条渐近线，其表达结果为

将式（6）代入式（5），并将a替换得到

将以上的式（7）和式（5）分别代入式（3），并将a和b替换得到

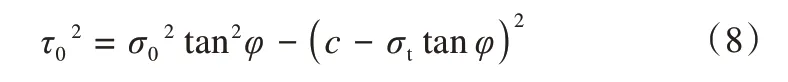
将式（4）代入式（8）就可以得到经典联合公式（2）。根据之前的分析，该公式并不适用于高基质吸力下非饱和土的抗拉强度，其实际值比公式值明显偏小。

通过将本文的试验数据如表7～8所示，并在图8（b）中用σˉ-τˉ坐标系表示。假设在三向受拉下极限强度为单轴抗拉强度，则利用相同的方法得到

式中：β为坐标系下抗剪强度线Kf的倾角；g为坐标系下破坏包线与τ轴的交点。其关系位置可见图10。由于高基质吸力条件下公式值普遍低于界值，这里令界值为w，OS′为σt′，则定义参数a1为σt′/w，则抗拉区的比例公式为

图10 几何分析简单说明Fig.10 A simple illustration of geometric analysis

由以上几何关系可知，在高基质吸力条件下公式值与抗剪强度线Kf基本相交。通过计算可以得出

将式（10）和式（11）代入式（9），得到

由于角β与内摩擦角φ的几何关系为

将式（13）代入式（12）可得

通过式（14）对表8中的FT=1次和FT=9次的情况进行验证，结果如图11所示，式（14）的计算结果与试验值较为贴近。因此以式（1）为基础提出式（14），适用于高基质吸力在冻融条件下土体的拉剪破坏准则。该公式应用领域主要是针对经历寒旱交替综合作用的土体。冻融循环作用改变土体内部孔隙结构，高吸力则是模拟土体在经受冻融作用之后进入的干旱状态。

图11 抗拉区修正公式的验证效果Fig.11 Verification effect of correction formula for tensile zone

5 结论

（1）利用蒸汽平衡法得到高基质吸力条件下的土-水特征曲线，发现含水率随吸力的升高逐渐降低，随着冻融循环次数的增加土-水特征曲线逐渐下移。利用Gardner模型对土-水特征曲线进行拟合发现效果比较合适，说明粉质黏土在高基质吸力条件下，该模型同样适用。

（2）通过抗拉抗剪莫尔圆对比，发现高基质吸力下抗拉莫尔圆与抗剪莫尔圆相差很大，且抗剪强度随着吸力的增加逐渐增大，抗拉强度随吸力的增加而降低。随冻融循环次数的增加抗拉、抗剪强度均逐渐降低，且都反映出在第三次冻融循环之后强度的下降幅度有所减缓，其原因是三次冻融循环之后孔隙率趋于稳定，间接说明高基质吸力条件下，强度的大小主要与土的骨架结构有关。

（3）通过本文的研究分析得出以往的抗拉抗剪联合公式不适用寒区非饱和土强度计算，尤其当吸力变大时前人的抗拉抗剪强度联合公式所得出的结果要大于实际结果很多。基于此通过几何关系引入“界值”概念，利用σˉ-τˉ坐标系与σ-τ坐标系建立联系，进而将初始拉剪联合公式修改为适用于高基质吸力、不同冻融条件的抗拉抗剪联合公式。经验证采用本文提出的方法计算得到的计算值与试验值更为接近，因此本文提出的破坏准更适用于寒区非饱和土强度计算，为今后的寒旱区路基边坡土体更精确的稳定性分析提供计算依据。