探究构图 优化路径 提升素养
——记一道解析几何题的求解历程
2022-11-16江苏省石庄高级中学226531
石 鹏 (江苏省石庄高级中学 226531)
解析几何的基本思想是用代数方法研究平面图形问题,平面图形是由点、线所构成,简称为“构图”.教师教学过程中应带领学生充分探究“构图”中各元素之间的关系,挖掘构图的几何特征和性质,寻找最优运算路径,简化运算过程,提升运算素养.本文以一道模考题的讲评为例,带领学生通过对构图的探究,产生不同的运算路径,比较各个运算路径的优劣,在探究和比较中培养学生的运算素养.
1 问题呈现
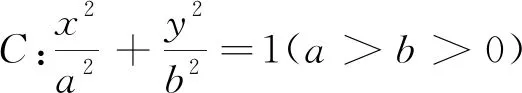

图1
(1)求椭圆C的标准方程;
(2)过T(t,0)(t>a)作斜率为k(k<0)的直线l交椭圆C于M,N两点(点M在点N的左侧),且F1M∥F2N,设直线AM,BN的斜率分别为k1,k2,求k1·k2的值.

2 根据题意,释学生之惑
2.1 设而不求 整体代换
由于点M,N是直线l与椭圆C相交而得到,将直线l的方程与椭圆C的方程联立,借助韦达定理,进行整体代换求解.




2.2 巧用性质 简化运算
学生卡壳的问题得以解决,脸上露出了欣喜的笑容,但同时也需要进行反思:在练习和考试的过程中,遇到类似问题,要心平气和地、理智地进行分析,充分挖掘题目的隐含条件,要敢于去探索,善于解决问题,克服各种“隐形”的困难.此时有学生提出了另一种想法.


2.3 借助中点 寻求斜率
解法1,2是将直线的方程和椭圆的方程进行联立,运算过程比较繁琐,教师引导学生思考:不联立方程,又能否解出来呢?请学生思考后再小组讨论,试探究直线F1M的斜率与直线l斜率间的关系.学生思考片刻后开始讨论,然后有一个学生主动板演出如下解题过程.


评注以上三种解法的运算过程都比较繁琐,解法1和解法2都需要把直线l和椭圆联立,解法1需借助“韦达定理”或者分别求出x1,x2,这对学生的运算和思维要求都比较高.解法2借助椭圆的结论简化了运算,这需要学生在平时学习过程中注意对圆锥曲线中的“亚结论”进行归纳和总结,以便在解题过程中达到游刃有余的境界.解法3利用了点差法,或者通过解法1的①式求出M,N中点Q的坐标,写出直线OQ的斜率,探究出直线MF1,NF2的斜率与直线l的斜率.表面上没有把直线方程与椭圆方程联立,运算量会小一点,实际上把点M或者点N的坐标代入椭圆寻找k与t的关系,涉及到4次,这对学生运算能力的要求也比较高.
3 简化构图 优化路径


图2
3.1 知点解点 建立等式
该生提供了自己的方法:联立直线AM与椭圆C的方程,用k1表示点M的坐标,同理用k2表示点N的坐标,借助于F1M∥F2N建立k1和k2的等式关系进行求解.这就是常见的知点解点模型.

3.2 利用平行 直接求解
也有其他学生发现,由直线F1M与直线F2N平行知斜率相等,设一个变量将运算进行到底.关键是如何设直线方程,将直线F1M设为x=my-1,还是设为y=k(x+1)呢?学生小组讨论发现,如果把直线F1M和椭圆联立,不管是解出横坐标还是纵坐标,都是两个解.旋转F1M可知,横坐标有可能两个都是负的或者一正一负,而纵坐标只可能一正一负,所以解纵坐标比较方便,从而需消去参数x,并且直线经过的定点在x轴上,所以直线方程设为x=my-1比较合理.

3.3 联立直线 代入椭圆
此时有学生指出,以上两个方法的运算量都有点大,可类比解法3,把两条直线的方程联立解出点M,N后代入椭圆,消去斜率k,即寻找到k1,k2之间的关系.

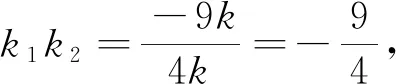
4 重新构图 凸显本质
椭圆作为几何图形,具有对称性、有界性等性质.在解析几何题目的运算过程中,借助于相关性质,可以大大地简化运算,如本题可以引导学生借助椭圆对称性来简化运算.
解如图3,延长MF1交椭圆于点H,由直线F1M∥F2N,点F1,F2和椭圆C关于原点对称,得点N,H关于原点对称,所以直线AH的斜率等于k2.设点M(x1,y1),H(x2,y2),直线MH的方程为x=my-1.

图3

评注借助对称性让题目回归到常见的模型,避免了复杂冗长的运算.平时教学要引导学生储备好相关平面几何的知识和圆锥曲线中必要的“亚结论”,比如:三角形中的三线及三角形面积的求法,与圆相关的垂径定理、切线长定理、相交弦定理等,圆锥曲线中的极点和极线的关系、焦点三角形等,同时培养学生能够充分挖掘图形各元素间的关系,把这些关系转化为代数关系,利用数形结合的思想方法,将复杂的代数运算转化为几何问题.
5 结束语
解析几何问题归根结底还是几何问题,在解决相关问题的时候,不能一味强调代数运算,而应该综合考虑构图中不同元素间的关系,通过探究构图、简化构图、重新构图,让问题回归到常规,让运算回归常见,学生就能够有的放矢,就能将运算进行到底.最重要的是通过探究构图,学生更容易挖掘出几何背景,以便充分利用图形的特征,以形助数,优化运算的路径,调整运算的步骤,减少复杂的运算,提高运算的效率和准确率,最终提升运算素养.
