基于组合赋权逼近理想解排序法-物元可拓模型的农业园区综合能源系统评价

2022-11-16程江洲冯梦婷李欣冯馨以闫冉阳张晓瑀

科学技术与工程 2022年29期

程江洲，冯梦婷，李欣，冯馨以，闫冉阳，张晓瑀

(1.三峡大学湖北省微电网工程技术研究中心，宜昌 443002； 2. 三峡大学电气与新能源学院，宜昌 443002)

2020年，《中共中央国务院关于抓好“三农”领域重点工作确保如期实现全面小康的意见》指出，要有效扩大农业农村投资，启动实施现代农业设施投资项目[1]，同时可实现农业“碳中和”，有助于国家实现“碳达峰”的目标[2]。建立农业园区综合能源系统是农业园区发展的关键，它既推动了设施农业的发展，同时也会带来安全问题[3]，为了分析其建设和运行水平的优劣，需要对系统进行全面综合评价。

目前中外学者已从不同的角度对综合能源系统做了大量研究。任洪波等[4]以校园为例，建立了综合能源系统的规划模型，基于Nash均衡定理，实现系统效益最大化。施泉生等[5]考虑了冷-热-电设备，构建了区域综合能源系统模型，利用改进的模拟退火-粒子群算法对模型求解，减少了系统运行成本。Siddiqui 等[6]设计了一种氨储能的综合能源系统模型，并进行动态模拟与分析，提升了综合能源系统的运行效益。上述综合能源系统研究应用场景多为学校、工业园区，而农业园区综合能源系统的研究还处于起步阶段。文献[7]提出了一种计及风光就地消纳的设施农业园区综合能源系统多目标优化调度方法，考虑多种约束条件，有效降低园区日运行费用、提高风光就地消纳率。文献[8]构建了农村多能流微能网模型，并采用改进杂交粒子群算法实现其经济优化调度。现有的农业园区综合能源系统研究侧重于模型建立和运行优化，对其系统评价的研究很少。文献[9]对综合能源系统的技术性与经济性指标评估，主要分析可再生能源接入系统的影响。文献[10]从能源、环境和经济3个指标角度出发，基于层次分析法(analytic hierarchy process，AHP)-熵权法与灰色关联法给出了综合能源系统合理配置的建议。文献[11]建立了输配一体化综合能源系统模型，基于经济、转化效率、能源环保等多类指标，采用混合等分散蒙特卡洛抽样法进行快速评估。受限于综合能源的发展历程，现有指标体系多以城市为背景，无法与农业园区综合能源系统特征相匹配，且指标属性较为片面。此外，传统评价模型难以在主、客观性上取得平衡，评价结果不够科学合理。

针对以上问题，现提出一种基于组合赋权优劣解距离法-物元可拓(technique for order preference by similarity to an ideal solution-matter-element extension，TOPSIS-MEE)模型的农业园区综合能源系统评价方法。首先建立典型的农业园区综合能源系统架构，并提出一套完整的评价指标体系，采用最小鉴别信息原理平衡改进的AHP-CRITIC 组合法求出的主、客观权重，其次用物元可拓模型(MEE)优化优劣解距离法(TOPSIS)，最后对评价对象进行等级判定和排序。

1 农业园区综合能源系统架构

农业园区综合能源系统主要分为“源-网-储-荷”4个部分，通过能源的生产、传输、转换、储存和使用，以及能源之间的多向互动支撑，最终实现农业园区综合能源系统高效环保的目标，系统结构如图1所示。

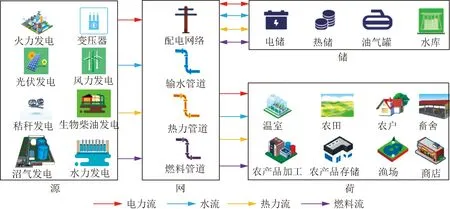
图1 农业园区综合能源系统架构

(1)农业园区综合能源系统——“源”。是指利用光伏、风机、沼气和锅炉等，以可再生能源为主，将其转换为综合能源系统所需要的冷-热-电能量。

(2)农业园区综合能源系统——“网”。是指将“源”产生各种能量通过能源网在系统中传输转换，主要利用电力网、燃料管道和热力管道等设备作为载体，还有一些小型交换机，例如电-热转换装置、电-冷转换装置和冷-热转换装置等。

(3)农业园区综合能源系统——“储”。是指各种能量储存装置，例如大容量蓄电池、冷热气储能罐等，这些装置使可再生能源的就地消纳能力会得到提升，同时也抑制了其出力的波动性，实现了削峰填谷的作用。

(4)农业园区综合能源系统——“荷”。是指系统内部各种能量利用点，主要有冷、热、电3种负荷点。

2 农业园区综合能源系统评估指标

目前对于农业园区没有一套完整的评估指标体系，综合了多数文献中所提到的农业园区评估指标[12-13]，并根据上述农业园区综合能源系统架构图，建立了经济性、技术性和环保性3个一级指标，以及14个二级指标的农业园区综合能源系统评估体系，如图2所示。

图2 农业园区综合能源系统指标评估体系

2.1 经济性指标

物质资源的产出状况是衡量区域经济发达程度的核心指标，农业园区综合能源系统经济性指标包括农业总产值、劳动生产率、资源产出率和单位生产总值能耗。其具体计算公式为

Va=YaC

(1)

Rw=Vp/Np

(2)

Rr=Vp/Minput

(3)

Ec=Einput/Vp

(4)

式中：Va为农业总产值，万元；Ya为农业产品产量，t；C为价格，元/t；Rw为劳动生产率，万元/人；Vp为园区生产总值；Np为园区从业人口；Rr为资源产出率，万元/t；Ec为单位生产总值能耗，tce/万元，tce表示能耗单位；Minput为直接物质投入量；Einput为能源投入量。

2.2 技术性指标

设备运行年限、设备无故障率、设备过载率以及供电、供热、供冷可靠率是衡量综合能源系统运行状态的重要参考指标。

(1)设备运行年限A1。其计算公式为

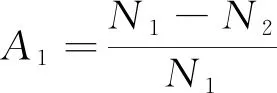
(5)

式(5)中：N1为设备预期使用年限；N2为设备已使用年限。

(2)设备运行无故障率A2。其计算公式为

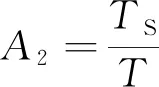
(6)

式(6)中：TS为设备无故障状态运行时间；T为设备运行总时间。

(3)设备过载率A3。其计算公式为

(7)

式(7)中：N1为设备预期使用年限；NG为设备过载年限。

(4)供电可靠率B1。其计算公式为

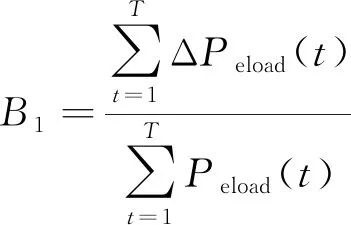
(8)

式(8)中：T为系统运行周期；ΔPeload(t)为系统电能在t时刻的缺供功率；Peload(t)为系统电能负荷在t时刻的需求功率。

(5)供热可靠率B2。其计算公式为

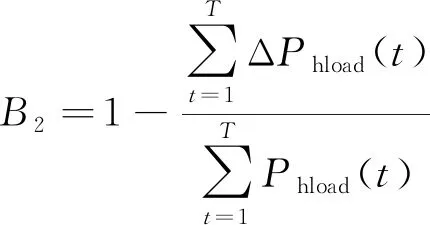
(9)

式(9)中：ΔPhload(t)为系统冷能在t时刻的缺供功率；Phload(t)为系统冷能负荷在t时刻的需求功率。

(6)供冷可靠率B3。其计算公式为

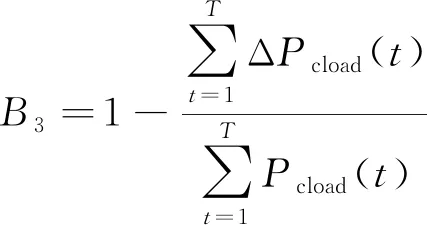
(10)

式(10)中：ΔPcload(t)为系统热能在t时刻的缺供功率；Pcload(t)为系统热能负荷在t时刻的需求功率。

2.3 环保性指标

环保性是当今综合能源系统的发展趋势，除了对经济、技术等方面评价外，还需要对社会、环境等多方面进行评价。

(1)综合能源利用率。该指标表征综合能源系统对多种能源的利用效率水平。其计算公式为

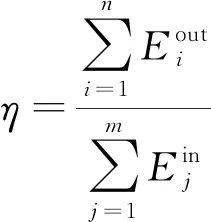
(11)

(2)污染物排放量。在微型燃气轮机和燃气锅炉工作的时候会释放NOx和CO2等对环境有害的气体，其计算公式为

(12)

式(12)中：Cpo为微能网各污染物的总排放量；sk为微能网第k种污染物的排放系数；U为污染物的类型数目。

(3)废旧资源综合利用率。一般情况下，没有资源化利用的废弃物会直接溢散在生态系统中，由于这些废弃物在自然状况下难以大量生成，因此会对生态系统造成不同程度的影响。因此，废弃物排放的多少直接关系区域经济发展能否长远，该指标数据通过实地调查获得。

(4)可再生能源装机占比v。其计算公式为

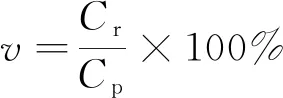
(13)

式(13)中：Cr为新能源装机容量；Cp为总装机量容量。

3 组合赋权TOPSIS-MEE综合评价模型

组合赋权TOPSIS-MEE综合评价模型首先是将改进的AHP法和CRITIC法分别对主、客观性指标赋权，然后采用最小鉴别信息原理得到整体评价模型中各指标综合权重，最后运用TOPSIS-MEE模型对评价对象进行等级判定和排序。

3.1 改进的AHP算法

改进的AHP算法构建判断矩阵时使用3标度法1、0、-1，以比较各层因素。3标度法可以使专家轻松地对2个因素相对重要性做出判断，避免一致性检验步骤所需要的庞大复杂计算，简化计算过程。改进AHP算法步骤如下。

步骤1一级指标采用3标度法( 1, 0, -1 )建立判断矩阵A=(aij)n×n，则

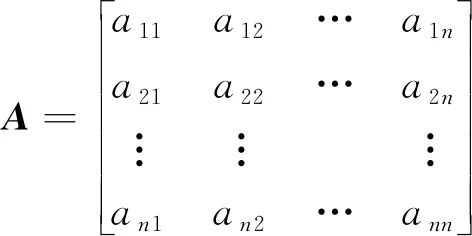
(14)

式(14)中：

(15)

步骤2确定最佳传输矩阵。矩阵A的最佳传输矩阵为O=(oij)n×n，则

(16)

式(16)中：

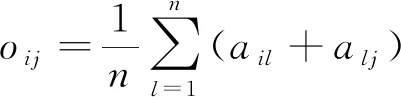
(17)

步骤3确定最佳一致性矩阵。矩阵O最佳一致性矩阵为C=(cij)n×n，则

(18)

式(18)中：

cij=exp(oij)

(19)

步骤4二级指标同样采用上述算法计算。

步骤5权重计算，各个指标的主观权重αi为

(20)

3.2 CRITIC算法

CRITIC算法是一种客观赋权法，根据评价指标之间的对比和冲突情况，进而对指标客观权重综合衡量。同时兼顾指标变异性和相关性，完全利用数据自身的客观属性进行科学评价。其计算步骤如下。

假设有m个样本、n个指标，则评价矩阵可表示为

(21)

步骤1指标无量纲化处理。各指标量纲不同会对评价结果造成影响，所以需要进行无量纲化处理，即

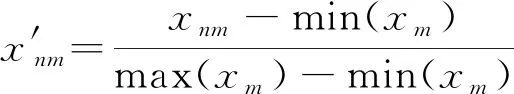
(22)

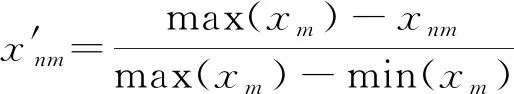
(23)

步骤2确定指标变异性。用标准差表示各指标取值的波动性，若指标数值波动大，则标准差大，说明该指标信息丰富，评价强度高，应被分配更多的权重，即

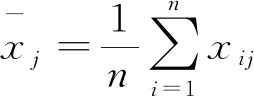
(24)

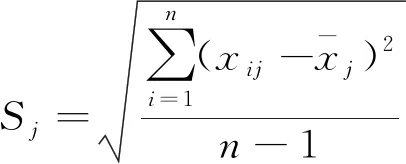
(25)

式中：Sj为第j个指标的标准差。

步骤3确定指标冲突性。用相关系数表示各指标间的相关性，若该指标相关性越大，则其冲突性越小，说明该指标反映越多的相同信息，评价内容存在重复，应减少被分配的权重，即

(26)

式(26)中：rij为评价指标i和j之间的相关系数。

步骤4计算客观权重。

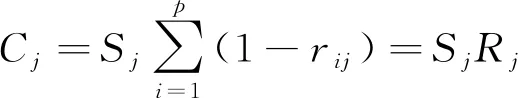
(27)

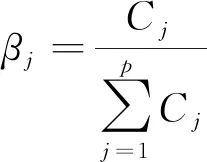
(28)

式中：Cj为第j个评价指标所包含信息量；βj为该指标的客观权重。

3.3 组合方法赋权

上述改进AHP算法得出了主观权重αi与CRITIC算法得出了客观权重βj，由于单一采用主观或客观权重会导致评估结果不精确，为了使综合权重Wi尽可能接近αi与βj，而不偏向其中任意一项，采用了最小鉴别信息原理来求取综合权重Wi，计算公式为

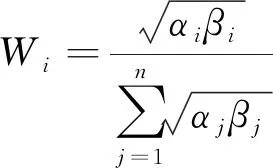
(29)

3.4 TOPSIS-MEE模型评价

TOPSIS法是对评价对象与理想点距离计算后排序的方法。首先分别计算出各评价对象与理想点最优解、理想点最劣解之间的距离，如果评价对象离理想点最优解最近，离理想点最劣解最远，那么该评价对象排序第一。其原理如图3所示，a、b点分别为理想点最优解、理想点最劣解，c、d两点为处于两理想点中垂线上的评价对象，而位于中垂线上的点相对距离都为0.5，无法区分远近，适用性受到限制。

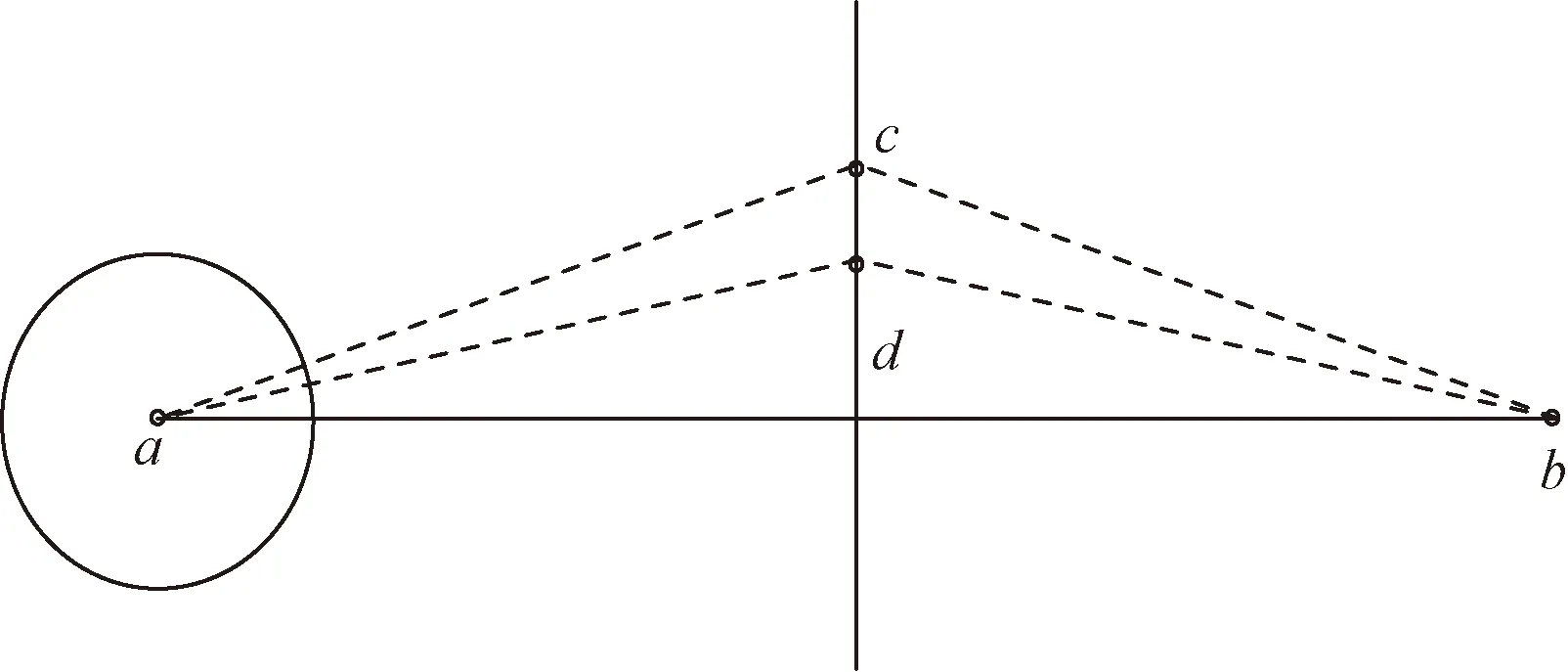
图3 TOPSIS原理图

为改善TOPSIS法中相对距离的缺陷，引入了物元可拓模型来进一步量化评价结果。具体步骤如下。

步骤1构造初始评判矩阵Y。

步骤2构造加权规范矩阵Z。将初始评判矩阵进行归一化处理得到Y′，并通过各指标的综合权重Wi求得加权规范矩阵Z。

(30)

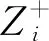
(31)

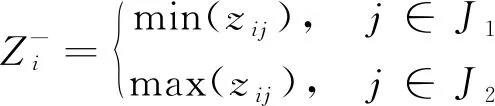
(32)

(33)

(34)

式中：J1为极大型指标；J2为极小型指标。

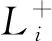
步骤5确定加权规范矩阵Z中相关评价指标和每个区间的贴进度D(Ni)和加权贴进度Kj(Ni)。

(35)

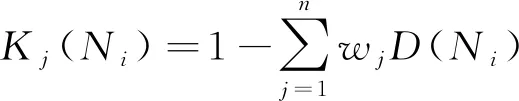
(36)

步骤6计算加权贴近度Kj(Ni)的特征值∂i，利用特征值可进一步对评价对象做出排序，以避免多个评价对象属于同一层次。

(37)

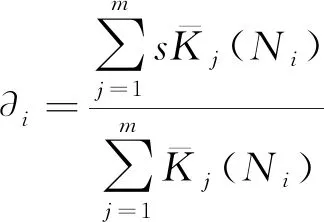
(38)

4 算例分析

选取某农业园区为例验证所提规划指标的合理性与所提方法的优越性，现有3种不同的综合能源规划方案，如表1所示。评价体系中的部分指标，如可再生能源的装机比例等，采用算例所给参数进行直接计算，其余指标基于 MATLAB平台运进行求解，具体数值如表2所示。

表1 规划方案中各装置的功率和能量值

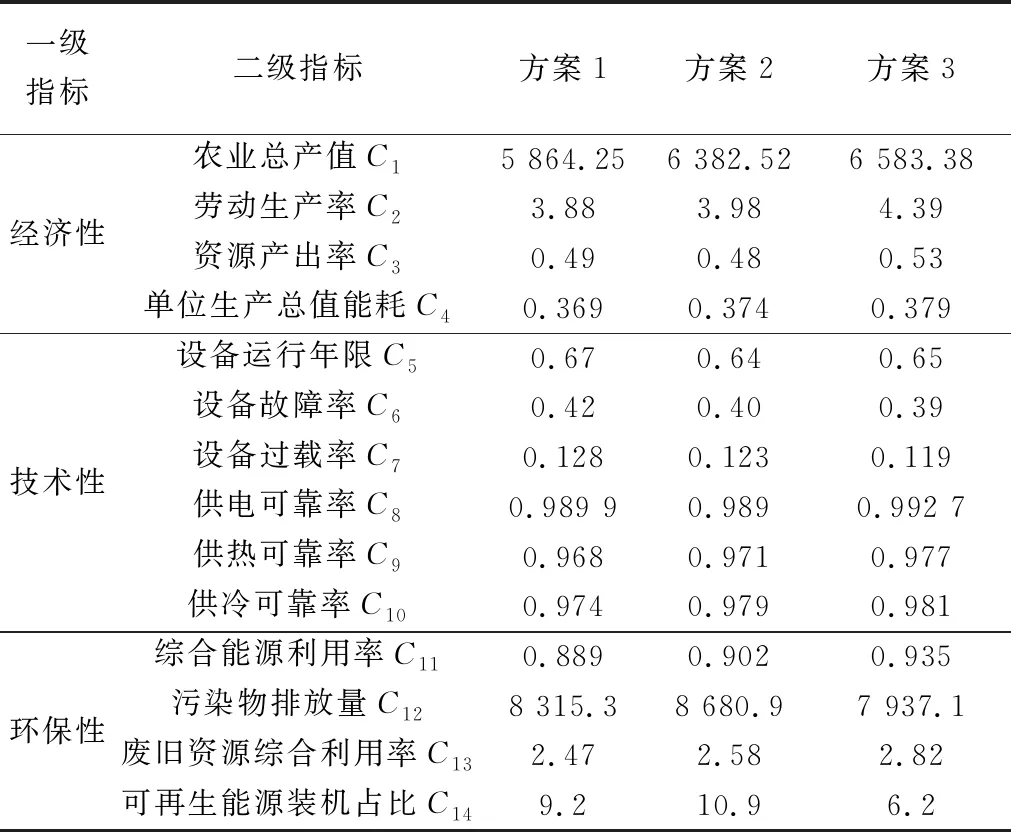
表2 评价体系中各指标数据

4.1 指标权重的计算

4.1.1 基于改进的AHP算法权重

首先使用3标度法构造一级指标的判断矩阵，求得一级指标对目标层的权重，再对二级指标构造判断矩阵求出权重，进而依次相乘即为各二级指标对目标层的权重，如表3所示。

4.1.2 基于CRITIC算法的权重

根据式(21)～式(28)进而确定出各二级指标对目标层的权重，如表4所示。

4.1.3 二级指标的综合权重

将表3中主观权重和表4中客观权重通过式(29)计算得出各个二级指标的综合权重，如表5所示。

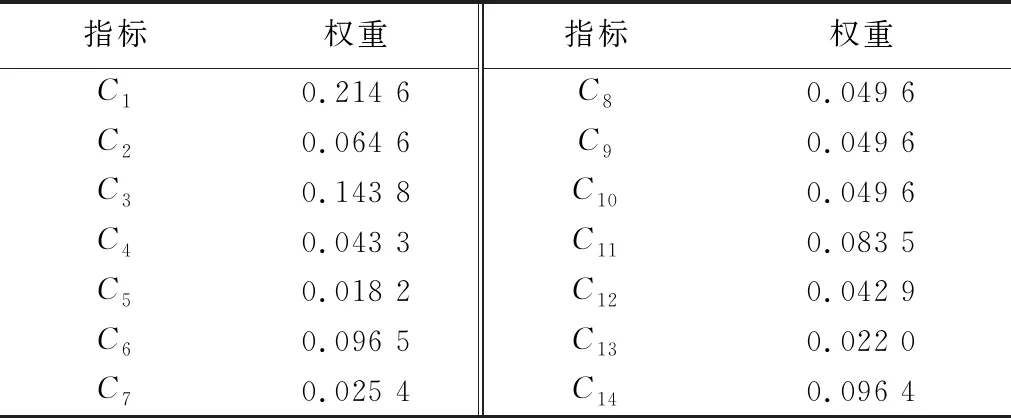
表3 基于改进AHP算法的二级指标权重

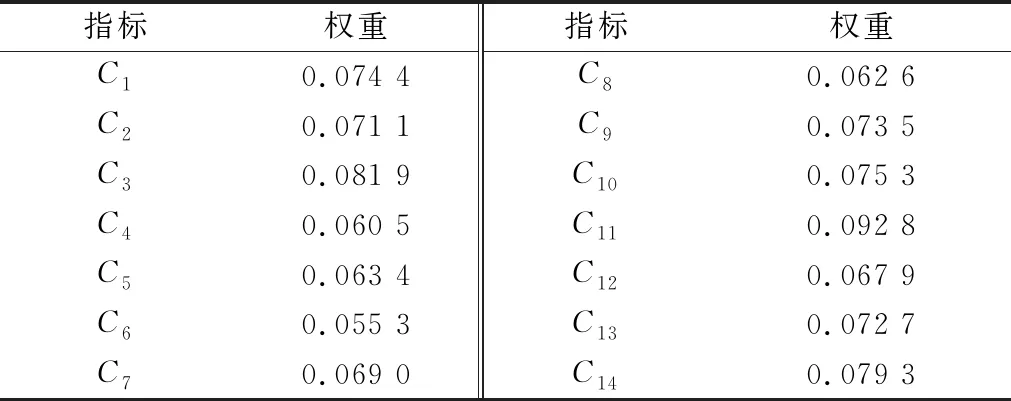
表4 基于CRITIC算法的二级指标权重

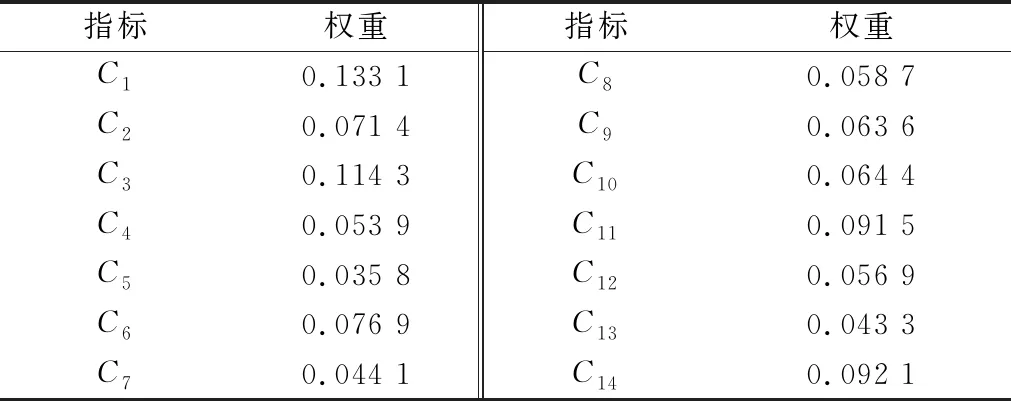
表5 各二级指标的综合权重

图4为3种算法的权重对比图。可以看出，组合算法综合了主客观权重后，其整体趋势与另外两种方法相近，具有一定的可信度。同时经济性与环保性指标会高于传统客观算法所求的权重，符合新时代能源发展对经济环保的要求。因此所提综合权重方法更合理、准确。

图4 3种算法权重对比

4.2 综合评估与分析

首先按构造出初始评判矩阵Y，并通过归一化处理得到Y′和各指标的综合权重Wi求得加权规范矩阵Z，即

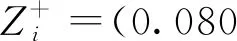
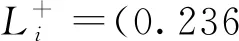
将正负理想距离构成的区间划分成4个等级，即优秀、良好、中等和一般。以指标C1为例，其正理想距离为0.236 0，负理想距离为0.259 5，则区间分为

U11=(0.236 0,0.241 9)；

U12=(0.241 9,0.247 8)；

U13=(0.247 8,0.253 6)；

U14=(0.253 6,0.259 5)。

其他指标也分成等距，计算矩阵Z与4个评级的贴近度。结果如下。

根据各指标的贴近度，分别计算3个方案相对于4个评价等级的加权贴近度，即

K(S1)=[0.993 5 0.996 9 0.997 6 0.992 4]；

K(S2)=[0.994 1 0.997 0 0.997 9 0.995 1]；

K(S3)=[0.993 0 0.994 0 0.997 4 0.998 5]。

图5是每个方案的加权贴近度，3个方案的综合评价分别为良好、良好、优秀。基于TOPSIS模型，方案1和方案2的综合评价水平均为良好，需要进一步计算特征值，实现评价等级的准确划分。因此， TPOSIS模型不能有效应用于综合评价，准确性不够。

图5 3种方案的加权贴进度对比

由特征值公式计算出3个方案的特征值，如表6所示。

由表6可以看出，3个方案的综合评价最终排名为方案3>方案2 >方案1。根据TOPSIS模型，方案1和方案2的综合评价等级相同，无法进一步划分。因此将MEE方法的特征值应用于TOPSIS模型，求出方案2的特征值大于方案1的特征值，因此方案2的综合评价等级高于方案1。与TOPSIS模型相比，MEE优化后的TOPSIS模型能更好地实现数据的科学处理，综合评价结果更加可靠有效。