分布式电源逆变器的功率控制

刘向宁 王忠博 牛威

（国网大连供电公司 辽宁省大连市 116001）

以风能和太阳能为基础的分布式电源（Distibuted Generation, DG）相对成本较低、技术成熟、可靠性较高，近年来发展迅猛[1,2]。与传统的火力发电不同，各种不同类型的DG（光伏风电、风电、电池储能等）可通过电力电子变流器实现并网，并利用逆变器控制实现对有功功率和无功功率的调节，在特殊情况下对逆变器采用无功控制为电网提供电压支撑[3,4]。尤其当GD 高渗透并网时，其逆变器的无功调节能力甚至可以完全取代调压电容器。

大量DG 的接入，增加了大电网整体的控制难度，恶化电网的电能质量（主要指频率和电压），电网的可靠性将会收到影响。为了降低电网对DG 接入的敏感性，由DG、储能装置、控制中心与用电负荷等构成的微电网应运而生[5]。其中对DG 逆变器的有效控制成为关键。

目前，常用的DG 逆变器控制多采用Droop 下垂控制、V/F 控制、PQ 恒功率控制等控制策略。其中，Droop 下垂控制和V/F 控制用于DG 在微电网孤岛运行时使用；并网运行时，DG 逆变器可采用PQ 控制策略[6]。

本文以分布式发电为模型，讨论在并网运行模式下的PQ 控制策略，并在MATLAB/ SIMULINK 环境下对控制效果进行验证。结果表明该控制策略可实现有功和无功的准确跟踪，充分发挥DG 本身有功与无功的调节能力，促进DG的高渗透消纳，发挥DG 的能效和环境效益。

1 PQ恒功率控制原理

1.1 三相并网逆变器拓扑结构

本文所涉及的DG 并网结构如图1 所示。其中，T1～T6为三相逆变器桥的6 个开关管， L 为滤波电感，C 为直流母线电容，R 为包括电抗器电阻在内的每相线路的电阻，usa、usb、usc 为电网电动势。

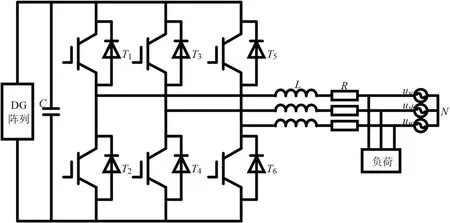
图1：三相并网逆变器拓扑结构图

1.2 PQ控制原理

在PQ 控制策略下，将u 定义为DG 内部逆变器并网时的三相基波电压，则：

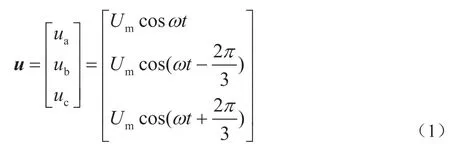
其中，Um为相电压的幅值。

对u 进行dq0 变换，可得其在旋转坐标系下的表达式为[7]：

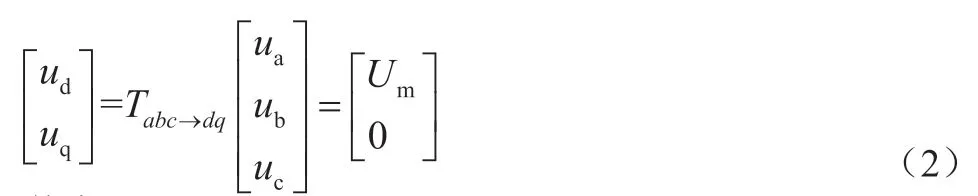
其中，

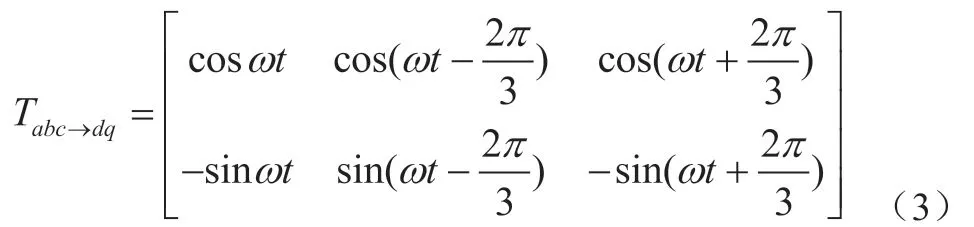
定义，i为逆变器的输出电流，id、iq分别为dq0变换下的d、q 轴电流。根据瞬时功率理论，逆变器输出的瞬时有功功率P 和瞬时无功功率Q 在dq0 旋转坐标系中的表达式为：

假设保持逆变器的输出有功功率为Pref，无功功率为Qref，根据式（2）和式（4），可以得到逆变器的参考电流为：

根据式（5）知，逆变器产生的瞬时有功功率仅与其输出的d 轴分量电流有关，而逆变器产生的瞬时无功功率仅与其输出的q 轴分量电流有关，从而将对逆变器输出功率的控制转化为对电流的控制。如图2 即为PQ 控制策略的原理图。

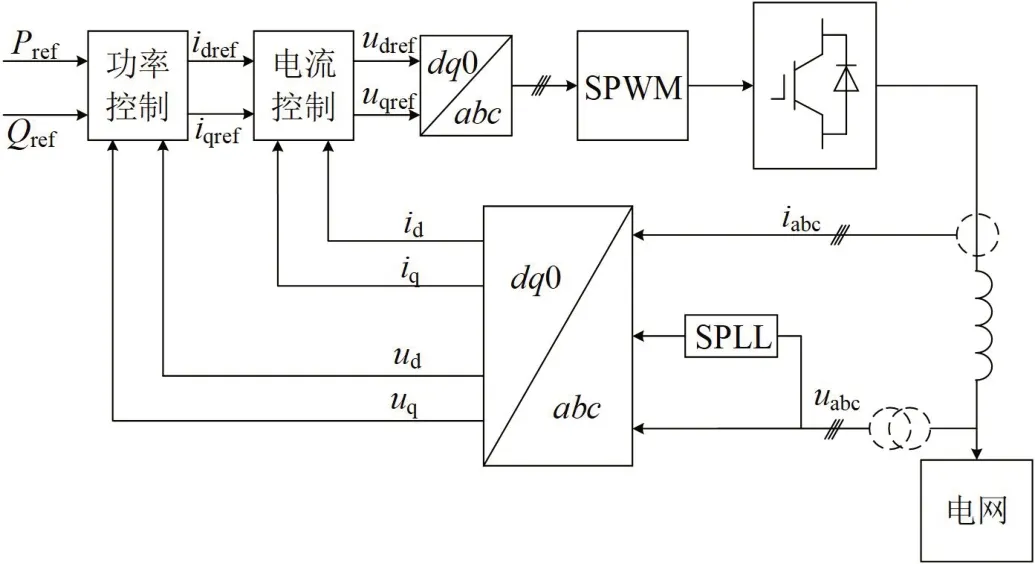
图2：并网逆变器PQ 控制原理

2 PQ恒功率控制模型

图2 所示的PQ 控制由功率外环、电流内环以及SPLL锁相环构成[8]。下面分别进行介绍。

2.1 功率外环控制设计

功率外环控制其作用是使得逆变器的输出为参考基准功率，实现无差控制。为了实现无差控制，外环功率控制的控制器通常采用PI 控制，得到的参考电流表达式为：

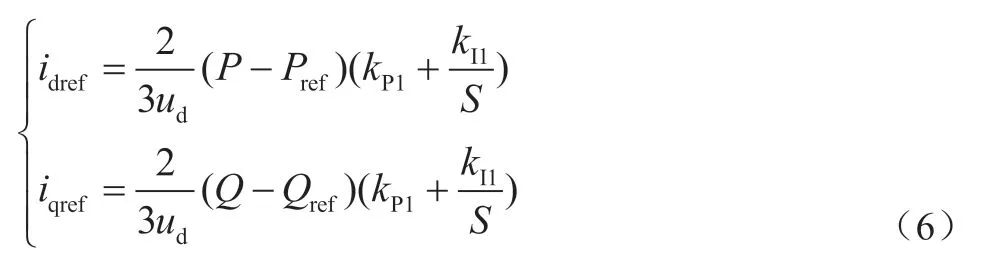
其中，kP1和kI1分别为功率控制环中PI 控制器的比例系数和积分系数。

根据式（6），可得到功率控制模型结构如图3 所示。

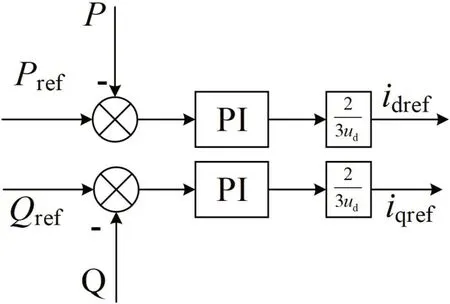
图3：功率控制模型

2.2 电流内环控制设计

将功率控制产生的电流iref作为参考值，输入电流内环中并与反馈电流比较，两者的差值经过PI 控制器的控制后产生零值稳态误差，实现对电流中非线性扰动的补偿。同时，在电流内环中增加前馈控制，来削弱电网电压对控制效果的影响。

逆变器的电压输出模型在dq0 旋转坐标系中满足[9]：

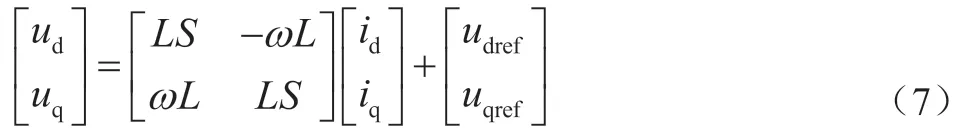
其中，S 为拉普拉斯算子，udref和uqref分别为逆变器参考输出电压。

由式（7）可知，此时的d、q 轴分量间存在耦合，无法实现对d、q 轴分量的单独控制。因此，增加前馈解耦控制，消除d、q 轴分量间的耦合关系。在解耦以及PI 控制器调节后，逆变器的模型如下所示：

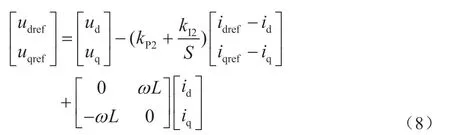
其中， kP2和kI2分别为电流控制环中PI 控制器的比例系数和积分系数。

结合式（7）和式（8），可得：

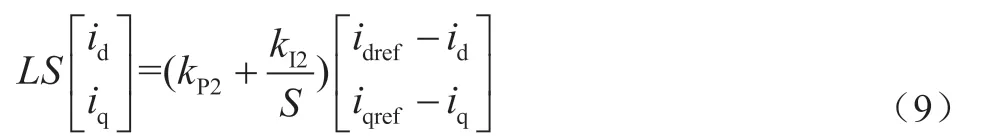
由式（9）可见，并网系统的id和iq实现了解耦，从而可以独立无差地对有功和无功电流进行跟踪控制。

根据式（8）可以搭建电流控制模型结构如图4 所示。

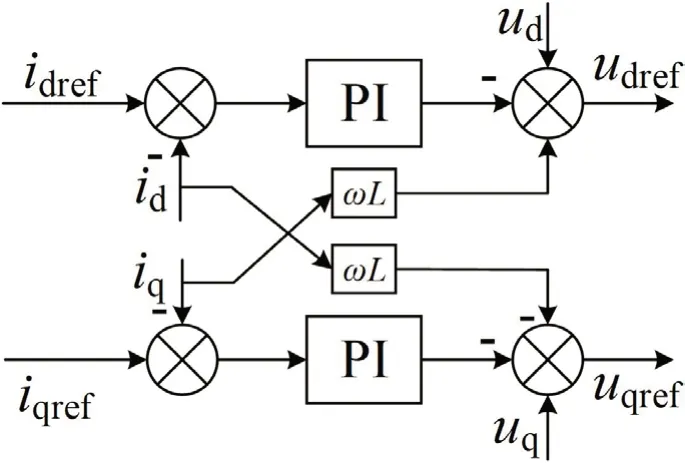
图4：电流控制模型

2.3 软件锁相环设计

软件锁相环（SPLL）通常被用来检测电压的频率与相位。其具体结构如图5 所示[10]。

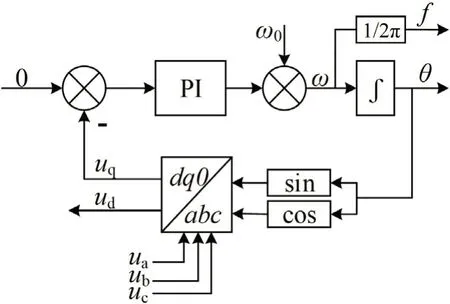
图5：SPLL 结构模型

SPLL 先将电网三相输入电压经abc →dq0 变换后，得到旋转坐标系下的d、q 轴分量ud和uq。abc →dq0 变换所用参考角度为锁相环的输出θ，uq的大小代表输出电压相位和锁相输出相位之间的差值（该值在频率完全跟踪的情况下为0）。uq与0 相减后的值经过PI 控制器后，与初始角频率ω0相加后得到锁相环输出角频率ω，再经过一个积分环节后得到最终的输出相位θ。整个系统构成一个负反馈，通过PI 控制器调节可以达到锁相的目的。

3 模拟分析

为了能够清晰说明说明PQ 控制的有效性，本文借助MATLAB/SIMULINK 软件，以图1 为基础搭建分布式电源并网模型，以图2 为基础构建PQ 控制结构。表1 给出了本文仿真所用到的参数。

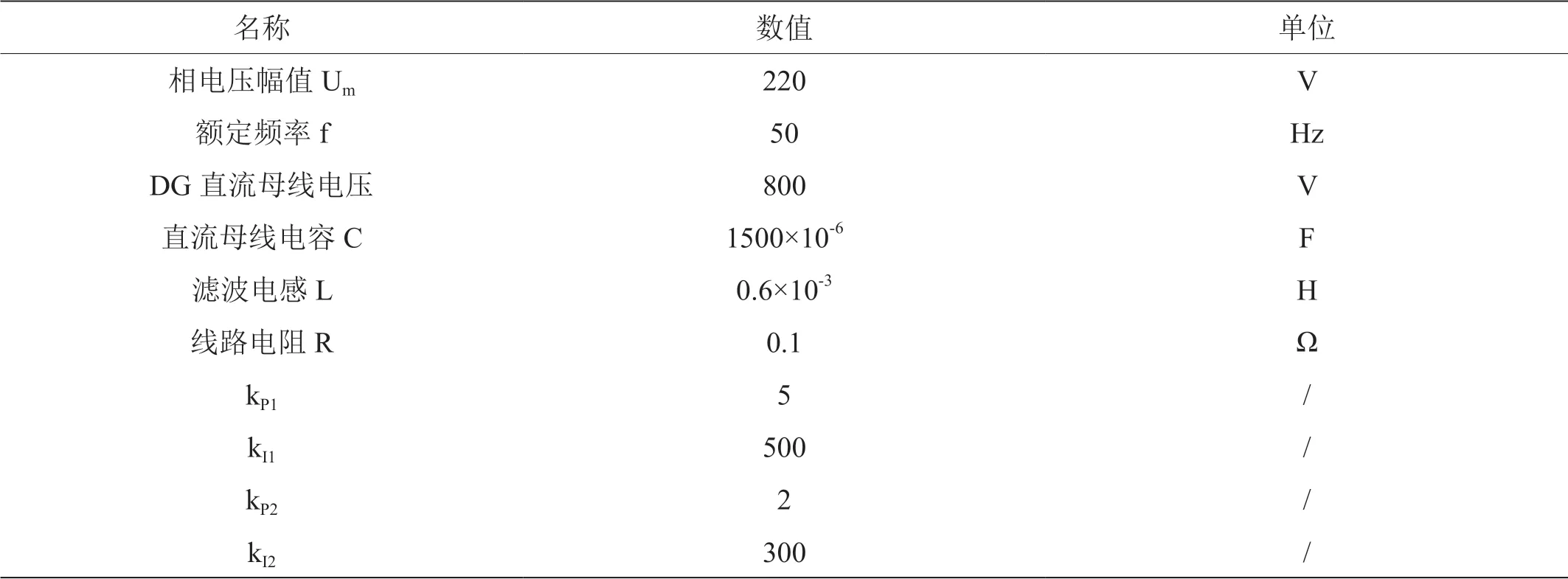
表1：PQ 控制模型参数表

3.1 负载情况下的PQ控制

这一小结主要研究DG 与主网之间的功率交换关系，为进一步的DG 并网控制打下坚实的基础。假设系统负载参数如表2 所示。

表2：负载参数表

3.1.1 增加纯阻性负载

纯阻性负载只消耗有功功率，而不消耗无功功率，多为居民负荷性质（电饭锅，电炉子、白炽灯等）。假设0.5s 时，DG 系统增加了2kW 的纯阻性负载，1s 后该纯阻性负载切除。图6 所示为此情况下DG 发出功率与电网输入功率的曲线图。

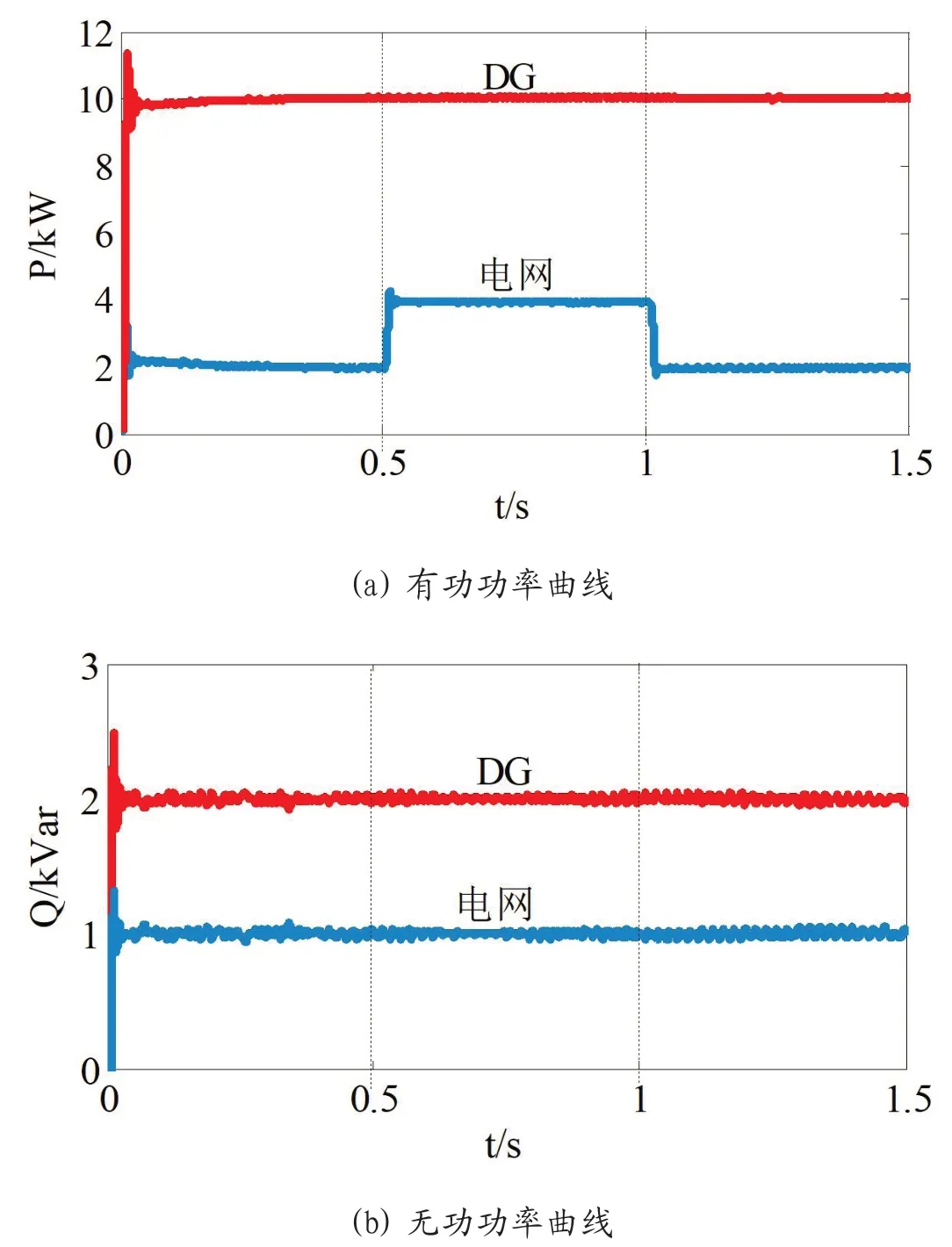
图6：增加纯阻性负载，DG 与电网的功率曲线

通过图6(a)可知，当DG的参考有功功率Pref恒定不变时，DG 的并网有功功率不会随负载功率变化而变化。图6(b)表明有功负载的变化，不会影响系统无功功率的改变。

由于DG 发出的有功功率已被完全消纳，因此由纯阻性负载所引起的功率改变全部由电网来承担。也就是说，负载所消耗的有功功率由DG 和电网共同承担。

3.1.2 增加纯感性负载

纯感性负载常见于工厂中的各种电机设备，这类负载只消耗无功功率而不消耗有功功率。假设0.5s 时，DG 系统增加了0.5kW 的纯感性负载，1s 后该纯感性负载切除。图7所示为此情况下DG 发出功率与电网输入功率的曲线图。

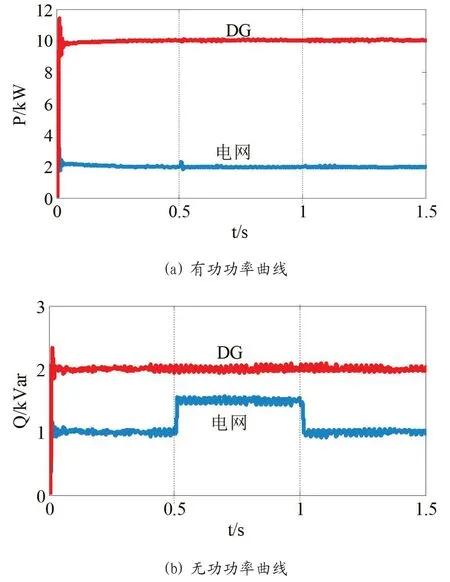
图7：增加纯感性负载，DG 与电网的功率曲线

图7 与图6 的结论基本类似，当DG 产生的无功功率的参考值Qref恒定不变时，无论负载功率如何变化，DG 所发出的无功功率也不会改变。负载所消耗的无功功率也由DG和电网共同承担。

简而言之，当负载的功率大于DG 所发出的功率时，剩余负荷的功率将由电网承担。反之，如果负载功率小于DG所发出的功率时，DG 发出的剩余功率将并入电网，由电网进行消纳。如果高比例的DG 功率进入电网，将引起电压越限和波动加剧、三相不平衡等大量问题。

4 结论

本文针对目前DG 的发展趋势，研究了DG 逆变器的并网控制。基于DG 逆变器模型，研究了PQ 恒功率控制策略。借助逆变器输出可控这一优点，实现了有功与无功功率的解耦与跟踪控制，通过对基于PQ 控制的DG 并网模型进行仿真分析，可以得到以下结论：

（1）PQ 控制可以快速准确地跟踪电网频率，保证以DG 为基础的微电网并网频率与主网同步；

（2）PQ 控制对系统的参考功率具有较快的响应以及跟踪速度，控制系统稳定，较好的实现了PQ恒功率控制的目标；

（3）并网运行时，DG 构成的微电网功率优先消纳，缺额功率由电网补足，系统的频率和电压也由电网支撑。