把握元思维 拓展新思维
——从“K型图”谈起
2022-11-16赵莹莹江苏省苏州市南环实验中学校215007
赵莹莹 (江苏省苏州市南环实验中学校 215007)
数学教育的重点是发展学生的数学思维[1].这是数学教育的重要内容,也是培养学生形成理性思维的重要组成部分之一.要教好数学就必须要注意数学思维的培养,从而提高学生的数学能力.数学是一门抽象性很强的学科,数学思维的形成不同于其他思维能力(如形象思维),不能一蹴而就,必须与直觉思维、逻辑思维、数学建模、联想迁移、类比反馈、创新意识,甚至是信念情感态度等非智力因素结合在一起,才能得到良好的效果.
数学知识的教学,要注重知识的“生长点”与“延伸点”,把每堂课教学的知识置于整体知识的体系中,注重知识的结构和体系[2].笔者认为,不仅仅数学知识的学习要注重知识的“生长点”与“延伸点”,数学思维的培养也需如此,只有在把握好学生的元思维的前提下,才能通过目标意识,逐步接近真正的解题思路,拓展新思维,从而解决更难的问题.
“K型图”是初中阶段的常见模型之一,它在研究三角形的全等、三角形的相似、直角三角形中的三角函数和平面直角坐标系中的函数图象等场合起着重要的作用.可以说,“K型图”是一首洋溢在整个初中数学学习中的圆舞曲,从初一到初三都有它的舞台.而学生对“K型图”的理解往往停留在表面,没有从根本上认识“K型图”,导致后期面对需要从深层次理解应用的难题时没有思路,无法解决.
1 关注“K型图”的元认知,把握元思维
1976年,弗拉维尔将元认知表述为“个人关于自己的认知过程及结果或其他相关事情的知识”,以及“为完成某一具体目标或任务,依据认知对象对认知过程进行主动的监测以及连续的调节和协调”[3].整个初中阶段,第一次遇到“K型图”模型是在全等三角形中:
如图1,点D,A,B在一条直线上,∠D=∠B=90°,EA⊥AC,EA=AC.求证:AD=BC.

图1
这个问题经过分析,学生很快就看出图中△EDA和△ABC是两个全等的三角形,只要证明出它们是全等的,那么“AD=BC”就能顺利地证明出来了.
第一次遇到“K型图”的数学模型,解决起来并不困难,但是从元认知的角度要将这个问题分析清楚才是关键.根据元认知理论,学生需要把握自己的认知的整个过程,而不完全是解决问题的结果.学生需要有意识地主动监测自己的思维过程,把握自己的思维的本质从何而来——“不全是利用全等,而是利用图中有的一线三垂直找两个角相等”的思维,用以明确解决这个问题的元认知,从而明白这个问题解决的本质.把握好学生的元思维才有助于解决好由这个问题延续的系列问题.
在引导学生分析后发现,从元认知出发,这其实是由于具有“一线三垂直”这个特征而形成的特殊图形,从而也引出了“K型图”模型的名称.同样,在解决问题的过程中,认清在解决“K型图”模型时的元思维过程,把握好元思维,理清了元认知,就能解决以下较难的问题:
探究:如图2,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A,B在直线l的同侧,过点A,B分别作直线l的垂线,垂足分别为点D,E.求证:DE=AD+BE.
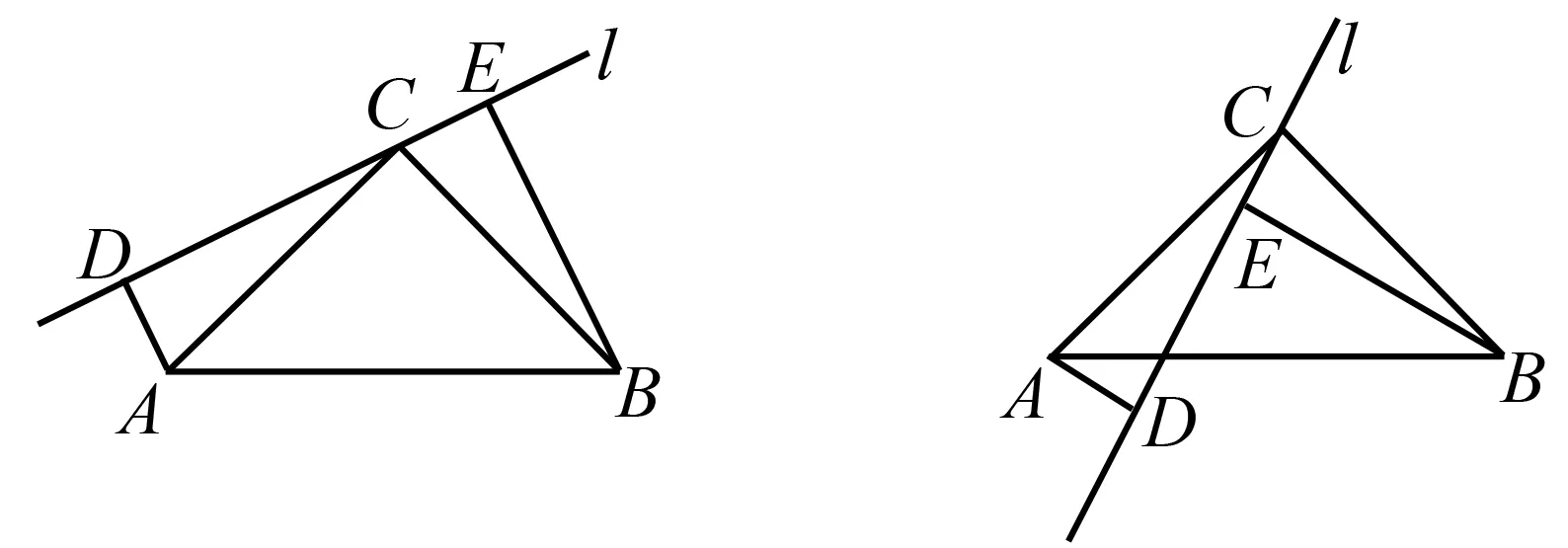
图2 图3
应用:如图3,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A,B在直线l的异侧,过点A,B分别作直线l的垂线,垂足分别为点D,E.直接写出线段AD,BE,DE之间的相等关系.
本题的探究部分,映入眼帘的就是“一线三垂直”.于是很容易想到利用AAS定理证明△ADC≌△CEB,也就是把握住自己的元思维——“一线三垂直可以找到两个角相等,再找一条边就能用AAS定理证明全等”,然后用全等三角形的对应边等量代换后得到“DE=AD+BE”.本题的应用部分是将直线l进行旋转后形成的图形,但是“一线三垂直”这一元认知依旧存在,所以可以大胆地猜测△ADC和△CEB依旧全等.经过元思维模式的思考,依旧可以利用AAS定理证明△ADC与△CEB全等,但是由于旋转后的位置不同,最后的结论为“AD=BE-DE”.
在初中许多知识点(图形模型)的学习过程也是类似“K型图”这一模型的学习过程的.所以,在学习新的知识点或者解决新的问题的时候,需引导学生关注自己对于新知识新问题的元认知,对元认知进行监控,促使学生把握好“K型图”的初始元思维.
2 关注“K型图”思维生长点,形成思维定势
由于初二数学学习的内容和初一相比更深更难,学生会不由自主地被数学焦虑所围绕,无法顺利解决数学难题.特别在学习了轴对称的相关知识后,“K型图”这一类型的问题的难度会有所提升.在了解了初一学段K型图问题解决的元认知后,在初二学段遇到K型图问题的时候,有意识地利用元认知来关注“K型图”的生长点,就可以给学生提供学习的方向,帮助学生克服数学焦虑,从而顺利解题[4].如下题:
如图4,等腰Rt△ABC中,∠C是直角,直线a,b,c分别通过A,B,C三点,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是2,则AB的长是多少?

图4 图5
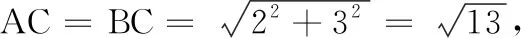
在关注了学生元认知监控和思维的生长点后,解决问题时,“通过回顾完整的答案,重新斟酌、审查结果及导致结果的途径,他们能够巩固知识,并培养他们的解题能力”[5],才能克服“K型图”带来的数学焦虑.在这里,回归到“K型图”的“一线三垂直”,就能解决这一问题.
又如:如图6,一次函数y=2x+b的图象经过点M(1,3),且与x轴、y轴分别交于A,B两点.
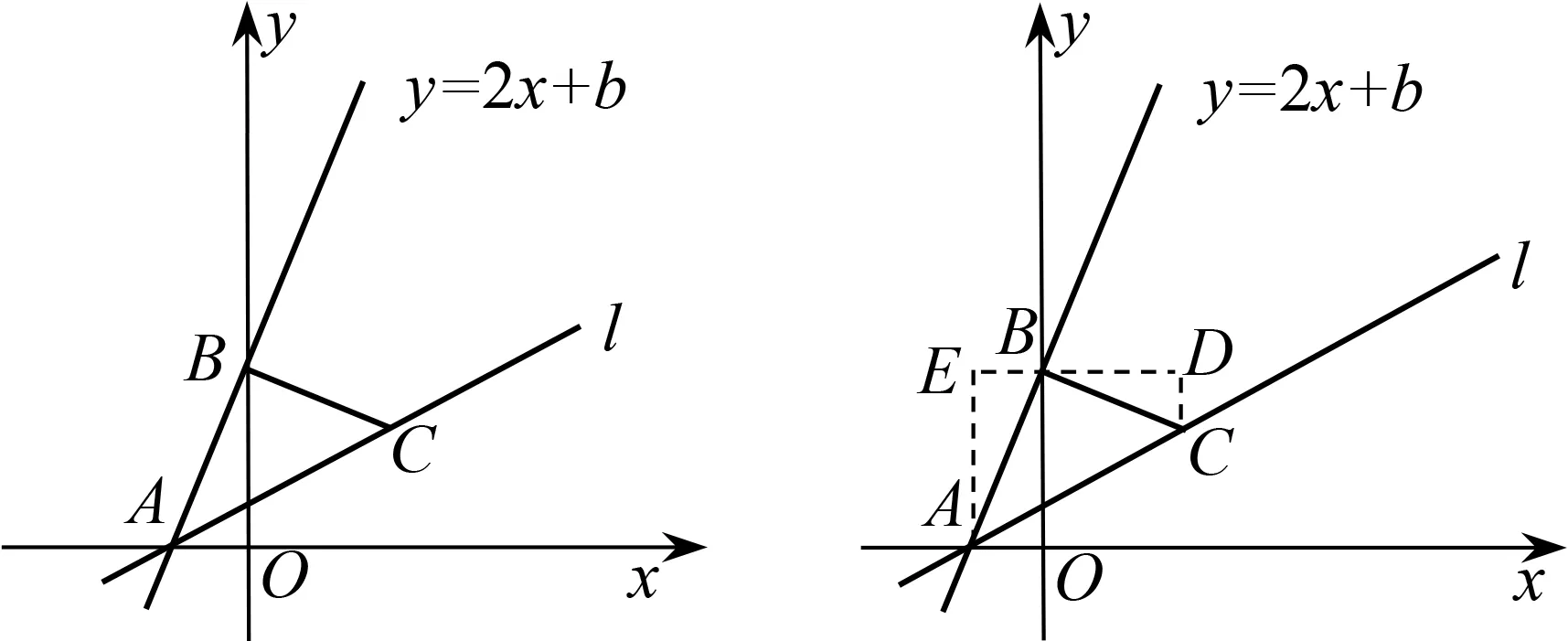
图6 图7
(1)填空:b=;
(2)将该直线绕点A顺时针旋转45°至直线l,过点B作BC⊥AB交直线l于点C,求点C的坐标及直线l的函数表达式.(2021年苏州市八年级阳光测评卷)
在这个问题中,凸显了“K型图”的“一线三垂直”的重要特征——“直角∠ABC”,并且由旋转45°后得到的等腰直角△ABC可知,这也是一个可以通过构造“K型图”解决问题的题目.如 图7,先由直线解析式求出点A和点B坐标,再由构造的“K型图”全等求出点C的坐标,从而求出旋转后的l的解析式.
数学的思维是不断发展的,形成自己的数学思维是一个长期的变化过程.所以,在形成“K型图”模型的元思维后,关注思维的生长点,就能形成自己的思维定势,也就是遇到相关特征的问题就能够想到构造“K型图”解决相关问题.
3 提炼“K型图”的核心属性,拓展新思维
进入初三学段学习了相似三角形后,“K型图”又产生了新的演变.如下题:
(1)问题:如图8,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,求证:AD·BC=AP·BP.
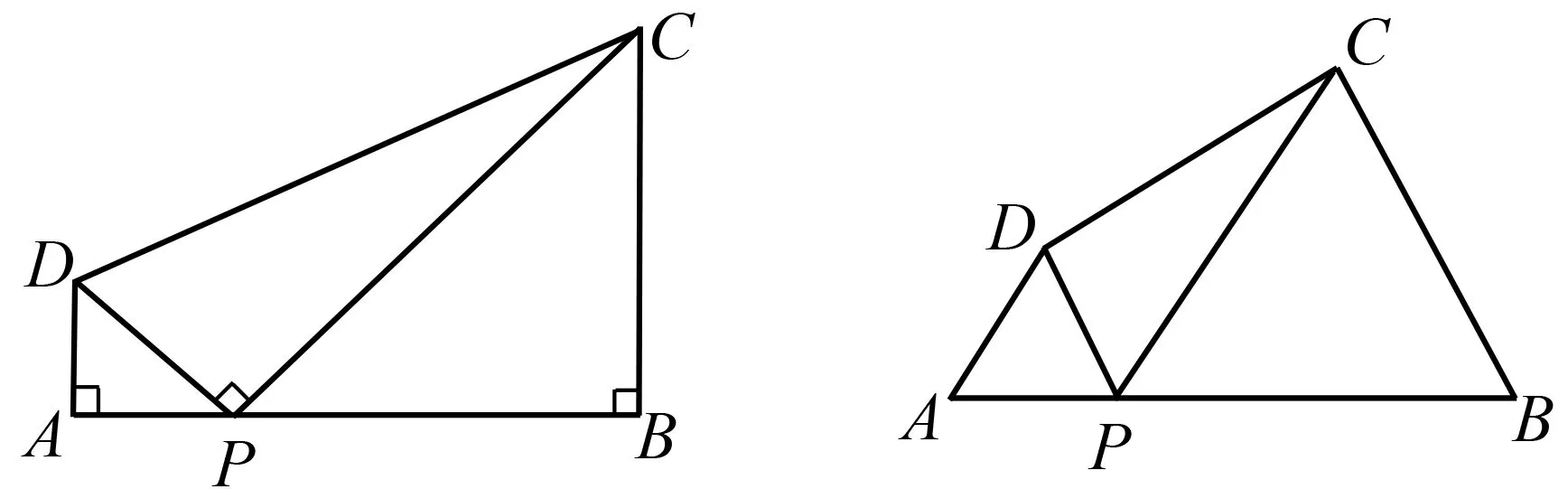
图8 图9
(2)探究:如图9,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
第(1)题只要用“一线三垂直”的模型,两角对应相等就能证明△ADP∽△BPC,然后运用相似三角形的性质解决问题.到了第(2)题,类比一线三垂直的模型并分析其原理,由于∠A=∠B,只要证明∠ADP=∠BPC就也能证明△ADP∽△BPC,然后运用相似三角形的性质解决问题.
从全等到相似,是感性思维到理性思维的飞跃,学生在解决这类问题时不能局限于“图形”,而是要关注其本质,用理性来思考才能解决相关问题.只有关注“K型图”的本质,从“一线三垂直”拓展到“一线三等角”后,才能顺利地解决问题.
又如:如图10,已知a∥b∥c,a与b之间的距离为3,b与c之间的距离为6,且a,b,c分别经过等边三角形ABC的三个顶点,则此三角形的边长为多少?
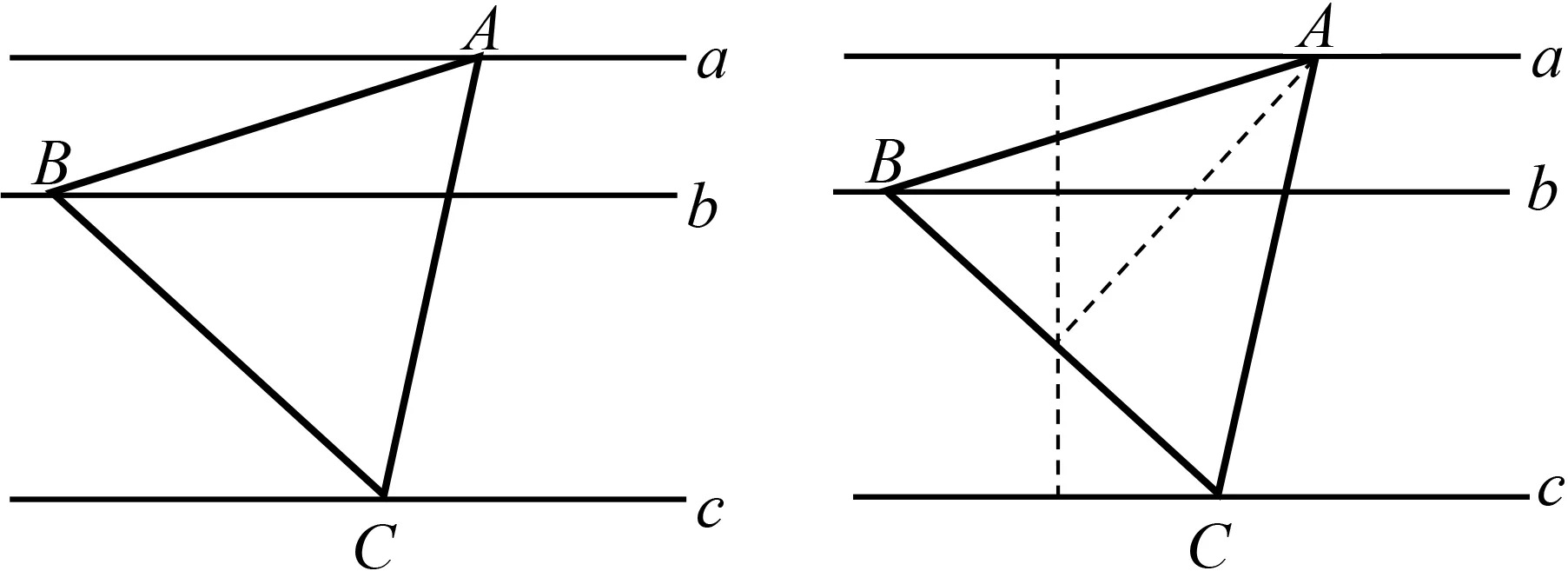
图10 图11
这是一道根本看不出可以用“K型图”模型解决问题的题目,需要在提炼核心属性后,进行数学联想才能解决问题.本题没有明显的提示,但是根据“K型图”的思维定势,需要一个角为直角,如图11,只要作等边三角形ABC的边上的高就能找到直角,然后就能化归到“K型图”的相关问题.
再如:如图12,已知抛物线y=ax2+bx+c经过点A(0,3),B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.
(1)求抛物线的解析式.
(2)如图12,动点P在直线BC下方的抛物线上,连结PO,PC,当m为何值时,四边形OPCE面积最大?并求出其最大值.
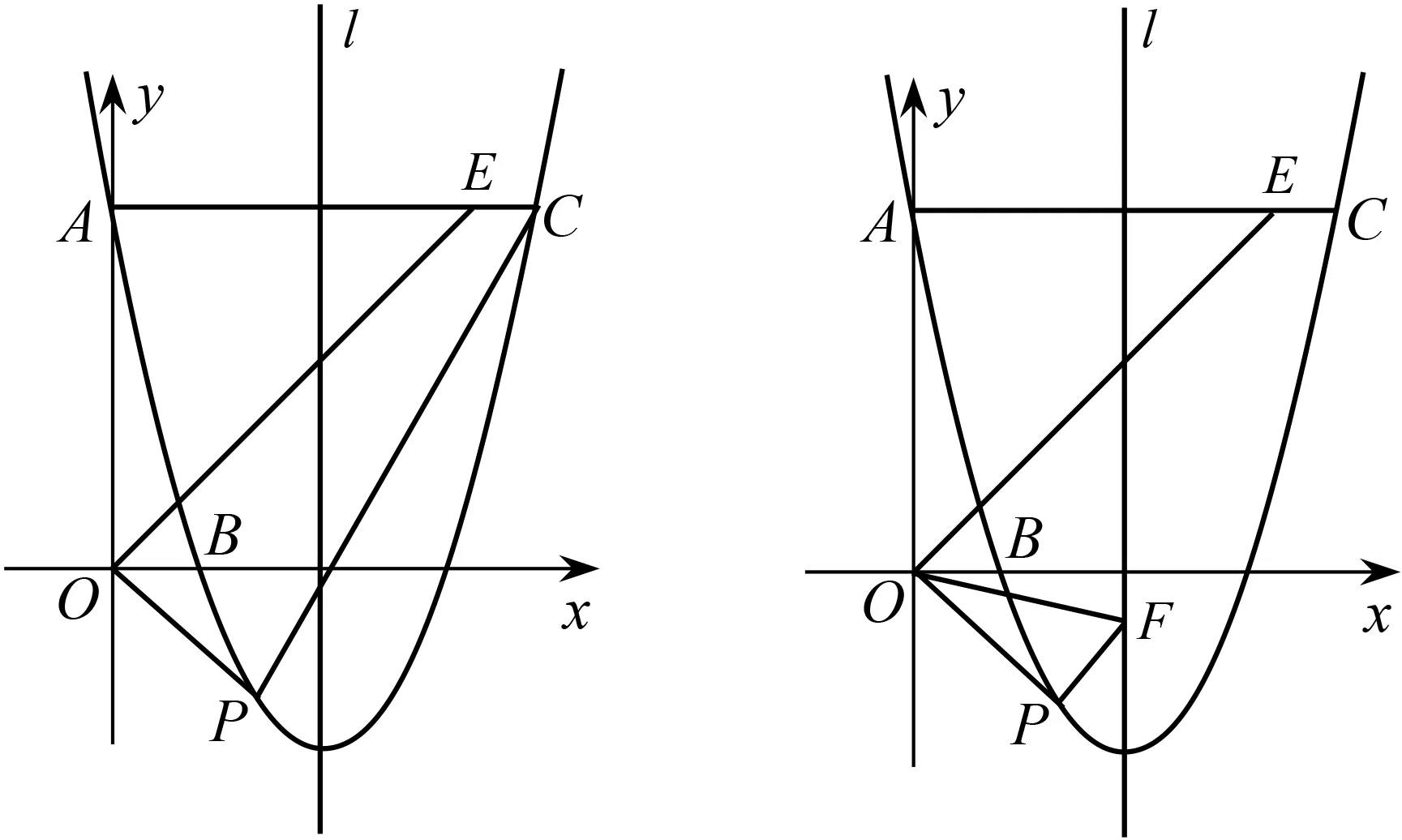
图12 图13
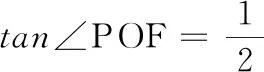
这是一道考查二次函数综合运用的中考模拟卷压轴题(选自2020年苏州中考模拟卷),最后一小题中涉及由三角函数求点的坐标.三角函数在初中学段的考查点往往结合直角三角形应用,而直角是“K型图”的核心属性之一,于是就可以构造“K型图”来解决问题.
培根说:“数学是思维的体操.”“K型图”只是初中数学学段中一个典型的模型,本文以“K型图”为例,论述了在整体教学体系中学习这个知识点的思维过程.学生从初一在学习“全等三角形”中初遇“K型图”开始,关注“K型图”的元认知,并关注“K型图”思维的“生长点”与“延伸点”,形成自己的“K型图”元思维.一旦形成了自己的元思维,在初二再遇“K型图”的时候,就能克服由于种种原因形成的数学焦虑,感受到“K型图”从全等到相似这一感性思维到理性思维的飞跃,形成“K型图”的思维定势.最终,将“K型图”的思维定势运用到综合题目中,从无到有,通过添加辅助线构造“K型图”解题,把握“K型图”的核心属性,拓展新思维.以“K型图”为例抛砖引玉,整体构建知识点的教学,培养学生发现、提出、分析和解决问题的能力,培养学生的创新思维意识,打开学生数学思维的大门,克服数学焦虑,活化数学学习.
