典型航空电连接器接触件动态性能仿真分析

刘 琦，郁大照，许振晓，王 琳

（1.海军航空大学，山东 烟台 264001；2. 92279部队，山东 烟台 264003）

电连接器广泛应用于现代飞机系统中，为各设备之间传递动力和信号发挥了重要的枢纽作用。航空电连接器在工作时始终处于动态环境之中，很容易受到外界振动、冲击、电流和温度变化等因素的影响而发生接触界面上的微动现象[1]。但由于接触件隐藏在电连接器壳体内部，而且微动行为具有一定的隐蔽性，导致人们难以监测和复现微动腐蚀行为的发生和发展。判定电连接器在工作状态甚至是极限工况下是否会发生微动，在外界交变载荷激励下会发生什么样的响应，往往是开展微动问题研究的前提和基础。

解决方法之一就是利用有限元仿真对接触件进行建模，以工作条件下的载荷和约束作为边界条件，分析接触件的接触区域变形和应力情况。Santosh V.Angadi等[2]综述了当前电连接器有限元仿真方面取得的进展，介绍了电接触本体区域和接触区域的微动仿真主要成果；George Flowers 等[3-4]针对叶片插头/插座连接器系统在轴向振动激励下的微动现象开展了系列试验和仿真研究，对具有不同长度连接线的连接器系统在不同频率下的单频振动阈值振幅进行了评估，证明了轴向振动激发的微米级振幅足以触发电连接器的微动退化；Ibrahim等[5]利用Abaqus软件对单个叶片插头/插座连接系统建立2D 模型并进行了微动分析，研究了温度和热循环对振动诱发微动的影响。Zhi Zeng等[6]对Micro-D电连接器进行了力学模型、动力学分析和插拔力实验测试,分析了结构参数对插拔稳定性的影响；潘骏等[7]对Y17P-1604 电连接器接触件进行正弦和随机振动仿真，得到了相对位移和应力的变化规律，建立了基于Wiener过程的接触电阻退化模型；骆燕燕等[8-10]利用有限元仿真研究了振动应力和冲击应力对电连接器性能的影响，研究了接触件在不同振幅、频率、脉冲持续时间和峰值加速度等因素作用下的响应，认为导致接触性能退化的主要原因是应力松弛和微动磨损；郁大照等[11-13]使用ANSYS 和COMSOL软件联合仿真，计算了振动条件下的接触件力学和电学性能，认为电连接器在受到垂直振动时的电阻峰值要高于水平振动；王龙泉[14]、闫冰[15]、蒋杰[16]等在其硕士论文中运用有限元仿真和试验研究等方法研究了电连接器的振动特性和热特性问题，讨论了簧片长度、厚度和缩口量等因素对接触性能的影响。

本文在上述工作的基础上，采用有限元仿真技术对飞机上常用的J599Ⅲ系列22D 型接触件进行了建模和仿真分析，结合产品性能参数和实际使用工况，对其动态性能进行系统的研究分析，为后续微动问题研究打下理论基础。

1 接触件力学建模

J599Ⅲ系列电连接器接触件为针孔配合形式，插针形状为头部倒圆的圆柱，插孔为圆形开槽缩孔式结构，插孔簧片呈椭圆形闭合。插针与插孔处于插合状态时，插孔由于开槽两侧的簧片被撑开而发生弹性变形，产生向内的压力夹紧插针，接触件变形示意图，见图1。将插孔簧片简化为悬臂梁结构，则单侧簧片变形后产生的接触压力为：

图1 接触件变形示意图Fig.1 Schematic diagram of deformation of contact assemblies

式（1）中：L为悬臂有效长度；δ为y向等效变形量；E为材料的弹性模量；I为插孔簧片截面关于中性层轴的惯性矩。

插针插拔的受力过程可分为3 个阶段：插合时插针头部半圆与插孔簧片的接触过程；插针圆柱体与插孔簧片的接触过程；拔出时插针头部半圆与插孔簧片的接触过程。假设插孔固定，插针在力Fi的作用下缓慢移动，第1阶段的插针的受力情况，如图2所示。

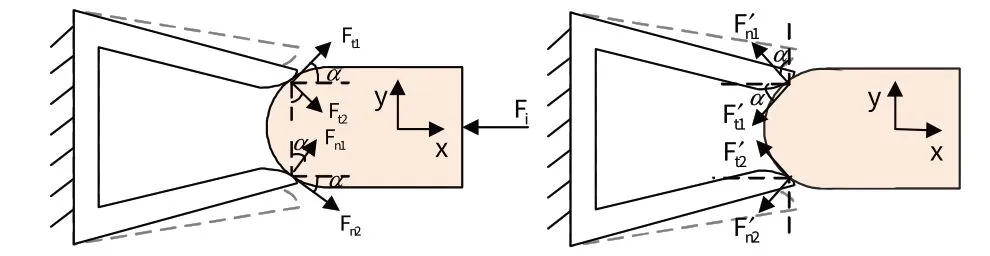
图2 插针插孔受力分析简图Fig.2 Schematic diagram of force analysis of a pin and jack

插孔对插针的作用力可分解为垂直于接触面的Fn和平行于接触面的Ft，设接触面间的摩擦系数为μ，则有Ft=μFn。接触件结构关于xoz平面对称，因此插针在y方向的受力自然平衡。插孔左端固定，x方向受力由支座反力平衡，y方向受力依靠簧片变形平衡。插针与插孔的平衡方程分别为：

式（4）中，r1和r2分别为插针头部半圆半径和插孔簧片端部倒圆半径。插入量sin与α的关系为：

假设插针与插孔发生的是无黏着接触，接触区平面形状为长轴和短轴分别为a、b的椭圆形。按照Hertz接触理论，可将插针与插孔的横截面接触区模型转化为2 个曲面弹性体之间的接触，将轴截面接触区模型转化为球体与弹性半空间体的接触，如图3所示。

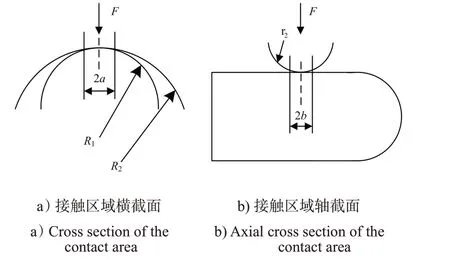
图3 插针与插孔接触简化模型Fig.3 Simplified model of the contact between pin and jack

根据文献[17]，可知接触区轴截面的接触半宽b为：

式（13）中：M为质量惯性矩阵；C为阻尼比矩阵；K为刚度矩阵；f为广义力矩阵；x为广义坐标向量。

假设系统仅发生一维振动（分别简化为径向振动和轴向振动），将插针、插孔、插针座和插头座简化为质量块，并根据连接关系设定刚度系数和阻尼系数，原理图和对应的参数，如图4所示。

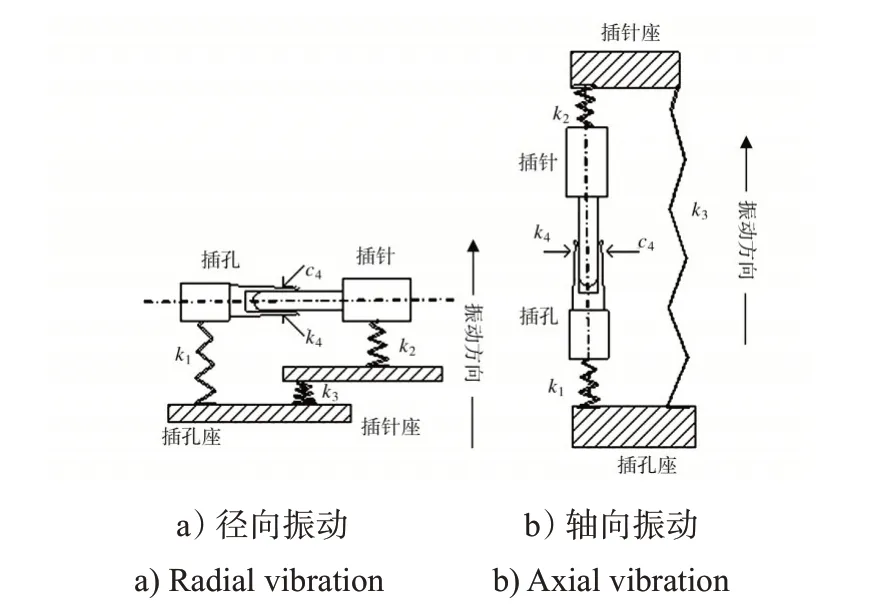
图4 电连接器一维振动原理图Fig.4 Schematic diagram of the one-dimensional vibration of the electrical connector

不论接触件受到轴向还是径向的振动激励，其动力学模型在数学表达形式上是一致的，只是对应的刚度系数或阻尼系数大小不同。弹簧刚度在插针座与插孔座、插针与插针座、插孔与插孔座之间起主导作用，不考虑它们之间的阻尼，插针和插孔之间有弹簧和阻尼，则该四自由度阻尼系统的动力学微分方程为：

从式（15）可以看出，相对位移值的变化是1 个与其他部件振动耦合的二阶振荡过程。

2 插拔仿真与结果分析

根据接触件尺寸参数建立3D 几何模型，导入Workbench平台进行前处理。22D接触件的规格参数和材料属性分别见表1 和表2。将插针和插孔的接触区域进行切分，设置接触类型为摩擦，参照文献[18]将摩擦系数设置为0.1295，接触行为选择非对称，算法选择增广拉格朗日算法。为接触区域单独设置网格细化，接触件几何模型和接触区网格，如图5所示。

表1 接触件的规格参数Tab.1 Specifications of the contact assembly

表2 接触件基体材料属性Tab.2 Properties of the contact material

图5 接触件几何模型和接触区域网格Fig.5 Geometric model of the contact assembly and mesh of the contact area

为保证计算收敛和求解精度，将整个分析过程分为5 个载荷步：第1 步，在插孔上、下簧片边缘分别施加向内的收口力，使插孔取得预定的收口量，这里取1 N、1.4 N 和1.7 N 三种情况进行研究，同时插针向前移动0.2 mm，使其与插孔之间的距离尽量缩短；第2步，插针向前移动0.3 mm，使其与插孔建立稳定的接触；第3步，插针继续向前移动1 mm，达到插针圆柱部分与插孔稳定接触的阶段；第4步，插针退出1mm；第5步，插针继续退出0.3 mm，与插孔完全脱离接触。由于涉及刚体位移，需要打开大变形开关。

通过计算得到不同收口力对应的几何和力学参数，如表3所示。收口力不断增大，簧片的收口量也随之增大，因此插针插入时作用在插针上的压力、接触面积、接触面反力和插拔力都会变大。

表3 不同收口力对应的几何和力学参数Tab.3 Geometric and mechanical parameters corresponding to different closing forces

利用探针工具，求得3 种情况下插拔过程中施加在插针上的支反力，即插拔作用力，如图6所示。

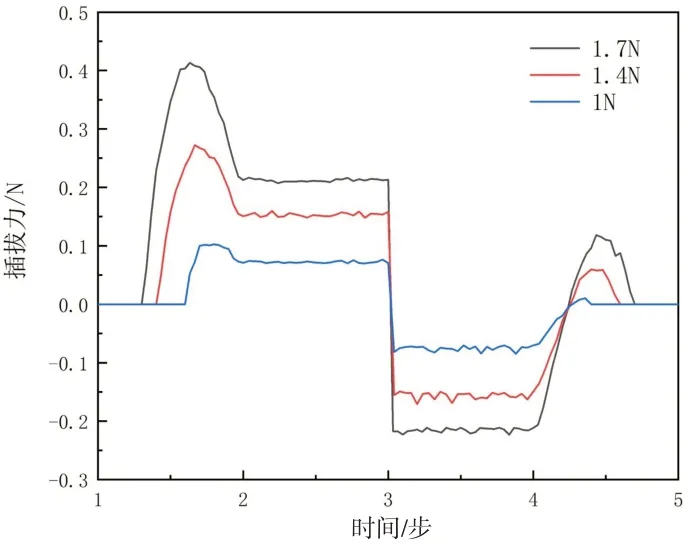
图6 插拔力Fig.6 Inserting and pulling forces

在插入时，不同收口量对应的初始接触时间不同，插入力值随着插孔簧片挠度增加而迅速增大，在约第1.6 s 时达到最大值，然后下降并趋于稳定，这表明插孔簧片已与插针圆柱部分建立稳定接触。在拔出时，拔出力开始保持稳定，然后迅速减小，与接触面作用力的x向分力共同推动插针向外运动。利用接触工具求得接触过程中的摩擦应力，摩擦应力与插拔力变化规律一致，峰值出现时间相同。插入力和摩擦应力在插拔过程中均呈现先增大再减小的趋势，主要原因在于，在最大值处作用在接触区的等效应力最高，且此时材料变形引起的接触区域面积较大。接触区域近似不对称的椭圆形，触点内部中心区域压应力最大，向四周扩展并逐渐减小。综合比较，1.4 N 时的收口量和插拔力与产品实测值最为接近，因此，选择此情形下的计算结果作为后续的分析基础。

3 振动特性仿真与结果分析

3.1 模态分析

通过模态分析能够确定接触件的固有频率和振型，预测构件在振动激励下的响应。在进行其他动力学分析之前，首先，要进行模态分析，在建模软件中完成插针与插孔的装配；，然后，导入Workbench 中有预应力的模态分析模块，在插孔簧片处施加压力使插口收口；最后，进行模态求解。模态分析只涉及线性分析过程，求解过程不涉及接触状态的改变，因此，设置接触类型为不分离。构件的振型和频率受约束影响很大，本文根据实际应用情况分别在插针和插孔与绝缘体接触的固支点处设置固定约束。

求解得到接触件的前6 阶固有频率和振型图，分别如表4和图7所示。

表4 接触件固有频率Tab.4 Inherent frequencies of the contact assembly

图7 接触件前6阶振型图Fig.7 First sixth-order modes of the contact assembly

接触件的前2 阶固有频率数值相差不大，对应的振型分别为插针和插孔接触端保持相同的y向和z向运动，且振幅近乎一致；第3阶和第4阶固有频率数据大小较为接近，对应的振型分别为插针和插孔接触端保持方向相反的y向和z向运动，运动过程中始终保持接触状态；第5 阶和第6 阶固有频率对应的振型分别为插针和插孔各有1 个节点的y向和z向运动，方向相同但振幅相差较大。

3.2 谐响应分析

谐响应分析主要用于分析构件在不同频率的简谐载荷作用下的稳态响应。在上一步模态分析结果的基础上，加入谐响应分析模块。根据航空设备振动试验参考频率设置扫频范围为0～2 000 Hz，根据产品手册性能指标设置加速度极限载荷为60 g，方向为z向。最大变形和应力均发生2 000 Hz 时，最大变形为0.517 μm，发生在插针末端，如图8 所示；最大应力发生在接触点处，如图9 所示。若将同样的载荷加载在x方向时，计算得到的最大变形量仅为2.83×10-6mm。

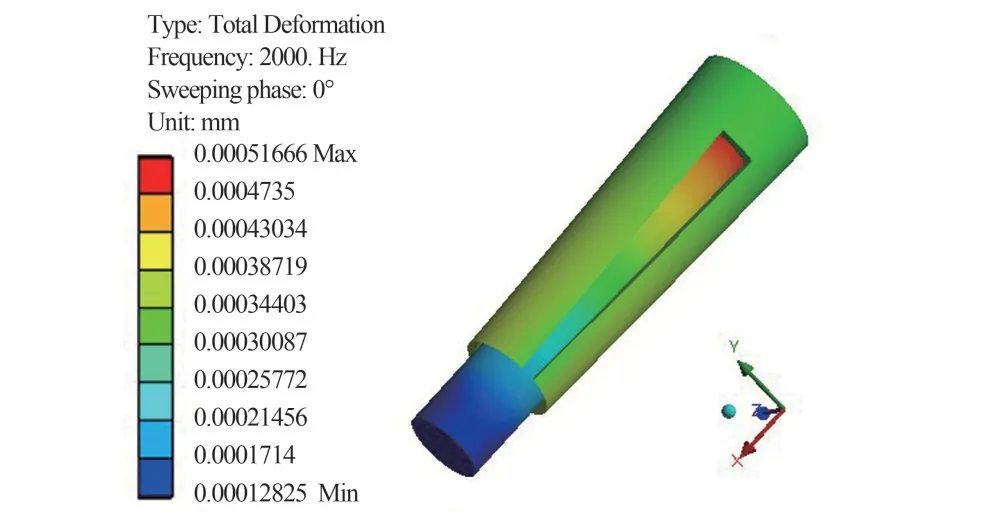
图8 接触件在简谐载荷作用下的变形Fig.8 Deformation of the contact assembly under harmonic load

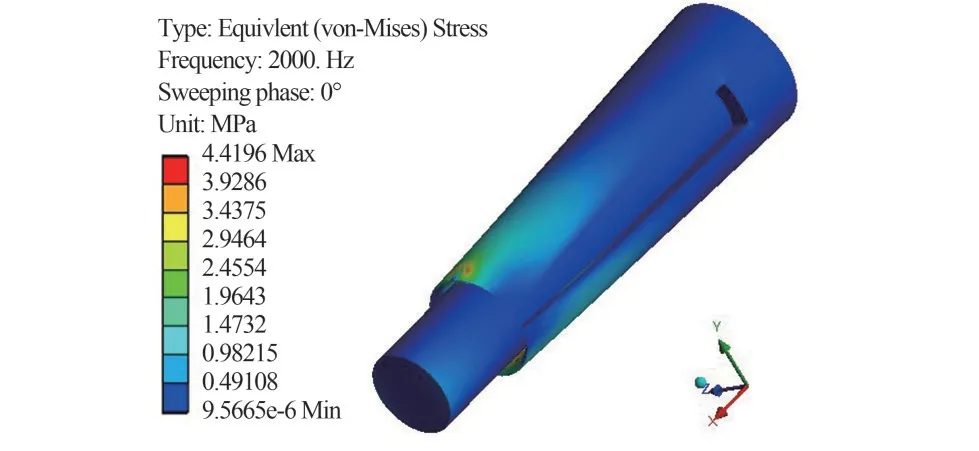
图9 接触件在简谐载荷作用下的应力Fig.9 Stress of the contact assembly under harmonic load

3.3 随机振动分析

通过随机振动分析，可以知道构件在不同的频率和谱值作用下的响应，确定构件响应的统计特性。它与谐响应分析的主要区别是谐响应有单一主频，而随机振动是给定的频率范围，利用功率谱密度（PSD）曲线来描述随机激励的统计特征。随机振动分析也要在模态分析的基础上进行。

本文研究了接触件在2种工况下的激励响应：第1种是根据航空设备振动试验功率谱施加的激励，对应的加速度功率谱密度，如图10 所示；第2 种是根据产品手册施加的极限工况，频率100～2 000 Hz，功率谱密度5 g2/Hz，方向均为z向。

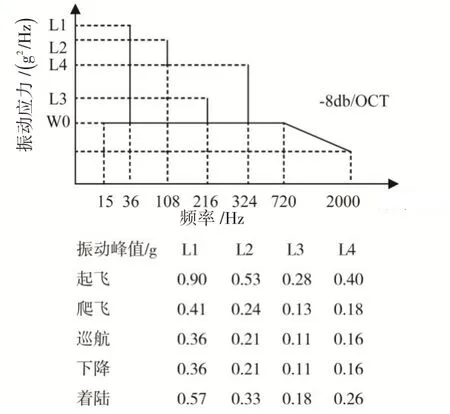
图10 航空设备振动试验条件参考Fig.10 Reference for vibration test conditions of the aviation equipment

取3σ作为截断上限，接触件在2种工况下的变形和应力结果,如图11～14 所示。第1 种工况下的构件z向最大变形为0.465 μm，与上一步谐响应分析中的变形大小在同一量级，同样的载荷加载在x方向时，计算得到的最大变形量仅为3.90×10-5mm，最大应力值为3.04 MPa 。第2 种工况下的构件z向最大变形为2.40 μm，最大应力为21.63 MPa，若将此载荷施加在x方向上，则得到的最大变形为1.38×10-5mm，最大应力值为0.29 MPa。不论施加哪种工况，最大应力均发生在接触件触点处。

图11 接触件在第1种工况下的变形Fig.11 Deformation of the contact assembly under the first working condition

图12 接触件在第1种工况下的应力Fig.12 Stress of the contact assembly under the first working condition

图13 接触件在第2种工况下的变形Fig.13 Deformation of the contact assembly under the second working condition

图14 接触件在第2种工况下的应力Fig.14 Stress of the contact assembly under the second working condition

综合以上动力学分析过程可以看出，接触件的结构固有频率起始于7 874.3 Hz ，明显高于工作载荷0～2 000 Hz 的振动频率，因此，判断接触件在服役中不会受到共振问题的影响。简谐激励和随机振动载荷施加在接触件径向（z向）时，构件发生了微米级的变形，而且接触点处应力集中现象较为明显，表明接触点处可能发生微动磨损。而同样的载荷施加在轴向（x向）时，变形仅为纳米级，对比说明，接触件受径向振动影响更大。

4 热-结构耦合仿真与结构分析

电连接器接触件在工作中不仅受到振动的影响，而且受到环境温度和电流的影响。不同环境和时段的温差会导致构件温度变化，电流流过构件也会导致电连接器内部温度升高。本节即考察接触件接触面在温度升高后的相对滑动情况。

首先，将装配好的接触件模型导入结构分析模块，按照上一节的分析步骤为模型加载约束和载荷，此步的目的是使插针和插孔建立稳定的接触。求解完成后，在模型树上点击鼠标，选择“Update Geometry From Results File”，使模型更新为变形后的形状。设定环境温度为25 ℃，依据航空设备工作环境温差值加载温度变量，使构件温度依次升高10 ℃、15 ℃和20 ℃。最后进行热-结构耦合分析，在固支点处设置固定约束，导入前一步的温度分布结果，计算得到不同温差下的插针与插孔接触处界面的轴向滑移量，如表5所示。

表5 接触件接触界面在不同温差下的轴向滑移量Tab.5 Relative slip of the contact interface under different temperature differences

轴向滑移量已经达到微米级，分别为4.58 μm、6.40 μm 和8.15 μm，且随着温度升高而增加。温度载荷作用下的轴向变形量明显大于接触件在谐响应和随机振动情形下的轴向变形量，说明温度载荷对接触界面产生相对滑移/变形的影响更大。

5 结束语

微动是1 个动态的瞬时过程，电连接器内部发生的微动行为难以通过技术手段进行观测，而微动造成的磨损等问题却不容忽视。本文通过力学建模和有限元仿真方法，分析了接触件在不同载荷和工况下的动态响应，结果证明了接触件在特定的冲击、振动和温升条件下会发生微动问题，为后续的微动研究提供了理论根据。仿真结果还表明：接触件的插入力和摩擦应力在插拔过程中均呈现先增大再减小的趋势，接触区域近似不对称的椭圆形；该接触件的固有频率较高，在正常振动工况下不会发生共振问题；在谐响应和随机振动分析中，接触件径向变形受振动作用影响比轴向更大；接触界面轴向滑移量受温差工况的影响要大于受振动工况的影响。微动导致接触件表层金属微动产生微动腐蚀问题，进而使电阻升高，影响信号传输。整个过程的影响因素和微观机理应是下一步研究的重点之一。