不确定伺服系统的模糊自适应NTSM控制

李方俊，王生捷，李 浩

（北京机械设备研究所，北京 100854）

传统的永磁同步电机位置伺服系统一般采用三闭环控制结构，内环为电流环，次环为速度环，最外环为位置环，PID 是环路控制器最常用的设计方法[1-3]。但是，传统的PID控制器参数调节复杂，系统响应速度慢，在面对系统结构参数不确定或者时变、非线性和负载变化时，难以达到理想的控制效果[4-5]。近年来，许多先进的控制算法在不确定永磁同步电机伺服系统中得到了应用，如：采用自适应反步控制的方法对系统未知参数进行估计并利用滑模控制来保证系统对未知扰动的鲁棒性[6]；采用自适应模糊滑模控制的方法对系统存在的抖振问题进行抑制[7-10]。然而，上述的控制方法存在一定的不足之处，例如：采用反步法设计控制器结构时，会存在“项数膨胀”的问题，这将导致所设计的控制输入量特别大，实际控制系统难以实现；传统的滑模控制器均采用线性滑模面，理论上系统状态不仅难以在有限时间内收敛到给定轨迹，而且滑模控制器还存在固有的抖振问题，为了得到良好的抗扰能力，传统的滑模控制器不得不将扰动上界值取得偏大，这却加剧了系统的抖动。

为了简化控制器的设计和提高伺服系统的快速性和鲁棒性，本文在研究不确定伺服系统模糊自适应滑模控制的基础上，引入了非奇异终端滑模面，这保证了伺服系统在面对结构参数和负载变化鲁棒性的基础上，拥有了更快的响应能力。同时，为了进一步提高系统的控制精度，缩小跟踪误差的波动范围，设计了1 种结合误差积分项的非奇异终端滑模面，为了便于算法在数字控制系统中得以实现，均采用离散化仿真方式。

1 伺服系统数学模型

永磁同步电机伺服系统的位置机械方程，如下所示：

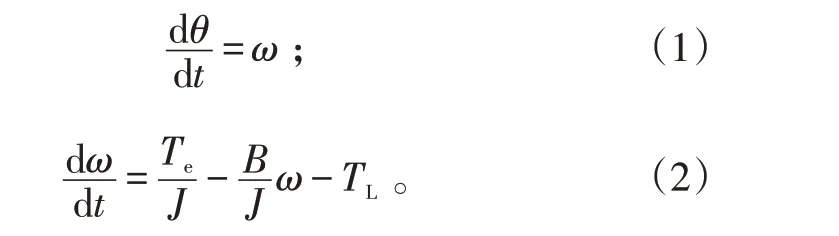
式（1）（2）中：θ表示电机转动的机械角度；ω表示电机的机械角速度；Te为永磁同步电机的电磁力矩；J为折算到电机轴端的系统转动惯量；B为摩擦系数；TL为负载和扰动力矩。

表贴式永磁同步电机的数学模型为：

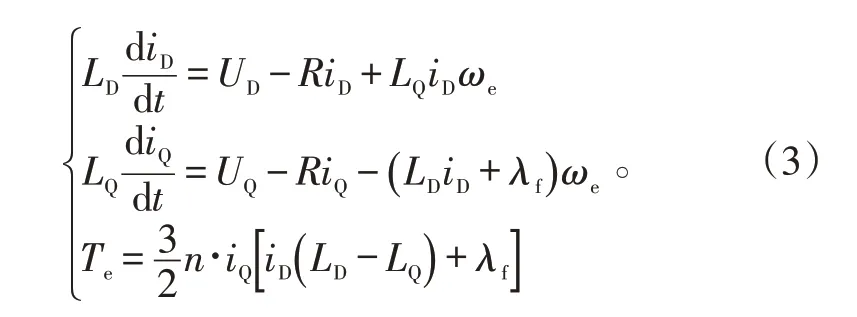
式（3）中：ωe为电机电角速度；iD、iQ为电机DQ 轴的定子电流；LD、LQ为电机DQ 轴电感；R为电机相电阻；UD、UQ为相电压；n为永磁同步电机极对数；λf为电机转子磁链。

如图1 所示，所设计的永磁同步电机伺服控制系统采用双闭环控制结构，外部跟踪指令信号通过所设计的控制器解算为Q 轴电流信号直接控制电流环，使传统的PID 位置伺服系统三闭环的控制方式得以简化，从而提高了伺服系统的响应速度。

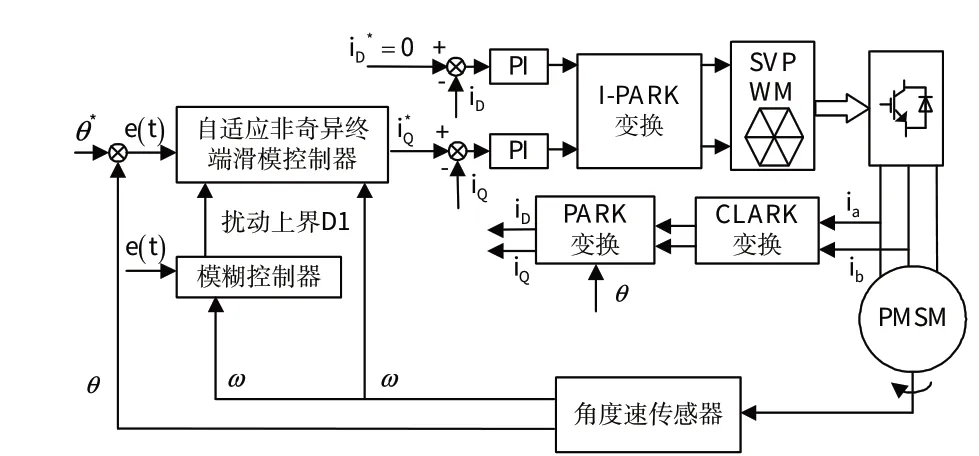
图1 伺服系统控制框图Fig.1 Control structure of the servo system

电流误差经PI控制器处理后为电机DQ轴电压信号，采用空间矢量脉宽调制（SVPWM）技术将电压信号转变为逆变器开关管的PWM 斩波信号传递给电机。

2 自适应非奇异终端滑模控制器设计

式（6）中：β ＞0 是设计常数；p和q是奇数，且q ＜p ＜2q。

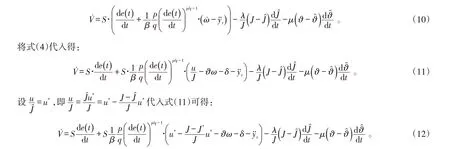
当非奇异终端滑模面S=0 时，解方程可得：

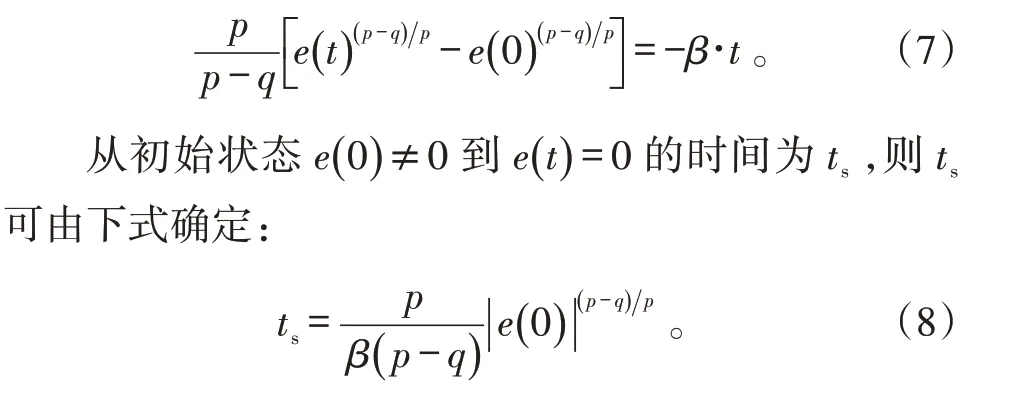
系统误差将在有限时间ts内收敛到0。

与传统的线性滑模面相比，非奇异终端滑模面由于引入了非线性项，故拥有更快的收敛速度，系统将在有限时间内到达滑模面[11]；与普通的终端滑模面相比，非奇异终端滑模面避免了出现控制输入无穷大的情况，即系统的奇异现象。线性滑模面与非奇异终端滑模面的收敛速度，如图2所示。

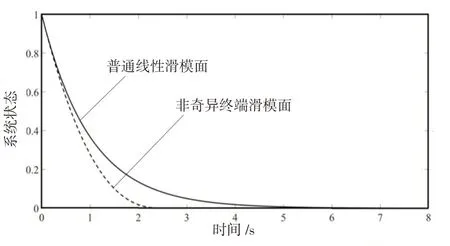
图2 非奇异终端滑模面与普通线性滑模面收敛速度的比较Fig.2 Comparsion of the convergence speed of NTSM with that of linear SMC

为了满足系统稳定可达性的条件，Lyapunov函数设计为：

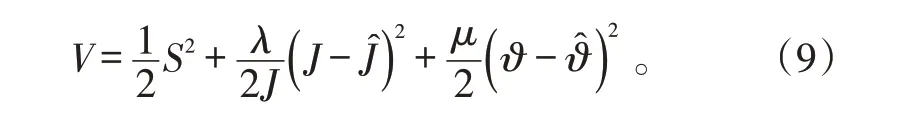
式（9）中：λ和μ为正比例系数；J^ 为系统转动惯量J的估计值；ϑ^ 为系统结构参数B J的估计值。

对式（9）求导可得：

3 模糊控制器设计

滑模控制器的设计往往需要已知未知扰动上界的大小。实际伺服系统中扰动形式多样，这给控制算法的设计带来了极大的困难，工程上往往将上界值D1取值较大以保证伺服系统的鲁棒性，然而较大的上界值又会造成系统的控制输入的剧烈抖动，这可能会激起整个伺服系统的共振。为了合理设计扰动的上界值D1，现采用模糊控制的思想对扰动上界值进行估计[12-13]。

滑模状态存在的条件为S·S˙＜0，为了使系统在扰动作用下能达到滑模面，现制定如下的模糊规则：

其中，NB 为负大，NM 为负中，NS 为负小，ZO 为0，PS 为正小，PM 为正中，PB 为正大。根据工程经验，将输入S·S˙和输出D1 的隶属度函数定义为三角形的隶属度函数。图3 和图4 为输入S·S˙和输出D1的隶属度函数分布图。

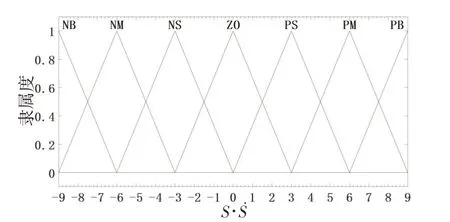
图3 模糊控制器输入隶属函数分布图Fig.3 Distribution diagram of the input membership function of the fuzzy controller

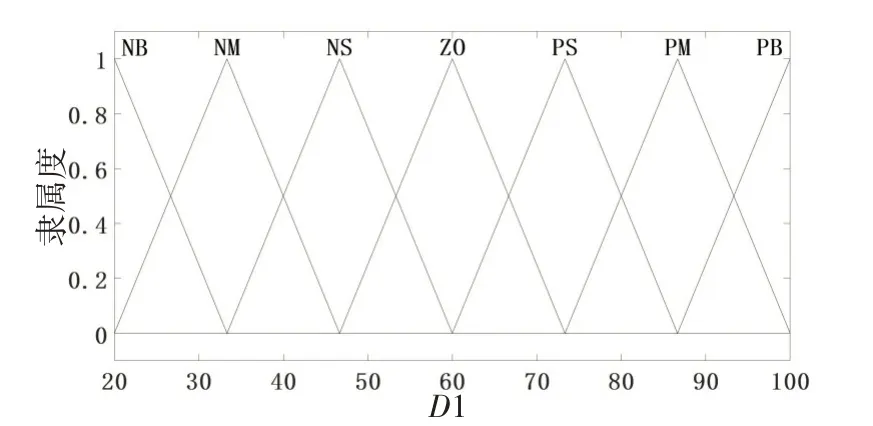
图4 模糊控制器输出隶属函数分布图Fig.4 Distribution diagram of the output membership function of the fuzzy controller

根据滑模控制理论：当S·S˙＞0 时，代表系统不具备滑模控制的可达性条件，需要加大D1 来提高收敛速度和补偿干扰；当S·S˙＜0 时，代表系统已具备可达性条件，可以适当减小D1 值，降低系统输入的抖振。基于以上分析，按式（21）（22）建立模糊规则。

模糊控制器通过采用Mamdani推理法，采用重心法进行反模糊化处理后，得到扰动上界的模糊估计值。

4 误差积分非奇异终端滑模面设计

只有在连续的系统中才存在理想的滑动模态，对于离散系统，系统会在一定范围的切换带内进行准滑动模态运动,如图5所示。

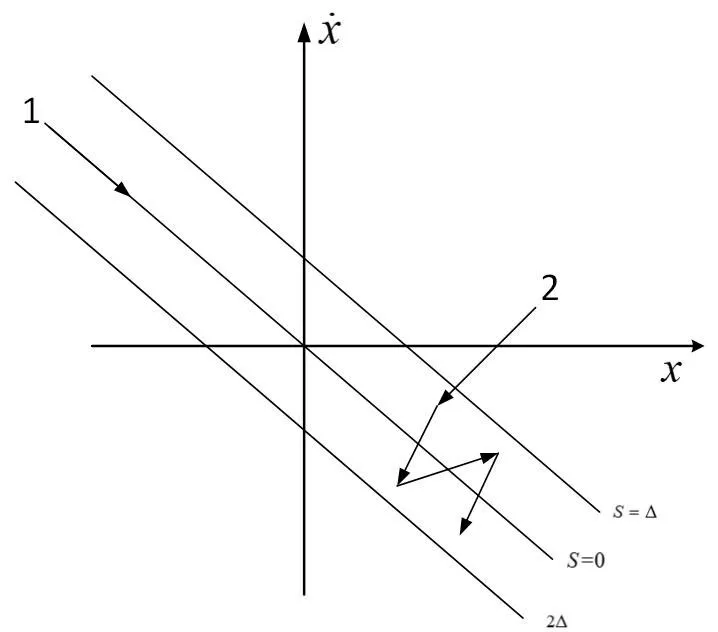
图5 连续和离散滑动模态Fig.5 Continuous and discrete sliding mode

图5中：曲线1为连续系统理想的滑模状态；曲线2为离散系统的准滑模状态；2Δ为离散滑模面切换带宽度[14]。

从图中可知，相比于连续的控制系统，离散的非奇异终端滑模控制方法会有跟踪误差的存在，因此，为了进一步改善离散模糊自适应非奇异终端滑模控制器的控制精度，将PID 控制器中对误差积分的思想引入控制器的设计当中，构造了1 种新型的误差积分非奇异终端滑模面：

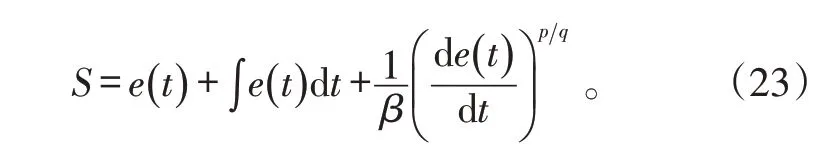
由于误差积分项的作用，离散系统将在达到稳态时拥有更好的稳态精度。

5 控制系统建模与仿真分析

采用MATLAB/Simulink 搭建传统PI 控制系统、自适应滑模控制系统、模糊自适应非奇异终端滑模控制系统和新型模糊自适应非奇异终端滑模控制系统的仿真模型。仿真中采用的表贴式永磁同步电机的参数为：定子电阻R=0.34 Ω ；直轴电感和交轴电感LD=LQ=0.006 H；转子磁链λf=0.243 Wb；电机初始转动惯量J=0.06 kg·m2；黏滞摩擦系数B= 0.001 kg·m2/s；磁极对数n=5。负载扰动转矩初始值为5 N·m。模糊自适应非奇异终端滑模控制器的参数选取为：β=200 ，p=7 ，q=5 ，λ=0.05 ，μ=0.05，K=30。系统采用离散化仿真方式，电流环频率为10 kHz，速度环和位置环频率为1 kHz。

模糊自适应非奇异终端滑模控制伺服系统的仿真模型，如图6 所示；搭建的SVPWM 算法仿真模型，如图7所示。

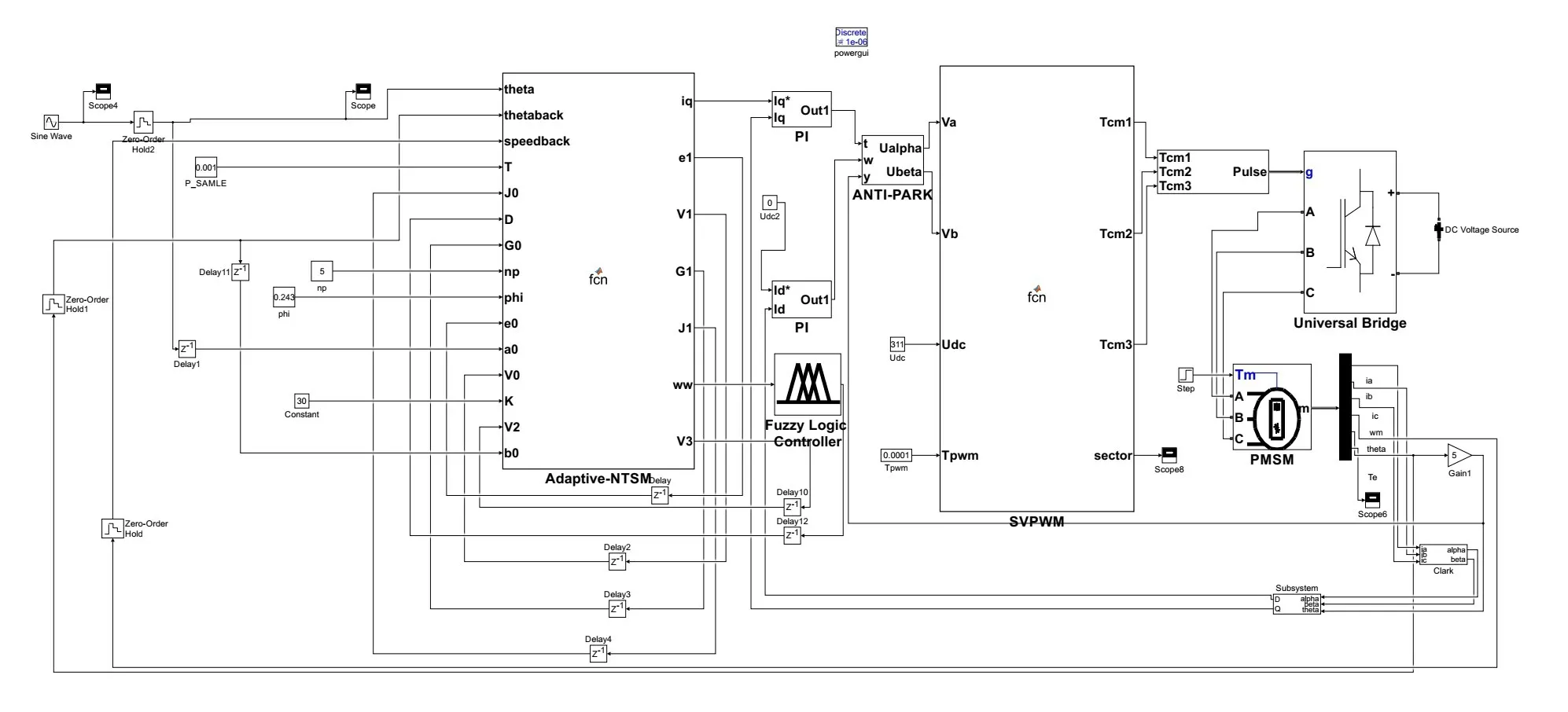
图6 模糊自适应NTSM伺服系统仿真模型Fig.6 Simulation model of the fuzzy adaptive NTSM servo system

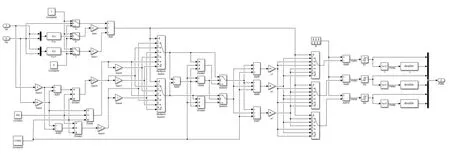
图7 SVPWM算法仿真模型Fig.7 Simulation model of the SVPWM algorithm

给定系统位置指令为0.5sinπt的正弦信号，要求伺服系统输出位置能快速精确跟踪位置指令，且对系统结构参数变化和扰动具有良好的鲁棒性，如图8 和图9所示。

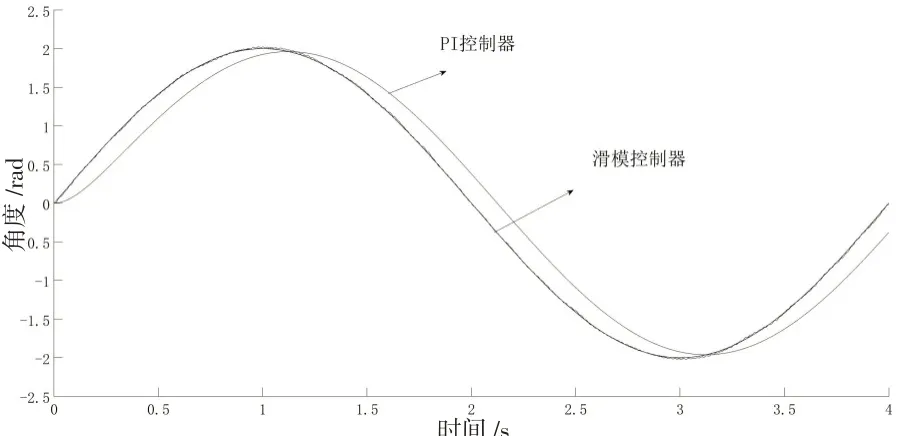
图8 系统跟踪曲线Fig.8 Position tracking curve

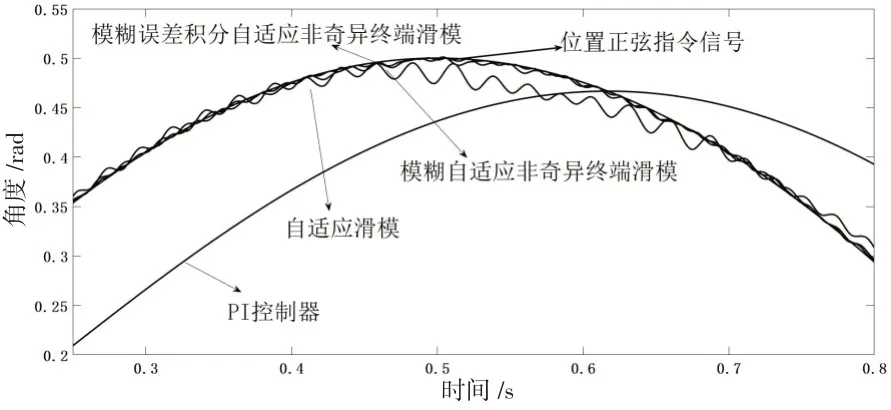
图9 跟踪曲线局部放大示意图Fig.9 Partial enlarged drawing of tracking curve

与传统的PID 控制器相比较，采用滑模控制的系统控制方式虽可以提高系统的响应速度并减小跟踪误差[15-18]，但传统的线性滑面收敛速度小于非奇异终端滑模面，且跟踪过程中，输出控制信号抖动较大，控制信号中这种抖动的存在正是由于控制律中符号函数的存在，这代表了对未知负载扰动的鲁棒性，倘若完全消除控制信号中的抖动则会使系统的鲁棒性变差，故只能采取减少抖动的方式来处理，如用模糊控制估计抖动上界的方法可以有效减少抖动问题。

为了进一步减小跟踪误差，将设计的误差积分非奇异终端滑模控制器与非奇异终端滑模控制器的输出误差绝对值做比较，如图10所示。

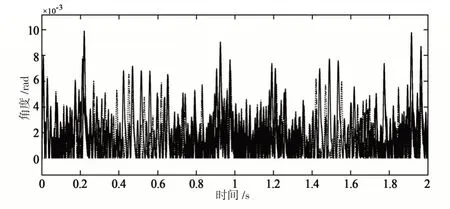
图10 误差绝对值比较图Fig.10 Error comparison diagram

从图中可以看出，利用误差积分的非奇异终端滑模控制器可明显减小跟踪过程中的误差，从而进一步提高了系统的跟踪精度。

为了验证模糊误差积分非奇异终端滑模控制器对系统结构参数和扰动变化的鲁棒性，设计系统在0.4 s 时刻，将电机末端的转动惯量变为0.028 kg·m2，负载扰动变为10 N·m，比较仿真结果与PID控制器仿真结果，如图11所示。

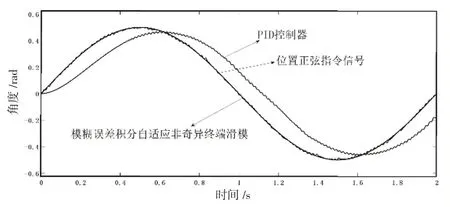
图11 参数变化后跟踪轨迹曲线Fig.11 Tracking curve after parameter change

从图中可以看出，在系统结构参数和扰动发生变化后，模糊误差积分非奇异终端滑模控制曲线抖动程度较小，跟随精度较高。而传统的PID 控制器在跟随过程中出现了明显的抖动，系统鲁棒能力不足。

6 结论

本文提出了1种基于误差积分的模糊非奇异终端滑模控制不确定永磁同步电机伺服系统控制方法，利用MATLAB/Simulink 建立了不确定永磁同步电机伺服系统在不同控制方法下的仿真模型，得到了不同控制方法下的伺服系统输出跟踪轨迹曲线。仿真结果表明，所提出的基于误差积分的模糊非奇异终端滑模控制方法对不确定伺服系统具有良好的鲁棒性，提高了系统的响应速度和跟踪精度。