以真情实景、客观存在为本落实数学应用教学——由正确答案不能得分引发的思考

张蕴禄 霍秋萍 (山东省实验中学东校 250109)

要问当下高中数学教学最流行的话题是什么，我们几乎会异口同声地说：“数学学科核心素养．”高中数学课堂刮起了数学学科核心素养的东风，高中数学教学要以发展学生学科核心素养为导向，新高考也将从能力立意转到素养导向．整个高中数学教学的方方面面仿佛都沉浸在核心素养的海洋之中，教师备课、上课、听课、评课、做课题研究、写文章等每一个环节只要少了“核心素养”就好像已经落伍了．然而在一次考试中有两个题目，学生的解答与现实生活实际完全吻合，只是由于与评分标准提供的“标准答案”不同而不能得分，这引发了笔者的关注和思考．很多根深蒂固的习惯性做法使数学应用变得举步维艰，甚至背离了方向．数学学科核心素养要真正落地生根，甚至开花结果，我们任重而道远．

1 没有得分的正确答案

例1有4张卡片，正反两面上分别标有1和2，3和4，5和6，7和8.选其中3张并排在一起组成三位数，不同的三位数有多少个？

例1是某次考试中的一个题目，评分标准提供的标准答案为下面的解法1．

解法1 完成这件事共分3个步骤：第一步，选择一个数放在首位上，有8种不同的选择；第二步，再从剩下的6个数中选一个数放在第二位上，有6种选择；第三步，再从剩下的2个数中选一个数放在第三位上，共有2种选择．于是可构成8×6×4=192个不同的三位数．

阅卷时发现，个别学生解答时用的是下面的解法2．

解法2 阿拉伯数字“6”倒过来可作“9”用．若不用卡片“5,6”，有6×4×2=48种.若用卡片“5,6”，这张卡片可提供5,6,9三个数字共3种情况，然后再选择一个位置放好共3种情况；还剩下2个位置、3张卡片，有6×4=24种.于是一共可组成不同的三位数有48+3×3×24=264个．

笔者认为解法2符合客观存在，应该得全分，课堂教学时也是这样处理的．可结果是由于解法2与标准答案不同而不能得分．无论笔者如何“申辩”，还是不能得到阅卷组长的认同．其理由是题目中没有注明“6”可作“9”用．考试以后学生纷纷质疑笔者，为什么不能得分、到底什么情况下“6”可作“9”用．笔者无奈，只能极不情愿地告诉学生，只有在题目有说明的情况下“6”方可作“9”用并能得分．同样的问题还发生在下面的例2．

例2对某种产品的6件不同的正品和4件不同的次品一一进行测试，直到区分出所有的次品为止，若所有次品恰好到第6次测试时被全部发现，则这样的测试方法有多少种可能？

例2也是该次考试中的一个题目，评分标准提供的标准答案为下面的解法1．

与例1类似，阅卷时有个别学生解答时用的是下面的解法2．

例2是各类教辅资料和网络上的一个常见问题，所提供的解法也多为解法1．与例1类似，解法2也是由于与标准答案不同而不能得分．这次阅卷组长拿出了一本教辅资料上的一道例题及其解法作为依据．

例3某产品有3只次品，7只正品，每次取出1只测试，取后不放回．求：

(1) 3只次品恰好到第5次全部被测出的概率；

(2) 3只次品恰好到第k次全部被测出的概率P(k)的最大值与最小值．

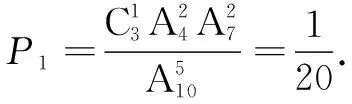
(3≤k≤10)．

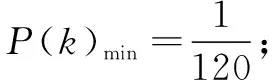
笔者认为例3的解法1是不妥当的，若第7次发现第3件次品，或者前7次发现的全部是正品(剩下的3只就是3件次品)，都应该叫3只次品恰好到第7次全部被测出；第8次发现第3只次品，或者说前8次中有一件次品，都属于3只次品恰好到第8次全部被测出；第9次发现第3只次品，或者说前9次中有2件次品，都属于3只次品恰好到第9次全部被测出；k的取值范围应为3≤k≤9．例3第(2)问的正确解法应为下面的解法2．

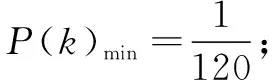
但无论笔者如何解释，阅卷组长还是没有同意，并且许多阅卷教师也提出了反对意见，甚至有部分教师认为包括例1在内笔者是在“强词夺理、钻牛角尖”．最终结果是例2采用解法2的学生被判零分．笔者认为例1、例2的解法2与现实生活实际完全吻合，在现实世界中也是“真实存在”的．这种正确解法不能得分使笔者陷入极端的困惑之中，并由此联想到了中国足协由于考虑不周而引发的几起“闹剧”．

2 中国足球史上的几起“闹剧”

许多球迷朋友知道，中国足协经常制定出漏洞百出、令人啼笑皆非的规则和政策．这些规则和政策使得各种“闹剧”时有发生，诸如“6,9风波”“洗牌门”“输球进中超”等．

1999年中乙决赛遭遇了排名难题，中国足协不得不从小组比赛并列第二名的毅腾连铁和绵阳丰谷中通过抽签决定其中一支队伍晋级八强．当时郎效农主任的具体做法是让两队代表分选“单”“双”，然后各从0至9的数字中抽出一数相加，如果和是单数，那么选“单”者获胜，如果和是双数，选“双”者获胜．结果在抽签当场选择单数的毅腾教练王军将纸条交给郎效农后，郎效农当场询问王军数字，王军答曰“9”．由于此时绵阳队总经理李海生目睹了整个问答过程，随即答道：“绵阳队也是9．”正是依靠这个似是而非的9(也可能是6)绵阳队晋级．事后毅腾连铁向足协提出了申诉，一时间两个阿拉伯数字“6”和“9”搞得足协焦头烂额．

2003年末代甲A，中国足协定下一个特殊的冲超规则，即捆绑式中超资格积分公式：中超资格积分=2002年的排名×0.5+2003年的排名．这个看似理想的计算方法，却差一点使“输球进中超”成为现实．因为按照这一特殊规则，最后一轮重庆队只有输给青岛队(无论输赢，重庆队都是2003年的倒数第二名)，在天津队输球的前提下就会通过提高青岛队的名次而挤掉天津队，重庆队若是赢球则彻底失去冲超希望．于是出现了震惊中国足坛、在世界足坛也是极为罕见的“输球保级战”闹剧．幸运的是最后一轮天津队赢了球保住了进入中超的资格，才避免了贻笑大方的结局发生．

2008年中国足协针对武汉光谷的退出制定了一个有巨大漏洞的规则：所有比赛都判武汉0∶3输，但这些比赛都算正常比赛．上海申花队很好地利用了这一规则漏洞，在与山东鲁能队的比赛中(下一轮申花要对阵已退出的武汉光谷，只要凑够4张黄牌，就可以在不用比赛的情况下消掉身上的黄牌)申花队一共主动申请到10张黄牌和1张红牌．这就是震惊中国足坛的申花队“洗牌门”事件．

事实上，中国足坛的每一起闹剧都是由中国足协考虑不周全、不细致、主观臆断，忽视了某些“客观存在”造成的．如果制定规则时把各种“客观存在”考虑得再缜密周全一些，类似闹剧是完全可以避免的．

3 由正确答案不能得分引发的思考

3.1 不要让历史的闹剧重演

笔者为何花费如此多的篇幅介绍中国足协由于考虑不周而犯的低级失误，一个重要原因就是这些闹剧的发生难道与我们的学校教育没有关系吗？另一个原因是难道我们还要让类似的闹剧再度上演吗？诚然，如果例2中提示“6可作9用”，许多学生就会考虑到这一点．同样的道理，如果当时有人给郎效农主任注明“6可作9用”，那郎主任还会犯如此低级的错误吗？如果题目中没有注明，学生却想到了，那才是难能可贵的．笔者相信这样的学生将来走向社会是不会犯“足协式错误”的，即便是抽阿拉伯数字也会把6与9单独作一下标记以示区别．现实生活中存款、贷款、打借条等我们习惯于用中国大写数字而非阿拉伯数字，一个主要原因就是阿拉伯数字容易被涂改．

笔者认为，例1的解法1是一个正常思维结果，答案是对的，但不能说好．解法2不仅是对的，而且比解法1要更好．若前者得满分10分的话，后者应得12分，因为这是有创造性的答案．按例3的解法1，要找出3件次品的实验次数k的取值范围为3≤k≤10．如果某人抽9次都不能找出所有次品，非要10件产品全部取出才能找出3件次品，我们只能说这个学生有点“二”，这样的学生踏入社会后很难说不会重复“足协式错误”．如果说例1的解法1可以说对而不能说好，例2的解法1就应该是一个错误的解答．学生用例1与例2解法2的方式思考问题，决不是钻牛角尖，而是思维的广阔性更强，考虑问题更缜密周全．

3.2 数学应用的本质是数学为社会实践服务

数学是刻画自然规律与社会规律的科学语言和有效工具．荷兰数学家弗赖登塔尔指出：“数学源于现实，就必须寓于现实，并且用于现实．”数学应用的本质是数学为社会实践服务，是用数学的眼光观察世界，用数学的语言表达世界，用数学的思维分析世界，而不是实际问题符合于数学模型(或者说让实际问题迁就数学模型)，这应该成为数学应用教学的立足点．当然，数学教学中让实际问题服务于我们的教学这是无可厚非的，但这不能背离了数学服务于社会实践的本质．也就是说数学应用教学是运用数学知识解决实际问题，应该以实际问题为中心，而不是以数学为中心、教学为中心．有了这样的立足点我们的数学建模与应用才能落到实处，才能不流于形式．

3.3 真情实景是编拟数学应用问题的基本原则

根据数学知识来编拟应用问题本无可厚非，因为在数学教学中数学的应用也不是盲目应用，而是根据所学数学知识有针对性地进行．但是数学应用问题必须是从实际中来，必须与实际问题相吻合，呈现给学生的应用问题必须是真情实景，而不是主观臆造．

文[1]提出了高考要以真情实景落实“五育并举”，而编拟数学问题必须突出真情实景．2019年高考文科、理科全国卷Ⅰ第4题以著名雕塑“断臂维纳斯”为例，探讨人体黄金分割之美．2019年高考文理、理科全国卷Ⅱ第16题，融入了中国金石文化，赋予几何体的真实背景．这些典型的应用问题都给人一种真情实景之感．

例41936年美国权威的《文学文摘》杂志社，为了预测总统候选人民主党罗斯福与共和党兰登两个谁能当选，以电话簿上的地址和俱乐部成员名单上的地址发出1 000万封信，收回回信200万封，花费了大量的人力物力．杂志社相信自己的调查结果——兰登将以57%对43%的比例获胜，并进行大力宣传，最后选举的结果却是罗斯福以62%对38%的巨大优势获胜连任总统．这个调查使《文学文摘》杂志社威信扫地，不久只得关门停刊．请问这家杂志社预测失败的原因是( )．

A．抽样的样本容量太小

B．收回回信比例太小

C．调查结果公布过早，结果公布后罗斯福团队扩大宣传实现逆袭

D．抽样具有片面性，没有保证每个选民被抽到的概率相等

例4以历史真实事件为背景，是真情实景的典型案例，解答时运用统计知识方法来分析．这是典型的用数学的思维来分析世界．

3.4 客观存在应成为应用问题的评判依据

考试应该有答案，也应该有评分标准，这是无可争议的．我们经常说要敢于向权威质疑，我们完全可以向命题人提供的“标准答案”质疑．另一方面，不同的人从不同的角度来思考可以得出不同的结论，这是极为正常的一件事情，为什么成千上万的学生都要和命题人从同一角度思考问题？特别是一些与现实生活密切相关的实际问题，从不同角度考虑往往会得出不同的答案．

例5一排共12个停车位置，今有8辆车需要停放，要求空位连在一起，则停车方法有．

在解答例5时，也出现了两种不同的解法：

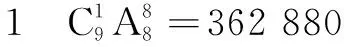
显然，解法1是把8辆车看做不同的车，解法2是把8辆车视作相同的车．笔者认为，从不同的角度都有其道理．若从停车场管理员的角度去考虑，往往管理员不考虑车的不同，不管这辆是“奥迪”、那辆是“大众”，他只关心哪个位置停了车，哪个位置还空着．从此角度分析，把所有的8辆车视作相同的车是完全合理的．若从另一角度去分析，例如你和朋友一行共8辆车需要停放在停车场，此时停车不仅要考虑哪几个位置停放，还要考虑哪个位置停放的是哪辆车，就应该把车视作不同的了．

例6如图1，要在河边修建一个水泵站，分别向张村、李庄送水，修在河边什么地方可使所用水管最短？

这是初中课本的一个传统、典型的应用题．很显然，这是根据对称点的性质编拟出来的，其答案就是图1中的点C．而有位学生提出:如果DA+AB

图1

据笔者了解，许多供水问题正是按照这位学生提出的供水方案来完成的．也就是说，课本提供的答案与实际情况是有出入的．不过学生在解答时若选择点D肯定是与答案不符的．

所以我们在处理有关数学应用问题时可能会出现多种“正确答案”并存的现象．如果我们被所谓的“标准答案”束缚着，在教学中充斥着不是“对”就是“错”，不管实际问题的实际背景，教条式地解读已知条件，这样的教育能培养出创造性人才吗？

求解数学应用问题离不开数学知识和方法，但判罚的依据应该是与实际问题的吻合程度，只要是存在的就应该是合理的．这应该成为广大数学教师在教学、阅卷等活动中共同遵守的一个基本原则．有了这样一个原则，阅卷时出现的许多棘手问题就有了一个判罚的依据；有了这样一个原则，我们面对学生诸如“什么时候能用”的疑问时，也就有了答疑解惑的依据．

4 结束语

数学教学应以真情实景、客观存在为本落实数学的应用，让数学真正为社会实践服务．如果我们无视客观存在，唯数学论，将来还会出现新的意想不到的闹剧．到那时再来反思我们的教学、反思我们的学校教育是不是已经晚矣．