基于热管技术的PRS水池自然对流传热特性分析
2022-11-15陶汉中李艳南
乔 珂,陶汉中,李艳南
(南京工业大学 能源科学与工程学院,江苏 南京 211816)
0 引 言
华龙一号(HPR1000)作为中国自主研发的第三代压水堆核电站,在设计上结合了主动冷却与被动冷却概念[1]。 二次侧被动余热排出系统(PRS)是HPR1000 被动安全冷却系统的重要组成部分,在核反应堆系统发生冷却剂损失事故(LOCA)和非冷却剂损失事故时,通过热交换器将二次侧的蒸汽的热量导入外部水池中。 然而该系统使用时间超过72 小时必须要进行及时补水[2],否则系统将因冷却水蒸发消耗而导致被动冷却系统的功能受到严重损害。
分离式热管换热器具有传热效率高、系统结构简单、布局方便等优点,广泛应用于航空航天、电子、化工、冶金等领域[3]。 目前,大型分离式热管应用于PRS 水池的设计研究较少,可参考其应用于乏燃料池的设计研究。 文献[4,5]设计了基于分离式热管的乏燃料池被动冷却系统,在发生事故后通过环境空气的自然对流去除池中乏燃料的衰变热。 文献[6,7]设计了大量的实验来研究分离式热管的性能,并证明应用分离式热管来实现乏燃料池的被动冷却是可行的。 文献[8 -10]对应用分离式热管的乏燃料水池进行了数值研究,分别获得池内的温度场于流场特性、最佳传热模型以及冷凝段最佳的布置方式。 然而,这些先前发表的论文很少研究将分离式热管应用于PRS水池的长期运行,从而延长被动安全时间。 本文在结合现有相关研究成果的基础上, 针对HPR1000 提出了一种基于热管技术的PRS 水池长期冷却方案,并通过前人的经验公式验证了数值方法的准确性,研究了72 小时内采用分离式热管的PRS 水池的自然对流特性、管束的瞬态传热特性以及布置方式的影响。
1 设计方案
本研究中设计方案见图1,该方案由位于安全壳外部水池、热交换器、分离式热管换热器以及安全壳内部的应急补水箱组成。
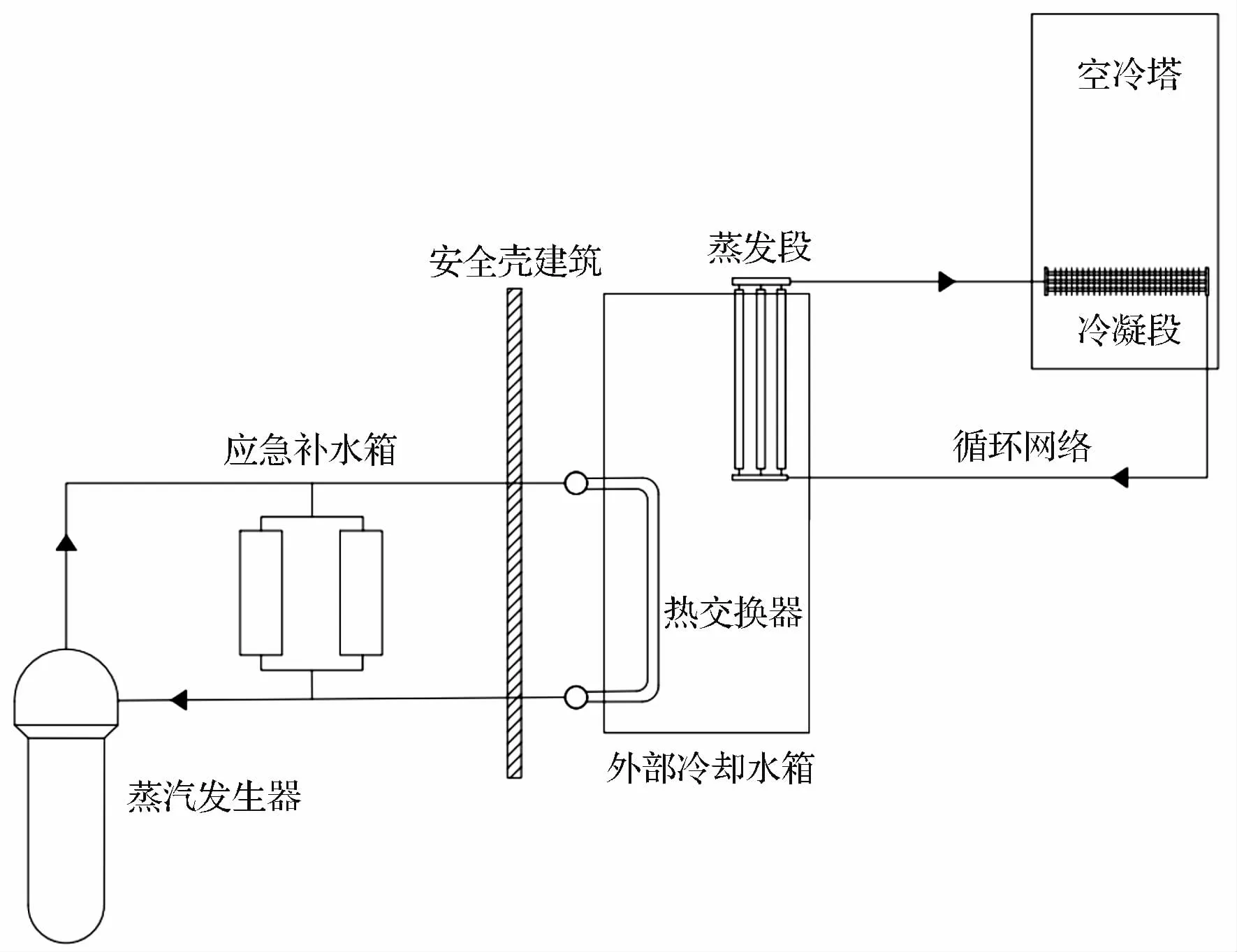
图1 设计方案示意图
在全厂断电或主动冷却失效事故中,PRS 被触发,二次侧蒸汽发生器(SG)产生的蒸汽通过PRS 换热器将热量释放到水箱内的水中。 随着池水升温,分离式热管换热器启动,热量由蒸发段传递给位于厂房外部的冷凝段,最终以空冷的方式向外界散热。 通过热管换热器冷却后的冷凝水流回SG。 根据设计方案,在水池中分为8 排共布置51 组分离式热管换热器。 每组分离式热管中蒸发端由8 根长度为6 m,管径为70 mm,管间距为100 mm×130 mm的光管组成;冷凝段由40 根长度为2 m,管径为70 mm,叉排布置的翅片管组成。 分离式热管蒸发段作为系统冷源,池内换热器作为热源。 该系统中的自然对流循环能够长期维持反应堆安全的状态,时间不局限于72 小时。
2 分离式热管简化
本文中热阻网络模型见图2,热阻网络模型是预测热管传热能力的常用办法,各部分热阻的具体计算公式可以参阅文献[11],分离式热管可以假设由多根热管并联组成,认为每根热管的导热系数是相同的,分离式热管的总热阻与等效热导率可以由下式得到:
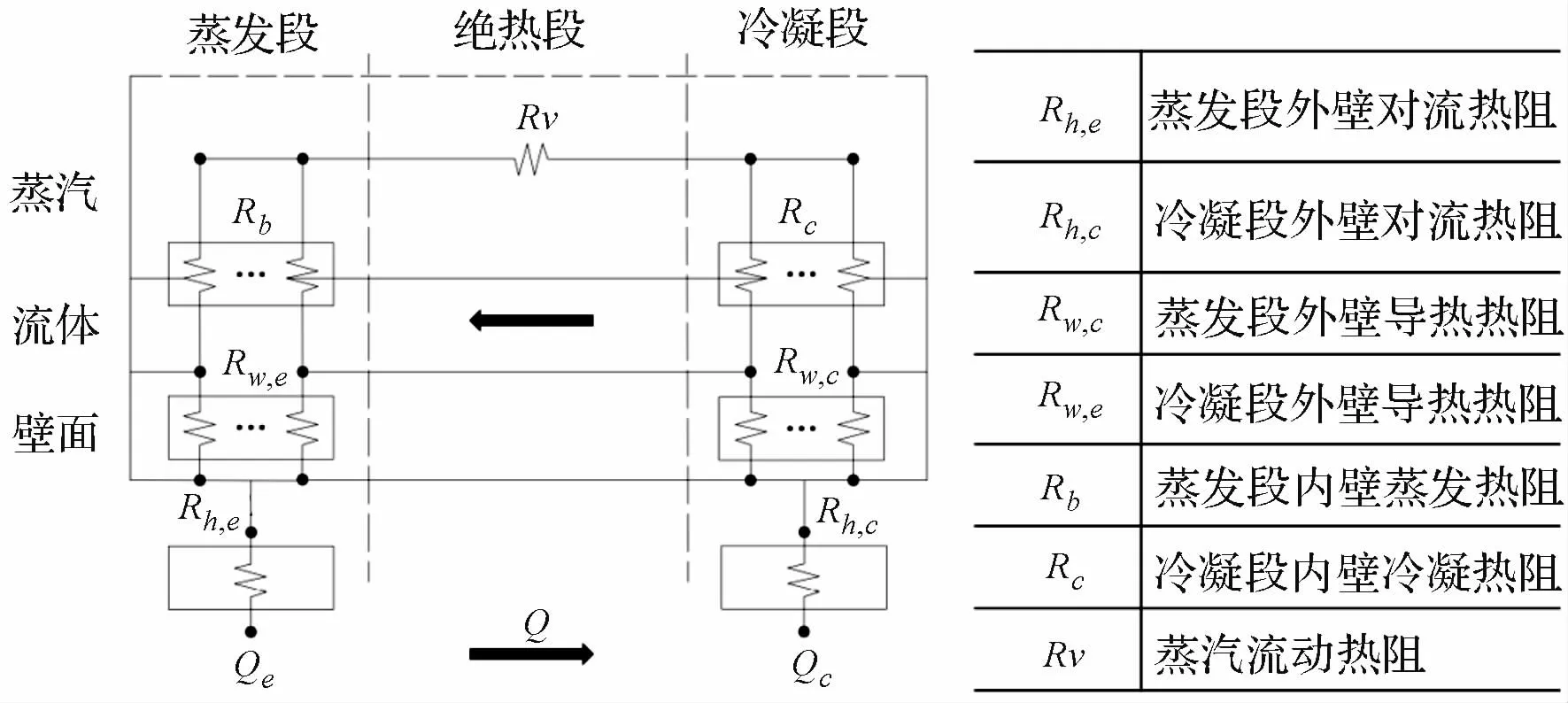
图2 热阻网络模型
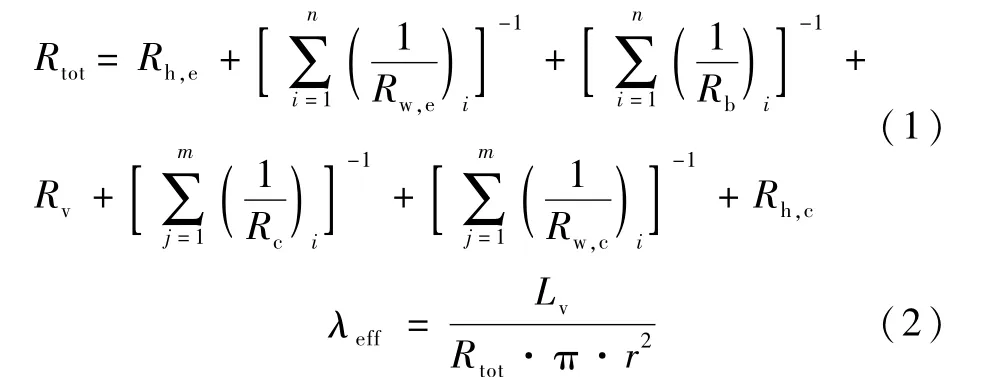
式中:Rtot是单独热管的总热阻;r是管束半径;Lv与分离式热管中的蒸汽路径(m)有关;λeff是等效热导率,它将作为边界条件计算。通过计算得出,设计方案中分离式热管的等效热阻为0.705 ×10-3K/W。
3 数值仿真分析
3.1 几何模型
HPR1000 中PRS 系统与PCS 系统均分为三个相同的序列,每个序列共用一个T型水箱,而在本设计中,热管的蒸发段仅布置在PRS 换热器所处的中间区域,为了强化中间水域的流动与热管区域的传热,将T型水箱的两侧分别设置挡板,因此PRS 系统的外部水箱可以近似为的矩形水箱。 几何模型如图3 所示,由于整体仿真研究将消耗巨大的计算资源,因此在仿真中将分离式热管的冷凝段简化为恒温截面,蒸发段简化为具有相同长度的圆管。 由于PRS 换热器结构复杂,因此将其简化为体热源(体积为73.15 m3),均匀布置在水箱下部。 整个水箱的流场有相似之处,可以利用中心的一组对称模块进行数值分析。 管束的三种布置方式及尺寸见图4。
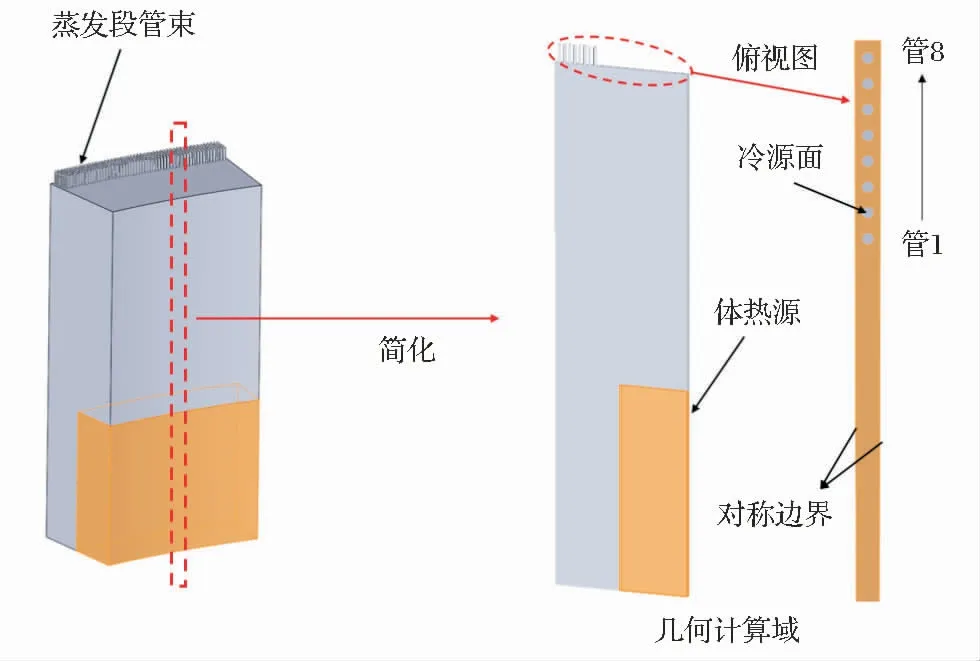
图3 几何模型
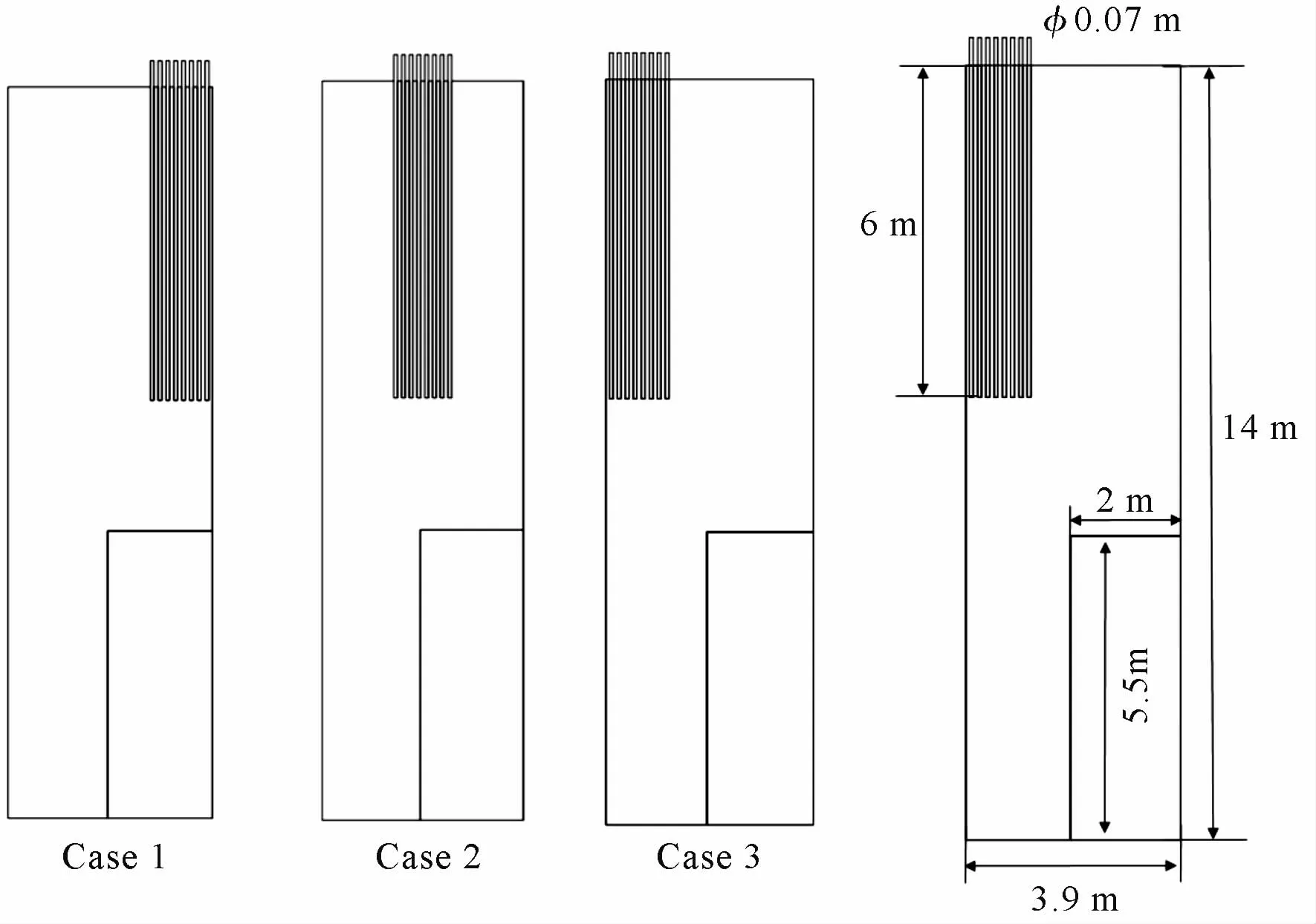
图4 三种布置方式及模型尺寸
3.2 物理模型
模型假设如下:
(1)忽略水的蒸发,只考虑单相流,流体物性为温度相关的拟合函数如表1 所示。
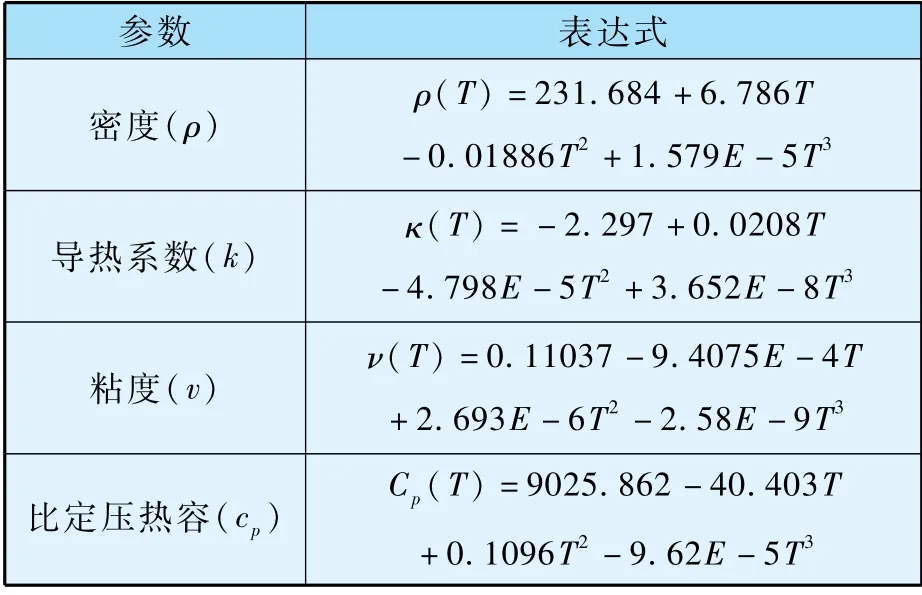
表1 流体的物性参数
(2)水池壁面绝热,忽略热辐射的影响。
(3)假设所有蒸发管的热导率相同。
(4)将分离式热管的冷凝段简化为恒温的圆形截面。
基于上述假设,控制方程如下:
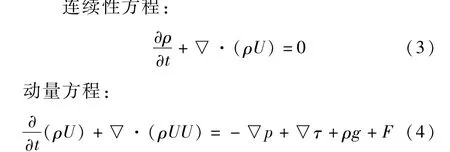
能量方程:
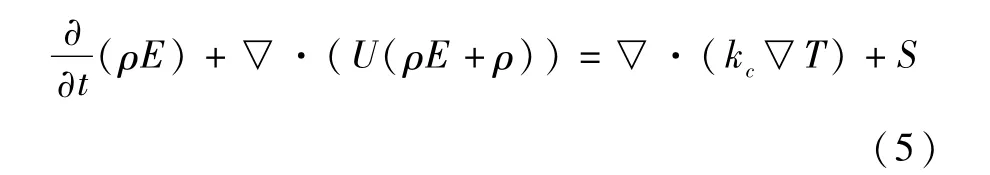
式中:ρ为密度;t为时间;U为空间速度矢量;τ为粘性剪切应力;ρg +F为体积力项;kc=k/cp,k为流体的传热系数,cp为流体比定压热容,S 为粘性耗散项。
3.3 边界条件与数值方法
本研究基于CFD软件对设计方案进行瞬态仿真,采用SIMPLE算法求解,压力方程和能量方程分别选用体力加权法与二阶迎风进行离散化。对于残差的收敛标准,能量守恒方程为10-6,其他方程为10-4。 数值计算中选择RNG k-ε湍流模型,考虑浮升力效应,近壁面效应采用增强壁面热效应函数。 边界条件中,假设冷源截面温度与水池初始温度均为60 ℃,体热源功率为15 MW(反应堆热功率的0.5%),水池两侧设置为对称边界条件,其他壁面为无滑移的绝热壁面。 通过热阻网络计算,蒸发管的热导率为λhp=38.7 ×105W/m。
3.4 数据处理
基于蒸发管长度(L)的Ra 数可以由下式计算:
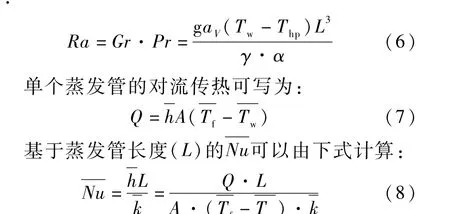
式中:A为单个蒸发管对流换热面积;Tw为蒸发管局部温度;Tf为蒸发管附近流体温度;L 为蒸发管长度;流体导热系数k通过定性温度定义。
在池中高度方向上均匀取15 个数据面,沿高度方向的平均温度梯度由下式计算:
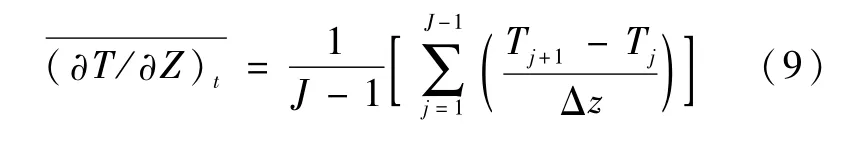
式中:J取15;T为每个面的加权平均温度;Δz为两个数据面之间的距离。
3.4 敏感性分析及模型验证
网格独立性验证是为了确保后续的数值结果不受网格影响,满足计算精度要求。 在数值模拟中创建非结构化网格,对蒸发管附近流体采用5层边界层来提高网格精度,并对热源附近的网格进行细化。 在网格独立性验证中,以热源功率为5 MW 时工况为例,网格方案在250 万到450 万之间变化,以平均水速、最大水速、平均水温和最大水温作为评价标准。 网格独立性检验结果如表2所示,当网格数达到400 万时,平均水流速度、最大水流速度、平均水温和最大水温的变化率小于0.5%,可以认为网格数量已经达到了足够的精度。
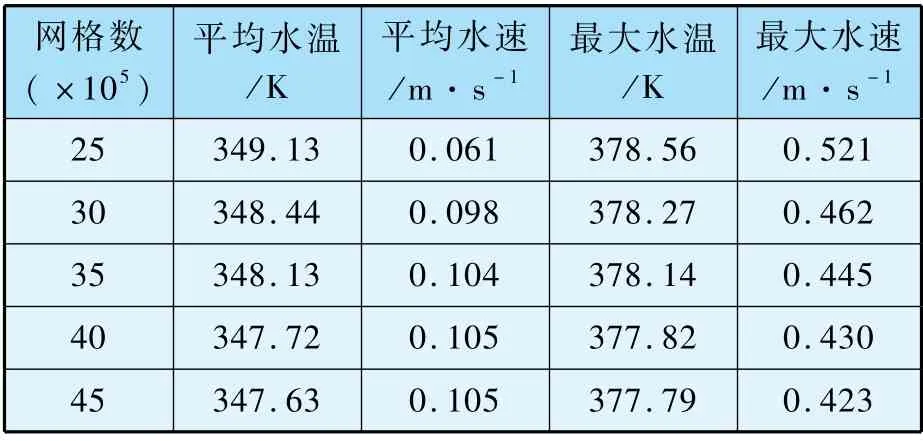
表2 网格独立性检验结果
此外,在时间步长敏感性分析中,以400 万网格数的方案为基础,分别对了五种时间步长方案(200 s、250 s、300 s、350 s、400 s)进行对比,结果发现,当时间步长小于300 s时,蒸发管的平均Nu数变化小于1%。 因此选择400 万网格作为后续研究的网格方案,300 s/步为瞬态分析时间步长。图5 显示了数值计算中蒸发管的Nu数随Ra 数的变化与前人实验关联式的比较,最大误差分别为8.8%、8.0%,进一步证明当前的计算在湍流条件下是相当准确的。
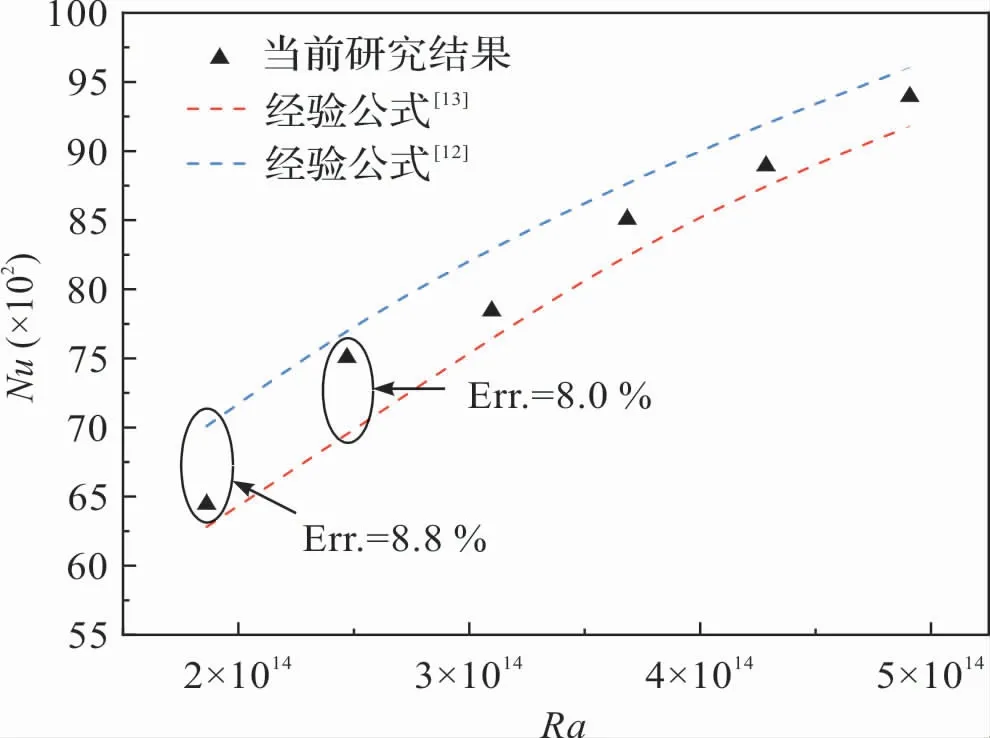
图5 当前研究与实验相关性之间的比较
4 结果与讨论
4.1 水池内自然对流瞬态特性
图6 给出了水池内温度场随时间的变化,可以发现,热源与热管蒸发管分别作为加热与冷却区域,在浮升力的作用下分别形成了上升羽流与下降羽流。 在加热初期,水池整体温度较低,蒸发管的冷却能力较低,水池内的传热主要以热传导为主,等温线趋于平直。 随着加热持续,池水温度逐渐上升,热源与蒸发管之间建立的自然循环增强,温度等值线发生弯曲。 热流体开始向水箱上部积聚,并蒸发管区域扩散,冷却后的流体再次回到水箱下部。 在t=10 ~20 h,热源附近流体的温度梯度逐渐增大,并热源上部形成局部“高温区”。 在加热的后期,水箱轴向热分层更加稳定,上升羽流与流体之间温差减小,其驱动力减小,水池内的自然循环逐渐达到稳定状态。
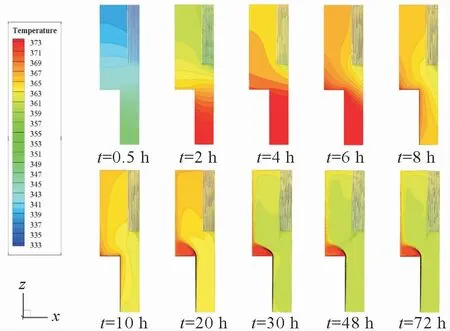
图6 水池内温度场随着时间的变化
水池在72 小时内的平均温度与沿高度方向上平均温度梯度的变化如图7 所示,可以发现水池内的自然对流可以分为三个过程:升温区(0 ~4.5 h)、变温区(4.5 ~32 h)、稳定区(32 ~72 h)。 在被动冷却系统启动阶段初期,水池下层的温度随时间逐渐上升,平均温度梯度快速增大,水池的平均温度出现一个突增的过程,在t=4.5 h 时,平均温度与平均温度梯度达到峰值。 在变温区中,蒸发管的启动使得水池中形成了自然循环,平均温度梯度逐渐减小,热分层逐渐转变为上层水温高于下层,平均水温在30 h 左右进入稳定阶段,水池内的平均温度梯度也不再发生变化。 蒸发管的冷却作用,对于温度场的调节发挥着重要作用,在瞬态过程中,水池内最大平均水温为369.16 K,达到准稳态时平均水温为361.67 K, 最大温差为7.5 K。

图7 平均温度梯度与平均水温随着时间的变化
4.2 管束传热能力瞬态特性
图8 给出了蒸发管传热量随时间的变化,从中可以发现,首排管束的传热量在换热初期出现突升过程,在2.5 h 达到峰值,其最大传热量与稳定时相差了51.2%。 表明首排蒸发管在换热初期可能会出现较短时间的传热峰值,这是因为随着水温的升高,首排蒸发管先接触到热流体,蒸发管壁温与传热量随之快速上升。 此外,在水池内自然循环尚未形成时,首排蒸发管发挥了阻碍作用,拉大了管束的传热量差距。 其余蒸发管的传热量在t=25 h 前后换热规律有所不同,这是由于水池内自然循环使得管束附近的流动状态发生转变。 当达到准稳态时,管束传热量随着排数逐渐减弱,最大传热差距为27.8%。
4.3 布置方式的影响
图9 对比了三种布置方式(Case1,Case2,Case3)下水池内平均温度的变化规律,可以看出,水池内平均温度均出现先升高后降低的趋势。 Case1 中水池的平均温度存在较大的波动,Case2 的水池温度在一段时间内明显低于其他两种方案。 在三种布置下水温峰值均在369 K左右,与稳定时的差值分别为3.5 K(Case1)、6.9 K(Case2)、7.5 K(Case3),可见Case3 中稳定时平均水温最低。 随着时间进行,Case3 的平均水温最低且最先进入稳定状态,Case1 的平均水温最迟达到稳定。 可见采用Case3 的布置方式可以加快水池内的温度场的稳定,耗时明显低于其他两种方案。
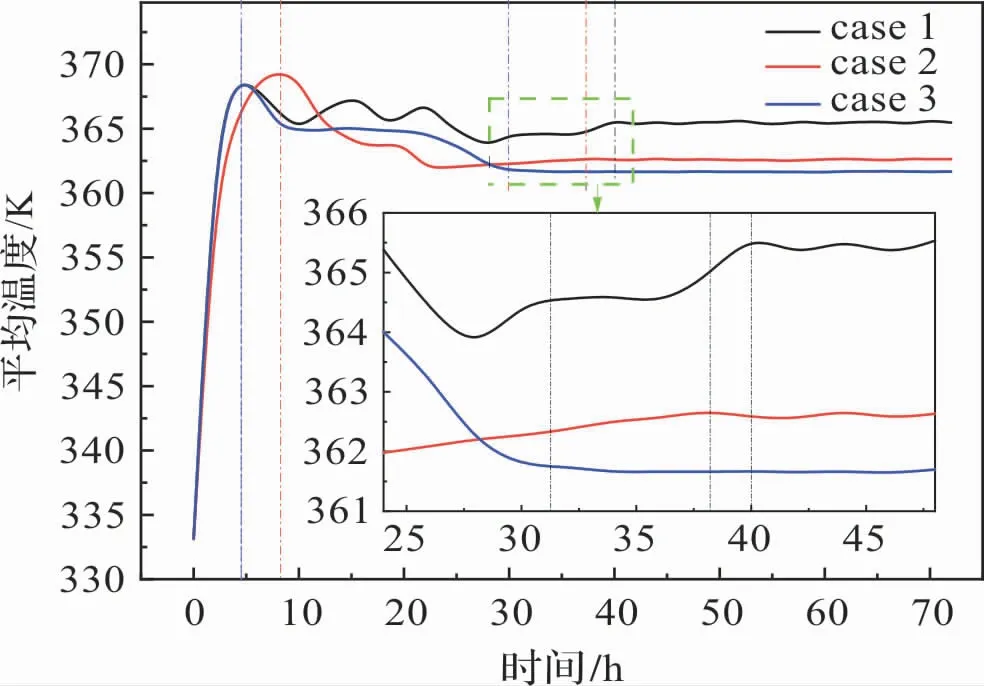
图9 不同布置下水池平均温度的瞬态变化
如图10 所示,三种布置方式下水池内的温度梯度都出现了先降低后升高的趋势。 在启动初期,Case3 中的平均温度梯度最低,热分层最小。随着水池内自然循环的形成,Case3 中的平均温度梯度变化速率大于Case2,且最先达到稳定的状态,Case1 中平均温度梯度处在着较大的波动,波动值保持在-0.7 上下。 研究发现,采用Case3的布置方式可以使水池内的温度场较快的进入稳定状态,Case1 中温度场始终处于不利于蒸发管传热的状态。
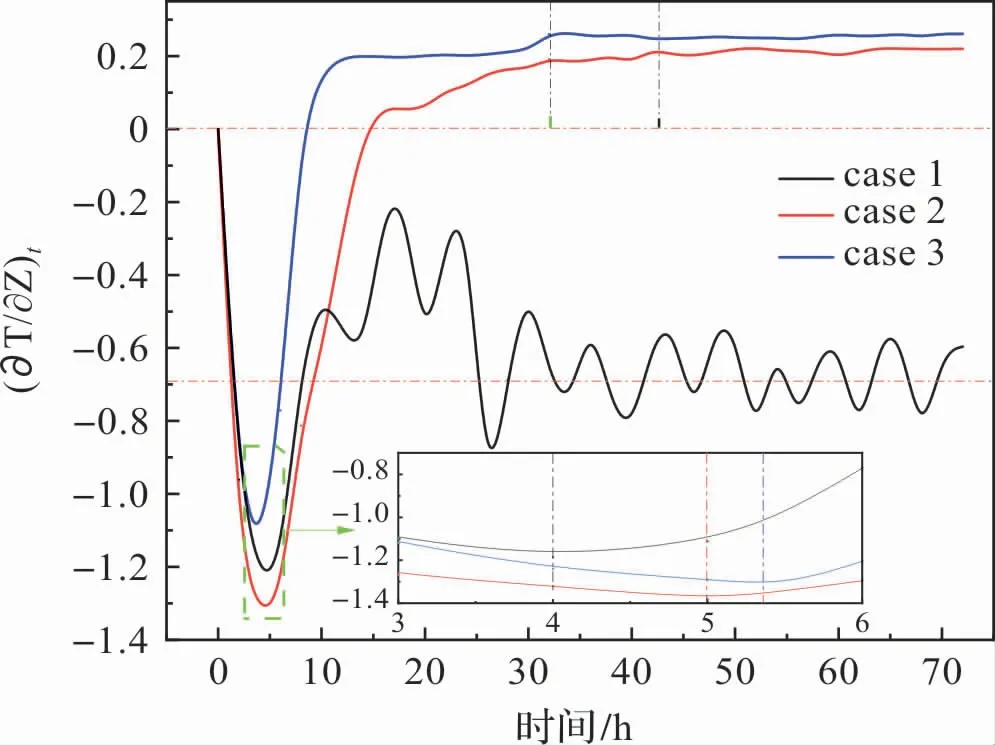
图10 不同布置下水池平均温度梯度的瞬态变化
当水箱内的自然对流达到准稳态时,蒸发管的传热量也趋于稳定。 图11 给出了三种布置方式下蒸发管的平均Nu 数的对比,可以发现Case1中蒸发管的传热能力逐排增大,Case2 与Case3 中则逐排降低。 三种布置方式下蒸发管之间的最大传热量分别相差41.1%(Case1)、56.9%(Case2)、27.8%(Case3)。 此外,Case3 中蒸发管总传热能力最大,相比于另外两种布置方式分别提高了9.7%(Case1)、6.73%(Case2)。 由此可见,当管束布置采用Case3 布置传热效果最佳且传热量差异性最小。
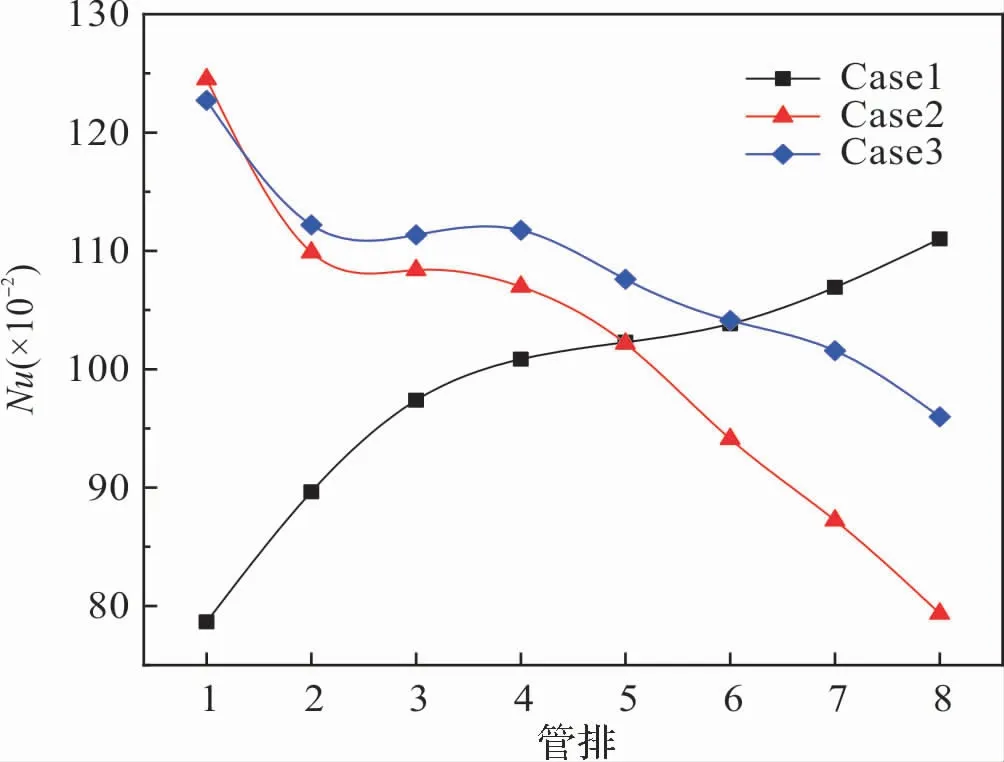
图11 不同布置下蒸发管的平均Nu 数对比
5 总 结
(1)在蒸发管的冷却作用下,PRS 水池内会逐形成自然对流循环。 在启动初期,水池内的热分层会出现短暂的峰值,平均水温与稳定时相差了7.5 K。 稳定后该非能动冷却系统可成功带走池内衰变热并使池内平均温度维持在361.67 K。
(2)水池内自然循环的形成使得管束附近的流动状态发生转变。 首排蒸发管在启动初期可能会出现较短时间的传热峰值,其最大传热功率与稳定功率相差了51.2%。 达到准稳态后管束传热量逐排减弱,最大传热量差距为27.8%。
(3)三种布置方式下,Case3 最先达到稳定且蒸发管之间的传热差距最小,其蒸发管总传热功率相比于另外两种布置方式(Case1、Case2)分别提高了9.7%、6.73%。
致谢:该工作得到了南京工业大学高性能计算中心的支持与帮助。
