动力配煤下入炉煤质参数快速计算分析
2022-11-15陈玲红蒋旭光吴学成岑可法
陶 翔,陈玲红,蒋旭光,吴学成,岑可法
(浙江大学 能源清洁利用国家重点实验室,浙江 杭州 310027)
0 引 言
入炉煤特性对电厂锅炉安全经济环保运行有着十分重要的意义[1],能否实时获取入炉煤质参数是指导锅炉运行的关键。 由于煤质在线分析设备成本投入较高的原因,目前电厂普遍未能实现入炉煤实时在线检测[2,3],大都采用离线采样化验的方式获取入炉煤参数,该方法存在时间严重滞后的问题。 近十几年,基于数据建模和机器学习的在线煤质软测量技术得到广泛研究和应用[2,3]。
电厂燃用煤种多样化,需要掺配不同煤种成为电厂普遍面临的问题,而入炉煤质受到动力配煤的影响。 我国开展了大量关于配煤掺烧的理论和试验研究,包括混煤参数计算、配煤优化和专家系统开发等[4-6]。 针对单煤和混煤的煤质特性、燃烧特性和污染物排放特性,通过试验研究,给出了混煤的各指标参数与组成单煤之间具有复杂的非线性关系的这一结论,而采用神经网络等机器学习方法可以获得比线性模型更准确的结果[7-9]。
浙江大学热能工程研究所是我国较早进行配煤研究的单位,提出了完整的动力配煤模型[10-12]。该模型需要一定的混煤掺烧试验数据和锅炉运行数据作为支撑,实际应用中可根据需求考虑约束条件。 配煤目标根据实际情况可分为三种:追求成本最低、追求优质煤种配比最小、追求劣质煤种配比最大[13]。 配煤优化算法方面主要包括神经网络[14,15]、遗传算法[16,17]、模拟退火算法、粒子群算法、布谷鸟算法[18]等。
某电站煤场共八个区域用于存放不同矿点煤质,担负向6 台锅炉机组供煤的生产任务。 6 台锅炉分三期建设,整体的燃烧性能存在较大不同,煤场配煤应满足锅炉对燃煤煤质特性的不同需求,特别是针对运行时间长、容易结焦、炉膛污染物排放严重的锅炉,需要掺配出准确的混煤以满足正常生产需要。
煤场配煤依据人工经验,将高硫煤与低硫煤、高热值煤与低热值煤简单进行掺混,考虑单一指标,没有准确的掺配指导,缺乏理论依据和数据支撑,容易造成混煤煤质不符合锅炉燃烧的需求。
此外,电厂入炉煤经采样化验到公布结果,存在较长的时间滞后,待公布化验结果,该煤早已入炉燃烧完毕,无法有效指导锅炉燃烧。
本文基于构建适用于锅炉运行实际的配煤掺烧模型和混煤煤质计算方法,系统溯源来煤入厂至入炉燃烧的全环节信息数据,快速计算获取入炉煤煤质参数。
1 分析方法
1.1 聚类分析方法
聚类分析依据对象的相似性对其进行分类,是一种无监督式学习的算法。 k均值聚类(kmeans clustering)算法是典型的基于距离划分的聚类分析方法。 聚类的目标是将数据集按照同簇数据距离尽可能小、不同簇数据距离尽可能大的原则进行划分。 假设簇划分为(C1,C2,…,Ck),则算法目标是最小化误差E:
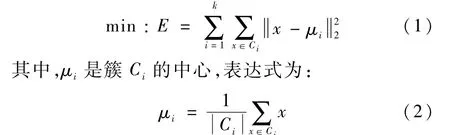
k-均值聚类算法具体过程如下:
(1)确定需要划分的簇数k值,采用k-means算法确定k个初始聚类中心点;
(2)计算所有数据点到各个中心点的距离;
(3)将每个数据点分配到距离最近的中心点所属的类别;
(4)计算每类数据点的平均值以获得k个新的中心点位置;
(5)重复步骤(2)到(4),直到聚类中心点不再发生改变。
1.2 配煤掺烧计算模型
1.2.1 混煤煤质计算
配煤模型研究的核心是对混煤煤质的确定,对于混煤煤质指标是否具备可加性存在较大争议。 陈文敏等[19]研究动力配煤主要煤质指标可加性,指出挥发分、发热量、硫分等煤质指标具有可加性,而由于水分经常变动,认为混煤水分不宜用可加性计算。 此外,陈怀珍[20]指出组成混煤的单煤配比必须明确是在什么基准下的配比,因为只有单煤煤质指标和配煤量比例都处于同一基准下,才能使用常规的加权平均法。 可见,即便煤质参数指标具备可加性,仍然需要在理论计算值的基础上进行修正。
若煤场两路供煤,从两个供煤区域取两种不同的单煤,编号i为1、2。 两种煤的煤量为B1和B2,假定两种煤充分混合,以单煤的空气干燥基为基准进行配煤。
由于煤量B1、B2是以空干基为基准的配比,因此可以直接使用煤量加权平均值计算混煤的空干基成分,如式(3)所示。
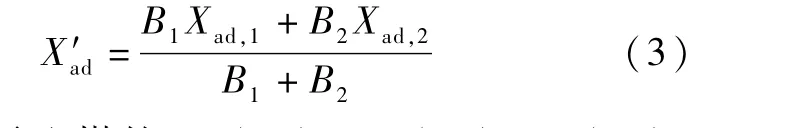
式中,X′ad表示配煤的Sad(%)、Mad(%)、Aad(%)、Vad(%)、或Qnet.ad(MJ/kg)加权值;Xad,1、Xad,2表示甲、乙两种单煤对应的空干基煤质参数;B1、B2表示甲、乙两种煤的空干基配煤质量,t。

除了直接使用式(4),也可以先使用式(3) 计算出混煤的Vad、Mad和Aad值。而混煤同样是一种煤,满足煤的不同基准之间的换算公式,故有:
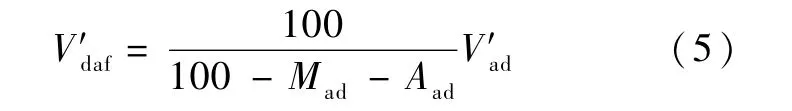
使用式(3) 和式(5) 计算的结果和式(4) 相同。

表1 列出了以空气干燥水分基准配比时,其他基准配比的换算系数。
为判断实际混煤煤质是否具备可加性,需对混煤的试验值与加权值之间的误差作出分析,可采用数理统计中的t检验法,判断煤质指标参数计算值与实测值出现的误差属于试验误差还是显著性差异。
以煤质实测值与加权值之间的差值作为样本,构建样本误差矩阵:
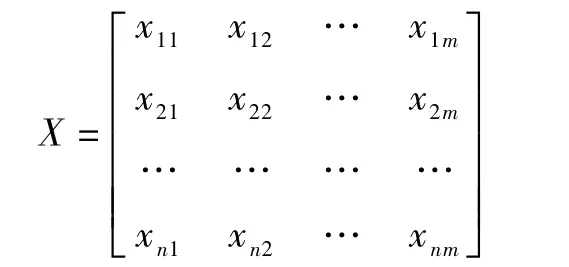
样本矩阵中m表示煤质指标个数,n 表示样本数。
如果某煤质指标具有线性可加性,那么实测值与加权平均值之间的误差服从正态分布ξ~N(μ,σ2),其中σ2未知,μ=0。 有,
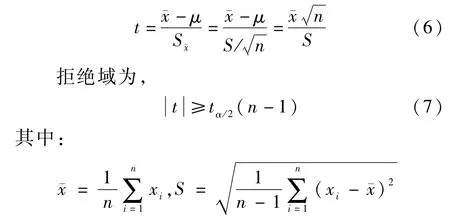
式中,ˉx为样本均值;S 为样本标准差;α为检验的显著性水平。
1.2.2 配煤掺烧模型
混煤掺烧是通过将两种或多种不同的单煤以一定的比例进行掺配,使掺配后的混煤特性达到锅炉燃烧和污染物排放的要求。
依据锅炉对具体煤质的要求和重要性排序,赋予不同权重,如表2 所示。
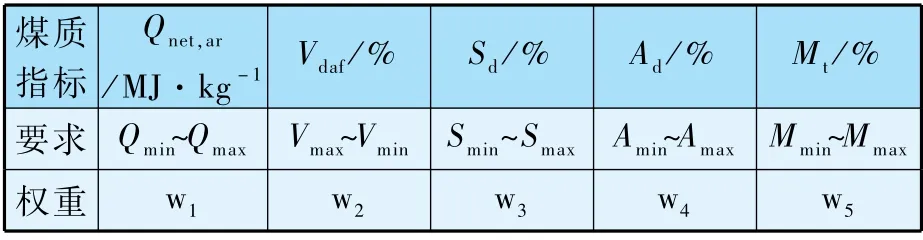
表2 煤质参数权重和要求范围
依据各煤质参数的要求范围,给出如下配煤掺烧模型:

上述计算模型可依据不同的配煤目标,输出不同的掺配方案,包括混煤煤种和配比。
1.3 入炉煤质获取计算模型
为提高入炉煤获取的时效性,梳理从入厂来煤到入炉煤采样的全环节和全数据流,图1 示出了整个详细过程。
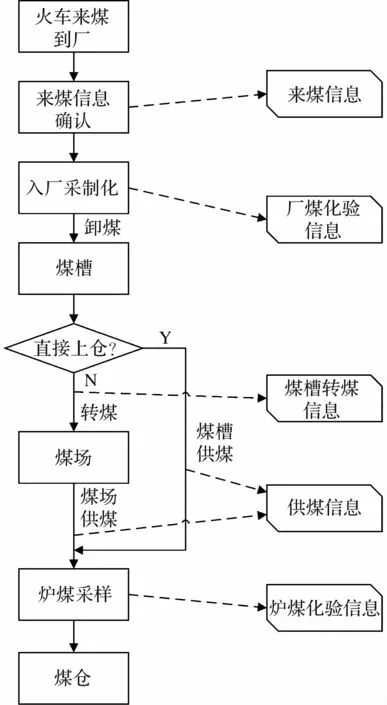
图1 煤场火车来煤到供煤全环节和信息流
煤场是两条皮带双路供煤,以表3 为例,说明供煤信息提供的数据内容。
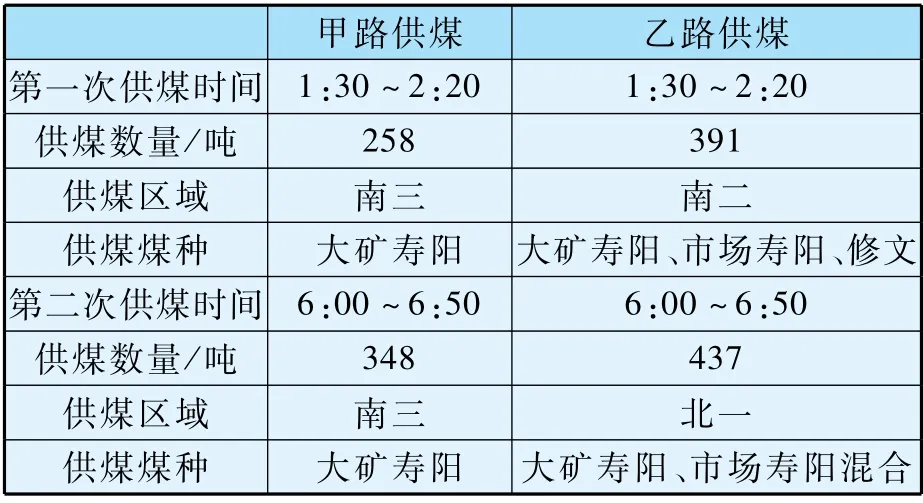
表3 班次供煤信息
为确定皮带入炉煤参数,即供煤煤质参数,有如下思路:
依据供煤信息的供煤区域和供煤煤种,追溯从煤槽转煤到煤场的该区域的该煤种数据,即确定了煤槽转煤信息,依据煤槽转煤时间和转煤煤种,匹配更早的火车来煤信息。 即确定了某时刻供煤对应的火车来煤信息,进一步依据火车来煤信息查询到入厂煤的化验数据信息,最终确定供煤煤质信息,打通入厂煤化验数据与入炉煤煤质之间的数据隔阂。
供煤信息溯源到入厂煤的化验数据信息,整个流程为图1 所示流程的逆向流程。 而电厂入炉煤的化验数据可以用于验证上述流程所得到的入炉煤参数。
上述思路的关键在于如何根据表3 的供煤信息去逆向推定煤场该区域的煤种何时从煤槽转入的,然后再确定煤槽的煤是何批次火车来煤,进而去查找入厂煤化验数据。 存在以下难点:
(1)由煤种名称无法确定煤质准确信息,同样名称的煤种特性变化较大,根据转煤煤种难以确定来煤批次;
(2)火车卸煤到煤槽,会与煤槽存煤发生混合;
(3)煤场情况混乱,整个煤场分区不够精细。
针对上述难点,提出如下假设:
(1)从煤槽转入煤场的煤可以在几天内快速用完,即供煤区域的某个煤种即为上次从煤槽转入到该区域的煤种,不包含更久之前的剩余煤;
(2)煤车来煤卸到煤槽,与煤槽存煤不发生混合,煤槽转出的煤种和煤量按煤车来煤先后循序依次转出。
2 分析与讨论
2.1 入厂煤质聚类分析结果
电厂来煤存在多个煤种,煤质参数分布较广,使用k均值聚类算法对入厂煤的低位发热量Qnet,ar、挥发分Vdaf、硫分Sd、灰分Ad和全水分Mt进行聚类处理。 以低位发热量为例,图2 示出了其聚类分析的结果(k=4)。 从中可以看出煤质的集中分布情况及其典型数值。
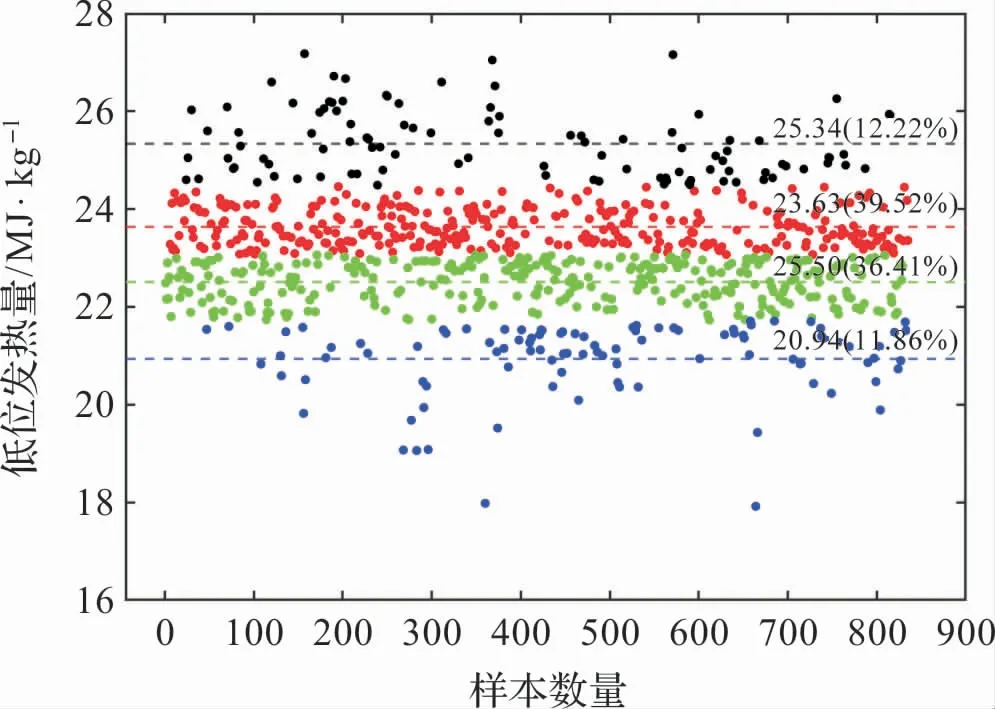
图2 低位发热量聚类分析结果
表4 是五个煤质指标聚类中心和占比情况,按占比大小来看,入厂煤发热量Qnet,ar的典型数值为22.50 MJ/kg和23.63 MJ/kg;Vdaf的典型结果为14.47%和15.78%;Sd典型数值为0.36%和0.89%;Ad典型数值为25.54%和28.92%;Mt典型结果为5.27%、6.62%和8.11%。 入厂煤参数为配煤掺烧研究和入炉煤特性计算提供数据基础。
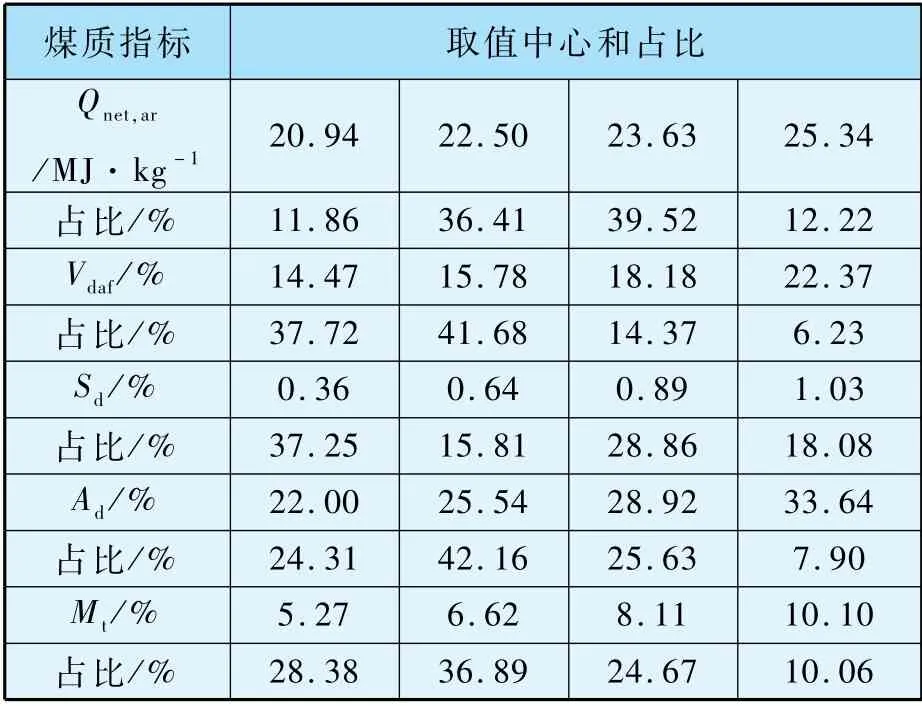
表4 入厂煤质聚类分析结果
2.2 混煤煤质确定方法
依据t检验方法,对30 组混煤的发热量Qnet,ar、挥发分Vdaf、硫分Sad、灰分Aad和水分Mt的实测值和加权平均值进行比较,混煤煤质指标统计结果如表5 所示。
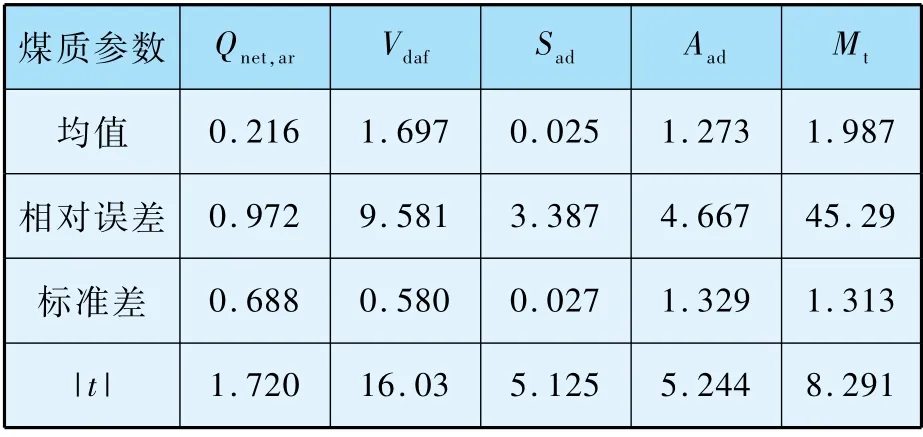
表5 煤质参数实测值和加权值偏差统计结果
查询t分布表,有tα/2(30 -1) =2.045(α取0.05),发现只有Qnet,ar的|t|值小于该值,因此认为只有Qnet,ar具备可加性,而混煤的Vdaf、Sad、Aad和水分不具备可加性,水分相对误差很大,这是由于水分经常变动,故混煤水分不宜用可加性计算。
对Vdaf、Sad和Aad进行线性拟合,将加权计算值作为自变量,实测值作为因变量,拟合结果如图3 所示。
图3(a)为挥发分Vdaf拟合结果,拟合公式如下:
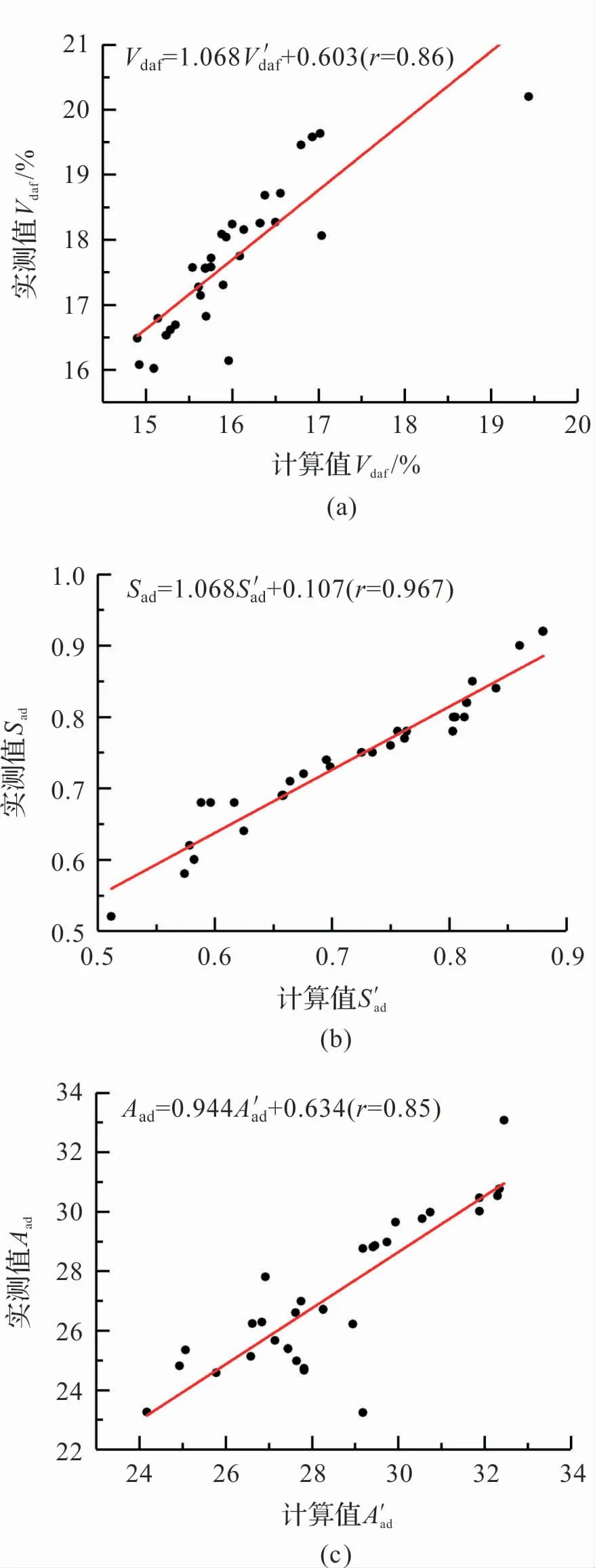
图3 混煤V daf、S ad、A ad拟合结果

因此,本文在对混煤煤质的计算中,发热量采用加权平均值,挥发分、硫分和灰分使用拟合公式,而水分不宜通过计算得到。
2.3 配煤模型输出供煤方案
依据电厂锅炉设计煤种和实际燃烧运行工况,并结合电站运行人员反馈的建议,整理出锅炉燃烧对煤质参数重要性排序和要求范围,如表6所示。
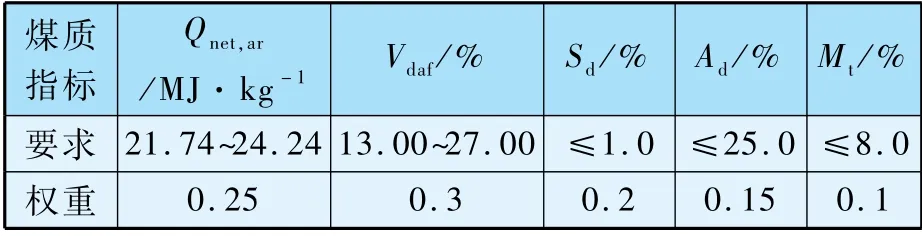
表6 煤质参数权重和要求范围
依据混煤煤质计算方法和配煤模型,以2021年5 月5 日至2021 年5 月10 日期间转入煤场的单煤为例,不同配煤目标输出不同供煤方案,如下表所示。 表7 所示的掺配方案包括混煤煤种和对应配比,具有实际的可操作性。
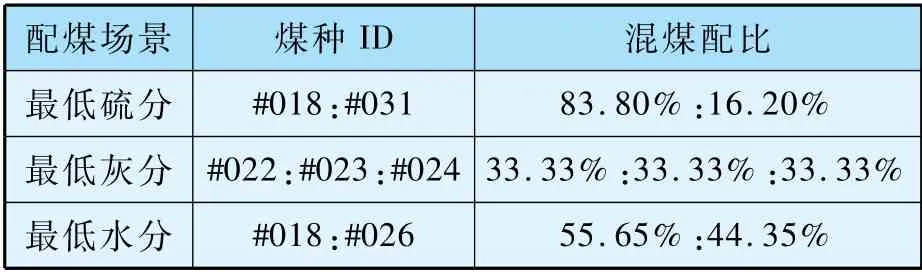
表7 不同配煤目标下的掺配方案
2.4 入炉煤历史化验数据分析结果
图4 为入炉煤质历史化验数据,发热量Qnet,ar主要集中在21 ~24 MJ/kg之间,普遍大于设计煤种21.69 MJ/kg,可能造成锅炉运行调整困难,加大烟温偏差;挥发分呈现大部分集中的特点,绝大部分挥发分在14% ~20%之间,满足设计煤种15.64%的要求;而硫分分布较为分散,在0.5% ~1.0%之间都有相当的占比,不稳定,硫分较大波动容易造成SO2排放突然超标;灰分要求不大于25%,而几乎存在一半位于25%以上,造成不完全燃烧损失较大,受热面积灰结焦严重。
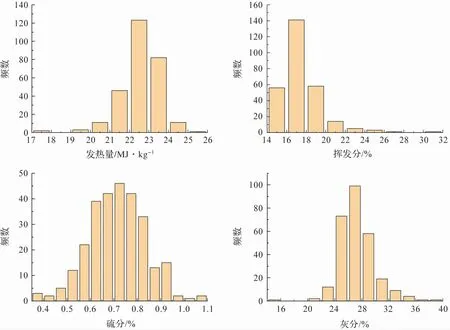
图4 入炉煤发热量、挥发分、硫分和灰分频数分布图
对入炉煤灰分Ad、高位发热量Qgr,d、低位发热量Qnet,ar的实测数据进行统计分析,以灰分Ad作为自变量,高位和低位发热量作为两个因变量,得到图5(a)所示结果,回归方程为式(11)和式(12);以高位发热量Qgr,d为自变量,低位发热量Qnet,ar为因变量,得到图5(b)所示结果,回归方程为式(13)。
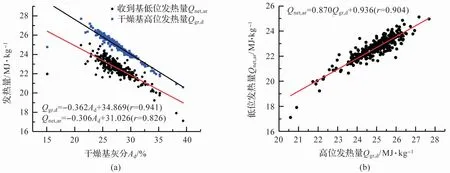
图5 入炉煤发热量和灰分的分析结果

从图5(a)和式(12)可以看出收到基低位发热量Qnet,ar和干燥基灰分Ad之间的线性拟合关系并不是很好,其相关系数仅为0.826,依据线性相关系数较高的式(11)和式(13),得到下式:
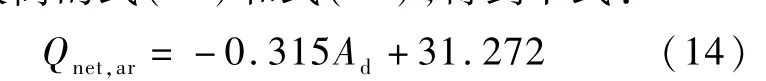
采用式(15)所示的均方根误差(RMSE)和(16)的平均绝对误差(MAE)两个指标来评价式(12)和式(14)的计算结果,如表8 所示。
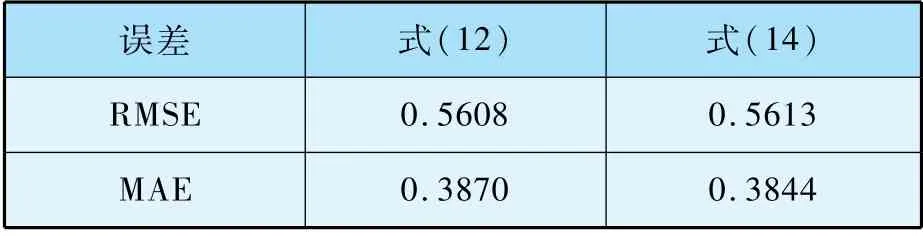
表8 不同计算公式的误差比较
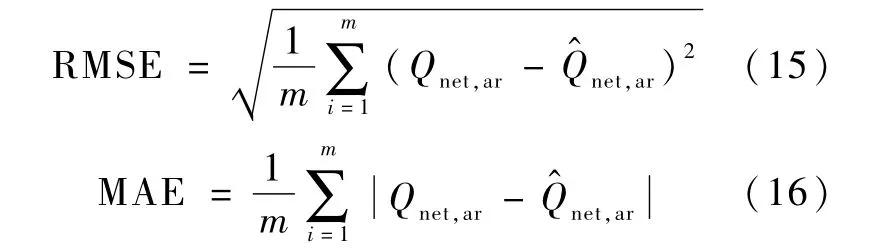
上式中,m 为样本数量;Qnet,ar为发热量实测值,MJ/kg;Q^net,ar为发热量计算值,MJ/kg。
若使用RMSE作为衡量指标,式(12)计算结果较好;若使用MAE作为衡量指标,式(14)计算结果较好。
2.5 入炉煤质计算结果与化验结果对比
配煤模型基于多目标的数学规划问题,依据运行实际,对煤质参数赋予不同权重,在实现锅炉对煤质参数要求的前提下,满足不同配煤目标,输出可供运行人员实际操作的供煤方案。 基于该实际方案,结合入厂煤到入炉煤流程的正向跟踪和逆向溯源的方法,由入厂煤化验的发热量和挥发分等煤质数据,加上混煤煤质计算方法,预测得到皮带入炉煤参数,如表9 所示。
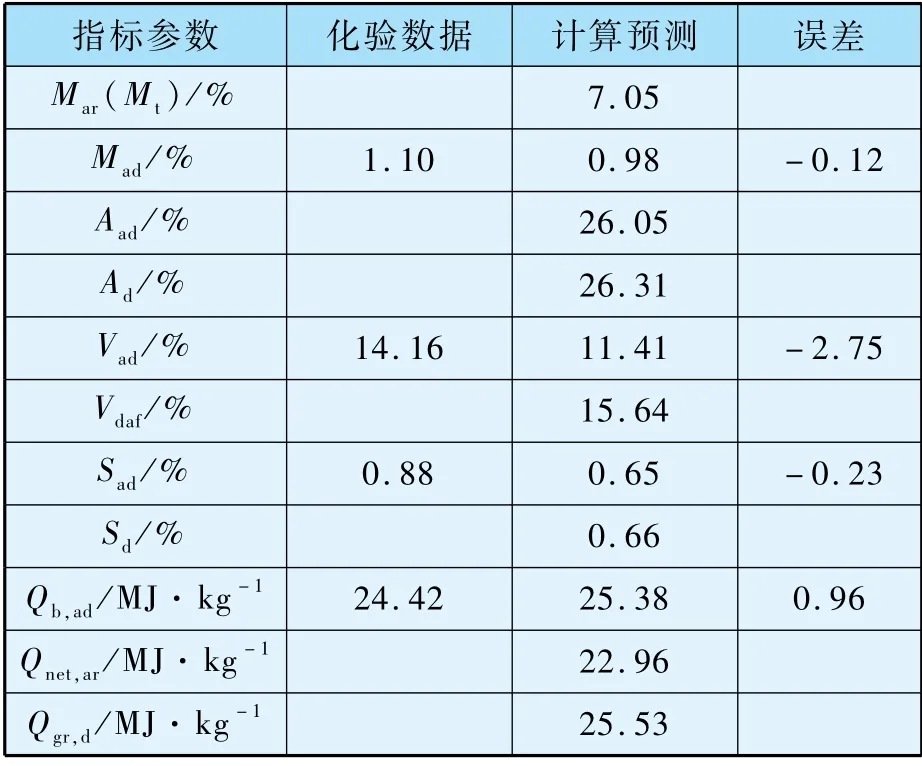
表9 入炉煤参数化验值和预测值比较
显然,预测结果得到的煤质参数更多,更全面,绝对误差也较小。 更重要的是,在时间层面,预测结果相对于发布化验结果可以提前10 余小时,很好地提高入炉煤获取的实时性。
上述获取入炉煤煤质的方法已经成功应用到电厂数据系统中,以低位发热量为例,得到图6 所示的一段时间内的预测值和化验值的比较。
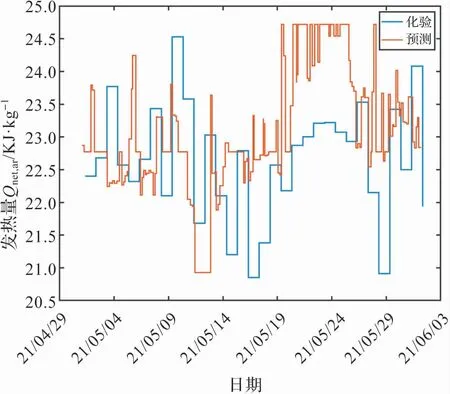
图6 发热量预测值和化验值的比较
该系统将不断增加的入炉煤化验数据和预测结果间的误差作为反馈,不断修正预测模型和计算公式,使得预测值不断接近化验值。
3 总结与展望
针对某煤场过去依靠人工经验配煤,缺乏可靠的配煤掺烧方案指导的问题,构建符合锅炉燃烧对煤质要求的配煤模型。 依据不同配煤目标,输出可实际操作的配煤方案,得到适用性较高的混煤煤质计算方法。 针对入炉煤化验结果滞后,无法指导锅炉运行的现象,提出全流程时空动态跟踪来煤从入厂至入炉的环节。 利用配煤模型、入厂煤化验数据和混煤煤质计算方法,计算得到入炉煤质参数。 与入炉煤实际化验结果相比,不仅计算得到煤质参数更多、误差较小,更可提前10 余小时获知入炉煤质数据。 本文提出的基于动态跟踪的理念,为电厂入炉煤煤质获取提供一种新的思路。
需要指出的是,本文得到的入炉煤参数距离进入炉膛燃烧仍存在一定时间差,为了更准确监控煤质波动,为锅炉运行调整提供预报信息,后续需要进一步研究制粉系统特别是原煤斗和磨煤机对入炉煤参数的影响。
