水库降水速度对大坝上下游边坡安全系数和失效概率的影响研究

李东贤，王上上，杨正权，林后来，刘志良，高 原，李 亮,*，胡 俊

(1.青岛理工大学 土木工程学院，青岛 266525；2.中国水利水电科学研究院 岩土工程研究所，北京 100048；3.青岛新华友建工集团股份有限公司，青岛 266101；4.海南大学 土木建筑工程学院，海口 570228)

滑坡是我国常见的地质灾害之一。在众多的滑坡诱因中，水的变化是主要因素[1]。譬如，库水位骤降常常会导致水库大坝边坡失稳[2-7]，究其原因在于：一方面，渗透性较差的筑坝材料中孔隙水压力来不及消散，导致土体中有效应力减小，土体抗剪强度降低，坝体中浸润线下降速度明显落后于库水位下降速度；另一方面，库水位下降导致坡外水体提供的静水压力消失，不利于大坝边坡的稳定，最终诱发滑坡发生。因此如何控制水库降水速度对水库大坝边坡的稳定性至关重要。目前国内外学者对库区涉水边坡的稳定性做了大量的研究。贾苍琴等[8]研究了在非饱和非稳定条件下库水位骤降下水库大坝的安全系数变化规律，但没有考虑降水速度对大坝边坡最大失效概率的影响；张珂峰[9]、江强强等[10]、张文杰等[11]、贺可强等[12]研究了非饱和土质边坡在降雨及水位变化条件下的稳定性；仉文岗等[13]研究了库区水位下降期间坝体渗透系数等因素变化对边坡安全系数的影响；LANE等[14]采用强度折减方法分析了水位缓降以及水位骤降两种极端情况下土坡稳定性；顾慰慈[15]研究了不同降速系数下，无黏性土和黏性土安全系数的变化规律，并通过安全系数比值下降幅度来确定骤降和缓降；崔洁[16]采用极限平衡方法仅分析了某水电站右岸边坡在不同库水位升降速度情况下安全系数的变化规律，但缺乏对左岸边坡稳定性的分析；田野等[17]研究了不同k/v工况下滑坡的渗流稳定性，重点分析了边坡的稳定性系数变化规律以及浸润线分布规律。已有研究大多集中在库水位下降以及下降速度对大坝稳定性的影响，忽略了不同库水位下降幅度下，下降速度对大坝上、下游边坡安全系数和失效概率的影响。因此，本文通过控制库水位下降高度，研究了库水位的下降以及不同降水速度下，大坝上、下游边坡安全系数的变化，并得到不同库水位下降速度对应的边坡最大失效概率曲线图，通过改变大坝上游坡角值，绘制出大坝上、下游边坡最小安全系数随坡角比值变化曲线图。

1 水库大坝渗流场分析

为了模拟水库降水速度对大坝边坡稳定性的影响，首先需要进行大坝渗流场模拟。在库水位下降过程中，大坝渗流场的变化是一个非稳定、非饱和的过程。其控制微分方程可用达西定律(RICHARDS，1931和CHILDS 等，1950)来描述，达西定律不仅适用于饱和土的渗流，同时也适用于非饱和土的渗流，两者不同之处在于：非饱和土的渗透系数不再是常数，而是体积含水量和孔隙水压力的函数。在t时刻，二维渗流场的控制微分方程：

(1)

式中：H为总水头，m；kx，ky分别为x，y方向的渗透系数，m/s，Q为边界流量，q；θ为体积含水量。

设ua为孔隙气压力，uw为孔隙水压力。本文假定在非饱和土体中，土体内体积含水量的改变只与土体内基质吸力(ua-uw)有关系，且只是孔隙水压力的函数：

∂θ=mw∂uw

(2)

式中：mw为土体含水量曲线上一点的斜率。

考虑到总水头H如式(3)所示：

(3)

式中：H为总水头，m；γw为水的重度，kN/m3；y为高程，m。

将式(2)(3)代入式(1)，得

(4)

在非饱和土体中，体积含水量函数表示土体中现有的含水量，土体中水的含量决定着土体中水的流动能力，流动能力的强弱用渗透系数的大小来表示，同等条件下，体积含水量越高，渗透系数越大，反之亦然。

2 非饱和土边坡稳定性分析

在获取t时刻的大坝渗流场之后，可以采用传统的极限平衡方法进行非饱和土边坡稳定性分析。与饱和土边坡稳定性分析不同的是，非饱和土边坡需要考虑基质吸力对土体抗剪强度的影响，最具代表性的非饱和土抗剪强度公式是由BISHOP(1960)和FREDLUND(1978)提出的，本文采用FREDLUND等[18]提出的以有效应力分量为基础的双应力状态变量公式：

τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb

(5)

式中：τf为抗剪强度，kPa；c′为有效黏聚力，kPa；ua为孔隙气压力；uw为孔隙水压力；σ为土体总应力，kPa；φ′为有效摩擦角，(°)；φb为与基质吸力(ua-uw)有关的内摩擦角，(°)。

基质吸力会增加边坡土体的抗剪强度，有利于边坡的稳定性。由于和大气连通，一般认为孔隙气压力ua=0，在Slope/w程序中采用Morgenstern-Price法进行边坡稳定性计算，与常规的计算过程不同在于：在非饱和土条件下，Seep/w获得的孔隙水压力和基质吸力导入Slope/w，用于计算基质吸力对土体抗剪强度的贡献。

3 数值模拟验证

3.1 模型试验

应用本文方法对文献[19-20]开展的模型试验过程进行了数值模拟并与试验结果进行对比，以此来验证本文方法的可行性和有效性。如图1所示，该模型边坡高程为5.8 m，基底厚2 m，坡角为31.5°，边坡模型采用砂质粉土材料填筑，其参数为：重度γ从上到下按18.06～18.58 kN/m3线性分布，黏聚力c=0.4 kPa，内摩擦角φ= 30°，饱和渗透系数为5.3×10-6m/s。试验模型在水位上升到6 m，完全浸泡72 h后水位开始下降，所以数值模拟采用饱和土进行分析。

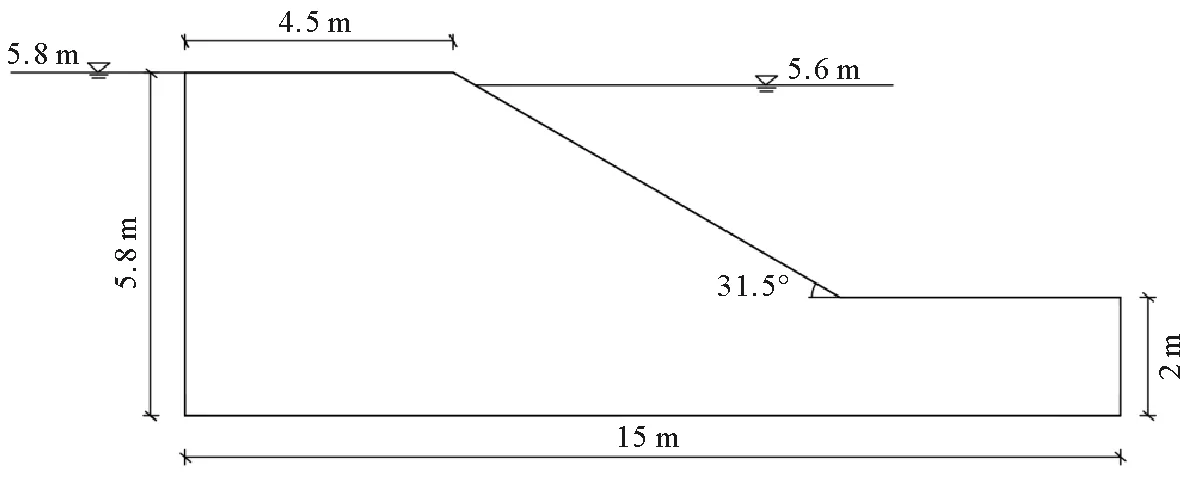
图1 边坡模型

3.2 边坡降水失稳数值模拟

本次数值模拟采用Geo-Studio中的Seep/w模块来模拟边坡外水位的下降，与试验一致，下降速度为1 m/h，通过设置不同的时步，分别模拟了边坡水位下降0.7 m (t1时刻)、1.7 m(t2时刻)、1.75 m(t3时刻)时刻模型边坡的渗流场，在不同时刻渗流场模拟的基础上，利用Geo-Studio中Slope/w模块，选择bishop法进行边坡稳定性计算，如图2所示。

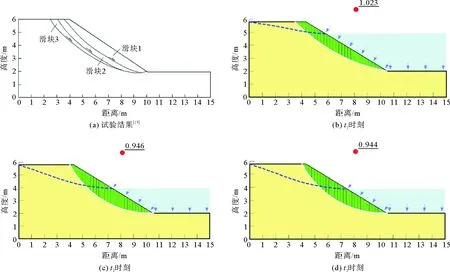
图2 降水过程不同时刻边坡稳定性分析与试验结果对比

由图2可以看出，在坡外水位下降15 min时，坡肩出现张拉裂缝；当试验开始40 min，水位下降约0.7 m的时候，滑块1产生滑动，滑块1背后的坡体处于较稳定的状态；随着水位的继续下降，在试验进行到100 min，水位下降约1.7 m时，滑块2形成且为典型的旋转滑坡；在试验进行稍后不久，滑块3产生滑动，试验得到的滑块的滑面如图2(a)所示。在t1时刻，边坡水位下降0.7 m时，模型边坡安全系数接近1.0，表明边坡处于临界滑动状态，图2(b)所示滑动面为最危险滑动面，与试验所得滑块1形状保持一致(图2(a))；在t2，t3时刻，水位分别下降1.70和1.75 m时，可以看到模型边坡在原来基础上又产生滑动，由于试验中滑块1产生滑动，此时边坡模型已发生改变，在数值模拟中进行简化，从图2(c)(d)与图2(a)滑动面的形状对比分析，与滑块2和滑块3大致相同。由图2(b)—(d)数值模拟分析得到的结果与图2(a)模型试验得到的结果大致相同，验证了本文数值模拟方法的可行性和有效性。

4 算例分析

4.1 水库大坝模型与土体参数

如图3所示，为典型的均质大坝，高程为34 m，基底厚10 m，底边界为不透水边界，大坝上、下游边坡高为24 m，上、下游坡面水平投影长度为32 m，上、下游坡角均为36.87°。大坝坝体材料参数为：重度γ=18.8 kN/m3，黏聚力c=25 kPa，内摩擦角φ=25°，饱和渗透系数K为8.64 m/d。上游初始水位H0=30 m，死水位H1=14 m，下游水位位于坡底。

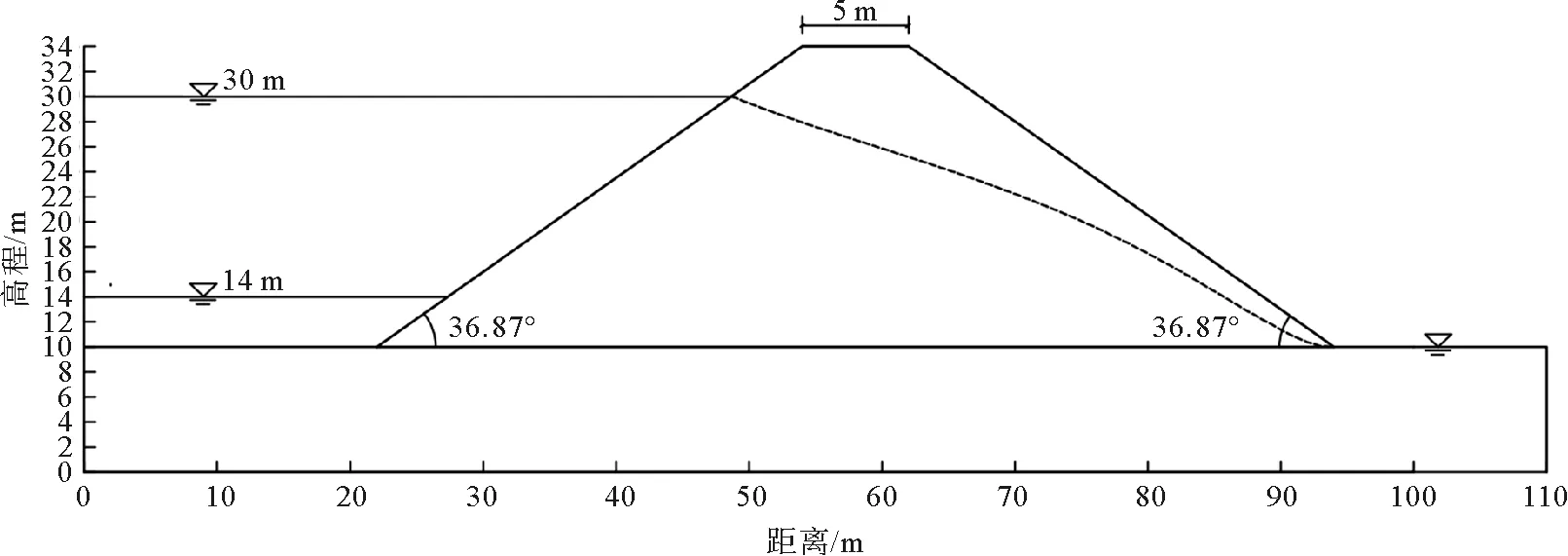
图3 水库大坝模型

在非饱和非稳定渗流条件下，为了考虑库水位下降速度对大坝上、下游边坡稳定性的影响，在Seep/w模块中设置水头边界函数，定义边界水头H和时间t的关系，来模拟不同的降水速度。设库水位降水速度为1 m/d，库水位降幅为16 m，即如果水位从30 m下降到14 m，则边界函数可以设置第0天水头H为30 m，第16天水头H为14 m。类似地，如果水位下降的速度为2 m/d，则可以设置第8天的水头H为14 m，这样便实现了大坝上游库水位不同下降速度。在不同的计算时刻，由Seep/w可以获得大坝的渗流场，进而获取相应时刻的浸润线，然后利用Slope/w计算相应时刻的大坝上、下游边坡最小安全系数。

4.2 边坡渗流与稳定性分析

大坝库水位由初始水位H0=30 m开始下降，考虑两种降水幅度，第一种降幅是16 m，即自H0降水至H1(14 m)，第二种降幅是8 m，即自H0降水至(H0+H1)/2，通过Seep/w程序设置库水位下降过程保存时步时长为1 d，图4、图5分别给出了第一、二种降幅不同降水速度下浸润线的变化过程。如图4所示，在第一种降幅下，当降水速度为1 m/d时，随着库水位的下降，靠近上游边坡处的浸润线下降速度较快，上游位置浸润线与坡表面重合，大坝坝体中的浸润线下降速度较慢，坝体浸润线呈现出上凸的形状，这是由于大坝坝体中的水由于受到土体渗透系数的影响，导致向外渗流速度远远小于坡外水位的下降。当降水速度为2，4 m/d时，坝体浸润线形状与降水速度为1 m/d时一致。从浸润线上凸点位置来看，在第一种降幅完成后，1，2，4 m/d降水速度下，浸润线上凸点高程分别为23，25，26 m，由此可见，随着降水速度的增加，浸润线位置越高，这是由于水位下降速度较小时，坝体中水向外渗流比较充分。由图5可以得到类似图4的结论，在此不再赘述。

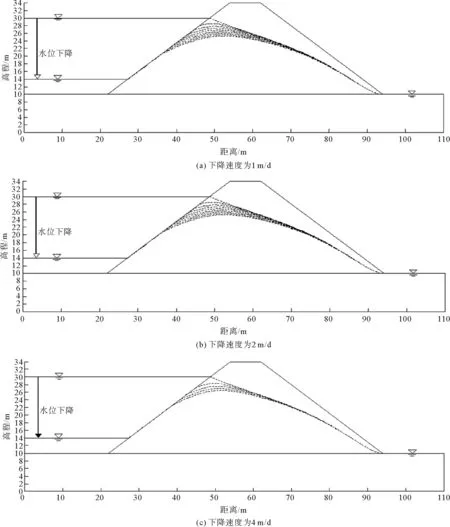
图4 大坝浸润线变化过程(第一种降幅)

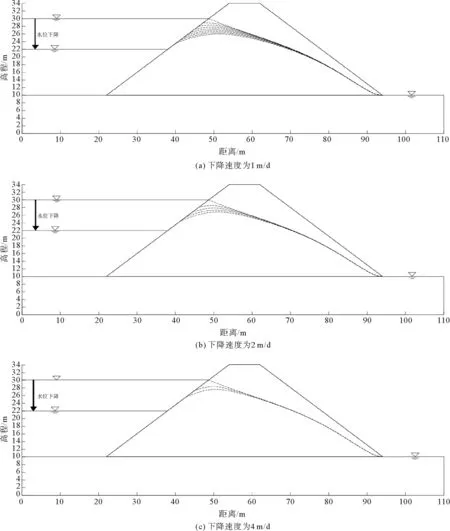
图5 大坝浸润线变化过程(第二种降幅)

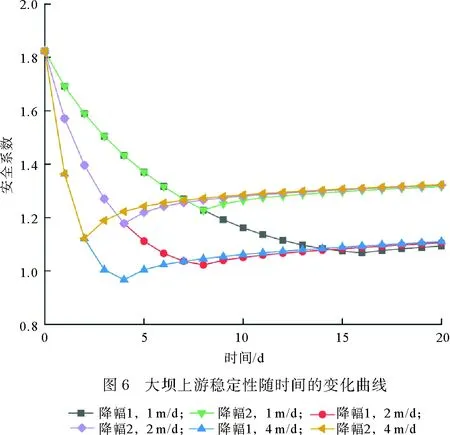
基于Seep/w获得的渗流场来分析大坝上、下游边坡稳定性，计算每一时步(本文为每天)上、下游边坡的最小安全系数，并绘制安全系数与时间的关系曲线，为了得到库水位降幅完成后坝体稳定性变化过程，将分析时步设置为20 d，即在降幅完成后继续进行大坝渗流场的分析，获取其浸润线并计算其最小安全系数。图6、图7分别给出了1，2，4 m/d降水速度时，上、下游大坝边坡最小安全系数随计算时步的变化曲线。由图6可见，在库水位下降16 m情况下，1 m/d降水速度下，降水开始的刹那，大坝上游边坡最小安全系数是1.82，降水1 d后，降至1.69，2 d后，降至1.59，其后随着计算时步的增加，最小安全系数逐渐减小，16 d后，第一种降幅完成，即库水位降至死水位，最小安全系数降至1.07，其后随着计算时步的增加，安全系数略有增加，其后基本不再变化，20 d后，安全系数稳定在1.09。由此可见，大坝上游边坡最小安全系数随着库水位的下降而减小，降幅完成初始时刻安全系数降到最低值，其后，随着计算时步的增加，其安全系数开始增加，直至稳定在某一数值左右。在降幅未完成时，随着库水位的下降，坡外水体逐渐消失，由于该水体对大坝上游边坡起抗滑作用，因此上游边坡安全系数随着库水位的下降而减小，在降幅完成后，坡外水体不再变化，然而由于坝体内浸润线不断下降，超孔隙水压力的消散有利于边坡稳定性，因此降幅完成后，随着计算时步的增加，安全系数又逐渐增加。2，4 m/d降水速度时，最小安全系数随计算时步的变化规律与1 m/d降水速度基本一致。区别之处在于：2 m/d降水速度时，降幅完成时刻的最小安全系数为1.02，4 m/d降水速度时最小安全系数为0.96，由此可见，随着降水速度的增加，降幅完成时刻的最小安全系数逐步减小。这是由于降幅完成时，有利于坝体稳定的坡外水体消失，但降水速度快时，坝体浸润线较高，由此导致大坝上游边坡的安全系数较之降水速度慢时要小；不同降水速度下，降水14 d后的安全系数基本一致。由库水位下降8 m情况下，可以发现相类似的规律。不同之处在于，由于第二种降幅小，有利于上游坝坡稳定的坡外水体消失的少，因此，同等条件下，第二种降幅下上游坝坡最小安全系数较之第一种降幅下要高。

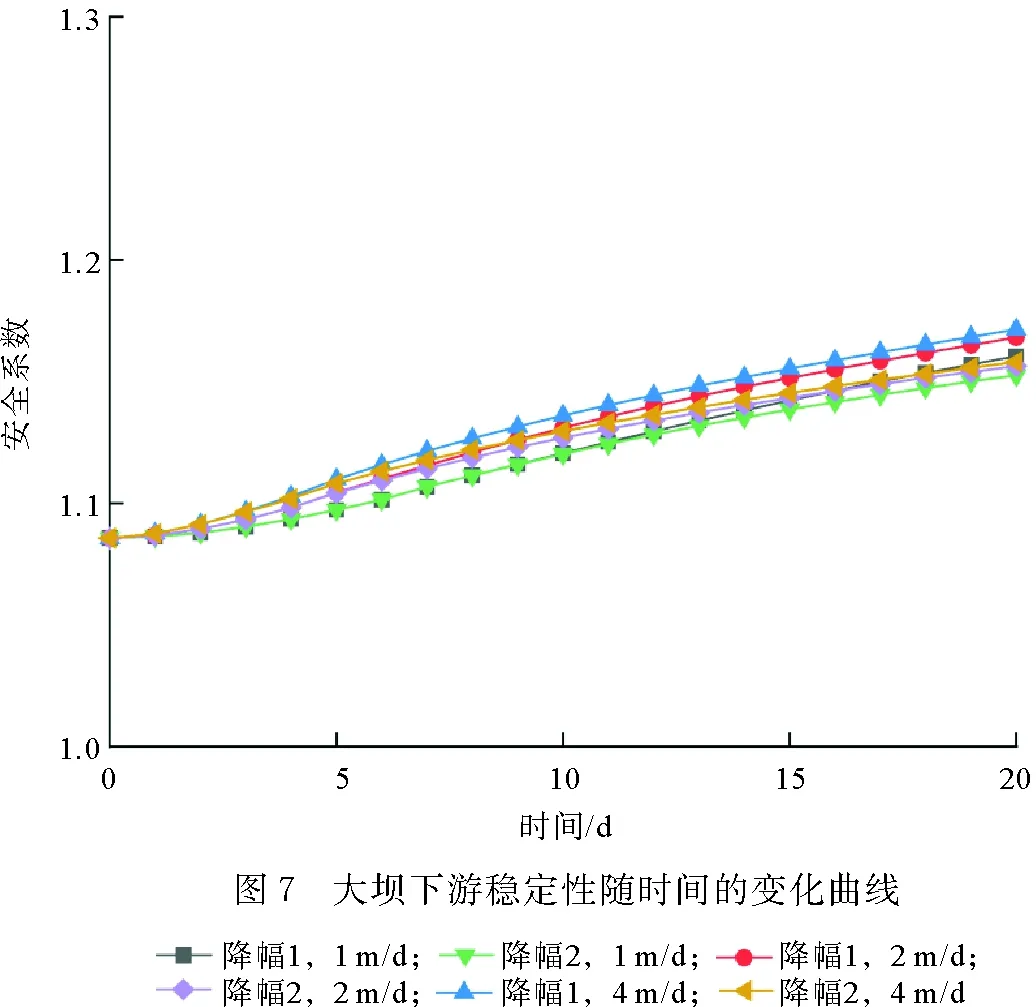
从图7可知，在库水位下降16 m的情况下，1 m/d降水速度下，降水开始的刹那，大坝下游边坡最小安全系数是1.085，其后随着计算时步的增加，最小安全系数在逐渐增加，在16 d时，升至1.15，其后随着计算时步的增加，安全系数仍逐渐上升，在20 d时，升至1.16。由此可见，大坝下游边坡的最小安全系数随着库水位的下降而增加，但是增幅不大。随着库水位的不断下降，大坝体内超孔隙水压力不能及时消散，然而坡外自由水提供的浮力作用较小，坝体的抗滑力仍然需要以总重来计算；随着库水位的不断下降，坝体内超孔隙水压力的消散，滑动面上法向有效应力逐渐增加，土坡的安全系数不断增大。2，4 m/d降水速度时，最小安全系数随计算时步的变化规律与1 m/d降水速度基本一致，区别之处在于：2 m/d降水速度时，最小安全系数在8 d时，升至1.13；4 m/d降水速度时，安全系数在4 d时，升至1.1。由此可见，随着降水速度的增加，降幅完成时刻的最小安全系数在逐渐减小，但是减幅不大，这是由于坡外自由水对大坝下游影响较小，随着降水速度的增加，坝体内浸润线较高，由此导致大坝下游边坡的安全系数降低。由库水位下降8 m情况下，可以发现有类似的规律。不同之处在于：由于第二种降幅较小，坝体内超孔隙水压力消散较少，因此，在同等条件下，第二种降幅中下游坝坡安全系数较之第一种降幅较低。

4.3 边坡失效概率分析

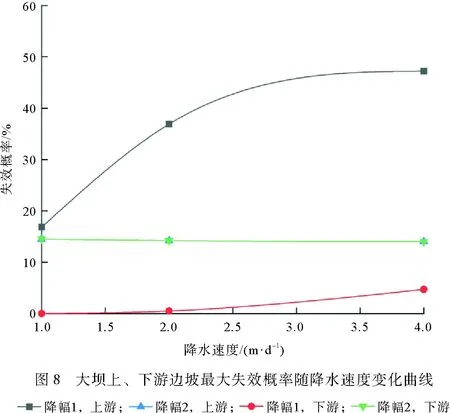
由于大坝材料的不确定性，仅用安全系数来评估上、下游边坡的稳定性不够全面，本节视其黏聚力c和内摩擦角φ为对数正态随机变量，其均值和标准差分别为25 kPa，5 Pa和25°，5°。三种降水速度1，2，4 m/d分别记为V1，V2，V3。针对图6、图7中的每一工况，计算上、下游边坡的失效概率。采用4.1，4.2节相同计算模型与时步，在第一种降幅、降水速度V1的某个时步条件下，利用Matlab软件产生2000个c，φ样本值X1，X2，…，X2000，其中Xi=(ci，φi)。基于极限平衡方法中的Morgenstern-Price法计算2000个土体参数样本对应的M=2000个安全系数，记为Fs1，Fs2，…，Fs2000。在M=2000个安全系数中，若安全系数Fsi<1，则称Xi为失效样本，如此重复进行共获取m个失效样本， 利用m/M计算出大坝各个时步样本对应的失效概率Pf1，Pf2，Pf3，…，Pf20，从各个时步对应的失效概率Pf1，Pf2，Pf3，…，Pf20中取最大值，记为第一种降幅、降水速度V1对应的最大失效概率Pfmax1，如此重复计算，可利用(Vi，Pfmaxi)i=1，2，3绘制第一种降幅下，降水速度与大坝上游边坡最大失效概率关系曲线。变换第二种降幅，进行如上相同操作，可以获得第二种降幅下，降水速度与大坝上游边坡最大失效概率关系曲线。类似地，也可以获得在第一、二种降幅下，降水速度与大坝下游边坡最大失效概率关系曲线。计算结果如图8所示。由图8可见，在第一种降幅下，降水速度V1，V2，V3下，大坝上游边坡最大失效概率分别为0.168，0.369和0.472；在第二种降幅下，降水速度V1，V2，V3下，大坝上游边坡最大失效概率分别为0，0.005和0.047，由此可见，随着降水速度的增加，大坝上游边坡最大失效概率呈现明显增加趋势，降水速度对上游边坡失效概率影响显著。反观下游边坡，在第一、二种降幅下，下游边坡最大失效概率基本不变。对本例而言，降水速度对大坝上游边坡影响明显大于下游边坡。从失效概率数值来看，第一种降幅下上游边坡最大失效概率最高，下游边坡最大失效概率居中，第二种降幅下上游边坡最大失效概率最低。由此可见，降水速度和库水位降幅对上游边坡的失效概率影响显著，对下游边坡影响不大。由图6、图7可知，第二种降幅下，上游边坡的最小安全系数介于1.12～1.23，与下游边坡的最小安全系数相差不大。而从图8的失效概率对比来看，第二种降幅下，上游边坡的失效概率明显小于下游边坡的失效概率，由此证明：当库水位降幅变化时，上、下游边坡的稳定程度也随之发生改变，当降幅较大时，上游边坡稳定性是控制工况；当降幅减小后，下游边坡稳定性有可能成为控制工况，因此，在库水位下降时，要综合分析降幅和降水速度对大坝边坡稳定程度的影响。

4.4 坡角对大坝稳定性的影响

以上研究假定上、下游边坡坡角相等，本小节拟研究大坝上游边坡坡角变化对计算结果的影响。原上游边坡坡角为φ0=36.87°，下游边坡坡角保持不变，现假设大坝上游坡角为一可变值φx，令φx/φ0=0.4，0.8，1.2，1.6，2.0，在某一φx下，基于4.2节计算步骤，可以得到同一降幅、同一降水速度下，大坝上、下游边坡安全系数随时间的变化曲线，为研究方便，取变化曲线上的最低点，即最小安全系数作为该降幅、降水速度下边坡的最小安全系数。变换φx值，重复进行计算，可以得到不同降幅、不同降水速度下，上、下游边坡最小安全系数随坡角比值的变化曲线，如图9、图10所示。图9给出了第一种降幅下，上、下游边坡最小安全系数随坡角比值的变化曲线。由图9可见，坡角比值从0.4变化至2.0的过程中，降水速度1 m/d下，上游边坡最小安全系数值从1.92迅速下降至0.72；降水速度2 m/d下，上游边坡最小安全系数值从1.85迅速下降至0.70；降水速度4 m/d下，上游边坡最小安全系数值从1.75迅速下降至0.66。由此可见，随着坡角比值的增大，上游边坡坡角渐趋增大，不利于保持稳定，最小安全系数逐渐减小。由4.2节的研究结论可知，降水速度增加，上游边坡最小安全系数减小，反映在图9中，降水速度1 m/d下的曲线位置最高，4 m/d最低。下游边坡最小安全系数随着坡角比值的增大，缓慢减小，当坡角比值为0.4时，下游边坡最小安全系数为1.14；坡角比值为2.0时，其值变化为1.10。

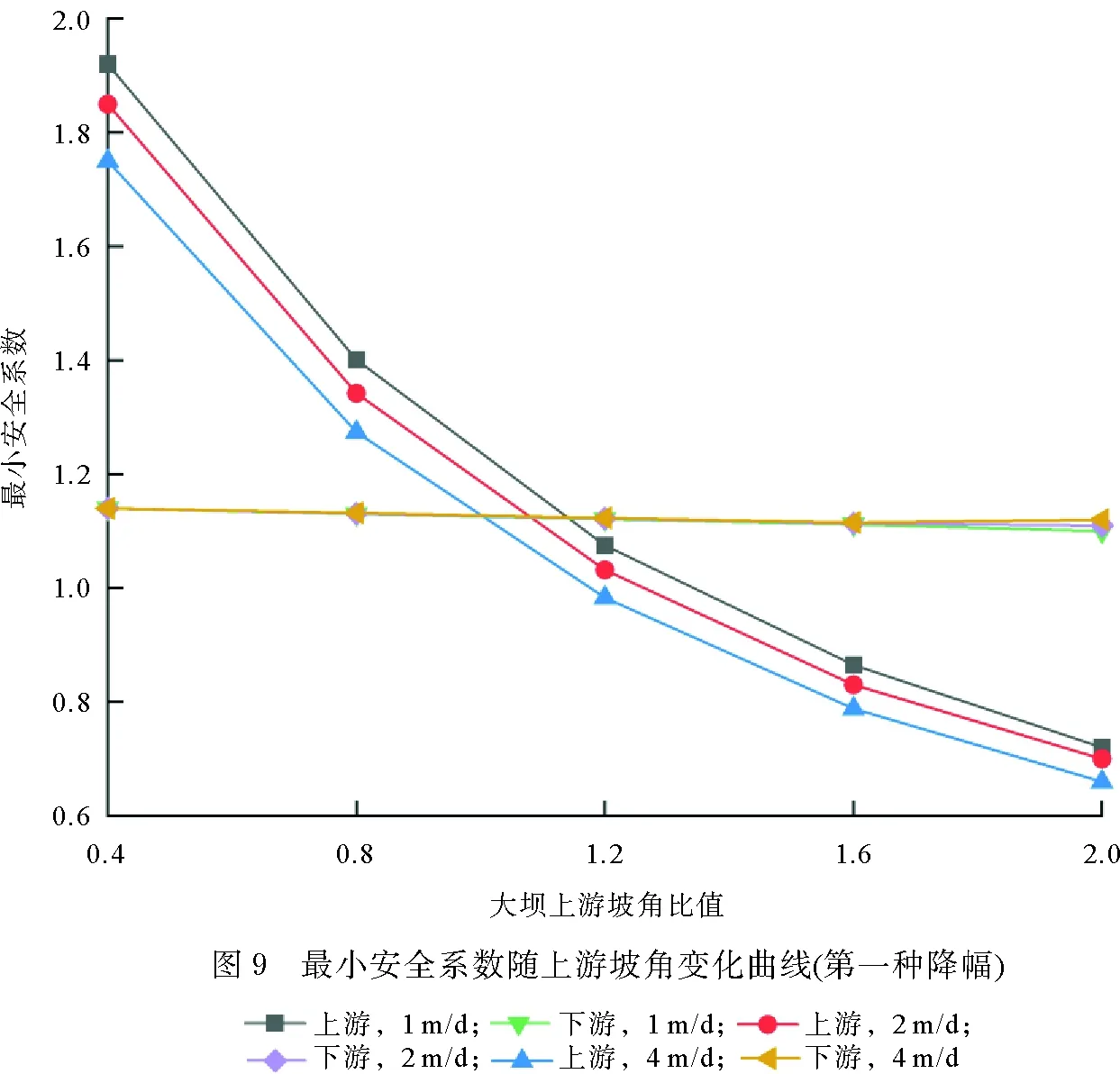
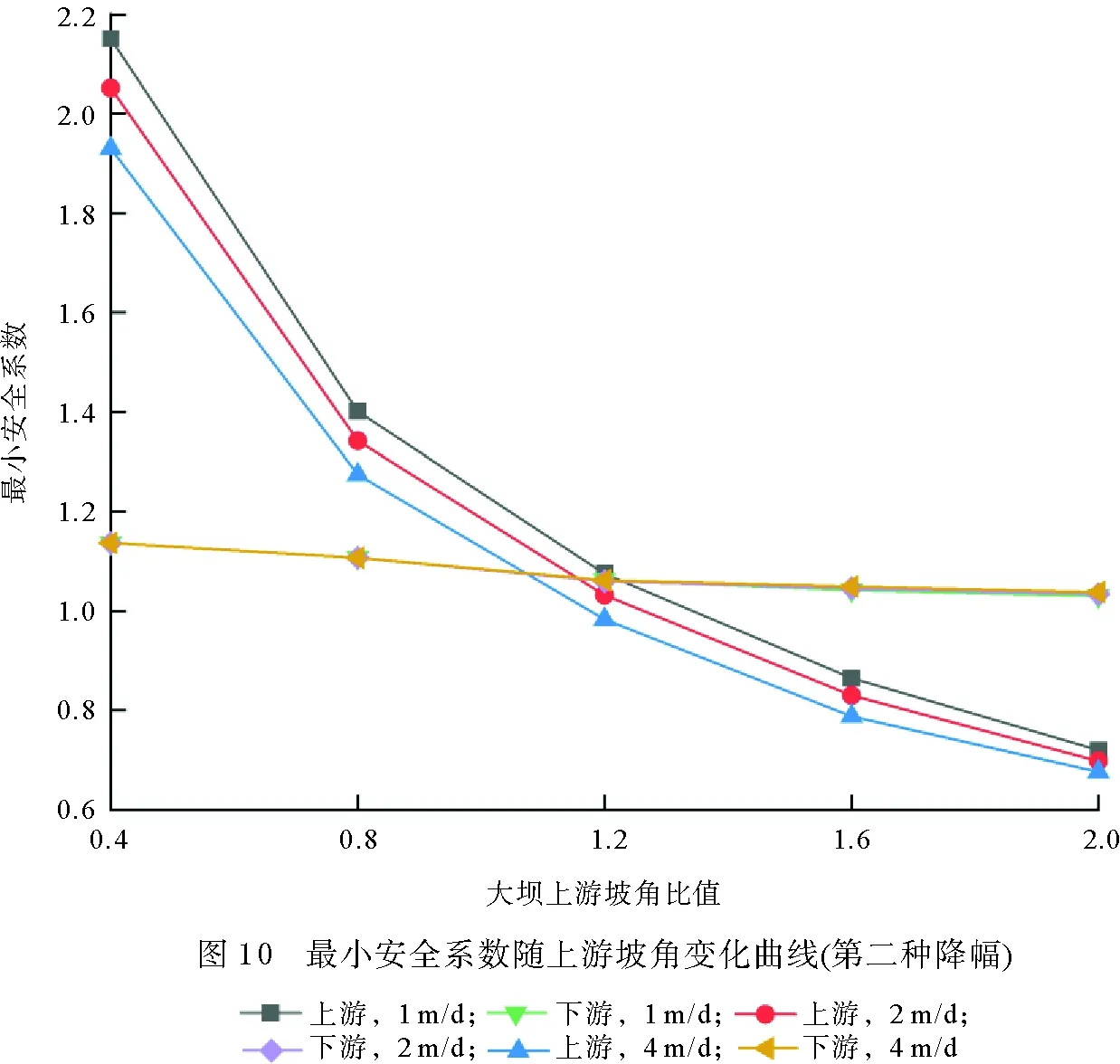
相同降幅和相同降水速度下，上游边坡最小安全系数变化线与下游边坡最小安全系数变化线会交于一点，记为该降幅和降水速度下的临界坡角比值。当坡角比值大于临界坡角比值时，上游边坡最小安全系数小于下游边坡最小安全系数。反之亦然。随着降水速度的增加，临界坡角比值逐渐减小。图10给出了第二种降幅下，上、下游边坡最小安全系数随坡角比值的变化曲线。由图10可以得到类似于图9的变化规律。区别之处在于：第二种降幅下，临界坡角比值较之第一种降幅下有向右偏移的趋势。因此，在大坝上、下游边坡稳定程度比较时，要综合考量坡角比值、降幅和降水速度的影响。

5 结论

1) 在正常情况下，随着库水位的下降，靠近边坡处的浸润线下降速度较快，大坝坝体中的浸润线下降速度较慢，坝体浸润线呈现出上凸的形状，这是由于大坝坝体中的水由于受到土体渗透系数的影响，导致向外渗流速度远远小于坡外水位的下降，上游位置浸润线与坡表面重合。

2) 在库水位两种降幅下，大坝上游边坡最小安全系数随着库水位的下降而减小，降幅完成初始时刻安全系数降到最低值，其后，随着计算时步的增加，其安全系数开始增加，直至稳定在某一数值左右，随着降水速度的增加，降幅完成时刻的最小安全系数逐步减小，不同降水速度下，降水14 d后的安全系数基本一致；大坝下游边坡的最小安全系数随着库水位的下降而增加，随着降水速度的增加，降幅完成时刻的最小安全系数逐渐减小。

3) 随着降水速度的增加，大坝上游边坡最大失效概率呈现明显增加趋势，降水速度对上游边坡失效概率影响显著；反观下游边坡，在第一、二种降幅下，下游边坡最大失效概率基本不变。从失效概率数值来看，第一种降幅下上游边坡最大失效概率最高，下游边坡最大失效概率居中，第二种降幅下上游边坡最大失效概率最低。由此可见，降水速度和库水位降幅对上游边坡的失效概率影响显著，对下游边坡影响不大。

4) 随着坡角比值的增大，上游边坡坡角渐趋增大，不利于保持稳定，最小安全系数逐渐减小；下游边坡最小安全系数随着坡角比值的增大，缓慢减小。当坡角比值大于临界坡角比值时，上游边坡最小安全系数小于下游边坡最小安全系数。反之亦然。因此，在大坝上、下游边坡稳定程度比较时，要综合考量坡角比值、降幅和降水速度的影响。