基于集合经验模态分解与希尔伯特-黄变换的有轨电车异常振动分析

闫转芳，张会杰，季元进

（1.中车青岛四方机车车辆股份有限公司，山东 青岛 266000；2.同济大学，上海 200000）

有轨电车在运行时，若车辆发生故障，一些故障信息会在车辆受到线路冲击时，通过异常的振动信号体现出来。异常振动使振动信号在时频特性上发生相应的变化，异常振动信号与正常信号的频率、能量分布以及能量大小都有所不同。对有轨电车振动信号的分析有诸多时域及频域方法，然而以傅里叶变换为代表的传统时频分析方法在处理复杂的故障信号时有一定的局限性[1-2]。有轨电车异常振动信号多为非平稳非线性数据，在对这类信号的处理上，希尔伯特-黄变换（HHT）具有明显的优势。HHT的分解依据为信号本身的时间尺度特性，与小波分解和傅里叶分解等方法的本质区别在于HHT免去了预先设定基函数这一步[3]。

由于信号的内部特征可以由HHT准确地展现出来，且HHT的时频域分辨率相对较高，因此HHT在振动分析、故障检测、参数识别等领域具有重大意义，被广泛地应用。陈双喜等[4]提出利用一种改进的经验模态分解方法，有效地提取车辆-轨道耦合系统的动力学特性。李再帏等[5]利用HHT方法对车辆-轨道系统垂向振动进行时频分析，对轨道高低不平顺与车辆垂向振动加速度的关系进行定量研究。苏鹏等[6]将HHT应用于桥梁的振动分析中，对列车过桥时的振动响应进行处理，为桥梁振动分析与健康检测提供了有力的工具。

本文以某型有轨电车为研究对象，提出了基于EEMD和HHT的有轨电车异常振动分析研究方法。模态混叠问题难以避免地发生在传统HHT采用的经验模态分解当中，针对此问题，本文提出利用集合经验模态分解（EEMD）方法对原始信号进行分解，并利用相关系数法选取真实分量，剔除无意义的虚假分量。对真实分量进行Hilbert变换得到异常振动信号的Hilbert谱，与正常振动状态对比分析，实现有轨电车异常振动与正常振动状态的时频特征区分。对Hilbert积分得振动信号的边际谱，通过边际谱得到异常振动的主频，分析异常振动区段对应的线路问题及故障模式。

1 基本原理

1.1 铁路接头平顺性评判方法

钢轨接头引起的瞬时脉冲经过傅里叶变换后，在频域上是一个无限带宽的信号，在理论上应当存在所有频率的成分，并且各频率成分的能量沿整个频率轴均布。因此该信号成分中必定含有轮对-轴箱系统的固有频率，也就必定会引起系统发生广义共振。基于上述原理，共振解调被用作铁路接头平顺性的评判方法。

铁路接头平顺性评判方法可描述如下。

（1）采集轴箱加速度。

（2）对轴箱垂向振动加速度进行带通滤波，带宽为[20，450]Hz。

（3）计算滤波后的轴箱垂向振动加速度有效值。（4）将有效值进行归一化操作得到接缝不良指数如下

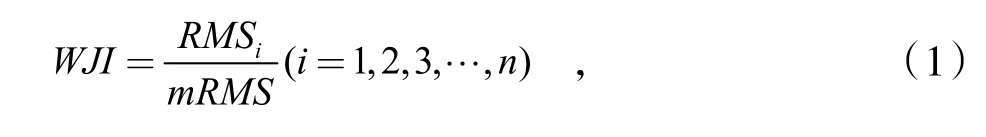
式中：mRMS是有效值的平均值；n是RMS点数。

（5）若接缝不良指数WJI大于4，也就是该处的冲击能量是平均冲击能量的4倍时，则判定接头平顺性不良。

1.2 集合经验模态分解

集合经验模态分解（EEMD）数据分析方法运用噪声辅助，对信号数据叠加高斯白噪声，进行多次经验模式分解，有效解决了经验模态分解（EMD）的模态混叠问题[7]。EMD原理如下：通过对原始信号x（t）的上、下包络线计算出平均包络线m1（t）。用原始信号x（t）减去m1（t）得到一个去掉低频的新数据序列h1（t），通过h1（t）的极值点个数与过零点个数相差不超过1及h1（t）的上、下包络线均值恒为0两点依据判定h1（t）是否为一个本征模分量（IMF）。若不是则重复操作直至得到满足条件的本征模分量，记作c1（t）。c1（t）表示原始信号中的最高频成分。用原始信号x（t）减去c1（t），得新序列r1（t）：将r1（t）作为新的“原始信号”重复以上步骤，直至残余信号分量rn为周期函数、单调函数、常数或仅含一个极值的简单信号函数。原始信号经EMD分解为

式中：ci为所得到的各个IMF分量，包含了信号高频段至低频段的不同成分；rn（t）为残余信号。

EEMD是指在待分解的信号中加入高斯白噪声，将融合白噪声的信号通过EMD分解为多个IMF。由于高斯白噪声拥有频率均匀分布和幅值零均值的特点，因此运用不相同但幅值相等的高斯白噪声，将其加入信号当中，以此来改变信号的极值点特性[8]。由于噪声经过总体平均后被互相抵消，最终结果来自于多次EMD分解以后得到的IMF集成均值，以防止模态混叠的发生。

1.3 相关性检验

EEMD分解得到的所有IMF并非都是有意义的，其中可能包含部分虚假、无意义的分量，如噪声分量和趋势项分量等。各IMF与原信号的相关程度评估是基于相关系数法，相关系数较低的被称为虚假分量，需将其除去。保留真实IMF进行重构，达到降噪的目的[9]。信号中存在一些幅值较小的IMF，其真实存在，但容易被当作虚假分量而被除去。为了防止误删的情况发生，在IMF与原信号计算相关系数前，需要对它们进行归一化处理[10]。归一化相关系数为

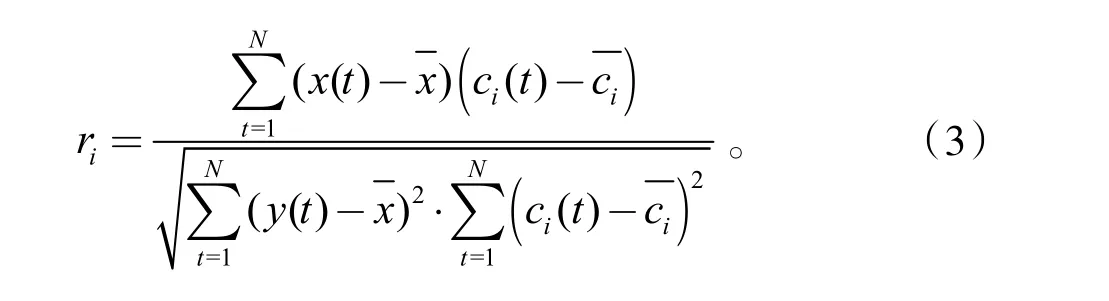
1.4 希尔伯特-黄变换

希尔伯特-黄变换（HHT）将非平稳信号进行平稳化处理，也适用于非线性信号[8]。包含有不同尺度的趋势或波动的信号被逐级分解成为多个IMF，然后将各IMF进行HHT得到时间与频率联合分布的Hilbert谱。原信号的频率含量由瞬时频率与瞬时能量两指标来表征。

其步骤如下：首先，对每个本征模分量ci（t）作Hilb ert变换得到di（t）

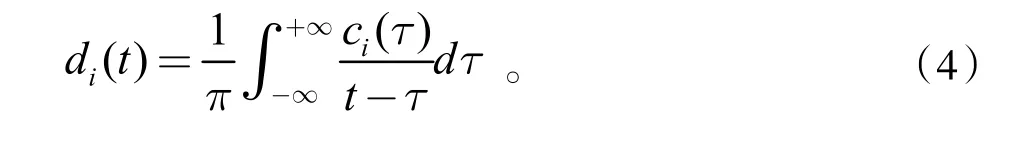
构造解析信号

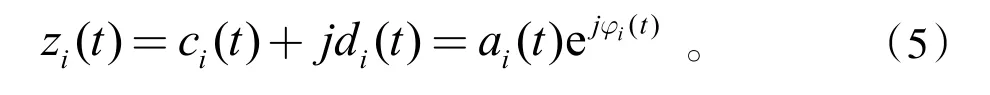
得相应IMF的瞬时幅值为

相位为

进一步可以得瞬时频率

因此，原始信号x（t）可展成

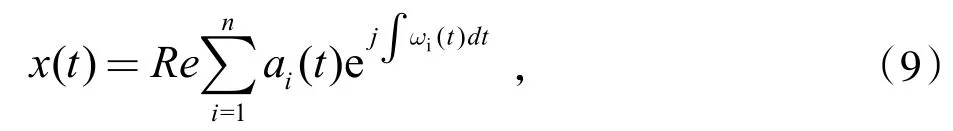
式中：Re表示取实部。式（9）表征了x（t）的时间-频率-幅值的三维关系，将信号幅度在时频上的分布称为Hilbert时频谱，简称Hilbert谱，以H（w，t）表示，其数学表达式为

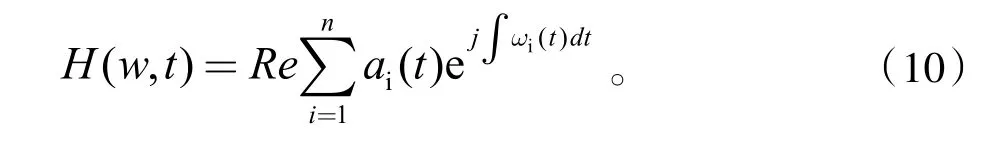
对H（w，t）积分可得Hilbert边际谱h（w）

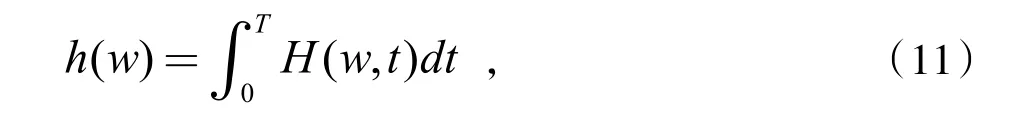
式中：T为信号的总长度。一方面，边际谱反映了信号瞬时频率总幅值的大小，在数理统计角度来说，其表示的是全部所测数据的累加幅值；另一方面，其反映了在信号整个时间段内，每个频率值对累加幅值的贡献。

H（w，t）是一种变化规律，用来代表所测数据的幅值随时间和频率，在整个频段上的变化规律，而h（w）反映的是其变化情况。

2 有轨电车运行试验

本文所进行特征提取与异常振动分析的有轨电车振动数据来自某型有轨电车，整列车包括3节车体与4个转向架，转向架全部为独立轮对转向架，其中车体连接处采用铰接式独立车轮转向架。被测车辆的一、二系弹簧、减振器状态均正常。车轮踏面选用LO67588P踏面。正线直线为50 kg工字轨，轨底坡1/40；部分线路为Ri60R2槽型轨及护轨。

在有轨电车的三位轴轴箱上布置垂向加速度计，压电式，型号为LA0107T-100，量程100 g，测试精度为0.5%。有轨电车编组及测点布置如图1所示。采样频率1000 Hz。

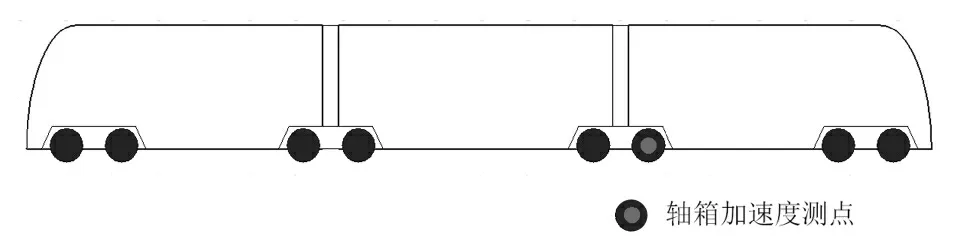
图1 有轨电车编组及轴箱加速度测点布置

有轨电车运行试验工况为AW0空载，运行速度为40 km/h。运行途中某段异常振动区间的轴箱垂向加速度数据如图2所示。由加速度图像可以看出该区段行驶时有一些明显的冲击位置，相应地引起有轨电车的异常振动。

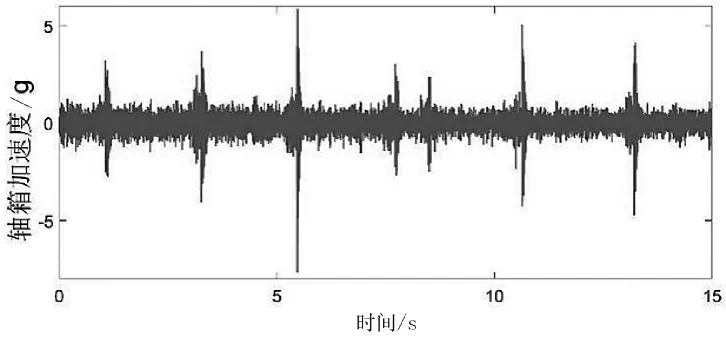
图2 试验全程轴箱垂向加速度

采用铁路接头平顺性评判方法对振动数据进行初步研究。该区段接缝不良指数如图3所示。由图3可以看出，从1.7 s开始，大约每过2.3 s出现一次冲击，冲击位置的接缝不良指数远远超过合格值4。该区段铁轨采用有缝轨道，根据冲击点间隔初步判断冲击是由轨缝处不平顺引起的。异常振动的特征频率分析及原因分析见下文。

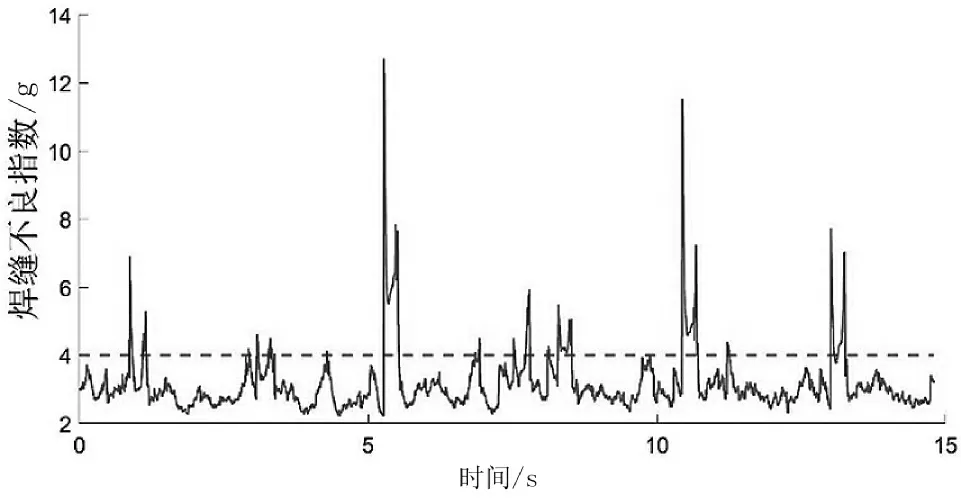
图3 接缝不良指数图像

3 异常振动信号EEMD与HHT分析

对异常振动信号的分析流程如图4所示。首先，对有轨电车轴箱的异常振动信号进行EEMD分解，得到各个IMF分量及其频谱图如图5所示。IMF1-IMF8是从高频到低频的IMF分量，RES为残余分量。

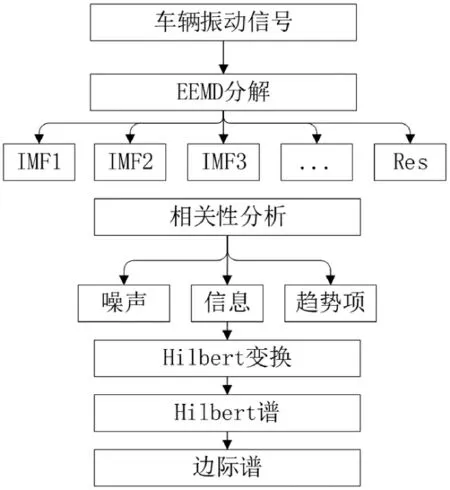
图4 算法流程

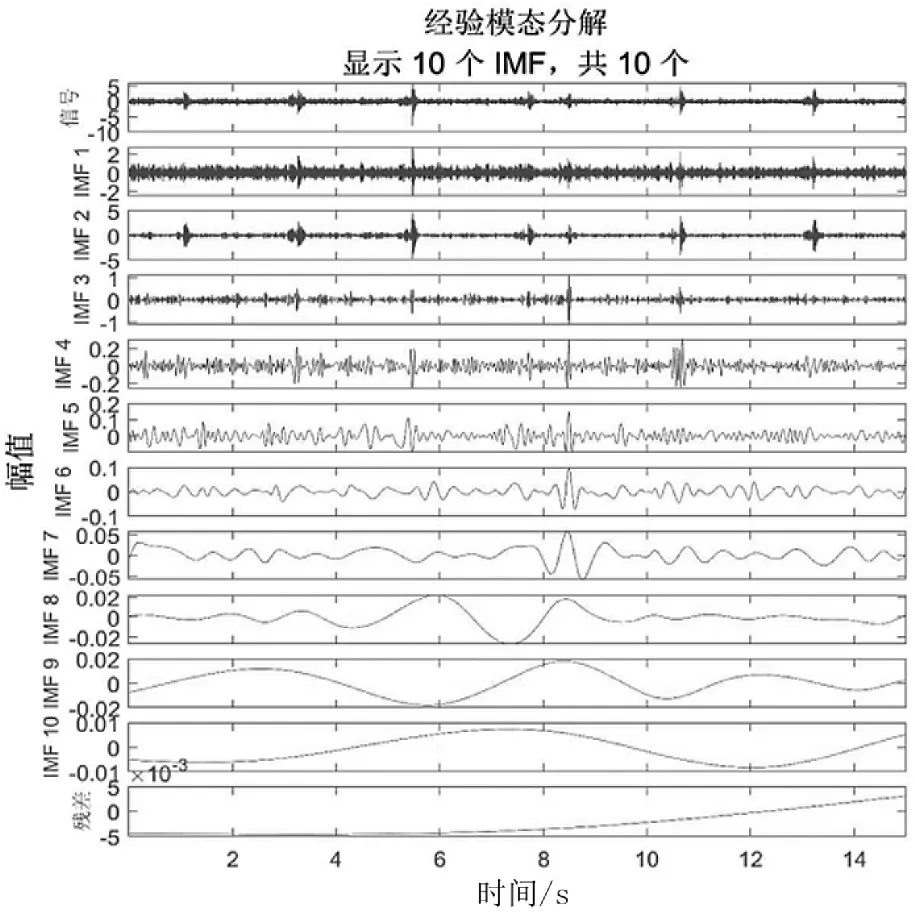
图5 异常振动信号EEMD各分量时域图与频域图

采用相关系数法计算各IMF与原始信号之间的相关系数，见表1，其中IMF1—IMF4的相关系数较高，并且是原始振动信号的主要成分，集中了原始信号中最显著的特征，对整体响应的影响最大；而IMF5—IMF8的相关系数均小于0.1，可认定为噪声分量或趋势量分量，对原信号的特征提取无意义，故剔除。

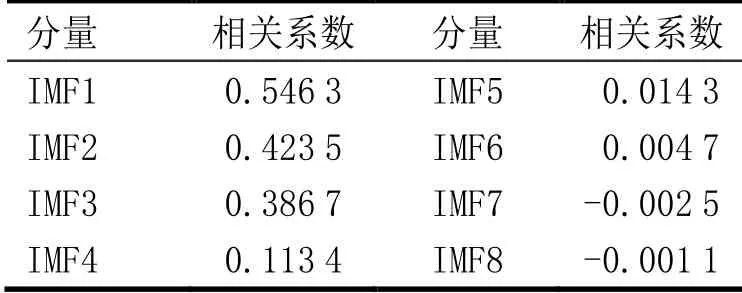
表1 异常振动信号各IMF与原始信号的相关系数

原始信号与由IMF1、IMF2、IMF3、IMF4组成的重构信号对比如图6所示。由图可见，原信号与去噪后的信号基本重合，原始信号的主要特征得以保留。

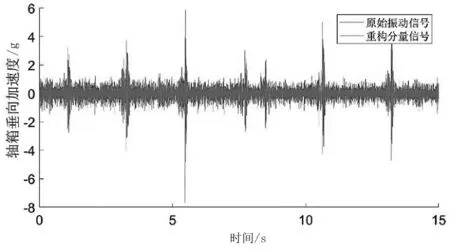
图6 原始信号与重构信号对比

对轴箱垂向振动信号的IMF1—IMF4分量进行瞬时处理，得到瞬时频率、瞬时相位及瞬时能量，进一步得到振动信号的Hilbert谱图，如图7所示。由图7可知，该信号能量几乎全部分散在0～150 Hz的宽频带中，频率高于450 Hz的部分几乎没有能量分布。其中50～100 Hz频带内的能量较大，其他频段能量比较弱。在1.1、3.3、5.5、8.5、10.7、13.25 s前后在50～100 Hz频带能量出现集中放大现象，瞬时能量远大于其他时段的瞬时能量。振动全程中存在4处明显的冲击。

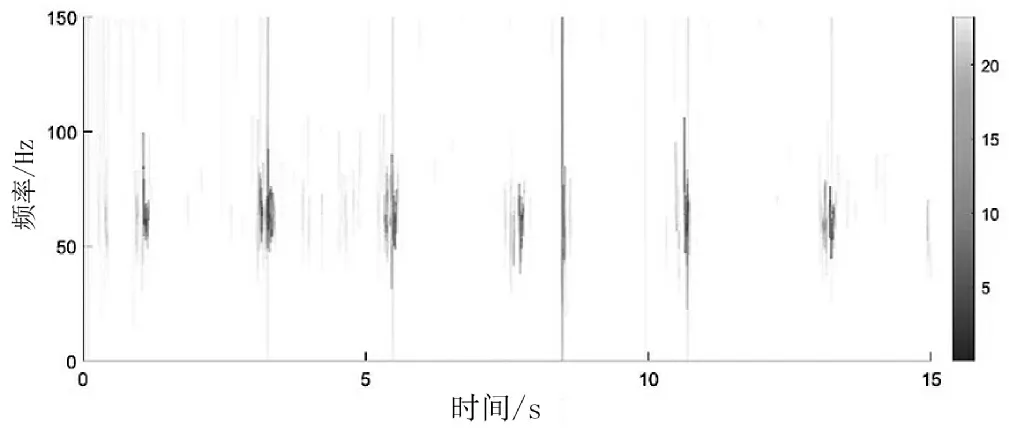
图7振动信号的Hilbert谱

图8 直观地展示了振动信号的时间-瞬时频率-瞬时能量的三维关系，由图8可知，该区段的振动信号存在6处冲击，且冲击间隔平均在2.2 s左右，且冲击能量逐次增强，在5.5 s，70 Hz达到能量最高点，最高瞬时能量为21.87。

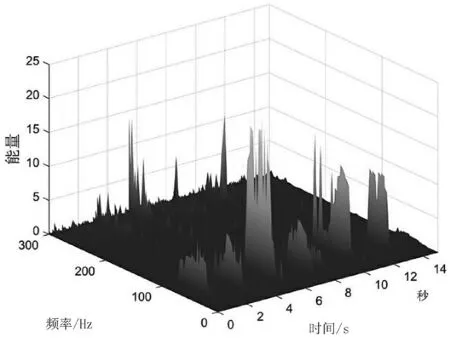
图8 时间-瞬时频率-瞬时能量图像

选取上述振动信号的5.4～5.6 s的冲击区段和5.8～6.0 s的平稳区段进行希尔伯特-黄变换，并通过HHT后的任意瞬时频率对时间的积分，得到异冲击区段和平稳区段的边际谱，用以表示信号各瞬时频率的总幅值的大小，如图9所示。由图9可知，冲击区段信号的能量主要分布在60 Hz附近的低频区域，信号的主振幅为0.0704，高频区域总的振动量较小。平稳区段信号的能量同样是主要分布在60 Hz附近的低频区域，信号的主振幅为0.0278。

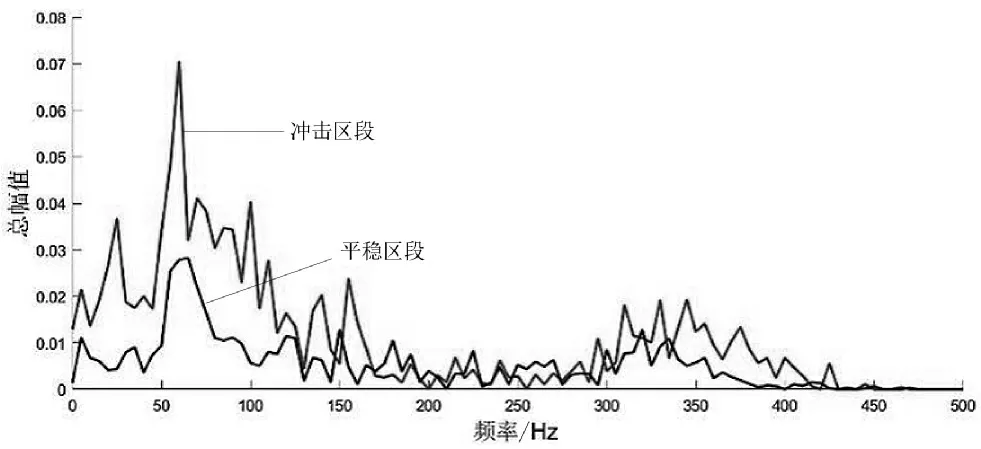
图9 振动信号的边际谱

4 轨道线路勘察

该段线路采用25 m标准钢轨，各段钢轨之间的轨缝较宽。在该异常振动区段的轨缝处，轨道连接板较高，导致有轨电车经过时钢轮与轨道连接板的顶面产生冲击。该速度下，约2.25 s经过一次轨缝并产生一次冲击，造成短暂时段内的异常振动。由上节HHT结果可知，车轮与轨道连接板顶面的冲击激发了有轨电车与轨道的共振，共振频率为60 Hz，冲击区段产生很大的瞬时能量。图10显示了冲击处轨道连接板的磨损光带。

图10 轨道连接板的顶面冲击

5 结论

本文采用HHT进行有轨电车异常振动分析。得到了以下结论。

（1）当有轨电车发生异常振动时，其振动信号的Hilbert谱与正常振动是不同的，可以利用振动信号的Hilbert谱来进行有轨电车异常振动分析及故障诊断。

（2）边际谱可以反映有轨电车振动信号中各个频率与总幅值的关系，明显区分出异常振动与正常振动，找到异常振动的真实频率值，通过异常频率成分对有轨电车进行故障诊断。