履带起重机支重轮-履带板接触问题分析

郑夕健，孟详佳

(沈阳建筑大学机械工程学院，辽宁 沈阳 110168)

随着社会的不断发展，人们的生活需求增高，各种建筑拔地而起，在建筑施工过程中都离不开工程机械，而其中履带起重机更是必不可少[1-2]。支重轮和履带板是其重要组成部分，两者间因接触造成的失效问题不在少数。因此，探讨轮板的接触强度，载荷变化规律对实际工作有一定的参考价值。

国外对于接触问题方面的研究成果众多：如P.L.Li等[3]利用有限元分析确定了可变形椭球体和刚性光滑平板间微接触引起的弹塑性变形状态；S.Zhang等[4]通过ANSYS Workbench软件建立了角接触轴承的模型，计算其接触应力。国内学者的研究方向大多数关于高速轻载方面，而针对履带起重机下车接触问题的相关研究较少。吴联朋等[5]通过Hertz理论分析履带起重机回转系统的弹性接触应力，改变材料属性，观察其弹塑性接触应力的变化；郑夕健等[6]针对大型擦窗机行走机构进行研究，运用有限元分析轮板模型弹性和弹塑性时接触状态，最后对承重轮进行优化设计。

基于上述为分析，笔者通过计算履带起重机履带接地比压以及支重轮的受载情况，依据Hertz理论计算支重轮和履带板间弹性阶段的接触应力，再运用有限元探究轮板结构的弹性和弹塑性的状态；与通过Hertz理论求得的结果进行比较，并验证有限元分析的准确性。

1 支重轮和履带板接触应力理论计算

1.1 履带接地比压和支重轮受力计算

履带接地比压是履带起重机的一个很重要的技术参数，履带起重机下车接地比压可以用梯形分布的公式计算；上车为非对称结构，起重机臂与x轴夹角为α，力学模型如图1所示。

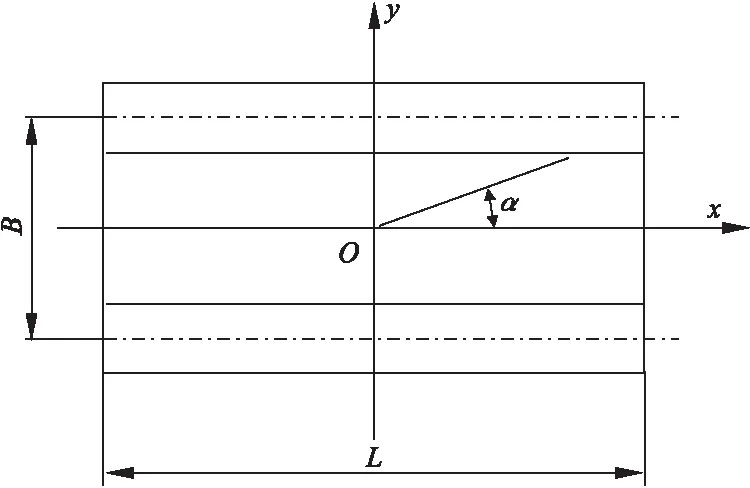
图1 起重机臂架转动示意图

当起重机臂架在车体正前方时，支重轮受载最大，整机的横向偏心距C=0，此时两条履带的接地比压分布形式及数值完全相同，即G1=G2=G/2。其中，G为机器的工作重力与垂直外载荷所构成的合力。

下车接地比压为

(1)

式中：Gx为下车整体的重力，N；L为履带和地面接触长度，m；b为履带和地面接触的宽度，m。

考虑上车结构，其重力在驱动轮端的接地比压为

(2)

只考虑上车重力时导向轮端点接地比压为

(3)

式中：Gs为上车整体重力，N；e为整机纵向偏心距，m；W为履带的接地平面的模量，m3。

(4)

(5)

将式(4)带入式(2)、式(3)可得：

(6)

履带接地比压的分布形式为梯形比压和三角形比压，L′为履带接地长度，如图2所示。图中数字1处代表驱动轮，数字10代表导向轮，两者连线与平面形成的夹角为α，支重轮1和2、支重轮2和3、支重轮3和4、支重轮4和5、支重轮5和6，每相邻2个支重轮间形成梯形接地比压，需把梯形分解为矩形和三角形形式，然后再叠加计算。支重轮6和支重轮7之间的线段内，履带比压为三角形形式，直接计算。

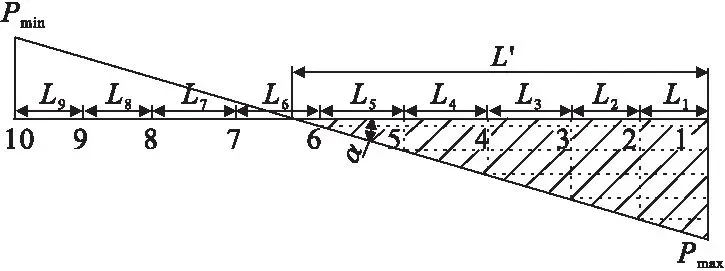
图2 履带比压分解示意图

把上车和下车者对驱动轮端1点产生的接地比压累加在一起，可得：

pmax=px+ps1.

(7)

叠加后履带架导向轮端10点处的比压为

pmin=px+ps2.

(8)

驱动轮和导向轮连线与地面之间形成的夹角为α正切值为

(9)

根据《履带起重机行走机构的结构分析》[7]的计算方法以及QUY80A履带起重机相关参数：下车重力GX=280 kN，上车重力Gs=1 575 kN，履带长度L=4 370 mm，履带宽度b=850 mm，纵向偏心距e=2 185 mm，L1=L2=L8=L9=430 mm，L3=L4=L5=L6=L7=530 mm，计算出支重轮受力大小如表1所示。

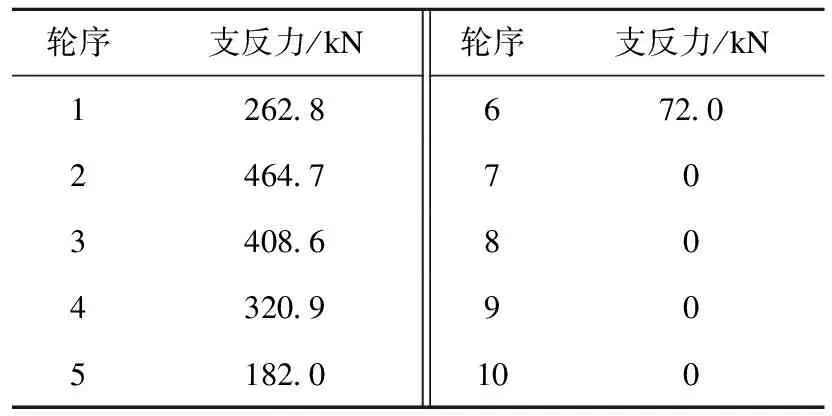
表1 支重轮支反力

从表中可以看出，支重轮2所受的支反力最大，为464.7 kN。

1.2 理论计算轮板接触应力

坐标原点选择为接触区域的中心，接着建立直角坐标系，z轴为垂直与接触面的方向，建立支重轮和履带板空间曲面方程。

z=z1+z2=Ax2+By2.

(10)

引用弹性半空间承受半椭球分布载荷作用下表面任意点位移公式[8]：

(11)

式中：q0为最大接触应力，Pa；a为椭圆长轴半径，m；b为椭圆短轴半径，m；μ为泊松比；E为弹性模量，Pa。

最终可得接触区域中心处最大接触应力表达式：

(12)

2 轮板接触问题有限元分析

履带起重机支重轮和履带板接触问题属于非线性问题，笔者利用ANSYS Workbench软件对轮板结构接触应力进行弹性和弹塑性分析。

2.1 轮板接触模型建立

参考规范《起重机车轮》(JB/T 6392—200[9]，支重轮材料选用ZG35Mn，履带板材料选用ZG35SiMn钢[10]。分析过程不考虑由于风载荷造成的侧向力，轮板结构如图3所示。取支重轮外径D=290 mm，轴径d=105 mm，支重轮节距L=200 mm，履带板高度H=92 mm，履带板上表面接触宽度B1=220 mm，履带板下表面宽度B2=85 mm。轮板接触模型如图4所示。

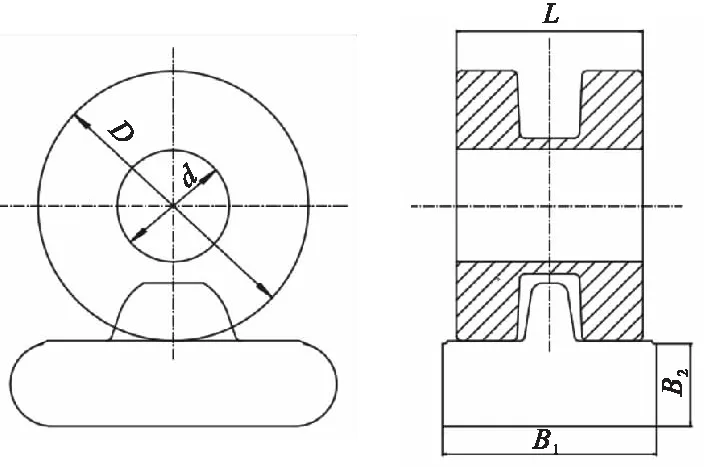
图3 轮板结构简图

图4 轮板有限元分析实体模型

2.2 设置接触条件和施加载荷

支重轮和履带板两者形成接触对，接触条件的设置方式是接触面定义为支重轮，目标面定义为履带板[11-12]。

根据之前的轮板理论求解方法，求得支重轮所受最大载荷Fmax=464.7 kN，以及根据赫兹公式求得理论最大接触应力σmax=1 345.03 MPa。

2.3 支重轮-履带板弹性接触

假定履带起重机轮板结构接触应力没有超过其材料的屈服极限，无塑性形变，即为弹性接触[13]。

支重轮和履带板的接触斑情况如图5、图6所示。由图可知，支重轮的最大等效应力为800.02 MPa，履带板的最大等效应力为593.36 MPa，履带板受到支重轮和履带板的接触斑均为椭圆形，履带板的应力扩散的面积比支重轮要大。

图5 支重轮接触斑

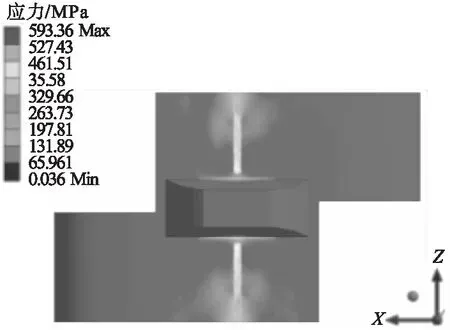
图6 履带板接触斑

轮板结构弹性接触状态整体分析后，得到两者接触应力最大值，如图7所示，其最大值为1 477.8 MPa。

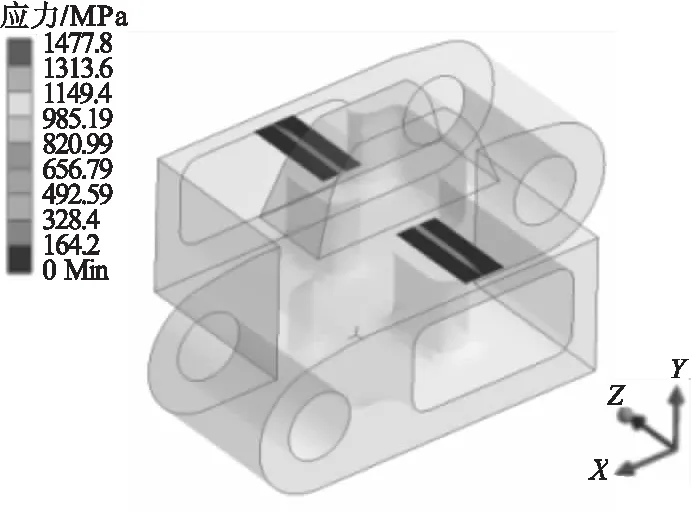
图7 轮板弹性接触应力

理论计算支重轮和履带板弹性接触应力最大值为σmax=1 345.03 MPa。运用有限元软件获得轮板间接触应力与之相差9.9%，两者结果如表2所示。有限元分析结果更符合实际状况[14-16]。

表2 轮板弹性分析结果与赫兹理论计算结果对比

2.4 支重轮-履带板接触弹塑性分析

在对轮板结构进行弹性分析时，并不能确定在何时出现塑性接触变形，支重轮和履带板某些接触区域上的接触应力超过其材料的屈服强度时，会释放部分材料应力，此时，接触应力会大幅降低。为了更加准确的获得支重轮和履带板发生塑性变形区域的接触应力，有必要对其进行弹塑性分析。

通过对支重轮和履带板材料特性设置，可以得到两者在弹性阶段和塑性阶段的应力-应变曲线(见图8、图9)。图中第一段折线代表轮板材料处于弹性接触时的变化，弹性模量E为折线斜率;第二段折线代表轮板材料处于塑性接触时的变化，此时已达到材料屈服极限，斜率代表材料强化模量Ep。

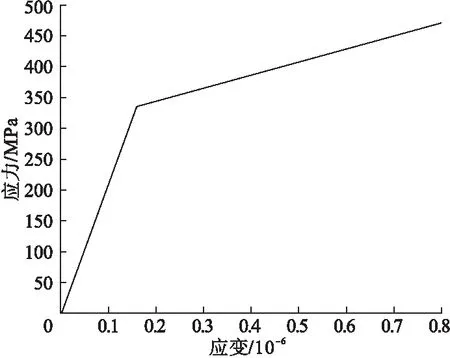
图8 支重轮BISO模型应力-应变关系曲线

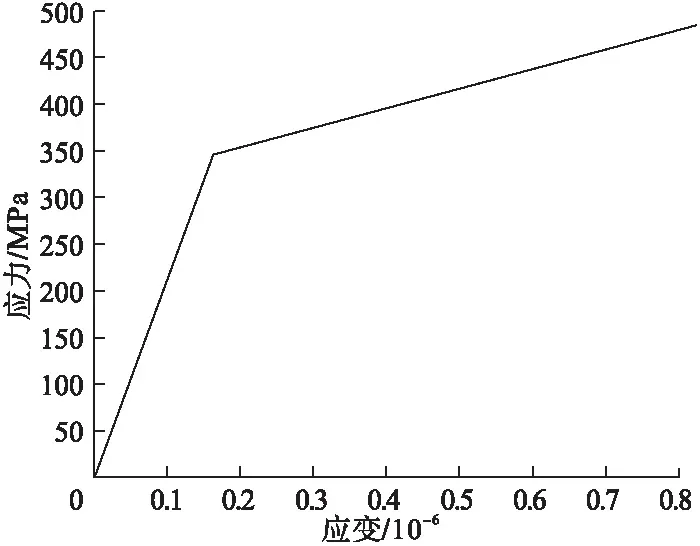
图9 履带板BISO模型应力-应变关系曲线

由图可以看出，在弹性阶段支重轮和履带板应力比应变的值大于塑性阶段，两条阶段的交点的纵坐标即表示材料的屈服强度。

对轮板结构弹塑性接触状态分析，分析方法和弹性阶段类似，最终得到支重轮和履带板接触过程中的最大Von-Mises等效应力分别为400.67 MPa和359.93 MPa。对比于弹性分析，弹塑性分析的Mises应力值明显降低，说明支重轮与履带板在接触过程中已经发生了塑性变形(见图10、图11)。

图10 弹塑性分析支重轮接触斑

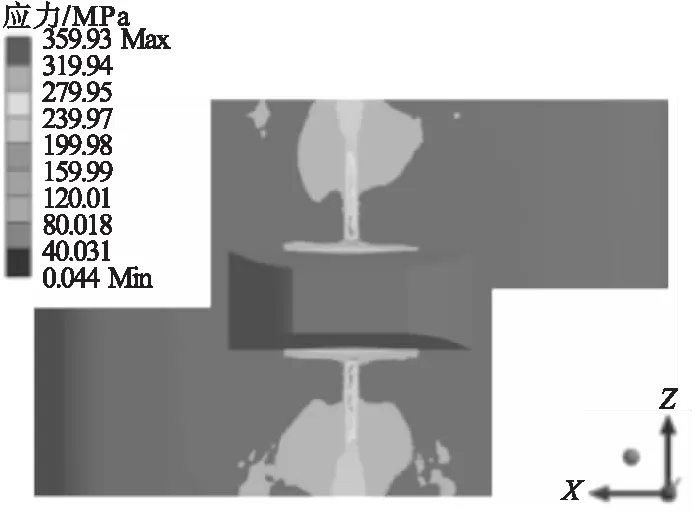
图11 弹塑性分析履带板接触斑

轮板弹性接触状态和弹塑性接触状态下其等效应力图如图12、图13所示。由图可知，在结构发生塑性变形后，其接触区域面积明显扩大，但接触应力值显著下降。

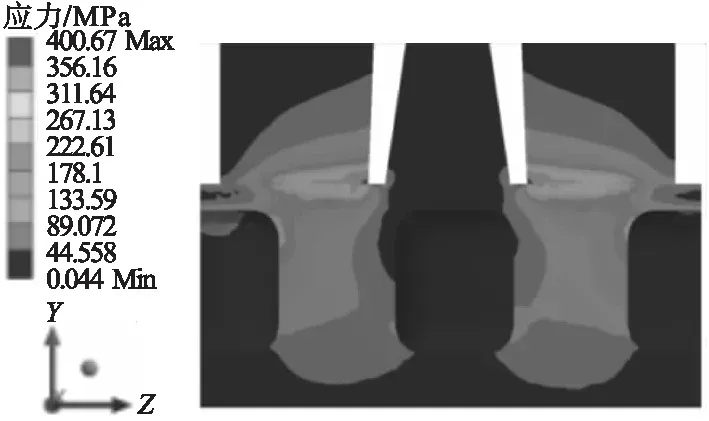
图12 弹塑性分析横向截面Mises应力云图

图13 弹塑性分析纵向截面Mises应力云图

轮板弹塑性接触应力为1 062.2 MPa，如图14所示。弹塑性阶段接触应力和弹性阶段接触应力对比值如表3所示。当同一载荷条件下，轮板结构弹塑性接触状态下的应力一定小于弹性接触状态下的应力。由表3可知，轮板结构在弹塑性阶段接触应力对比弹性阶段下降28.1%。

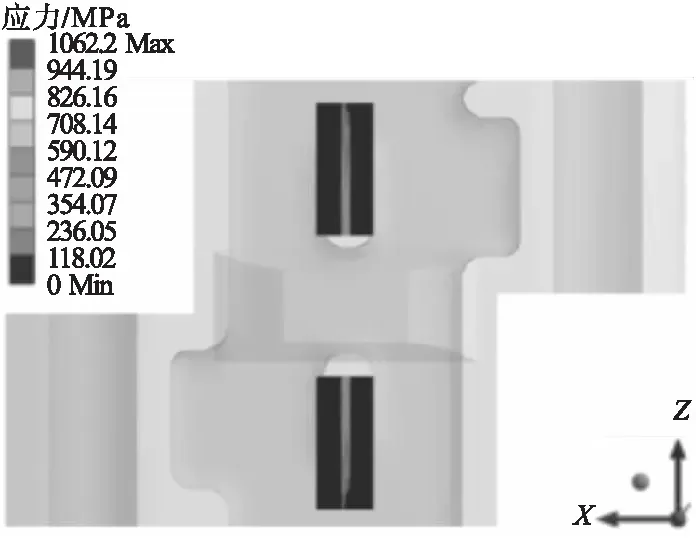
图14 轮板弹塑性分析接触应力

表3 轮板弹性分析与弹塑性分析结果对比

3 结 论

(1)通过利用ANSYS有限元分析软件，对履带起重机的支重轮与履带板弹性和弹塑性接触状态下接触应力的变化进行分析，获得了轮板结构两种接触状态下的最大接触应力值，弹性状态为1 477.8 MPa，弹塑性状态为1 062.2 MPa。

(2)针对轮板弹性接触状态，运用赫兹理论和有限元分析两种方法对比分析，获得的接触形状、接触应力和轮板结构应力基本相似；对其接触应力值的结果，有限元分析方式更为精确，赫兹理论假设条件过多，得到的数值结果偏大。

(3)在具有低速重载接触状态工程机械轮板结构中，由于实际工作情况比较复杂，载荷的变化也非常明显，难免出现过载的工况，长久以来，轮板结构会产生接触疲劳，所以使用合适的材料加工使其稳定的在弹塑性状态下，能有效避免结构破坏。