基于有限元方法的汽车座椅模态分析与优化
2022-11-15王克飞彭闪闪
王克飞,彭闪闪,李 龙
(安徽信息工程学院 机械工程学院,安徽 芜湖 241000)
0 引言
随着科技的进步和生活品质的提高,在汽车使用过程中,消费者越来越关注汽车NVH 性能,整车NVH 性能可通过控制各子系统NVH 来保证。 座椅是十分重要的汽车部件,其主要作用是为驾乘人员提供方便操作、舒适和安全的驾乘座位[1],汽车激励源的振动最终经过座椅传递到人体,会对汽车NVH 性能产生不利影响。 因此,开展座椅模态性能分析,降低其对汽车NVH 性能的影响十分重要。
李雪城等[2]采用有限元方法和试验方法获取了座椅初始模态参数,通过筛选敏感零件作为设计变量,对座椅模态进行了优化,避开了车身共振频率。 杨文彪等[3]基于具有可信度的座椅骨架有限元模型,研究了蛇簧对座椅模态的影响,提出考虑蛇簧预紧力的模型与试验结果更接近。 李玉光等[4]利用有限元软件对座椅骨架模态进行了分析,获得其前十阶模态参数,并将模态频率与人体器官的频率进行了对比并给出座椅模态频率设定的建议。 苏仕见等[5]通过灵敏度分析、拉丁超立方抽样,构造出座椅模态响应面模型,成功应用于座椅模态优化和轻量化设计。
1 模态分析理论
模态分析是指将线性时不变运动微分方程组中的物理坐标转变为模态坐标,使方程组解耦,从而识别出系统的模态参数。 对一个线性时不变系统,其运动一般动力学方程为[6]:

式中:M—质量矩阵;C—阻尼矩阵;K—刚度矩阵;f(t)—载荷列阵;x(t)—加速度列阵;x(t)—速度列阵;x(t)—位移列阵;t—时间。
对(1)式进行傅里叶变换得到

对(2)式进行解耦,同时考虑到模态振型矩阵的正交性,解耦后的方程为:
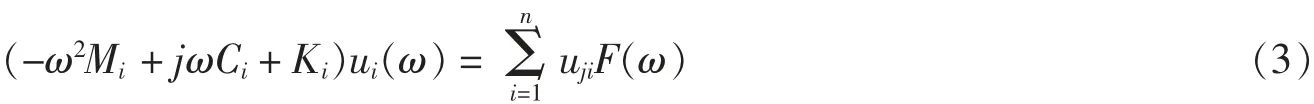
式中:u—模态振型矩阵。
式(3)即为有外部激励时n 阶运动系统第i 阶模态,通过对其求解可得到系统各阶模态参数,系统任意振动时刻的振型为各阶模态振型的线性组合。
由于模态是系统的固有特性, 与外部激励无关, 同时考虑到阻尼对结构的固有频率及振型影响较小,无阻尼自由振动方程为:

设方程的解为:

将解代入到方程(4),可得:

当系统自由振动时,必存在非零解使

式(7)即为无阻尼自由振动系统模态,通过对其求解可得到系统各阶模态参数。
2 座椅模态仿真分析
2.1 结构分析
待研究座椅主要由座垫组件、靠背组件、头枕组件、调节装置及装饰件等组成,其中,座垫组件由滑轨组件、地脚、边板、侧板、连接板、横杆、连杆及蛇簧等组成,靠背组件由管框、钢丝、曲簧、连接板等组成,头枕组件由头枕导管、头枕骨架等组成。 座椅连接关系复杂,其中,座垫组件通过调角器与靠背组件连接,靠背组件通过焊缝与头枕组件连接。座垫组件中滑轨组件通过螺栓与地脚、边板连接,边板通过螺栓与连杆下部连接,而连杆上部通过焊缝与横杆连接,横杆、连接板均通过焊缝与左右侧板连接。靠背组件中各零部件之间通过焊缝连接。头枕组件中头枕导管通过焊缝与头枕骨架连接。座椅结构及连接关系如图1 所示。 o-xyz 为整车坐标系。
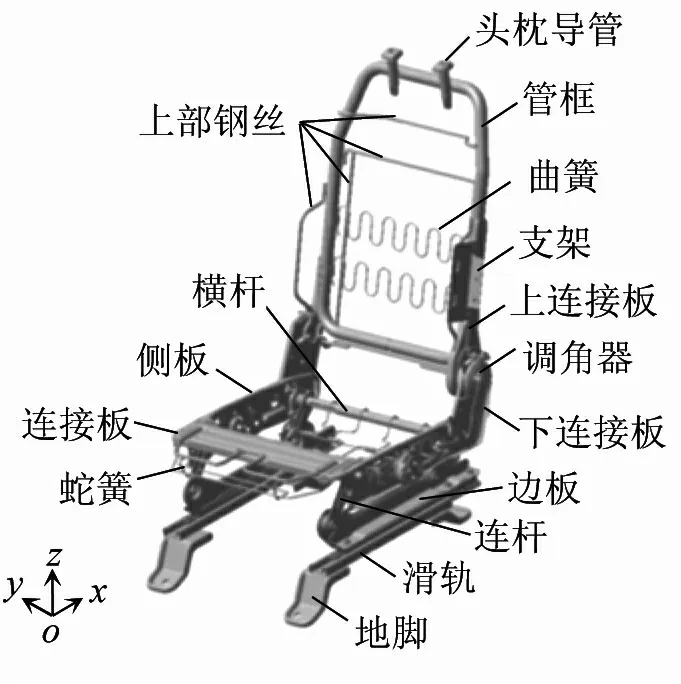
图1 座椅结构及连接关系图(装饰件隐藏)
2.2 仿真模型的建立
该座椅为管框钣金结构,可采用板壳单元对其建模。将座椅三维几何模型通过Hypermesh 软件专用接口进行导入,可利用Midsurface 功能抽取管框及钣金件中面,利用Quick edit 功能对中面进行几何清理,消除多余边及重复面,利用Automesh 功能划分壳单元网格,网格基本尺寸为5×5 mm,利用Qualityindex、Cleanup tools 功能对不满足质量要求的网格进行优化[7]。 网格划分过程中,为避免网格刚性过大,要以四边形单元为主,三角形单元为辅,最终共生成33 603 个单元,其中,四边形单元31 711 个,占比为94.4%。 对装饰件、钢丝、蛇簧等进行简化处理,采用非结构质量点单元Non-structure mass(Nsm)进行模拟,质量点的质量与简化件质量一致,并通过Rbe3 单元分配到连接件。
座椅连接关系中螺栓连接采用Bar 单元模拟,焊缝连接采用Rbe2 单元模拟。 座椅材料采用低碳钢参数进行定义,其中,弹性模量为210 000 MPa,泊松比为0.3,密度为7 850 kg/m3,各参数通过Material功能卡片进行赋值。 座椅零部件各单元类型要赋予对应单元属性,板壳单元类型为Pshell,单元厚度根据相应零部件实际厚度赋值。 Bar 单元属性为Pbar,截面参数按照相应零部件截面进行定义。 质量点单元Nsm 属性为Conm2,质量等于简化零部件结构的质量。 Rbe2 和Rbe3 单元不定义单元属性,各单元类型通过Property 功能卡片进行定义。 建立的座椅有限元模型如图2 所示。

图2 座椅有限元模型图
2.3 模态计算与结果分析
根据模态分析理论,无阻尼自由振动系统模态特性,可通过求解振动方程的特征值和特征向量来得到。 在OptiStruct 软件中,提供了跟踪法、变化法和兰索士法等多种特征值求解方法,其中兰索士法是基于跟踪法和变化法的改进算法,对求解稀疏矩阵特征值非常有效。 因此,座椅模态求解算法选用兰索士法,模态计算频率范围设为0.1~30 Hz,可通过EIGRL 功能卡片进行设定。 此外,还需建立约束和载荷步,首先利用Loadcol 功能卡片建立约束集,并通过Constraints 功能卡片约束座椅地脚螺栓孔全部自由度,再通过Loadstep 功能卡片建立载荷步,设定分析类型、约束方式、模态求解算法和输出位移等。 将模型提交求解器进行计算,计算结果如图3 所示。
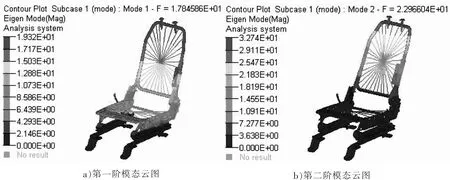
图3 座椅模态云图
由图3 可知,座椅第一阶模态频率为17.85 Hz,对应的第一阶模态振型为Y 向摆动。 座椅第二阶模态频率为22.97 Hz,对应的第二阶模态振型为X 向弯曲。
通过对座椅进行模态性能分析,获取模态特性,可评估其有无共振风险。其中,座椅模态特性设定的首要原则是座椅的固有频率不与发动机怠速频率发生共振。 而汽车发动机激励频率为[8]:

式中:n为转速,i为气缸数,τ为冲程系数(二冲程发动机τ取1,四冲程发动机τ取2)。
该汽车装载的发动机为四缸四冲程发动机,发动机怠速转速范围在650~750 r/min,由公式(8)可以算出,发动机怠速频率范围为21.67~25 Hz,该座椅第二阶固有频率落在发动机怠速频率范围之内,有共振风险,需对座椅进行优化。
3 座椅优化分析
3.1 优化方案
根据前述分析,座椅模态频率的优化目标可初定为小于21.67 Hz或大于25 Hz,但考虑到有限元模型误差、计算误差及试验误差等的影响,工程上常将共振频率范围向下、向上分别拓宽拓宽1~3Hz,作为安全频率范围。 本文将共振频率向下拓展1.67 Hz,向上拓展1 Hz,作为座椅安全频率范围,所以,该座椅模态频率的优化目标可为小于20 Hz或大于26 Hz。 针对座椅第二阶模态频率处于发动机怠速区间存在共振风险问题,可通过提高座椅刚度来改善其模态特性。 为此,提出以下优化方案:方案1如图4所示,是加强上下连接板刚度,并通过增加厚度来实现,其厚度由原来的1.5 mm更改为3.0 mm。 方案2如图5所示,是改善连杆结构,通过在前后连杆增加翻边来保证。方案3如图6所示,是提高边板刚度及与滑轨连接的可靠性,通过添加加强筋、改善拐角处结构及增大底部长度来保证。 方案4,是方案1、2、3的组合,用以综合评估。
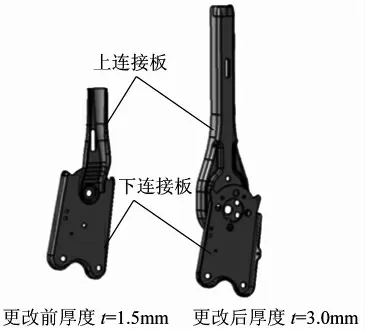
图4 方案1 示意图
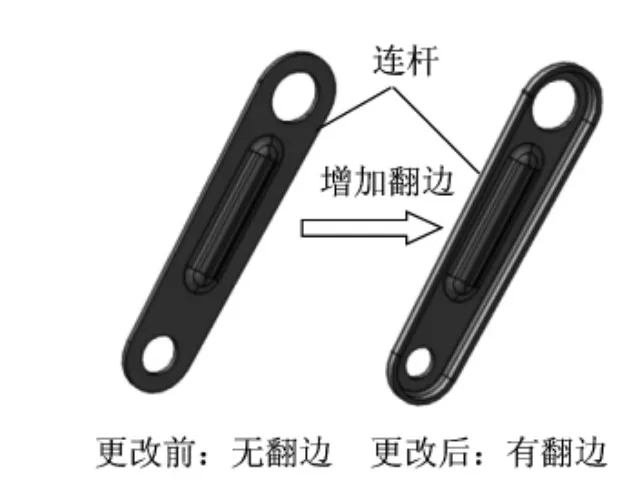
图5 方案2 示意图

图6 方案3 示意图
3.2 优化计算及结果分析
根据上述4 种优化方案,在有限元软件中分别建立相应的优化模型,并提交求解器计算。 计算结果如图 7~10 所示。
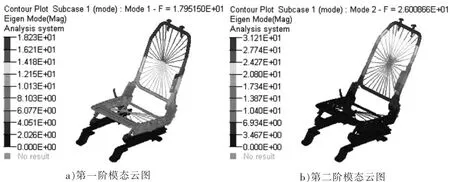
图7 方案1 优化结果图
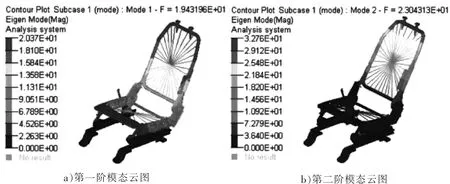
图8 方案2 优化结果图

图9 方案3 优化结果图
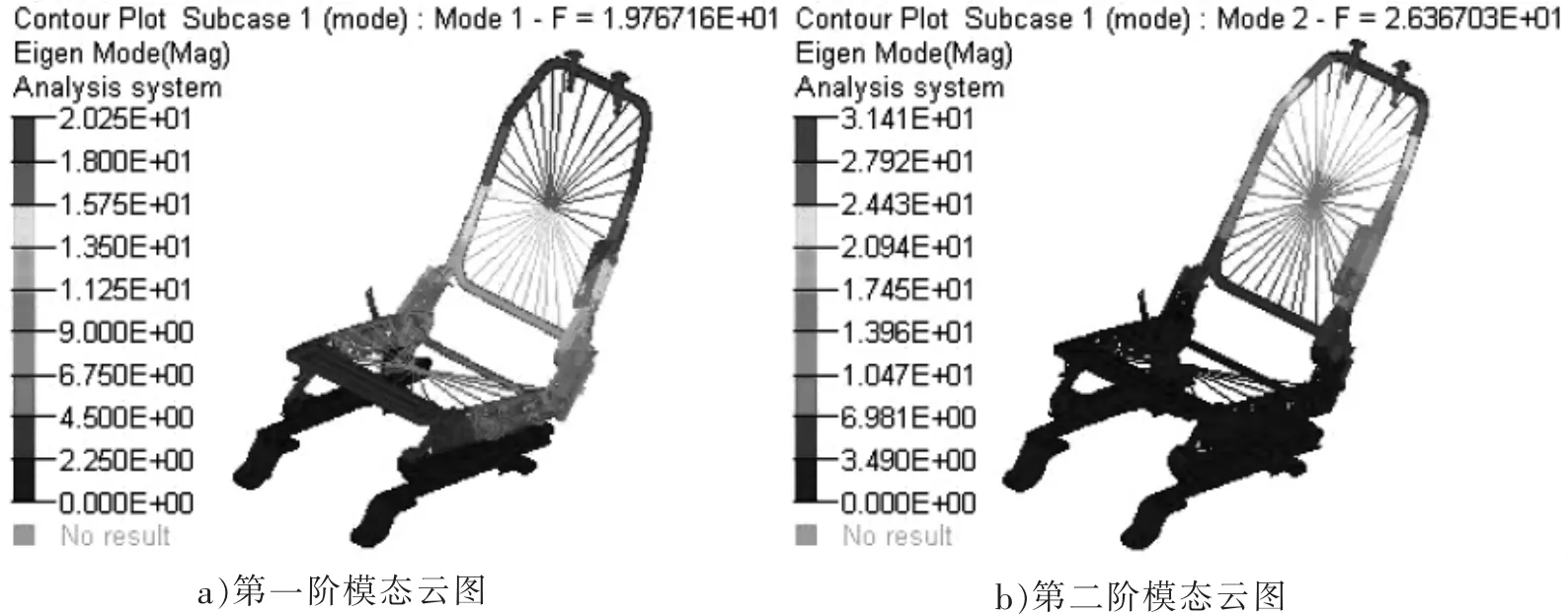
图10 方案4 优化结果图
从图7~10 中可以看出,振型方面,4 种优化方案第一阶模态振型均为Y 向摆动,第二阶振型均为X向弯曲,与原方案一致。模态频率方面,优化方案1、2、3、4 的第一阶模态频率分别为17.95 Hz、19.43 Hz、18.31 Hz、19.77 Hz,第二阶模态频率分别为 26.01 Hz、23.04 Hz、23.1 Hz、26.37 Hz。 由此可知,方案 1、4 满足座椅模态频率目标要求,而优化方案2、3 不满足座椅模态频率要求。 方案4,即将方案1、2、3 进行组合,能获得最好的座椅模态性能,但考虑到性价比,方案1 才是最佳方案。
4 种优化方案与原方案的模态参数对比如表1 所示。
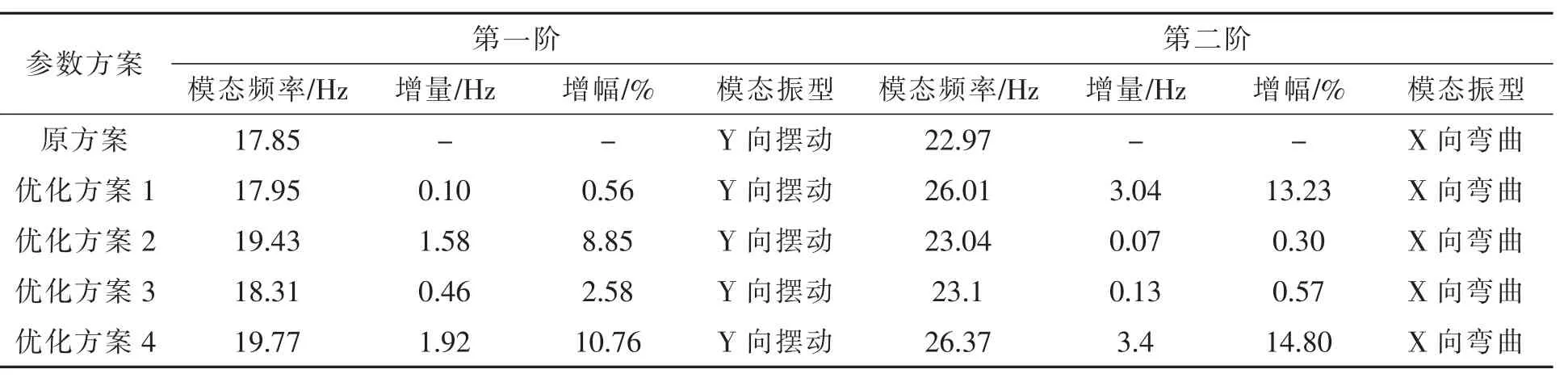
表1 4 种优化方案与原方案模态参数对比表
由表 1 可知, 优化方案 1、2、3、4 较原方案, 第一阶模态频率分别提高了 0.10 Hz、1.58 Hz、0.46 Hz、1.92 Hz,对应的增幅分别为0.56%、8.85%、2.58%、10.76%,而第二阶模态频率分别提高了3.04 Hz、0.07 Hz、0.13 Hz、3.40 Hz,对应的增幅分别为 13.23%、0.30%、0.57%、14.80%。 这说明除了组合方案 4 外,方案2 对第一阶模态频率提升最大,即通过改善连杆结构,可以有效提升座椅第一阶模态特性。 而方案1 对第二阶模态频率提升最大,即通过加强上下连接板刚度,可显著提升座椅第二阶模态特性。
4 结论
采用有限元方法探究了座椅模态性能,并根据发动机怠速频率,提出了座椅模态频率的优化目标,采用通过加强连接板刚度、改善连杆结构、提高边板刚度及与滑轨连接的可靠性和组合方案等4 种优化方案对座椅模态性能进行了优化,得出以下结论:
1)改善连杆结构,可以有效提升座椅第一阶模态特性,而加强上下连接板刚度,可以显著提升座椅第二阶模态特性,将两者组合,可获得更好的座椅综合模态特性。
2)较高的座椅模态频率可以有效避免与发动机怠速工况产生共振,座椅模态频率目标的设定需综合考虑发动机怠速工况、整车NVH 以及性价比。
