SCS-CN模型在济南市南部山区径流估算中的优化应用
2022-11-15赵登良陈振江刘建华孟凡荣徐征和桑国庆边振
赵登良,陈振江,刘建华,孟凡荣,徐征和,桑国庆,边振
(1.济南大学水利与环境学院,济南 250022;2.青岛市水利勘测设计研究院有限公司,济南 250013;3.山东济南市水文局,济南 250100;4.山东省水利厅,济南 250013)
地表径流是水文过程模拟的重要环节,是水量平衡的关键组成部分[1],地表径流的模拟为揭示人与自然因素共同作用下降雨-径流关系提供理论依据和科学方法[2]。在以水力侵蚀为主要类型的水土流失监测区,土壤侵蚀的过程是主要由降雨产生的径流对土壤的冲刷并带动土壤以泥沙的形式进行迁移[3]。因此,完整的水土流失监测技术不仅需要对土壤侵蚀进行测算,还需要在同尺度下对地表径流进行计算,这样才能明确水土流失的过程、掌握水土流失的规律、更科学地提出水土流失治理的方案。径流曲线模型(SCS-CN)是由美国于20世纪50年代提出的径流计算模型,其综合考虑了流域土壤类型、土地利用类型、前期土壤湿润程度与径流的耦合关系[4]。凭借着结构简单、所需参数简单的优势,该模型被广泛应用于国内外水文资料不足流域的径流预测[5]。卜慧等[6]将改进的SCS模型应用于老挝南乌河流域;彭云等[7]在内蒙古荒漠草原小流域对SCS模型进行了参数率定,并将该模型应用于区域山洪计算。不同区域SCS-CN模型的适用性需要进一步论证,其参数也需要根据研究区实际情况进行优化[8],因此本研究在济南市南部山区崮山流域进行该模型的参数优化研究,相关研究成果可以为济南市南部山区的生态保护、水土保持监测工作提供数据支撑,相关方法也可以为其他流域类似问题的研究提供参考。
1 材料与方法
1.1 研究区概况
崮山流域(以下简称研究区)位于济南市南部山区,覆盖张夏镇、万德街道和崮云湖街道的部分区域,流域总面积396.68 km2。研究区处于暖温带大陆性季风气候区,春季干旱少雨,夏季炎热多雨,地理坐标为东经116°48′36″~117°5′23″,北纬36°14′40″~36°31′47″[9]。研究区位置见图1。

图1 研究区位置
研究区位于泰山北麓,属于低山丘陵地区,地貌复杂,地势由东南向西北逐渐降低,海拔高度为120~920 m[10-11]。经查询《山东省土种志》,结合野外调查采集的土壤样品成分分析数据,确定了研究区土壤类型主要有褐土、棕壤、粗骨土、潮土4大类土壤,主要特征为土层浅薄,质地较粗,结构松散,砾石较多[12]。研究区的植被类型可以分为天然植被和人工植被两大类。天然植被主要以荆条、酸枣等灌木为主。人工植被主要是农作物和人工林:农作物以小麦、玉米、花生等为主;人工林则以侧柏、刺槐为主,还包括果园,以核桃、板栗为主[13]。
1.2 研究方法
1.2.1模型原理
SCS-CN模型假定集水区的实际入渗量与实际径流量之比等于集水区该场次降雨前的潜在入渗量即后损上限与潜在径流量之比,再之假定初损量与后损上限成比例[14],公式为
(1)
P=Ia+F+R
(2)
Ia=λS
(3)
式中:F为实际入渗量,mm;R为实际径流量,mm;S为潜在最大保持量,mm;P为降雨量,mm;Ia为初损,mm;λ为初损率。
由公式(1)、(2)、(3)联合求解可得:
(4)
由上式可看出集水区径流量取决于降雨量与该场次降雨前的潜在入渗量,而潜在入渗量又与区域土壤类型、土地利用类型、前期土壤湿润程度有关,SCS模型便通过其径流曲线数(CN值)来反映上述因素的影响,潜在入渗量也通过该参数经由下式计算:
(5)
在实际应用中,参考美国国家工程手册现行版本第九章的农业用地CN值选取表、城市地区的CN值选取表确定了本文所用到的标准SCS-CN模型AMCⅡ状态下的CN值表[15]见表1。

表1 崮山流域CN值取值
根据表2将土壤湿润程度按降雨发生前5日降雨总量划分为干旱(AMCⅠ)、正常(AMCⅡ)、湿润(AMCⅢ)3种状态,根据正常状态下的CN值计算其他两种状态下的CN值[16]:

表2 前期土壤湿润条件(AMC)划分
(6)
(7)
式中:CNⅠ、CNⅡ、CNⅢ分别代表干旱、正常、湿润状态下的CN值。
1.2.2模型优化
径流曲线模型(SCS-CN)作为在世界范围内广泛运用的径流计算模型,是由美国农业部土壤保持局的研究人员在进行了数万次的降雨产流试验后提出的[17]。该模型物理参数明确,当初损率λ固定为0.2时,无因次径流曲线数CN是其唯一的参数,这对于水文资料不全的监测区是非常适用的。但是,鉴于济南市南部山区处于石灰岩山地区且多是陡坡[18],将在小于5°的美国平原地区推演出的初损率λ和参数CN值直接套用理论上是不合适的[19]。故选取研究区2009—2018年内50次(M1~M50)降雨产流事件,对模型的初损率λ和参数CN值进行优化分析。研究区内5个雨量站和1个水文站是非均匀分布的,将站点坐标导入ArcGIS平台,对研究区2009—2019年的降水数据结合泰森多边形权重法进行筛选分析[20],根据前期土壤湿润条件(AMC)划分表规定的标准进行判断,研究所选的50次典型降雨中有23次为AMCⅠ、6次为AMCⅡ、21次为AMCⅢ。50次降雨和径流的分布关系见图2。

图2 50次典型降雨径流统计
2 结果与分析
2.1 模型优化分析
2.1.1标准SCS-CN模型计算
初损率λ取值为0.2,通过查表法获取研究区CN值分布栅格数据,计算M1~M50次降雨的径流深,计算值与实测值的优度拟合统计分析[21]见图3,回归直线的斜率为1.355,截距为3.615 4,确定系数R2为0.381 4,纳什效率系数ENS为-2.119 5。其中:在径流深范围处于0~0.5 mm时,模型计算结果大于实测值,有8次的计算结果大于5 mm;在径流深范围处于0.5~10 mm时,模型计算值小于实测值,有5次的径流深计算接近于0;在径流深大于10 mm时,模型仅有1次计算结果与实测值接近,其他均与实测值相差较大。

图3 标准SNS-CN模型计算径流深与实测径流深拟合结果
以上分析表明,标准SCS-CN模型在计算研究区径流深时误差较大,造成这种结果的主要原因是λ取值为0.2。已有相关研究[22]表明,鲁中南低山丘陵区λ取值范围在0.02~0.16时,ENS已超过0.5;王红艳等[23]利用SCS-CN模型估算黄土高原径流时也对λ值0.01~0.20的取值进行了率定,其结果表明,当λ取0.01时,模型ENS最大值为0.516。由此可见,对λ值的率定是非常必要的。
2.1.2Woodward模型计算径流
以Woodward为代表的研究人员针对径流曲线模型的适用性问题在美国进行的大量研究结果表明,λ取0.2并不适用于所有的流域,应根据流域的地域性特点对其取值。Woodward等[24]通过对美国的307个径流小区的研究得出了λ取0.05的模型效率要高于其取0.2,并推演出λ为0.05时CN值的转换模型为
(8)
使用Woodward改进的SCS-CN模型对M1~M50降雨事件进行径流深计算,并对计算径流深和实测径流深进行优度拟合分析,结果见图4。回归直线的斜率为1.745 5,截距为2.603 9,R2为0.590 6,ENS为0.435 5。与标准SCS-CN模型相比:该方法在径流深范围处于0~0.5 mm时,模型计算结果大于实测值,有9次的计算结果大于5 mm;在径流深范围处于0.5~10 mm时,计算值与实测值较为接近,但是有2次的径流深计算接近于0;在径流深大于10 mm时,模型仅有1次计算结果与实测值接近,其他均与实测值相差较大。
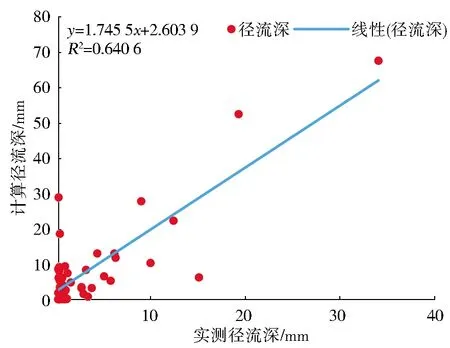
图4 Woodward模型计算径流深与实测径流深拟合结果
上述分析结果表明,在径流深处于0.5~10 mm时,Woodward法的计算径流深结果更接近实测值,在径流深处于其他范围时,该方法仍具有较大的误差。对于本研究选取的模型评价标准而言,该模型的效率整体上优于标准SCS-CN模型,为进一步提高模型的计算精度,继续对模型的参数进行优化。
2.1.3优化SCS-CN模型计算径流
继以上研究结果,首先对标准SCS-CN模型中的参数λ进行优化分析。在此分析过程中,将λ取值范围定为0~0.20,步长设置为0.01,CN值为标准SCS-CN模型中的查表值,不同λ取值的模型评价结果见图5。图5中,随着λ值的增大,回归直线的斜率呈逐渐减少的趋势,其取值范围为1.355 0~1.750 8;回归直线的截距呈先减少再增加的趋势,在λ为0.13时有最小值为2.591 7,在λ为0.01时有最大值5.678 3;优度拟合统计R2呈减少趋势,取值范围为0.381 4~0.442 5;ENS呈减少趋势,取值范围为-2.119 5~0.373 7,在λ≤0.06时,ENS取得正值。

图5 初损率λ优化分析结果
以上结果表明:在λ处于0~0.20时,模型的计算径流深整体上会大于实测径流深,随着λ取值增大,计算径流深有减小的趋势,但计算径流深和实测径流深的相关性也会降低,模型精确度也随之降低;λ取值越小,模型的精确度越高,尤其是在λ≤0.06时,模型的效率相对较高。
将CN值取查表值时,λ取值范围定在0~0.06一定程度上提高了模型的精度,可以作为λ取值的最优区间。但是模型的误差仍不可忽略,这是由于CN值的选取也会影响模型的计算精度,有研究表明地形因素对CN值的选取是不可忽略的,Huang等[25]在黄土高原陡坡区分析评价了标准径流曲线模型中边坡整合办法,并基于径流小区11年降雨径流数据提出了CN值的坡度修正公式见式(9)。

(9)
式中:CNα为修正后的CN值;α为百分比坡度。
考虑到Woodward模型中λ值为0.05正处于上述对λ率定的最优结果区间内,并且当λ取0.05时也有了较为成熟的CN值转换模型,因此接下来模型优化的方向是在Woodward模型的基础上引入CN值坡度修正模型。
基于ArcGIS平台,将研究区坡度图层、Woodward模型提取的CN值栅格图层(CNW)按照式(9)进行栅格运算,得到优化后的Woodward模型CN值(CNY)。在计算径流深前先对计算得出的50组CN值栅格数据进行加权平均计算,得出次降雨的研究区综合CN值,与基于实测降雨径流数据反推计算的CN值进行拟合分析,探讨优化CN值的适用性。
取λ为0.05,由式(3)、(4)、(5)可得:
CN=
(10)
基于M1~M50场次降雨的实测径流数据及降雨数据,利用式(10)计算出各次降雨的CN值,结合SPSS和Excel将优化后的CNY和反推法计算的CNF进行线性、多项式、对数、指数、乘幂拟合分析,其结果见表3。由表3可知,两组数据相关性较好,指数函数拟合时R2有最小值为0.662 8,多项式函数拟合R2有最大值为0.748 1。拟合分析表明CNY与CNF有较好的相关性,可以继续进行径流深计算。

表3 CNY与CNF拟合分析结果
使用参数优化后的SCS-CN模型对M1~M50场次降雨进行径流计算,并将计算结果按照不同的前期土壤湿润程度进行分类统计,对比3种方法计算径流深与实测径流深的分布关系,其结果见图6。

图6 不同方法计算径流深与实测径流深对比分析
在土壤前期湿度AMC Ⅰ状态下,分析每种模型的计算值与实测值的差值关系,其中:实测值与优化SCS-CN 模型计算值的误差均值为-0.02 mm,标准差为1.17;实测值与Woodward 模型计算值的误差均值为0.44,标准差为3.09;实测值与标准SCS-CN模型计算值的误差均值为2.54,标准差为5.63。实测值与优优化SCS-CN 模型的计算值误差最小且偏离程度小,与标准SCS-CN模型计算值相差最大,模型适用性排序为优化SCS-CN 模型>Woodward 模型>标准SCS-CN模型。
在土壤前期湿度AMC Ⅱ状态下:实测值与优化SCS-CN 模型计算值的误差均值为-0.32 mm,标准差为0.56;实测值与Woodward 模型计算值的误差均值为6.81,标准差为1.58;实测值与标准SCS-CN模型计算值的误差均值为2.19,标准差为3.77。实测值与优优化SCS-CN 模型的计算值误差最小且偏离程度小,与Woodward 模型计算值相差最大,模型适用性排序为优化SCS-CN模型>标准SCS-CN模型>Woodward 模型。
在土壤前期湿度AMC Ⅲ状态下:实测值与优化SCS-CN模型计算值的误差均值为0.70 mm,标准差为2.06;实测值与Woodward 模型计算值的误差均值为9.19,标准差为9.50;实测值与标准SCS-CN模型计算值的误差均值为7.73,标准差为14.42。实测值与优化SCS-CN 模型的计算值误差最小且偏离程度小,实测值与标准SCS-CN模型计算值的误差均值小于Woodward 模型,但是前者标准差小于后者,引入变异系数判断模型的适用性。实测值与Woodward 模型计算值的误差变异系数为1.03,与标准SCS-CN模型计算值的误差变异系数为1.86,因此模型适用性排序为优化SCS-CN 模型>Woodward 模型>标准SCS-CN模型。
为进一步验证参数优化后SCS-CN模型的效率,拟合分析实测径流深与优化SCS-CN 模型计算径流深,结果见图7。计算径流深与实测径流深的回归直线斜率为0.905 8,截距为0.544,R2为0.812 7,ENS为0.796 9。在径流深范围处于0~0.5 mm时,模型计算值略大于实测值,有两次超过5 mm;在径流深范围处于0.5~10 mm时,模型计算值与实测值接近,有3次的径流深计算接近于0;在径流深大于10 mm时,有3次计算结果均与实测值接近。
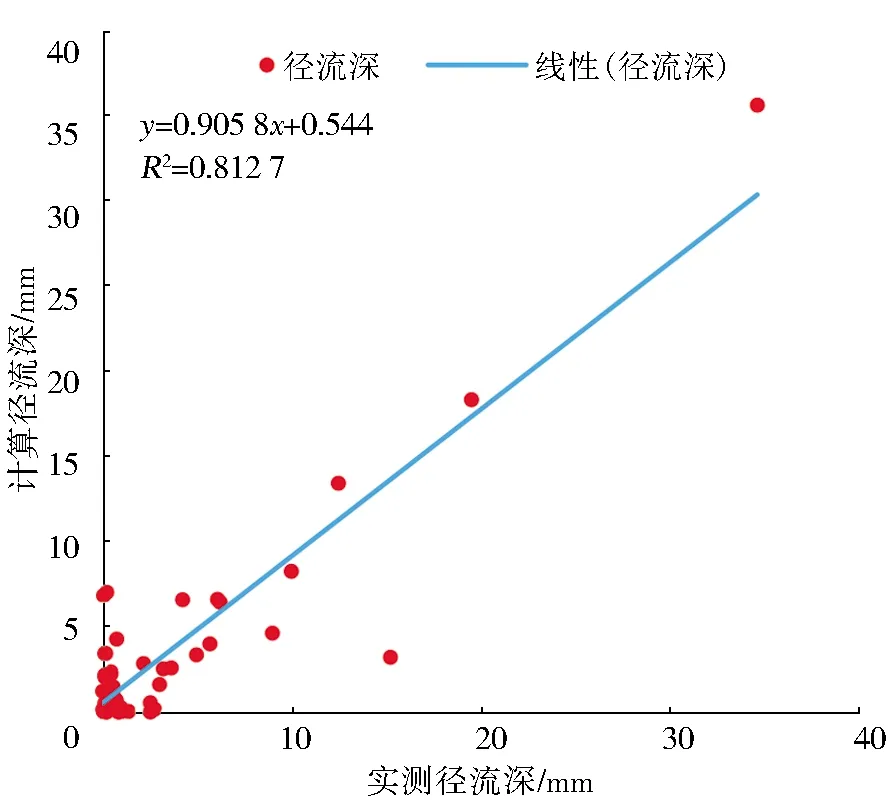
图7 优化SCS-CN模型计算径流深与实测径流深对比分析
2.2 研究区2019年径流量估算
对2019年降雨数据进行筛选,有29次降雨事件的降雨量超过侵蚀性降雨阈值(10 mm)按时间顺序编号为T1~T29,土壤前期湿润程度23次为AMC Ⅰ(T1~T7,T9~T18,T24~T29),1次AMC Ⅱ(T8),5次AMC Ⅲ(T19~T23)。使用优化后的径流曲线模型基于ArcGIS平台分别对29场次降雨进行径流计算,使用Zonal工具统计分析各降雨场次径流深计算的平均值,综合分析各降雨场次的降雨量和植被覆盖程度,其结果见图8。
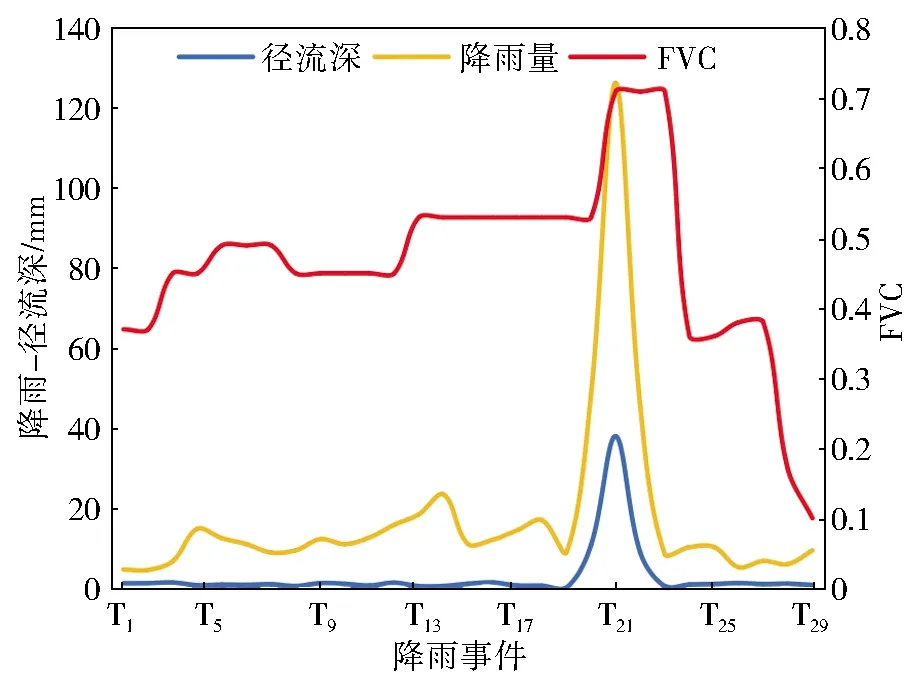
图8 29场降雨量、径流深及植被覆盖关系组合
由图8可以看出:T19~T23次降雨的径流量明显高于其他场次,表明在植被覆盖度相同的情况下,降雨量和土壤前期湿度对径流的产生影响较大;T1~T18及T24~T29场次降雨事件产生的径流量较小且变化不明显,径流深范围为0.08~1.39 mm,这表明在土壤前期湿度均为AMC Ⅰ的情况下,随着汛期的到来,降雨量的上升对径流深的变化影响不大,考虑是因为研究区植被覆盖程度在此期间呈现逐渐上升的趋势,且在汛期的中后期达到了全年植被覆盖度的最高值,植被截留降雨减小径流的作用随着植被覆盖度的上升而增加。
叠加29次径流深计算结果,得到2019年径流深分布栅格图见图9。可以看出,研究区年径流深呈南高北低,西高东低的空间分布特征,径流深范围在34.15~371.52 mm。结合ArcGIS中的分区统计工具计算得出研究区年径流量为0.53亿m3,年均径流深为134.52 mm,各镇年均径流深分别为:崮云湖街道93.52 mm,张夏镇92.36 mm,万德镇72.1 mm。
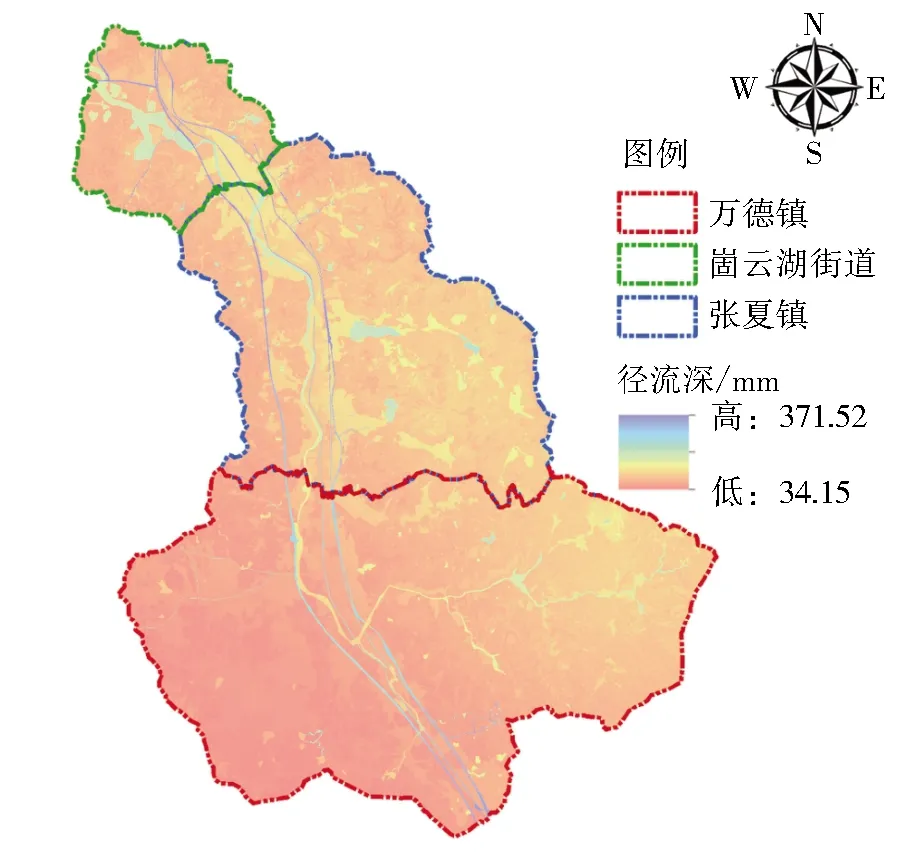
图9 崮山流域2019年年径流深分布
3 结 语
优化后的SCS-CN模型在研究区适用性较高,模型优度拟合确定系数较Woodward 模型提高了17.68%,较标准SCS-CN模型提高了113.08%;ENS较Woodward 模型提高了48.81%,较标准SCS-CN模型提高了137.59%。
研究区2019年各侵蚀性降雨场次产生的径流受到降雨量大小和植被覆盖情况等多方面因素影响,根据本文的研究成果可以判定降雨量与径流量呈正相关,植被覆盖程度与径流量呈负相关。
2019年崮山流域年径流量为0.53亿m3,空间分布上呈现北高南低、东高西低的分布规律,流域内各行政镇区年均径流深排序为崮云湖街道>张夏镇>万德镇。
模型优化过程中参数CN值的优化是在查表值的基础上得到,研究区的土壤类型及人工栽培的树种和自然树种等植被类型交错复杂,接下来研究计划通过建立径流小区并持续观测,以进一步优化SCS-CN模型的参数取值,提高其在济南市南部山区的应用精确度。
