基于双侧破坏模式的临坡地基承载力简化分析方法

彭文哲 陈玖颖 赵明华

摘要：为探讨临坡地基破坏模式，提出了相应的承载力计算方法.首先，考虑临坡地基各滑块几何尺寸和形状的非对称性，建立了临坡地基双侧破坏模型；其次，基于极限分析上限定理及虚功率方程，并引入强度发挥系数考虑远离坡面一侧的土体强度发挥程度，提出了临坡地基承载力的简化计算方法；最后，通过某工程实例的数值计算结果，验证了理论分析模型及计算方法的合理性，并通过不同工况下的对比结果，确定了强度发挥系数的合理取值.上述分析方法可考虑临坡地基破坏模式的双侧性，以及临坡距对地基承载力的影响，还可退化为平地地基承载力分析，为山区道路工程的设计计算提供了一定的参考，具有一定的理论及工程应用价值.

关键词：岩土工程；承载力；地基；双侧破坏模式；发挥系数

中图分类号：TU470文献标志码：A

Simplified Analysis Method of Bearing Capacity for Foundation Near Slope Crest Based on Bilateral Failure Mode

PENG Wenzhe，CHEN Jiuying，ZHAO Minghua

（College of Civil Engineering，Hunan University，Changsha 410082，China）

Abstract：This paper put forward the corresponding calculation method of bearing capacity to investigate the failure mode of the foundation near slope crest. Firstly，a model of bilateral failure mode for foundation near slope crest was established by considering the asymmetry of geometric size and shape of each slide block. Next，a simplified analysis method for the bearing capacity of the foundation adjacent to the slope was proposed based on the upper limit theorem of limit analysis and virtual power equation，and introducing the soil strength mobilization coefficient to characterize the strength mobilization of soil far from the slope. Then，the rationality of the theoretical analysis model and calculation method was verified by the numerical calculation results of an engineering example，and the reasonable value of the soil strength mobilization coefficient was determined by comparing the results under different working conditions. The aforementioned analysis method can consider the bilateral failure mode for the foundation near slope crest and the influence of the distance between the foundation and slope crest on the bearing capacity of the foundation. Meanwhile，it can also be degenerated to that for analyzing the bearing capacity of the ground foundation，which can provide a certain reference for the design and calculation of road engineering in mountainous areas，and has certain theoretical and engineering application value.

Key words：geotechnical engineering；bearing capacity；foundation；bilateral failure mode；mobilization coefficient

我国山区面积占国土面积的2/3，在公路和铁路等交通基础设施建设不断推进的过程中，时常会遇到在山区修筑路基的工况.边坡的存在将导致地基承载力大幅降低[1-2]，直接影响着山区道路工程的安全性和经济性，若因承载力不足引起滑坡、崩塌等重大事故，将导致巨大的生命和财产损失.现行规范尚无明确针对临坡地基承载力的计算方法，在实际工程中，或将其等效为平地地基处理，或依据工程经验对其承载力进行折减，导致计算结果可能偏于危险或过于保守.因此，探究临坡地基的承载力问题具有相当重要的工程意义.

目前，常用的地基承载力分析方法主要有极限平衡法、滑移线法和极限分析法等.其中，极限分析法在分析地基承载力时无须精确确定破坏机构内部的应力分布，适用于各类复杂岩土工程问题的求解. Meyerhof[3]在经典Terzaghi地基承载力公式的基础上，较早地提出了考虑边坡影响的临坡地基承载力计算方法；陈祖煜[1]建立了由对称主动区、过渡区和被动区三滑块组成的临坡地基单侧破坏模式，有效考虑了临坡距对临坡地基承载力的影响；王红雨等[2]基于极限平衡法，讨论了临坡地基滑移面的几何形状，提出了临坡地基滑移模式，进而推导出相应的承载力估算公式；杨峰等[4]假定临坡地基单侧滑块在破坏区域的过渡区内形成网格状滑块，进而引入优化变量，推导出地基承载力系数上限解；胡卫东等[5]深入分析临坡地基破坏机理，引进滑移线场理论，构建出考虑临坡地基破坏非对称性的单侧破坏模式，并基于极限分析上限定理，提出了临坡地基承载力计算方法.上述研究均采用单侧破坏模式，虽然考虑了临坡地基土體应力非对称引起的滑块非对称性，但一些临坡地基承载力试验[6-8]和数值模拟[9-15]研究表明，单侧破坏模式未能考虑远离坡面一侧的地基土体对地基承载力的贡献，其结果往往偏于保守.尉学勇等[16]基于极限平衡法和极限分析法，提出了可反映临坡地基破坏双侧性的破坏模式.在此基础上，胡卫东等建立了考虑临坡距的临坡地基承载力计算模型，分别采用极限平衡法[17]、极限分析法[18]和滑移线法[19]等对其进行分析，进而采用优化分析方法，提出了临坡地基承载力的计算方法.此外，蒋洋等[20]基于滑移线法，建立了斜坡地基破坏模型，并根据塑性边界条件，推导出无重土斜坡地基极限承载力解析公式，进而通过离心试验验证其合理性.然而，上述研究在考虑远离坡面一侧地基土的强度发挥时，计算过程过于繁琐.

鉴于此，本文将考虑临坡地基破坏模式的双侧性，基于极限分析上限定理，构造符合机动许可速度场的破坏机构，并引入强度发挥系数，表征远离坡面一侧地基土的强度发挥程度，进而通过某工程实例验证本文理论模型及计算方法的合理性，并提出强度发挥系数的合理取值，以期完善临坡地基承载力分析的理论与方法.

1临坡地基双侧破坏模式

由于单侧破坏模式未考虑远离坡面一侧地基土强度对其承载力的影响，故其计算结果可能相对保守，基于双侧破坏模式的承载力计算结果应更为贴近实际值.

为此，在现有研究成果的基础上，考虑临坡地基破坏模式的双侧性，建立了相应的破坏模式（图1）：

1）主动区非对称刚性滑块I，即路基荷载正下方的非对称三角形楔体ABC，其底角α（α=45°+φ2）和α_m（α_m=45°+φ_m/2）不相等，α_m随路基荷载、土体性质及边坡坡度等变化，φ_m的变化范围为φ_m∈[0，φ].

2）弹塑性过渡辐射剪切区滑块II和N，即三角形楔体ABC两侧的楔体BCD和ACG，滑块II和IV将分别沿滑移线CD和CG（对数螺旋线）向两侧发生滑动破坏，其楔体辐射区顶角分别为θ和θ_m，滑块II和IV的几何尺寸也能有效反映临坡地基破坏模式的非对称性.

3）被动区滑块III和V，即过渡辐射剪切区楔体BCD和ACG两侧的楔体BDEF和AGH，二者分别沿对数螺旋线CD和CG的切线方向发生平移滑动，形成连续滑动面，也表现出几何尺寸和形状的非对称性.

图1中L₁为路基荷载外边缘与坡面的距离，L₂为路基荷载内边缘到破坏线边缘的距离，L₁、L₂可分别表示为：

式中：a为临坡距系数.

鉴于极限分析上限解是一个关于多变量（α、α_m、θ和θ_m）的优化问题，并不便于工程设计人员直接应用和初步设计，故引入强度发挥系数m的概念，假定间断线ACGH上各点应力状态满足破坏准则f_m=0，如图2及式（3）所示.

综上，可构建出临坡地基双侧破坏模式，该模式较好地反映了地基沿两侧的滑动破坏及两侧滑块几

何尺寸和形状的非对称性，其分析模型主要受强度发挥系数控制.

2速度场分析

首先作出基本假定如下：

1）路基荷载正下方刚性滑块以速度v_p垂直向下运动；

2）主动区I、被动区III和V均为刚体；

3）过渡区II与IV均为理想塑性体，满足Mohr- Coulomb破坏准则与关联流动法则.

结合机动允许速度场和速度间断面的相容关系（图3），可推导出各速度间断面的速度.

由Mohr-Coulomb破坏准则和关联流动法则可知，间断面AC上各质点速度v₁与间断面AC之间的夹角为φ_m，v₁大小为：

间断面BC上各质点速度v₂与间断面BC之间的夹角为φ，v₂大小为：

射线BC上各质点速度v₃与间断面BC垂直，v₃大小为：

间断面CD上各质点速度v_CD的大小为：

v_CD=v₃e^θtanφ（7）

楔体BCD中，由射线BC至BD，间断面CD上各点的速度大小及方向都在改变，但其方向一直和间断面CD的切向成夹角φ，且垂直于经B点射线.其中，射线BD垂直于D点间断速度v₄，v₄大小为：

射线AC上各质点速度v₆与间断面AC垂直，v₆大小为：

间断面CG上各质点速度v_CG的大小为：

同样地，间断面CG上各点速度的方向和大小也在改变，速度方向一直同间断面CG的切向成夹角φ_m，并垂直于经A点射线.其中，G点间断速度v₇方向垂直于射线AG，v₇大小为：

假定滑块III速度为v₅，由于破坏面DE下方土体不发生运动，则速度间断面DE上真实间断速度为v₅.间断线BD上各点速度v₄与间断线BD垂直，v₄为间断面CD上的实际间断速度，和间断线CD在D点切向之间夹角为φ，滑动面ACDE为连续破坏面，对数螺旋线CD在D点的切线为DE，故v₄和v₅在方向上保持相同，v₅的方向也与BD线垂直.此外，v₅和v₄在間断线BD垂直方向上的分量一致，则速度v₅和v₄大小均可表示为：

综上，v₅与v₄大小相等，方向相同，面BD两侧的速度连续，并不是速度间断面，故无能量耗散发生.

同理，间断面GH真实的间断速度v₈和v₇大小相等，方向相同，故v₈与间断面GH之间的夹角为φ_m，v₈和v₇大小为：

面4G两侧的速度连续，并不是速度间断面，故无能量耗散发生.

3临坡地基承载力上限解

3.1外力功率

外力功率主要包括路基荷载Q_u的外力功率W_u及各滑块自重的外力功率W_I、W_II、W_III、W_IV和W_V.

路基荷载Q_n的外力功率W_n为：

W_u=Q_ubv_p（14）

滑块I和III自重外力功率W_I和W_III分别为：

W_I=γS_ABCv_p（15）

W_III=-γS_BDEFv₅cosβ（16）

式中：β=π-α-θ；β_m=π-α_m-θ_m；

滑块II与IV自重产生的外力功率W_II与W_IV分别为：

式中：

式中：γ为地基土重度；S_ABC和S_BDEF分别为滑块I与III的面积，可通过几何形状计算而得.于是，滑块I与III的自重外力功率W_I和W_III分别为：

滑块V自重外力功率W_V为：

W_V=-γS_AGHv₈cosβ_m（21）

式中：S_AGH为滑块V的面积，其大小为：

滑块V因自重引起的外力功率W_V亦可表示为：

于是，总外力功率W为：

W=W_u+W_I+W_II+W_III+W_IV+W_V（24）

3.2内能耗散率

内能耗散率主要包括速度间断面及楔体内部的能量耗散率，前者为间断速度与黏聚力c或c_m的点积，后者为塑性应变率与应力之积.

间断面AC上的能量耗散率D_AC为：

间断面BC上的能量耗散率D_BC为：

间断面DE上的能量耗散率D_DE为：

D_DE=cb（L₃+L₄）cos（α-φ）v_pe^θtanφ（27）

式中：

间断面GH上的能量耗散率D_GH为：

间断面CD和CG上的能量耗散率D_CD和D_CG分别为：

楔体BCD和ACG塑性能耗散率D_BCD和D_ACG分别为：

D_BCD=D_CD（31）

D_ACG=D_CG（32）

综上，内能耗散率总和D可表示为：

D=D_AC+D_BC+D_DE+D_GH+D_CD+D_CG+D_BCD+D_ACG（33）

3.3上限解

由极限分析上限定理可知，内能耗散率应与外力功率一致，则：

W=D（34）

整理可得Q_u的Terzaghi承载力形式如下：

式中：N_c和N_γ均為临坡地基承载力系数，分别受黏聚力c和重度γ控制.

N_c可通过与黏聚力c相关的能量耗散公式（25）～（32）推导，并通过合并同类项表示为f₇至f₁₁的函数.其中，f₇可通过联立式（25）和（26）推导，f₈、f₉、f₁₀和f₁₁可分别通过式（29）（30）（27）和（28）变换而得.

N_c=f₇+f₈+f₉+f₁₀+f₁₁（36）

式中：

N_γ可通过与重度γ相关的自重外力功率公式（17）～（20）和式（23）推导，并通过合并同类项表示为f₁₂至f₁₆的函数，f₁₂、f₁₃、f₁₄、f₁₅和f₁₆可分别通过式（17）（19）（20）（18）和（23）变换而得.

N_γ=f₁₂+f₁₃+f₁₄+f₁₅+f₁₆（37）

式中：

4工程实例

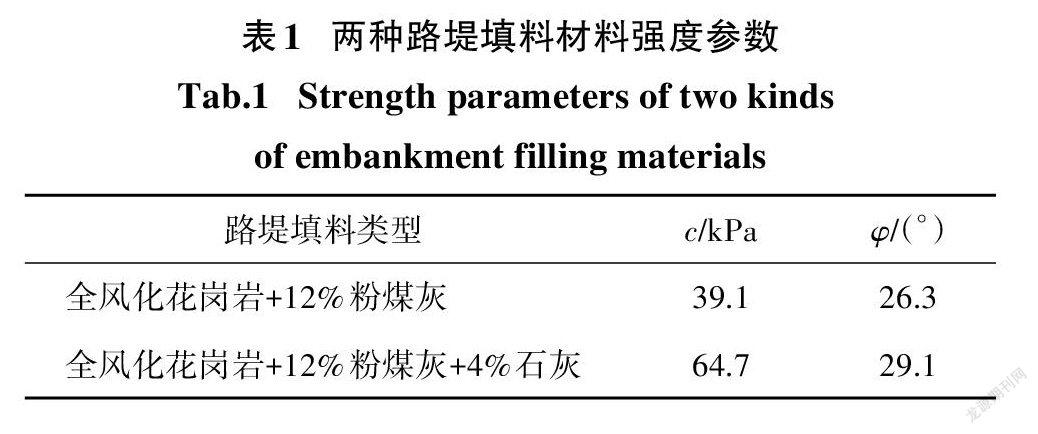
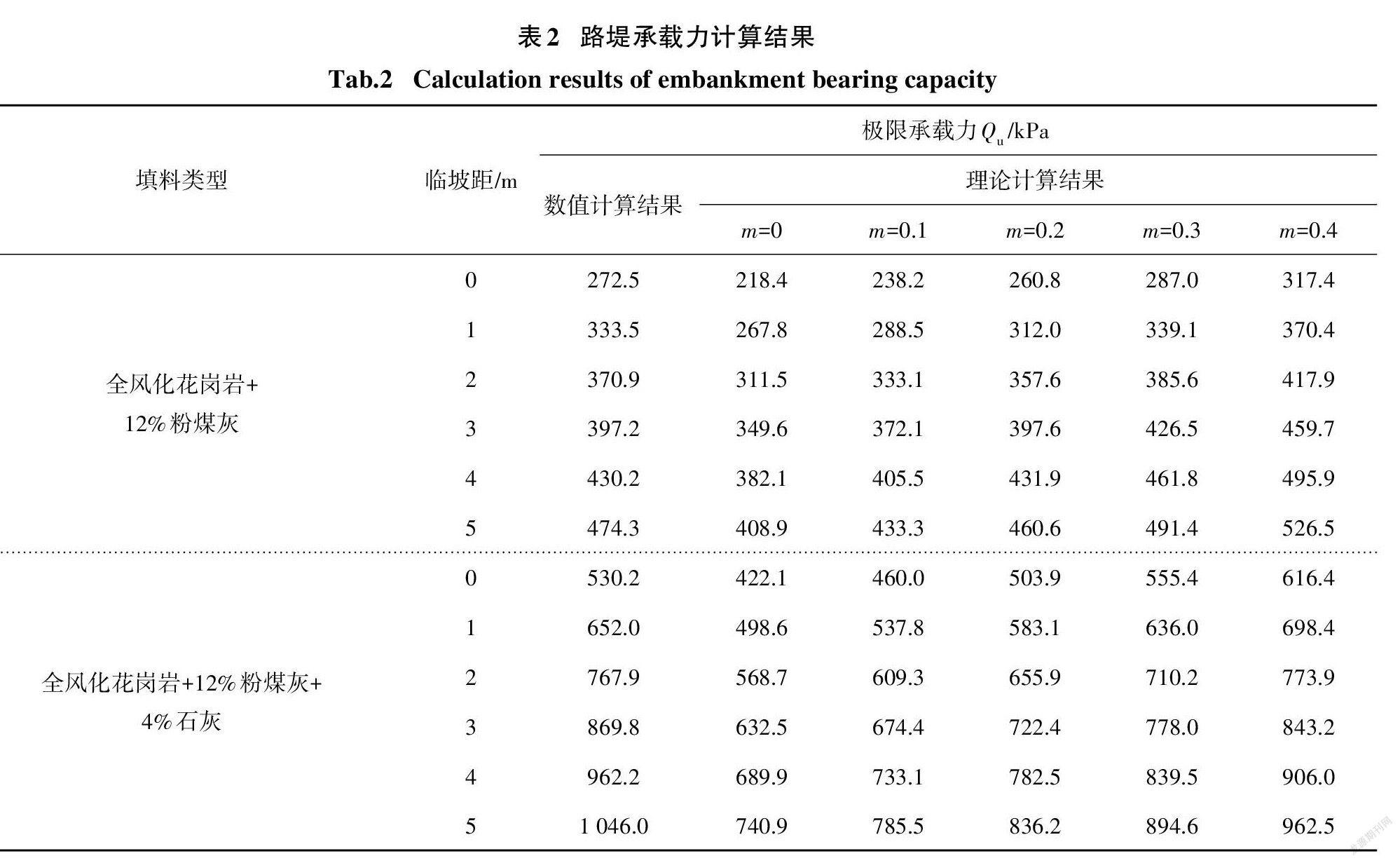
湖南省某高速公路路段为双向四车道，路面宽度为15m，边坡坡率为1：1.5.路面车辆荷载分布根据《公路路基设计规范》（JTGD30—2015）[21]，取为2m.在现场施工时，拟采用两种改性花岗岩作为路堤填料，其黏聚力和内摩擦角如表1所示.将根据本文理论方法获得的不同临坡距下地基承载力计算结果与有限元极限分析软件的数值结果进行对比，如表2所示.

由表2可知，地基承载力随着黏聚力和內摩擦角、临坡距及发挥系数m的增加而增加.当m=0时，双侧破坏模式退化为单侧破坏模式，在不同工况下均会低估极限承载力.大多数工况下，m=0.3时，理论计算结果更接近数值计算结果.综上可知，采用本文理论计算方法预测临坡地基承载力是可行的，尤其是在工程初步设计阶段，选择合适的强度发挥系数即可较为快速准确地判断极限承载力的大小.

5结论

考虑临坡地基各滑块几何尺寸和形状的非对称性，建立了临坡地基双侧破坏的简化分析模型，通过引入土体强度发挥系数考虑远离坡面一侧的土体强度发挥程度，提出了临坡地基承载力的简化分析方法，得出如下结论：

1）边坡的存在导致临坡地基的破坏模式与平地地基存在一定的差异，在设计计算时通常采用单侧破坏模式或双侧破坏模式进行分析.其中，双侧破坏模式可以有效体现路基荷载两侧滑块几何形状及大小非对称的双重特性，二者满足某种条件时，将退化为平地地基破坏模式.

2）基于临坡地基双侧破坏模式，结合极限分析上限定理，提出了可考虑地基破坏模式双侧性的临坡地基承载力简化分析方法.

3）通过工程实例的参数及相应的数值计算结果，验证了本文理论模型及计算方法的可行性.

4）引入强度发挥系数表征远离坡面一侧地基土的强度发挥程度，将多参量优化问题转化为简单的强度发挥系数选取问题并给出了建议取值，便于工程设计人员的应用和初步设计.

参考文献

[1]陈祖煜.土力学经典问题的极限分析上、下限解[J].岩土工程学报，2002，24（1）：1-11.

CHEN Z Y. Limit analysis for the classic problems of soil mechanics [J]. Chinese Journal of Geotechnical Engineering，2002，24 （1）：1-11. （In Chinese ）

[2]王红雨，杨敏.基坑附近既有建筑物地基承载力减损的估算[J]. 土木工程学报，2005，38（8）：95-101.

WANG H Y，YANG M. An estimate for the loss of bearing capacity of the footing near excavations [J]. China Civil Engineering Journal，2005，38（8）：95-101.（In Chinese）

[3]MEYERHOF G G. Some recent research on the bearing capacity of foundations [J]. Canadian Geotechnical Journal，1963，1（1）：16-26.

[4]杨峰，阳军生，张学民，等.斜坡地基单侧滑移破坏模式及承载力上限解[J].工程力学，2010，27（6）：162-168.

YANG F，YANG J S，ZHANG X M，et al. One-side slip failure mechanism and upper bound solution for bearing capacity of foundation onslope[J]. Engineering Mechanics，2010，27（6）：162-168.（In Chinese）

[5]胡卫东，曹文贵.基于非对称破坏模式的临坡地基承载力上限极限分析方法[J].中国公路学报，2014，27（6）：1-9.

HU W D，CAO W G. Upper limit analysis method for ultimate bearing capacity of ground foundation adjacent to slope based on asymmetry failure mode [J]. China Journal of Highway and Transport，2014，27（6）：1-9. （In Chinese）

[6]马庆宏，朱大勇，雷先顺，等.无黏性土斜坡地基承载力模型试验研究[J].岩土工程学报，2014，36（7）：1271-1280.

MA Q H，ZHU D Y，LEI X S，et al. Model tests on bearing capacity of footing on sand slopes[J]Chinese Journal of Geotechnical Engineering，2014，36（7）：1271-1280 （In Chinese）

[7]TURKER E，SADOGLU E，CURE E，et al. Bearing capacity of eccentrically loaded strip footings close to geotextile-reinforced sand slope [J]. Canadian Geotechnical Journal，2014，51（8）：884-895.

[8]HUANG C C. Effects of restraining conditions on the bearing capacity of footings near slopes[J]. Soils and Foundations，2019，59 （1）：1-12.

[9]GEORGIADIS K Undrained bearing capacity of strip footings on slopes [J]. Journal of Geotechnical and GeoenvironmentalEngi- neering，2010，136（5）：677-685

[10]GEORGIADIS K. The influence of load inclination on the undrained bearing capacity of strip footings on slopes[J]. Computers and Geotechnics，2010，37（3）：311-322.

[11]LESHCHINSKY B Bearing capacity of footings placed adjacent to c′-φ′slopes [J]. Journal of Geotechnical and Geoenvironmen- tal Engineering，2015，141（6）：04015022

[12]赵明华，胡啸，张锐.临坡地基承载力极限分析上限有限元数值模拟[J].岩土力学，2016，37（4）：1137-1143.

ZHAO M H，HU X，ZHANG R Numerical simulation of the bearing capacity of a foundation near slope using the upper bound finite element method[J]. Rock and Soil Mechanics，2016，37（4）：1137-1143 （In Chinese）

[13]郑刚，于晓旋，杜娟，等.临近边坡的条形基础地基极限承载力数值分析[J].岩土力学，2018，39（10）：3812-3820.

ZHENG G，YU X X，DU J，et al Numerical analysis of ultimate bearing capacity of strip footings near slopes[J]. Rock and Soil Mechanics，2018，39（10）：3812-3820 （In Chinese）

[14]赵明华，许佳准，张锐，等.不排水条件下的临坡条形基础承载力有限元极限分析[J].长安大学学报（自然科学版），2019，39（3）：45-52

ZHAO M H，XU J Z，ZHANG R，et al Bearing capacity of strip footings on undrained slopes using finite element limit analysis [J]. Journal of Chang'an University （Natural Science Edition），2019，39（3）：45-52 （In Chinese）

[15]LI C C，ZHOU A Z，JIANG P M. Eccentric bearing capacity of embedded strip footings placed on slopes[J]. Computers and Geo- technics，2020，119（3）：103352.

[16]尉學勇，王晓谋，怀超.斜坡地基极限承载力上限解计算与分析[J].岩土工程学报，2010，32（3）：381-387.

YU X Y，WANG X M，HUAI C Calculation and analysis of upper limit solution of ultimate bearing capacity of sloping ground [J]. Chinese Journal of Geotechnical Engineering，2010，32（3）：381-387 （In Chinese）

[17]胡卫东，曹文贵.基于双侧非对称破坏模式的临坡地基承载力极限平衡分析方法[J].土木工程学报，2015，48（1）：120-128.

HU W D，CAO W G. The limit equilibrium method for ultimate bearing capacity of ground foundation adjacent to slope based on bilateral asymmetry failure mode[J]. China Civil Engineering Journal，2015，48（1）：120-128 （In Chinese）

[18]胡卫东，曹文贵，袁青松.基于非对称双侧破坏模式的临坡地基承载力上限分析[J].岩土力学，2016，37（10）：2787-2794.

HU W D，CAO W G，YUAN Q S An upper-bound limit analysis of ultimate bearing capacity of ground foundation adjacent to slope based on asymmetric and bilateral failure mode[J]. Rock and Soil Mechanics，2016，37（10）：2787-2794.（In Chinese）

[19]胡卫东，曹文贵.基于滑移线场理论的临坡地基承载力简化分析方法[J].湖南大学学报（自然科学版），2017，44（7）：162-169

HU W D，CAO W G Simplified analysis method of ultimate bearing capacity for footings near slope based on slip line theory[J]. Journal of Hunan University（Natural Sciences），2017，44（7）：162-169 （In Chinese）

[20]蒋洋，王晓谋，郭建坤，等.基于滑移线场理论斜坡条基极限承载力解析解[J].地下空间与工程学报，2018，14（1）：92-100.

JIANG Y，WANG X M，GUO J K，et al Analytical solutions of ultimate bearing capacity for strip foundations on slopes based on slip line theories[J]. Chinese Journal of Underground Space and Engineering，2018，14（1）：92-100 （In Chinese）

[21]公路路基设计规范：JTGD30—2015[S].北京：人民交通出版社，2015.

Specifications for design of highway subgrades：JTG D30—2015 [S]. Beijing：China Communications Press，2015.（In Chinese）