基于并行SPH方法的地震滑坡对桥桩的冲击作用
2022-11-14王占彬张卫杰张健代登辉高玉峰
王占彬 张卫杰 张健 代登辉 高玉峰
摘要:邻近边坡的桥桩结构对滑坡失稳冲击荷载的承受力决定着它能否安全运行,因此对地震荷载下边坡失稳冲击桥桩结构的研究为桥梁工程设计和建设所迫切需要.利用光滑粒子流体动力学方法跟踪粒子特性时间变化和模拟大变形的特性,提出了地震作用边坡滑坡冲击桥桩结构的光滑粒子流体动力学算法,进行了地震加速度幅值、频谱、持时等参数对地震滑坡规律及滑坡冲击桥桩结构影响的研究,并研究了不同线程数对并行计算效率的影響.结果表明,地震加速度幅值增大会加快土体滑动速度和增大冲击体积量,对土体滑动冲击体积量的增大存在地震加速度临界值,大于该临界值时,冲击量增大幅度变大;在一定频率范围内,土体滑动速度和冲击体积量随地震反应谱峰值频率增大而增大,滑动土体对桥桩结构的冲击随之提前;地震持时增长,滑坡体的中部和后缘部分位移明显增大,冲击体积量增大;采用优化算法能够充分利用线程,大幅提高计算效率.
关键词:桥桩结构;滑坡;冲击;地震;光滑粒子流体动力学;并行优化
中图分类号:TU442文献标志码:A
Impact of Earthquake-induced Landslide on Bridge Pile Based on Parallelized SPH Method
WANG Zhanbin1,2,ZHANG Weijie1,ZHANG Jian2,DAI Denghui1,GAO Yufeng1
(1. Key Laboratory of Ministry ofEducation for Geomechanics and Embankment Engineering(Hohai University),Nanjing210098,China;2. College of Architecture and Engineering,Nanjing Vocational Institute of Transport Technology7,Nanjing 211188,China)
Abstract:Whether the bridge pile structures adjacent to the slopes can support the threats of the landslides impact determines that the bridge can provide safe service. Therefore,the research on the slope instability mechanism and the law of sliding mass impact on bridge pile structure under earthquake and rainfall is an urgent need for bridge engineering design and construction. Based on the advantages of Smoothed Particle Hydrodynamics method,such as tracking the time change of particle characteristics and simulating large deformation,a parallelized Smoothed Particle Hydrodynamics algorithm was proposed to simulate the process of earthquake-induced landslides impact on bridge pile structure. The effects of seismic acceleration amplitude,frequency spectrum,duration on analyzing law of impact by rainfall-induced landslide and earthquake-induced landslide on bridge pile structure were analyzed,and the effect of different number of threads on the efficiency of parallel computing were studied. The results showed that the increase of seismic acceleration amplitude can accelerate the soil sliding impact on bridge pile structure and increase the impact volume. There was a seismic acceleration critical value for the increase of soil sliding impact volume. If it was greater than the critical value,the increase of soil sliding volume was larger. In a certain frequency range,the sliding velocity and impact volume of soil increased with the increase of the peak frequency of seismic response spectrum,and the impact of sliding soil on bridge pile structure was accelerated. With the increasing proportion of the earthquake duration,the displacement of the middle and rear edge of the slope increased obviously,and the impact volume of the sliding soil on the bridge pile structure also increased. The optimization algorithm can make full use of threads and greatly improve the computing efficiency.
Key words:bridge pile structure;landslide;impact;earthquake;Smoothed Particle Hydrodynamics;parallel optimization
伴随着我国经济的高速发展,公路和铁路等基础设施的建设和运营需要更安全的自然环境.据交通运输部统计,截至2019年,我国公路桥梁总里程达60 634.6 km,铁路桥梁总里程数超过1 100 km.为振兴和发展西部地区经济,我国积极推进西部大开发和丝绸之路经济带战略,两大战略分别涉及山地面积455万km2和429万km2(按各省份山地面积比例计算得出).桥梁是沟通山区城市的最主要方式之一.桥梁建设和正常运营对边坡稳定环境的要求不断提高.
我国处于环太平洋地震带和欧亚地震带之间,地震频发.截至2019年,我国发生有5人以上死亡或因灾损失达到当地GDP 0.1%以上的地震灾害近30年平均每年4次,累计影响人次达0.75亿,直接经济损失达1 060亿美元.地震导致了大量滑坡事件,桥桩结构因滑坡冲击发生破坏的现象屡屡出现,如1976年唐山7.8级地震中横跨蓟运河的汉沽铁路桥因河岸滑移严重导致桥墩倾斜;2008年汶川地震滑坡导致10座桥梁破坏严重或损毁,如都汶公路新房子大桥、一碗水中桥、顺河大桥等受滑坡冲击出现倾斜、剪断、倒塌等不同程度损坏[1],213国道百花大桥软弱场地土层向河心滑移导致桥桩基础变位、倾斜[2].桥桩结构对滑坡体冲击荷载的承受力大小决定着它能否安全运行,因此研究地震荷载下边坡滑坡冲击桥桩结构过程具有重要意义.
目前,学者们对地震等诱发滑坡对桥桩等结构形成的冲击主要以模型试验、理论解析、数值分析为手段进行研究.在模型试验方面,王友彪等[3]通过调整滑动体中黏土、砂土、砾土和水的质量分数研究土水混合体密度、滑动形态对桥墩承受冲击荷载的影响.在理论解析方面,有学者假设冲击荷载与作用在结构物上静压力成正比[4],但因在理论上冲击荷载是动力问题而非静力问题,该假设未能得到后续较深入的研究.同时也有学者[5]认为该冲击荷载在数值大小上与结构物承受的静压力和滑坡体滑动速度的平方成正比.在数值分析方面,基于网格离散的数值方法如有限单元法、有限差分法等在处理流滑大变形问题时将遭遇困难,故越来越多的学者开始采用无网格分析方法对土体的大变形动力学特性进行研究,其中一些研究(如Huang等[6]、Dai等[7]、Hu等[8]、王斌等[9])利用具有無网格近似、追踪粒子信息和能够较好模拟不同材料相互作用性质的光滑粒子流体动力学(Smoothed Particle Hydrodynamics,简写为SPH)方法与流变模型结合,对地震诱发滑坡的大变形流滑过程进行了数值模拟.Bui等[10]在对岩土体材料滑坡大变形、Chen等[11]在对岩土颗粒材料滑坡大变形的SPH研究过程中,岩土体材料的应力应变关系采用非关联流动法则Drucker-Prager模型进行描述.Huang等[12]在对滑坡中液化土体的大变形土体流滑数值模拟研究中采用土-水耦合SPH方法,土和水分别在不同的计算层,土体采用弹性模型,水体被视为近似不可压缩流体.唐宇峰等[13]采用SPH方法对土体滑动大变形规律进行研究,土体应力应变关系采用Drucker-Prager模型进行描述.Dai等[14]引入流体-结构相互作用SPH模型计算研究了文家沟和洪春沟滑坡对节制坝的冲击影响,滑动土体采用Bingham流体模型.综合分析,学者们基于SPH方法对流态性滑坡的大变形运动特性研究在一定程度上揭示了滑坡的大变形成灾机制,但是这些研究缺少地震滑坡冲击桥桩结构全过程的演化机理分析.
对此,本文基于SPH基本原理提出用于模拟分析地震滑坡冲击桥桩结构灾变过程的并行SPH计算方法,形成自编程序,采用Arias烈度增加值方法截取地震波以减少计算空间的浪费,基于该方法研究不同地震加速度幅值、频谱和持时条件下滑坡对桥桩结构的冲击规律,并研究不同线程数对并行计算效率的影响.
1并行SPH地震滑坡冲击模型的建立
1.1SPH滑坡冲击的基本原理
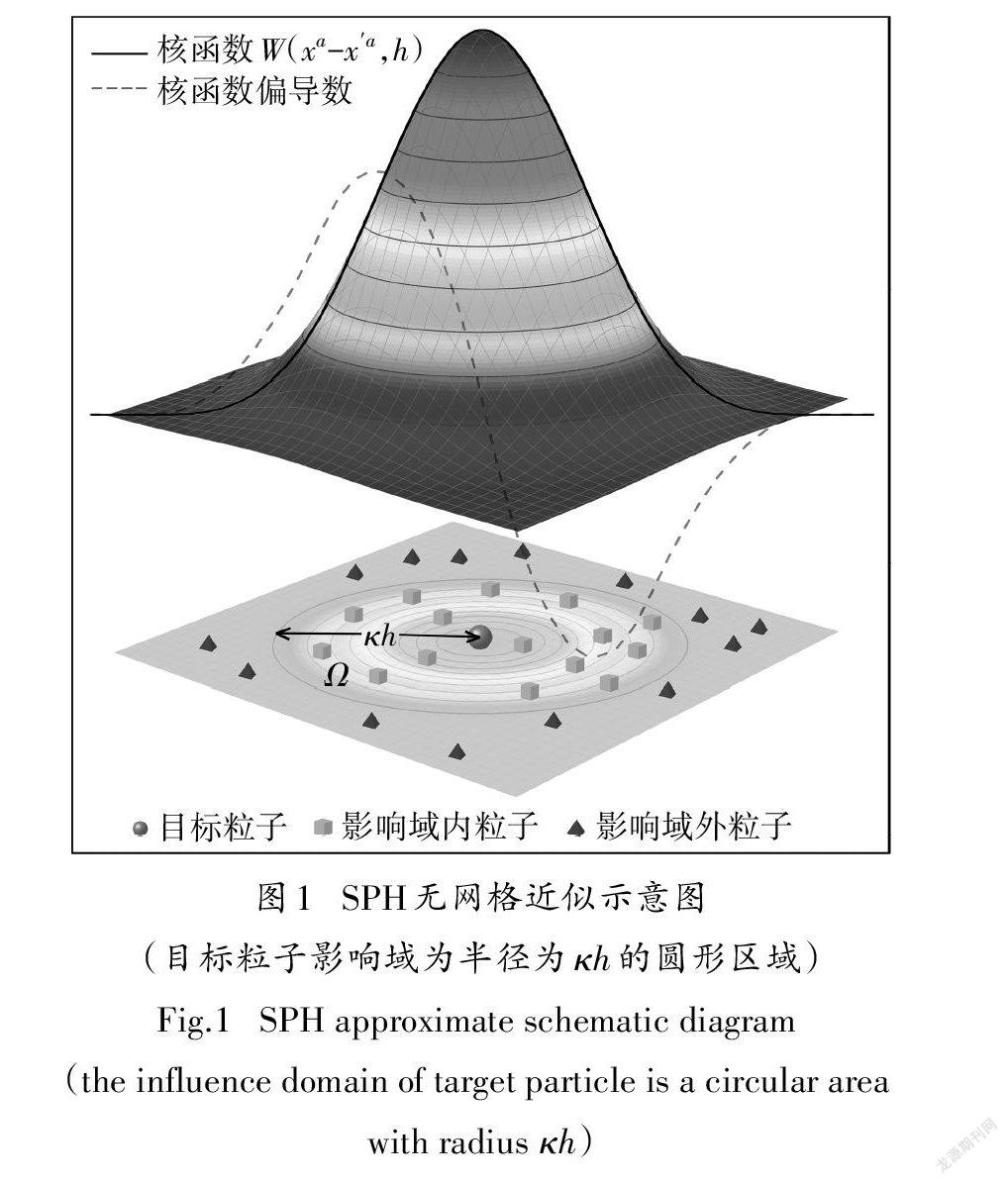
SPH方法是一种拉格朗日无网格近似方法,将计算区域划分为一定数目的粒子,每个粒子都包含着自有的场变量,如速度、应力、压力、质量、密度等. 实体运动、变形等所有信息由这些粒子承载,同时追踪每个粒子的运动,无网格及粒子间相互作用的特点使其更易处理大变形问题.SPH无网格近似过程(如图1所示)包括核近似和粒子近似,假设场函数为f(x),则它的核近似和粒子近似表达式分别如式(1)(2)所示:
式中:上标α表示坐标方向;特征宽度参数h是定义光滑核函数影响区域的光滑长度;W是光滑核函数;N是粒子i影响域内的粒子数量;mj、ρj分别是粒子j的质量、密度;Wij是粒子i在粒子j位置的值.
SPH方法的基本控制方程包括连续方程、动量方程和能量方程[15].本研究中将地震滑坡冲击桥桩结构的过程假设为等温过程,因此不考虑能量方程,得到无网格近似后的连续方程、动量方程表达式如式(3)(4)所示:
为了提高SPH计算方法在边界上的精度,将控制方程表达式用影响域内粒子核函数和的形式进行归一化[16-18],得到:
1.2SPH滑坡冲击的土-结构模型
研究中结构粒子的控制方程采用的应力形式为Piola-Kirchhoff第一应力张量,质量守恒和动量守恒以完全Lagrange方法表示,采用的归一化表达式如式(7)(8)所示:
ρiJi=ρ0(7)
由滑动土体对结构体的冲击动量方程得到:
通过影响域内为土体粒子的无网格粒子近似得到如下形式表达式:
1.3SPH滑坡冲击的并行优化
Amdahl定律给出了算法在运用并行计算之后,运行加速的估算[20].假设算法按串行计算消耗的时间为小按并行计算消耗的时间为tp,tp分为并行计算部分和非并行计算部分,其中非并行计算部分的时间为ts,则可得到
式中:N是并行处理器的数量.得到加速比sp:
式中:假设并行处理器数N趋近无穷大时,加速比为sp=t1/ts.这反映了并行程序的加速比主要受限于非并行计算部分的时间t s,也显示出了算法的运行中并行计算的部分占比越多,所消耗的时间越少.本研究采用张卫杰等[21]提出的并行计算方法.
1.4SPH滑坡冲击的地震加速度施加和验证
本研究中土体采用的Drucker-Prager模型是Bui等[10]改进的弹性-完全塑性土体本构模型.地震边坡滑坡研究中土体阻尼系数和弱化指数借鉴Chen[22]对地震边坡滑坡的研究.验证模型中采用下负荷屈服面剑桥模型[23],参数如表1所示.计算模型两侧边界设置为吸能边界,以此防止地震波传播到边界时,边界再反射回来对试验模型或计算模型造成影响(如图2所示,左侧为刚体边界,右侧为吸能边界),以模拟实际场地的半无限区域特性,地震波由底部输入,振动方向为水平.
为验证所提出方法在地震作用下土体大变形滑坡方面的应用,建立边坡振动SPH模型如图3所示. 输入的地震波采用修正Kobe波,地震加速度为水平向.计算模型滑动土体部分由砂土粒子和软黏土粒子间隔等间距分布、硬土层由砂土粒子和硬黏土粒子间隔等间距分布,软黏土和砂土混合而成的边坡土体厚度为20.1 cm,坡度为27.9°,硬黏土和砂土混合而成的边坡土体左侧厚4.8 cm、右侧厚28 cm.模型箱宽1.6 m,高0.384 m.初始粒子间距0.8 cm,软黏土粒子数为1 267,硬黏土粒子数为1211,砂土粒子数为2 479,水体粒子数为4 957,地震边界粒子数为897.左右两侧各设置3层吸能边界粒子,其数值为270.砂土密度为2 130kg/m3,采用Drucker-Prager模型,剪切波速79.5 m/s,泊松比0.3,内摩擦角30°,渗透系数1×10-4m/s,軟黏土和硬黏土采用能够描述软化和硬化行为的下负荷面剑桥模型,材料参数如表1 所示,混合土体密度均为1 760kg/m3,混合土体为饱和状态,计算结果与振动台试验数据(Wartman等[24])进行对比.
图4和图5分别给出了振动后土体粒子分布图和振动后土体粒子最大剪应变云图.从图4中可以看出,计算结果振后软黏土粒子外轮廓线与物理模型试验振后土体轮廓线较接近,表明计算模型的振后土体滑动位移与物理模型的土体滑动位移大致相近.试验土体变形较计算值大,原因是试验中软化土层的下部和硬化土层的上部分别被嵌附一层0.5 mm 厚光滑的高密度聚乙烯土工膜作为预设滑动面,从云图中可以看出,土体最大剪应变位置沿软化土层和硬化土层接触面出现,由此可得出结论:计算值和试验值的土坡滑动规律大致相同.
1.5SPH滑坡冲击桥桩结构的数值模拟工况
Arias烈度(Ia)[25]是反映观测点地震加速度产生能量大小的重要指标,Ia综合考虑了地震动幅值、地震动频率和地震动持续时间的影响,已被很多学者[26-28]用于地震边坡滑坡潜在危险分析.0.8g峰值加速度的Kobe地震波加速度持续时间为42 s,时程曲线如图6所示,其Arias烈度达0.583 m/s,在5.29~20.29 s时段内Arias烈度增长幅度为0.575 m/s,占总增长的99.02%,说明该地震在此测点15 s时间段内能够释放大部分的能量.选取5.98~20.98 s时段Kobe地震波和全时程地震波作为计算模型的地震动输入.后文将42 s Kobe地震波和5.29~20.29 s时段Kobe地震波分别简称为Kobe波和Kobe截取波.
本研究计算采用的地震峰值加速度为0.2g、0.4g、0.6g、0.8g;地震反应谱以时间变化系数的形式进行改变:0.5、1.0、2.0;地震持续时间选取1次和叠加2次相同的典型时段截取波.
2地震滑坡对桥桩结构的冲击规律
2.1原波与截取波荷载下滑坡结果对比
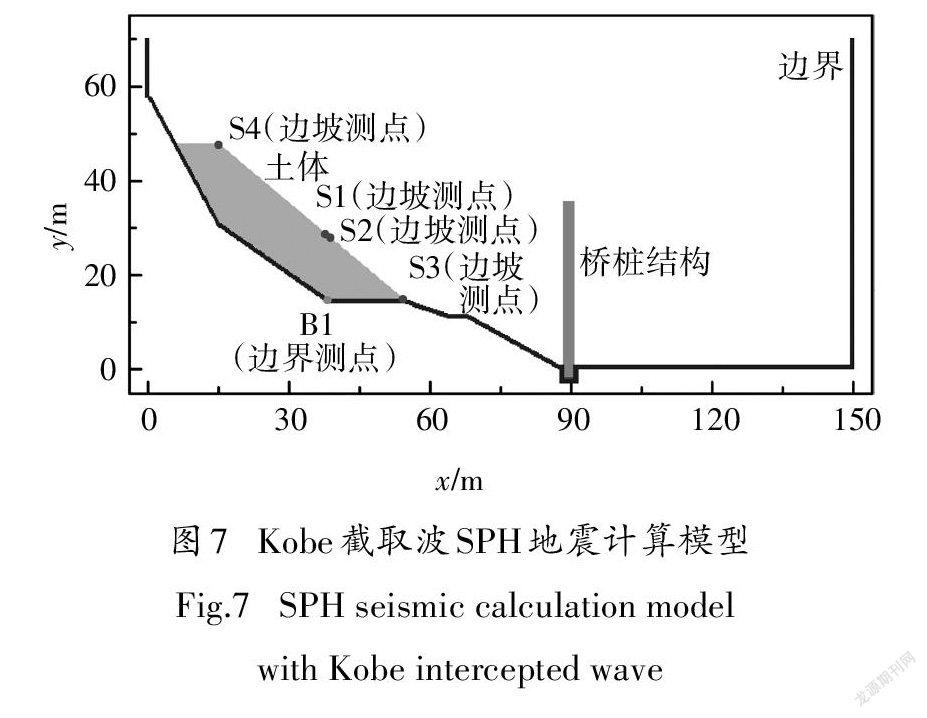
为比较Kobe截取波和Kobe波在本研究算例的差别,选取5.98~20.98 s时段Kobe地震波和全时程地震波作为计算模型的地震动输入,建立模型如图7 所示.布置4个边坡测点和1个边界测点,编号分别为S1、S2、S3、S4、B1,其中S1、S2分别是42 s Kobe地震波和15 s Kobe截取地震波计算模型总位移最大值点,S3、S4分别是边坡坡脚和坡顶的测点,B1用于测量边界在施加42 s Kobe地震波和15 s Kobe截取地震波加速度之后得到该点的位移,验证地震加速度施加情况.
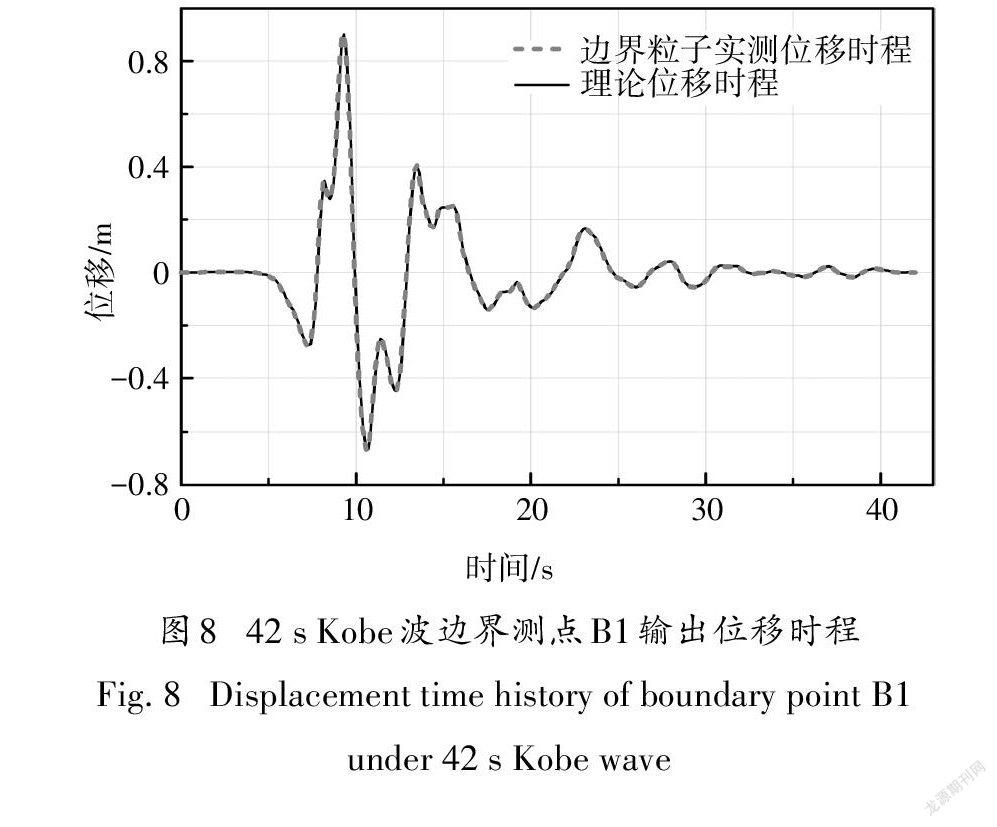
如图7所示,所建模型采用的粒子间距为0.25 m,粒子总数为13 623,其中滑动土体粒子数为8 592,桥桩结构粒子数为1 350,边界粒子数为3 681.土体采用DP模型,参数见表2.边界测点B1施加两种地震波后的计算结果如图8、图9所示,从图中可看出SPH测得位移时程与实际加速度积分后得到的理论值基本一致,随着时间的推移,理论位移偏移终值分别为0.05 mm、-20.56 mm,SPH计算值分别为1.23 mm、-41.15 mm,位移累积偏移差值分别为1.18mm、-20.59mm.
图10~图13分别给出了4个测点S1、S2、S3、S4 在42 s Kobe波和15 s Kobe截取波作用下的水平向和竖向位移对比.从图中可以看出S1测点15 s地震波输入工况相较于42 s地震波输入工况在水平向和竖向存在最大3.4 s的延迟位移,42 s地震波输入工况最大水平位移为40.60m、竖向位移为-15.29 m,15 s地震波输入工况最大水平位移为40.42m、竖向位移为-14.58 m,水平向和竖向最大位移差分别为0.18m、0.71 m,差值占比分别为0.44%、4.65%;S2测点15 s地震波输入工况相较于42 s地震波输入工况在水平向和竖向存在最大3.4 s的延迟位移,42 s地震波输入工况最大水平位移为40.54m、竖向位移为-15.36 m,15s地震波输入工况最大水平位移为40.53m、竖向位移为-14.72 m,水平向和竖向最大位移差分别为0.01m、0.64m,差值占比分别为0.02%、4.14%;S3测点15 s地震波输入工况相较于42 s地震波输入工况在水平向和竖向存在最大3.3 s的延迟位移,42 s地震波输入工况最大水平位移为34.30 m、竖向位移为-13.76 m,15 s地震波输入工况最大水平位移为34.10m、竖向位移为-13.97 m,水平向和竖向最大位移差分别为0.20 m、0.21 m,差值占比分别为0.58%、1.53%;S4测点15 s地震波输入工况相较于42 s地震波输入工况在水平向和竖向存在最大3.5 s 的延迟位移,42 s地震波输入工况最大水平位移为24.84m、竖向位移为-19.81 m,15s地震波输入工况最大水平位移为23.57m、竖向位移为-19.73 m,水平向和竖向最大位移差分别为1.27 m、0.08 m,差值占比分别为5.12%、0.40%.
图14、图15分別给出了两种地震波作用下的总位移云图.从图中可以看出滑动土体粒子的位移规律是相似的,即滑动机理没有因为截取地震波输入而出现与原波差距较大的变化.由两者的计算结果比较可知桥桩结构所受荷载、滑动土体位移在两种地震动输入情况下相差很小,为提高研究效率,选取此15 s时段地震加速度作为本小节数值模型计算研究的地震输入.
2.2地震加速度幅值的影响
建立计算模型如图16所示.布置测点S1,坐标(52.75,16.25),用于监测位移变化;布置A-A断面,横坐标为54.25,用于监测滑坡土体通过此断面的体积量.所研究地震加速度幅值分别为0.2g、0.4g、0.6g,0.8g. 土体参数如表2所示.
图17~图20分别给出了0.2g、0.4g、0.6g、0.8g峰值加速度作用下的位移云图.从图17、图18中可以看出,0.2g峰值加速度和0.4g峰值加速度作用下土体最终位移和滑动的土体体积量很接近(0.2 g工况S1测点最大水平向位移为34.71 m,最大竖向位移为-13.89 m;0.4g工况S1测点最大水平向位移为34.76 m,最大竖向位移为-13.83 m),4种峰值加速度作用下的S1测点最终位移均很接近的原因是该测点与桥桩结构的水平距离为35.28 m,0.6g工况S1测点最大水平向位移为34.71m,0.8g工况S1测点最大水平向位移为35.46 m,与该测点和桥桩结构水平距离相差很小,该测点经过地震荷载作用已滑动到接近桥桩结构的位置.
图21给出了4种峰值加速度作用下S1测点水平向和竖向位移-时间关系对比曲线,从图中可以看出,0.4g峰值加速度作用下土体位移快速增大的时间要早于0.2 g峰值加速度作用下的土体位移快速增大的时间4.2 s. 0.6g峰值加速度作用下土体位移快速增大的时间要早于0.2 g峰值加速度作用下的土体位移快速增大的时间7.6 s. 0.8g峰值加速度作用下土体位移快速增大的时间要早于0.2 g峰值加速度作用下的土体位移快速增大的时间9.5 s.这说明峰值加速度的提高加速了边坡的破坏和加大了边坡的滑坡体积量.监测断面A-A,0.2 g通过此断面体积量为51.81 m3,占比9.65%;0.4g 为54.94 m3,占比10.23%;0.6g 为90.19 m3,占比16.79%;0.8g 为266.125 m3,占比49.56%.监测断面数据也说明0.2g峰值加速度工况和0.4g峰值加速度工况滑坡体积量很相近,0.6g峰值加速度工况滑坡体积量稍大于0.2 g和0.4 g工况滑坡体积量,0.8 g峰值加速度工况滑坡体积量最大,且超过0.2g工况滑坡5倍之多.地震加速度幅值的提高在增加土体边坡滑坡体积量的同时,也加快了边坡土体的滑动破坏.
2.3地震加速度频谱的影响
为研究不同地震加速度频谱对边坡滑坡冲击桥桩荷载的影响,将15 s Kobe截取地震波压缩至7.5 s和延长至30s,定义时间变化系数为现研究地震波时长与原时长的比值.本节所选取的时间变化系数tvc为0.5、1.0、2.0.3种时间变化系数的地震加速度时程如图22所示.它们经过傅里叶变换以频域的形式展示如图23所示,它们的波峰频率分别为0.27、0.54、1.08,随着时间变化系数的提高,波峰频率增大.计算模型如图16所示,布置测点S1,坐标(52.75,16.25),用于监测位移变化;布置4T断面,横坐标为54.25,用于监测滑坡土体通过此断面的体积量.土体参数如表2所示.
图24、图25分别给出了时间变化系数为0.5和2.0的边坡地震位移云图,图26给出了3种时间变化系数下地震边坡模型S1测点水平向位移、竖向位移与时间的对比关系曲线.从位移云图中可以看出,时间变化系数为0.5时最大位移和最小位移分别为37.4 6m、2.05 m,通过断面A-A的体积量为59.31 m3,占滑坡体总体积量的11.05%;时间变化系数为1.0时最大位移和最小位移分别为43.13 m、20.53 m,通过断面A-A的体积量为266.13 m3,占滑坡体总体积量的49.56%;时间变化系数为2.0时最大位移和最小位移分别为43.65 m、17.71 m,通过断面A-A的体积量为273.44 m3,占滑坡体总体积量的46.08%.时间变化系数由0.5增大至1.0,土体滑坡位移和体积量会明显增多,时间变化系数由1.0增大到2.0,土体滑坡最终位移和滑动体积量无明显变化.图26中时间变化系数2.0相较于1.0时在15~30 s出现的水平位移波动由边界位移波动引起,边界位移波动如图9所示.从中也可以看出,时间变化系数由1.0减小至0.5,延缓了滑坡体的位移变化(延缓约2.6 s),也减小了滑坡体的滑动速度,时间变化系数由1.0增大至2.0,滑坡位移未出现较大变化,提前约0.9 s,较小程度地提高滑坡体的滑动速度,原因可能是边坡土体在时间变化系数为1.0的情况下已经达到足够大的滑坡位移.
2.4地震加速度持时的影响
建立计算模型如图27所示,布置测点S1、S2,坐标分别为(52.75,16.25)和(38.75,28),用于监测位移变化;布置A-A断面,横坐标为54.25,用于监测滑坡土体通过此断面的体积量.所考虑的地震加速度持时影响是选取1次的15 s Kobe截取波和2次截取波时间上的叠加,持续时间分别为15 s、30 s.土体参数如表2所示.
图20、图28分别给出了1次15 s Kobe截取地震波和2次叠加截取地震波的位移云图,图29、图30给出了两种持续时间下地震边坡模型S1、S2测点水平向位移、竖向位移与时间的关系对比曲线.从云图中可以看出,2次叠加截取地震波最终最大和最小位移分别为45.59 m、21.26m,高于1次截取地震波边坡最大位移和最小位移2.46 m,0.73 m,1次截取地震波边坡最大和最小位移分别为43.13 m,20.53 m. 1次截取地震波和2次叠加截取地震波滑坡土体通过断面A-A的体积量相同,均为266.125 m3,占滑坡体总体积量的49.56%,滑坡体积量均很大.从位移-时间关系曲线中可以看出,2次叠加截取地震波与1次截取地震波作用的边坡,对S1测点位移的影响差别很小,但对S2测点在15 s(即第1次截取地震波作用结束后)出现增大,S2测点最终水平位移、竖向位移在1次和2次叠加截取地震波作用下分别为40.53 m、14.72 m和43.03 m、15.06 m,2次多于1次2.5 m、0.34 m.這说明2次叠加截取地震波对滑坡体的中部和后缘部分位移影响较大,对前缘部分无较大影响.
2.5SPH滑坡冲击模型的并行优化效率
为验证并行优化的效率,计算研究了线程数分别为1、2、4、6、8、10、12、16、20、24、28,峰值加速度分别为0.2g、0.4g、0.6g、0.8g,时间变化系数Rt分别为0.5、1.0、2.0,施加1次截取波、循环施加2次截取波地震作用下边坡土体滑动冲击桥桩结构工况(其中峰值加速度为0.8 g,时间变化系数Rt为1.0,1次15 s截取Kobe波为同一工况,在图中简写为0.8g),按式(13)得到各线程数下的加速比sp(多线程和单线程计算消耗时间的比值),如图31所示.图中虚线为加速比随线程数增加的均值趋势线,从图31中可以看出,在该计算平台下,线程数从1增加到8,加速比呈快速增长趋势;线程数从8增加到20,加速比增长速度稍缓;线程数从20增加到28,加速度增长很缓慢,表明计算中线程数为20~28时,计算机处理效能的利用已接近或达到最大状态.线程数为28时最大达6.1,平均5.7,其计算时间近似是单线程计算时间的1/6.该结果说明本研究土-结构耦合SPH并行方法极大地提高了地震作用下边坡土体滑移计算效率,减少了计算时间.
3结论
1)基于SPH方法的基本原理,建立了考虑静压力和相对速度产生的压力的土-结构粒子相互作用模型,通过地震滑坡模型验证了SPH方法模拟振动台试验的准确性.
2)根据Arias烈度增长值确定15 s截取Kobe地震波代替42 s原Kobe地震波,减小了对计算空间的浪费.
3)高地震加速度幅值会大幅增加可滑动土体的体积量,0.4g相对于0.2g滑坡体积量增加不明显,0.8 g滑坡体积量超过0.2 g滑坡5倍之多,低地震加速度幅值会大幅加快滑动速度,0.4 g下土体位移快速增大的时间要早于0.2g下的时间4.2 s,0.8g下土体位移快速增大的时间要早于0.6g下的时间1.9 s.
4)地震加速度频率由0.27增大至0.54,土体滑坡体积量增大近4倍,滑动位移加快2.6 s,由0.54增大到1.08,土体滑坡体积量无明显变化,滑动位移加快0.9 s.
5)地震加速度持时对滑坡体后缘部分影响较大,对后缘测点的位移增加明显高于前缘测点,滑动到桥墩结构的累积土体体积量随持时的增加而增加.
6)对多种工况的SPH程序进行不同线程数的并行优化,总结得出线程数从1增加到8,加速比呈快速增长趋势;线程数从8增加到20,加速比增长速度稍缓;线程数从20增加到28,加速度增长很缓慢,表明计算中线程数为20~28时,计算机处理效能的利用已接近或达到最大状态.
参考文献
[1]庄卫林,刘振宇,蒋劲松.汶川大地震公路桥梁震害分析及对策[J].岩石力学与工程学报,2009,28(7):1377-1387.
ZHUANG W L,LIU Z Y,JIANG J S. Earthquake-induced damage analysis of highway bridges in Wenchuan earthquake and countermeasures [J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(7):1377-1387.(In Chinese)
[2]王东升,郭迅,孙治国,等.汶川大地震公路桥梁震害初步调查[J].地震工程与工程振动,2009,29(3):84-94.
WANG D S,GUO X,SUN Z G,et al. Damage to highway bridges during Wenchuan earthquake [J]. Journal of Earthquake Engineering and Engineering Vibration,2009,29 (3):84-94. (In Chinese)
[3]王友彪,姚昌荣,刘赛智,等.泥石流对桥墩冲击力的试验研究[J].岩土力学,2019,40(2):616-623.
WANG Y B,YAO C R,LIU S Z,et al. Experimental study of debris flow impact forces on bridge piers [J]. Rock and Soil Mechanics,2019,40(2):616-623.(In Chinese)
[4]HUNGR O,MORGAN G C,KELLERHALS R. Quantitative analysis of debris torrent hazards for design of remedial measures [J]Canadian Geotechnical Journal,1984,21(4):663-677
[5]ZANUTTIGHB,LAMBERTI A. Experimental analysis of the impact of dry avalanches on structures and implication for debris flows [J]. Journal of Hydraulic Research,2006,44(4):522-534.
[6]HUANG Y,CHENG H L,DAI Z L,et al. SPH-based numerical simulation of catastrophic debris flows after the 2008 Wenchuan earthquake [J]. Bulletin of Engineering Geology and the Environment,2015,74(4):1137-1151.
[7]DAI Z L,HUANG Y,CHENG H L,et al. 3D numerical modeling using smoothed particle hydrodynamics of flow-like landslide propagation triggered by the 2008 Wenchuan earthquake[J]. Engineering Geology,2014,180:21-33.
[8]HU M,LIU M B,XIE M W,et al. Three-dimensional Run-out analysis and prediction of flow-like landslides using smoothed particle hydrodynamics[J].Environmental Earth Sciences,2015,73 (4):1629-1640.
[9]王斌,周傲,陆盟,等.非饱和流固耦合物质点方法(CMPM)的原理及应用[J].湖南大学学报(自然科学版),2022,49(5):192-202.
WANG B,ZHOU A,LU M,et al. Formulations and applications of coupled material point method for unsaturated soils[J]. Journal of Hunan University(Natural Sciences),2022,49(5):192- 202.(In Chinese)
[10]BUI H H,FUKAGAWA R,SAKO K,et al. Lagrangian meshfree particles method(SPH)for large deformation and failure flows of geomaterial using elastic-plastic soil constitutive model[J]. International Journal for Numerical and Analytical Methods in Geo- mechanics,2008,32(12):1537-1570.
[11]CHEN W,QIU T. Numerical simulations for large deformation of granular materials using smoothed particle hydrodynamics method [J]. International Journal of Geomechanics,2012,12(2):127-135.
[12]HUANG Y,ZHANG W J,DAI Z L,et al.Numerical simulation of flow processes in liquefied soils using a soil-water-coupled smoothed particle hydrodynamics method [J]. Natural Hazards,2013,69(1):809-827.
[13]唐宇峰,施富強,廖学燕,等.基于光滑粒子流体动力学的流动法则对土体滑坡大变形的影响探讨[J].岩土力学,2018,39(4):1509-1516.
TANG Y F,SHI F Q,LIAO X Y,et al. Determination on flow rules of large deformation analysis of slope using SPH method[J]. Rock and Soil Mechanics,2018,39(4):1509-1516.(In Chinese)[14]DAI Z L,HUANGY,CHENG H L,et al. SPH model for fluid - structure interaction and its application to debris flow impact estimation[J].Landslides,2017,14(3):917-928.
[15]張卫杰,高玉峰,黄雨,等.水土耦合SPH数值模型的正则化修正及其应用[J].岩土工程学报,2018,40(2):262-269.
ZHANG W J,GAO Y F,HUANG Y,et al.Normalized correction of soil-water-coupled SPH model and its application[J]. Chinese Journal of Geotechnical Engineering,2018,40(2):262-269. (In Chinese)
[16]RANDLES P W,LIBERSKY L D. Smoothed particle hydrodynamics:some recent improvements and applications[J]. Computer Methods in Applied Mechanics and Engineering,1996,139 (1/2/3/4):375-408.
[17]CHEN J K,BERAUN J E,CARNEY T C.A corrective smoothed particle method for boundary value problems in heat conduction [J].International Journal for Numerical Methods in Engineering,1999,46(2):231-252.
[18]CHEN J K,BERAUN J E.A generalized smoothed particle hydrodynamics method for nonlinear dynamic problems[J]. Computer Methods in Applied Mechanics and Engineering,2000,190(1/2):225-239.
[19]ADAMI S,HU X Y,ADAMS N A. A generalized wall boundary condition for smoothed particle hydrodynamics[J]. Journal of Computational Physics,2012,231(21):7057-7075.
[20]AMDAHL G M. Validity of the single processor approach to achieving large scale computing capabilities[C]//Proceedings of the April 18-20,1967,Spring Joint Computer Conference on- AFIPS,67(Spring). New York:ACM Press,1967:483-485.
[21]张卫杰,郑虎,王占彬,等.基于三维并行SPH模型的土体流滑特性研究[J].工程地质学报,2018,26(5):1279-1284.
ZHANG W J,ZHENG H,WANG Z B,et al.Study on flowing behavior of soil based on three dimensional and parallelized SPH model[J]. Journal of Engineering Geology,2018,26(5):1279- 1284.(In Chinese)
[22]CHEN W. Numerical studies of seismically induced slope deformation using smoothed particle hydrodynamics method[D].State College:The Pennsylvania State University,2012.
[23]张锋.计算土力学[M].北京:人民交通出版社,2007:40-51.
ZHANG F. Computational soil mechanics [M]. Beijing:China Communications Press,2007:40-51.(In Chinese)
[24]WARTMAN J,SEED R B,BRAY J D. Shaking table modeling of seismically induced deformations in slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering,2005,131 (5):610-622.
[25]ARIAS A. A measure of earthquake intensity[M]//HANSEN R J. Seismic design for nuclear power plants. Cambridge,MA:MIT Press,1970:438-483.
[26]LEE C T,HSIEH B S,SUNG C H,et al. Regional Arias intensity attenuation relationship for Taiwan considering VS30[J]. Bulletin of the Seismological Society of America,2012,102(1):129-142.
[27]PELAEZ J A,DELGADO J,LOPEZ CASADO C. A preliminary probabilistic seismic hazard assessment in terms of Arias intensity in southeastern Spain[J]. Engineering Geology,2005,77(1/2):139-151.
[28]王秀英,聂高众,张玲,汶川地震触发崩滑与Arias强度关系研究[J].应用基础与工程科学学报,2010,18(4):645-656.
WANG X Y,NIE G Z,ZHANG L. Relationship between landslides induced by the Wenchuan earthquake and Arias intensity [J]. Journal of Basic Science and Engineering,2010,18(4):645- 656.(In Chinese)
