多AUV分布式模型预测深度和纵向速度控制
2022-11-14边有钢张俊杰李崇康徐彪秦兆博胡满江
边有钢 张俊杰 李崇康 徐彪 秦兆博 胡满江







摘要:针对多自主水下航行器(Autonomous Underwater Vehicle,AUV)的深度和纵向速度耦合控制问题,提出一种基于分布式模型预测控制(Distributed Model Predictive Control,DMPC)的双子系统控制方法.在DMPC的框架下,AUV和邻居共享信息以建立预测优化问题,实现多AUV的协同控制.考虑单个AUV的深度和纵向速度控制,深度控制子系统参考轨迹中的俯仰角序列作为速度控制子系统中俯仰角的实际值,同时纵向速度控制子系统参考轨迹中的纵向速度序列作为深度控制子系统中纵向速度的实际值,由此解耦为两个子系统,进而独立地求解预测优化问题.仿真实验结果表明,相对于整体系统DMPC方法,本文提出的双子系统DMPC方法可在牺牲一定深度控制收敛速度的基础上降低计算时间73.3%.
关键词:自主水下航行器;分布式模型预测控制;深度控制;纵向速度控制
中图分类号:U66;O232文献标志码:A
Distributed Model Predictive Depth and Surge Velocity Control of Multiple Autonomous Underwater Vehicles
BIAN Yougang1,2,ZHANG Junjie1,LI Chongkang1,XU Biao1,2,QIN Zhaobo1,2,HU Manjiang1,2
(1. College of Mechanical and Vehicle Engineering,Hunan University,Changsha 410082,China;2. Wuxi Intelligent Control Research Institute,Hunan University,Wuxi 214115,China)
Abstract:A distributed model predictive control (DMPC)based two-subsystem approach is proposed in this paper to resolve the coupled surge velocity and depth control problem of multiple Autonomous Underwater Vehicles (AUVs). For the motion coordination of multiple AUVs,each AUV shares information with its neighbors to solve local predictive optimization problems under the framework of DMPC. For the motion coordination of the surge velocity and depth control subsystems of a single AUV,the predicted surge velocity from the surge velocity control subsystem is approximately lent to the depth control subsystem,of which the predicted pitch angular velocity is sent back to decouple the dynamics and solve the predictive optimization problem. The simulation results show that compared with the coupling model approach,the proposed two-subsystem approach sacrifices some rate of convergence in depth but reduces the calculation time by 73.3%.
Key words:Autonomous Underwarter Vehicles(AUV);Distributed Model Predictive Control (DMPC);depth control;surge velocity control
自主水下航行器(Autonomous Underwater Vehicle,AUV)是一種高度智能的装备,它不依赖驾驶员的操作,并且与母船没有物理连接[1].由于能够携带各种设备在载人航行器无法到达的水域长时间工作,AUV在水下救援[2]、资源勘探[3]、管道探测[4]等方面发挥着重要作用.随着资源勘探和海底检测等商业和军事应用的任务规模和复杂性不断增加,多AUV协同相较于单AUV在经济性和可靠性上的优势越来越大[5-6].因此,协同控制作为可以实现多AUV的协调运动的控制方法,受到研究者的普遍关注.
关于AUV协同控制,现有研究采用了多种控制方法,如基于共识的方法、滑模控制法、反步控制法和人工势场方法等.Yan等[7]设计了一种共识控制策略来解决具有模型不确定性和外部干扰的跟踪共识问题,其中考虑了固定的和切换的通信拓扑.Gao等[8]提出了一种带扰动观测器的滑模控制方法,该方法能在有限时间内实现扰动下的全局稳定.Rout等[9]在Lyapunov方法的基础上开发了一种反步法来实现领航者-跟随者队列控制.Sahu等[10]将模糊人工势函数应用于多AUV的控制,该方法在障碍物环境下优于传统的数学方法.此外,许多研究者采用了自适应控制方法[11-12].
对于AUV的运动控制,Yao等[13]引入了一种改进的模型预测控制(Model Predictive Control,MPC)方法来解决深度控制问题,该方法中权重矩阵随误差变化而变化,但在Yao的研究中没有涉及到纵向速度的控制.在Zhou等[14]的研究中,提出了一种基于优选的最优控制方法,可以根据控制器数据库选择最优控制方式.Khodayari等[15]提出了一种自适应模糊PID控制方法来实现自主水下航行器的深度、纵向速度和航向控制,与传统的PID控制器相比,该方法具有更好的鲁棒性和动态特性.除此之外,强化学习[16]和滑模控制[17]也被用于AUV的运动控制.
在实际的编队中,希望在保持低能耗的同时获得较好的性能,同时系统的约束条件也需要严格满足.然而,上述大多数方法都难以综合处理这些问题.模型预测控制在处理系统约束和非线性动力学方面具有一定的优势[18].继承模型预测控制上述优势的分布式模型预测控制(Distributed Model Predictive Control,DMPC)可以给每一个单体都定义优化问题,并且各单体之间独立地求解优化问题,而不是将全局优化问题的计算集中在一个控制器中.相对于集中式模型预测控制,DMPC可以通過局部信息实现全局协调,也大大提高了控制的实时性[19],在地面车辆领域已经得到了广泛的应用[20-21].AUV的动力学模型具有复杂、非线性特点,模型预测控制由于具有处理约束和非线性系统的优势,因此被广泛应用于水下航行器[22-23].此外,由于可以根据实际需求设计代价函数,DMPC在实际应用中具有较大的灵活性.Li等[22]提出了编队跟踪控制问题的滚动时域控制法(Receding Horizon Control,RHC,也被称为MPC),并对其可行性和稳定性进行了严格分析.但是在文献[22]中要求每一个跟随AUV都可以与领航AUV通信,随着编队规模增大,由于首尾距离增大,跟随AUV可能无法保证与领航AUV的通信,因此该通信拓扑结构限制该方法的应用场景为小规模的编队控制.另外,阻碍DMPC方法实际应用的一个重要因素是求解完整非线性系统对应的高维问题的复杂度,降低了控制器的实时性.
本文的贡献可总结如下:
1)针对多AUV的纵向速度与深度协同控制问题,考虑AUV局部通信,设计了基于DMPC的多AUV纵向速度与深度控制方法.相比于LI等[24],该方法同时考虑纵向速度和深度的变化,实现纵向速度和深度的联合优化控制.
2)针对单AUV纵向速度和深度控制系统的状态耦合导致计算效率低的问题,提出了一种可以解耦两个系统的双子系统控制方法.在DMPC框架下,纵向速度控制子系统和深度控制子系统相互共享参考轨迹信息,以实现多变量解耦.仿真结果表明,与整体系统方法相比,本文提出的双子系统方法在减少计算量、提高实时性的同时具有满意的控制效果.
1AUV建模
1.1运动学和动力学建模
AUV的六自由度动力学模型具有多变量耦合和非线性的特征[25],给控制器设计带来了很大的挑战. 为了在模型精度、控制性能和计算效率之间达到更好的平衡,可以根据实际应用场景对六自由度动力学模型进行简化.如Zhou等[14]将六自由度动力学模型分为三个运动控制子系统:航向控制子系统、纵向速度控制子系统和深度控制子系统.
深度控制子系统可以描述为[14,26]:
纵向速度控制子系统可以表述为[14]:
在实际情况中,许多AUV并不为深度控制配备垂向推进器,深度主要依靠舵角来控制,所以垂向速度可以假设为零,则深度控制子系统可以简化为[14]
纵向速度子系统可以简化为[14]:
公式(3)和公式(4)通过纵向速度u和俯仰角θ耦合在一起,双子系统DMPC方法中两个子系统可以互相交换耦合变量的参考轨迹序列,从而解耦两个子系统.将公式(3)和公式(4)整理为整体模型以作为双子系统DMPC方法的对比:
以上述整体模型作为AUV计算优化问题和更新系统状态的模型是一种普遍使用的方法,为与本文提出的双子系统DMPC方法区别,称之为整体系统DMPC方法.
1.2通信拓扑建模
其中,N代表所有跟随AUV的数量,(j,i)∈ε则a=1,表示AUV,可以从AUVj获得信息.
其中,如果(0,i)∈ε,则p=1表示AUVi能够接受领航AUV的信息,否则p=0表示AUV,不能接受领航AUV的信息.
由于本文的研究重点为多AUV的协同运动控制,此处假设AUV的通信不存在延时和丢包现象.关于通信失效和延时方面的研究,可以参考Li等[27]和Bernardo等[28].
2AUV控制器设计
2.1多AUV系统的控制目标
在本文考虑场景中,希望跟随AUV精确地跟踪领航AUV的运动,随着时间趋近于无穷,跟随AUV 与领航AUV之间的纵向速度和深度误差应收敛于零,即:
2.2优化问题的设计
对于AUV的深度控制子系统,定义优化问题P:
约束条件为:
其中,公式(12)是对初始时刻状态的约束,要求预测状态的初值与当前实际状态值相等;公式(13)是对预测状态的约束,要求预测状态按照AUV的动力学模型计算;公式(14)和(15)是对状态和输入的约束;
对于AUV的纵向速度控制子系统,定义优化问题P:
约束条件为:
纵向速度控制子系统的约束条件和代价函数设计的思路和深度控制子系统一致,具体意义可参考上文的叙述.
2.3双子系统DMPC算法设计
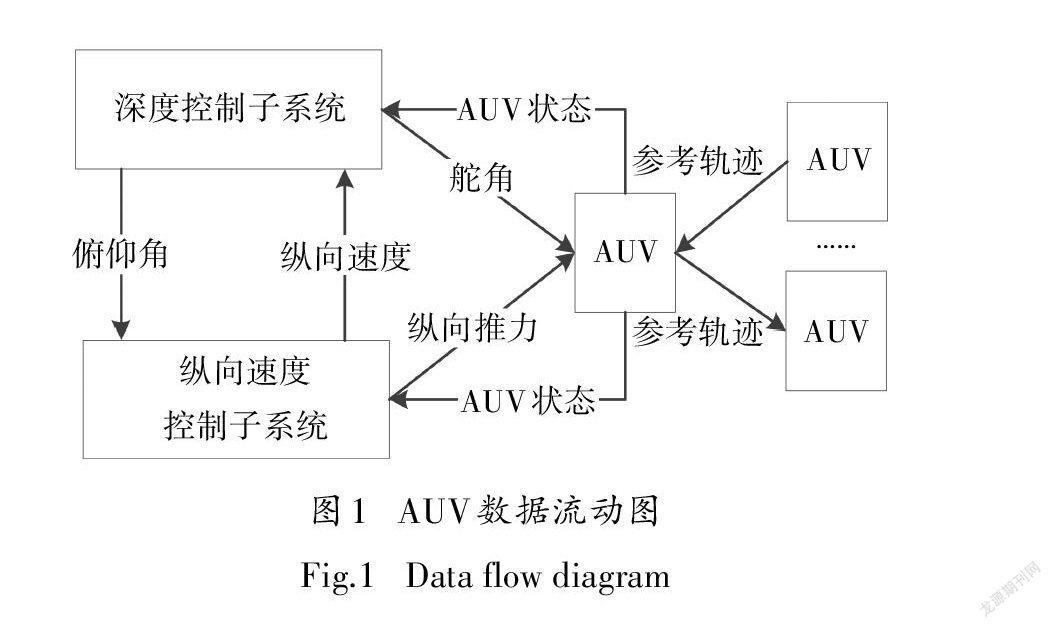
双子系统DMPC算法(表1)设计的目的在于实现两个子系统之间的数据传输、独立求解优化问题以及DMPC框架下各个AUV之间的协同.如图1所示,由于每一时刻都需要计算优化问题,所以在每一个采样时刻t(t>0),AUV的深度和纵向速度两个控制子系统分别传输参考轨迹中的俯仰角和纵向速度序列到对方,实现两个子系统解耦,这两个子系统在计算方面是独立的,并且可以部署于同一硬件设备,从而拥有相同的CPU时钟与存储
此处只给出了双子系统DMPC算法,整体系统DMPC算法和双子系统算法仅在子系统传输数据、求解优化和状态更新上有差异,其余的过程一致,可以参考Li等[24].
3仿真实验验证
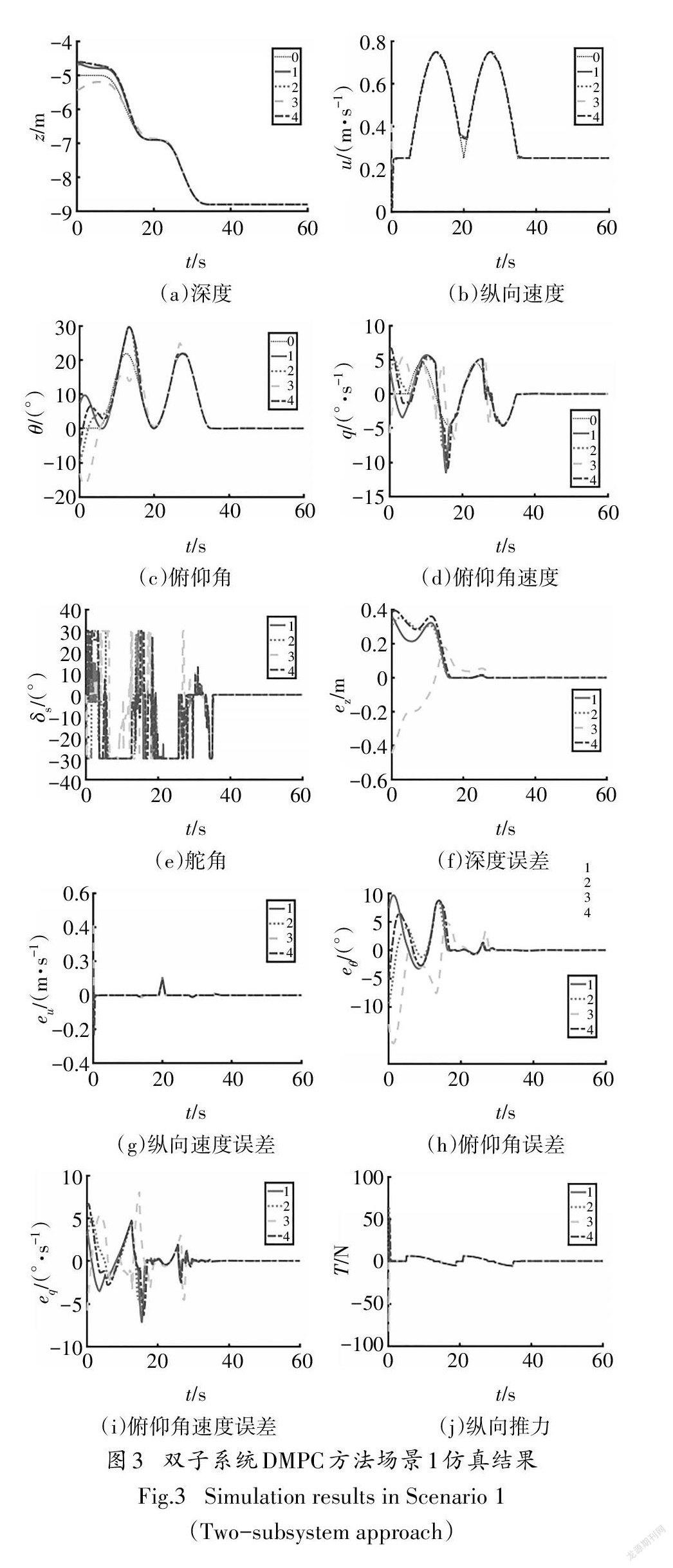
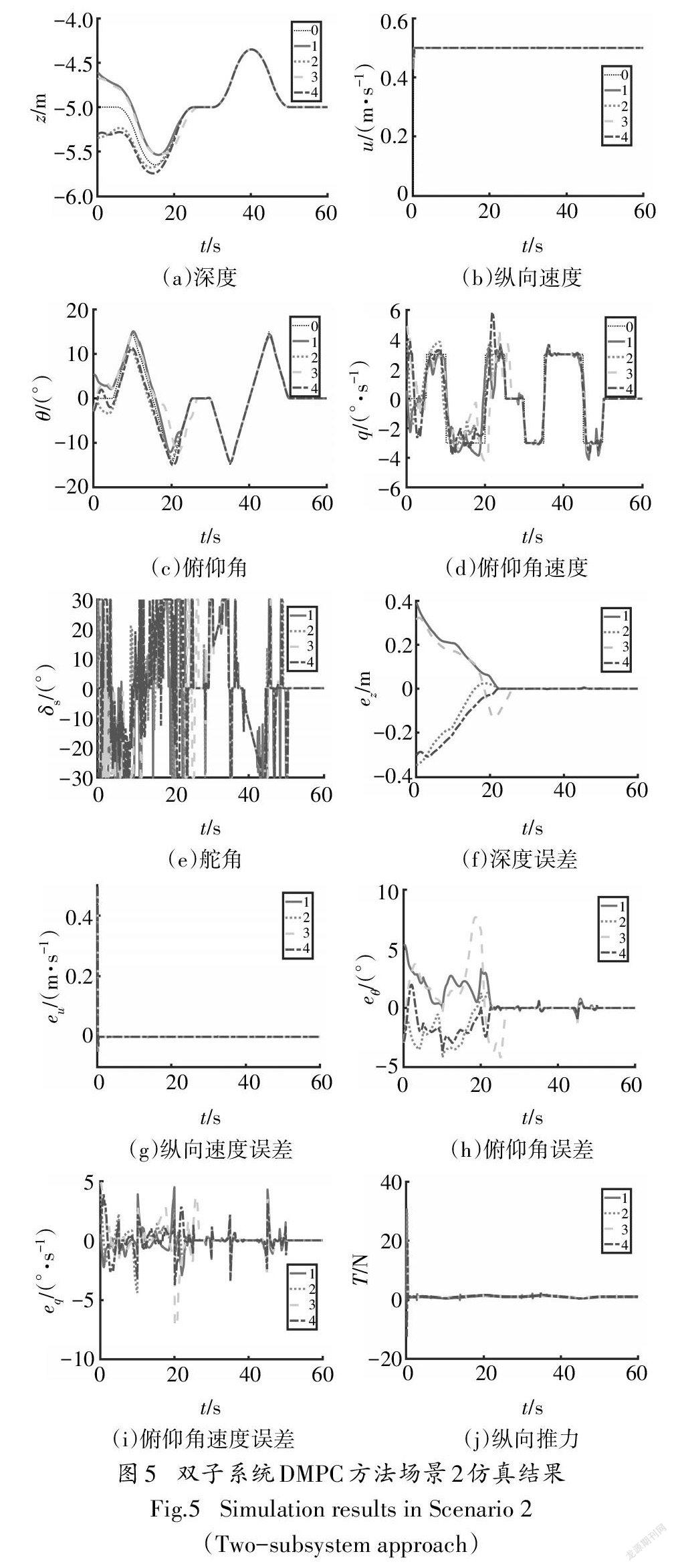
为验证双子系统DMPC方法的有效性,设计了两个仿真场景,并在场景1下对比了双子系统DMPC方法与整体系统DMPC方法的计算时间和控制性能.图2表示AUV之间的通信拓扑,表2列举了模型与控制参数,部分参考自Lapierre等[29]的工作.仿真计算平台为PC(CPU:Intel Core i5-7300HQ 2.50GHz,GPU:Nvidia GeForce 1050,RAM 8 GB).特別地,这里采用MATLAB的FMINCON函数进行原始优化问题的直接求解.这里未对求解过程进行单独优化,但对两种方法计算效率的对比仍然是具有意义的.图3-5中每一幅图中(a)~(d)表示各个AUV状态随时间的变化,(f)~(i)各跟随AUV与领航AUV的状态误差随时间的变化,(e)和⑴分别代表跟随AUV的舵角和纵向推力随时间的变化.
为了在计算时间和控制效果方面将双子系统DMPC方法与整体系统DMPC方法作对比,定义优化问题P:
约束条件为:
该方法与双子系统DMPC方法的区别在于更新状态和建立预测优化问题都依赖于耦合模型(5),需在一个优化问题中求解两类控制量.
3.1仿真场景1
仿真场景1验证多AUV在速度频繁变化与下潜时的跟踪性能.所有跟随AUV在随机初始误差下跟踪领航AUV,其俯仰角速度和纵向速度设定为:
如图3所示,在双子系统DMPC方法下,所有跟随AUV的深度[图3(a)(f)]、纵向速度[图3(b)(g)的俯仰角[图3(c)(h)]和俯仰角速度[图3(d)(i)]均可跟踪领航AUV,在状态稳定后,所有跟随AUV和领航AUV的误差趋近于零,满足控制目标.因此,双子系统DMPC方法的控制性能符合要求.
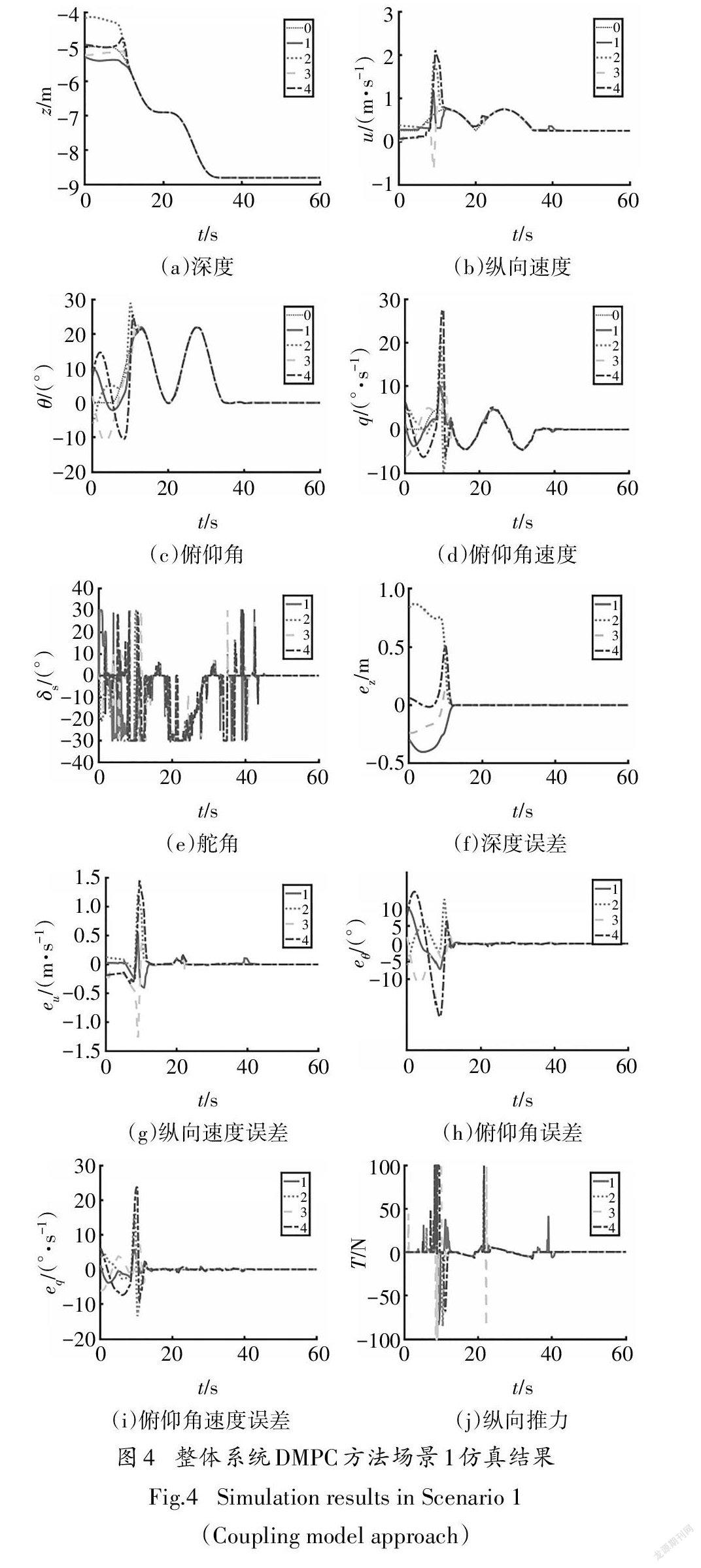
图4为整体系统DMPC方法场景1下的仿真结果.在整体系统DMPC方法下,所有跟随AUV和领航AUV的状态误差趋近于零,也满足控制性能要求.
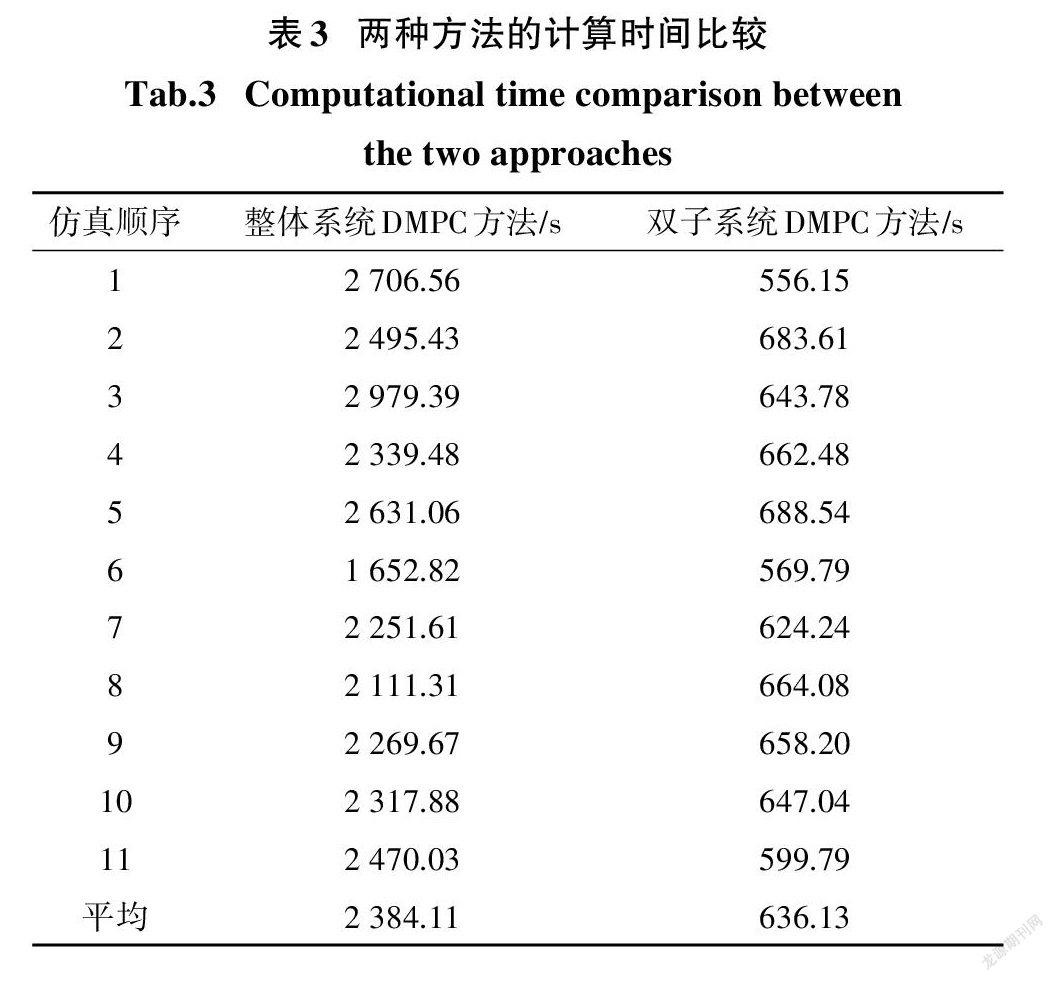
为比较两种方法的计算效率和控制效果,在相同的条件下对两种方法进行了11次仿真,两种方法的总计算时间如表3所示.双子系统DMPC方法的平均计算时间为636.13 s,整体系统DMPC方法的平均计算时间为2 384.11s.比较整体系统DMPC方法和本文提出的双子系统DMPC方法,由于双子系统DMPC方法解耦了两个子系统,分别求解两类控制量,使单次求解优化问题的变量维度变小,计算时间由此降低了73.3%.此外,在本仿真实验中,两个优化问题串行求解,而在实际应用中,双子系统DMPC方法可通过并行求解两个子系统的优化问题,进一步提高计算效率.
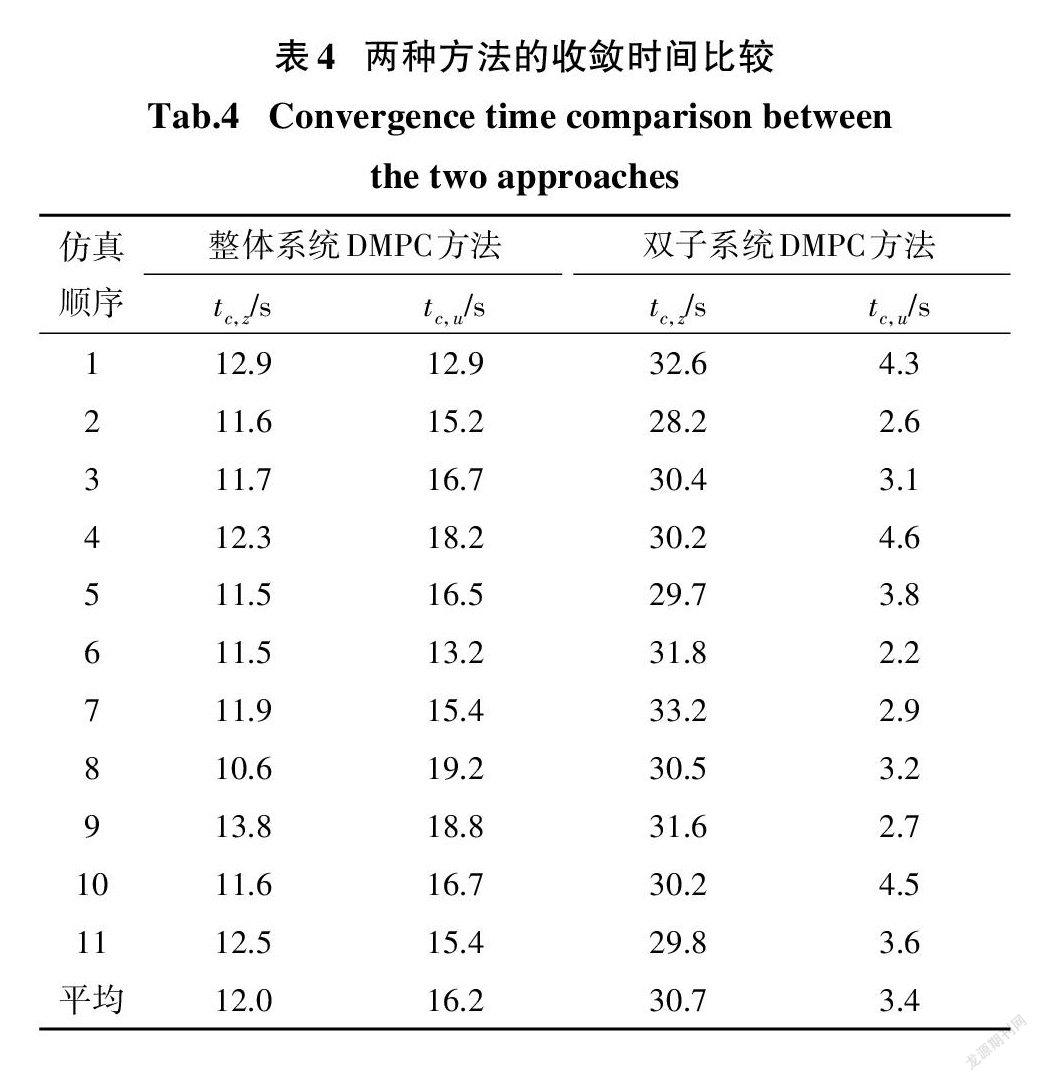
为比较两种方法的控制性能,定义收敛时间t和t为所有的跟随AUV与领航AUV纵向速度和深度误差第一次收敛到零的时间.两种方法的收敛时间如表4所示.采用双子系统DMPC方法和整体系统DMPC方法的平均深度收敛时间分别为30.7 s和12.0 s,平均纵向速度收敛时间分别为3.4 s和16.2 s. 在双子系统DMPC方法中,由于假设状态与真实的未来状态存在偏差,会对计算精度有一定影响,但是模型预测控制本身具有鲁棒性特点,并且从仿真结果上看,双子系统DMPC方法具有更好的纵向速度控制性能,虽深度控制性能有所下降,考虑到计算时间的大幅降低(73.3%),在某些应用情况下适当牺牲深度控制性能是可以接受的.
3.2仿真场景2
仿真场景2验证多AUV在行进过程中避开障碍物的能力.跟随AUV在随机初始误差下跟踪动态领航AUV,其纵向速度为恒定值0.5m/s,俯仰角速度为:
在垂直平面上做正弦运动是检验深度控制子系统控制性能的一种有效方法.如图5所示,跟随AUV在第一次下潜(t<20s)时与领航AUV在深度上有误差,但是在第一次上升(25s<t<35s)时,误差接近于0,由此说明AUV可以协同上升、下潜从而规避障碍物.其余状态量的误差也在状态稳定后趋近于0,达到控制目标.因此,双子系统DMPC方法符合控制要求.
4结论
本文研究了多AUV的深度和纵向速度控制问题,将多变量耦合非线性复杂模型分解为两个子系统,即纵向速度控制子系统和深度控制子系统.基于DMPC方法,多AUV系统中各个单AUV的两个控制子系统相互传输必要的数据,即俯仰角和纵向速度,使得两个子系统解耦,从而获得更好的计算效率.然后,设计了局部开环优化问题,并分别求解优化问题得到最优控制输入.通过不同场景下的数值模拟,验证了该方法的有效性.本研究的一个延伸是严格分析所提出方法的稳定性.另外,传递给另一个子系统的假设轨迹只迭代一次,应多次迭代假设轨迹,直到误差在一个合适的范围,从而更好地平衡控制效果与计算效率.
参考文献
[1] LI X,ZHU D Q,QIAN Y A. A survey on formation control algorithms for multi-AUV system [J]. Unmanned Systems,2014,2 (4):351-359.
[2] SHIL L,ZHENG RH,LIUMQ,et al. Cooperative flow field estimation using multiple AUVs [C]//2020 59th IEEE Conference on Decision and Control. December 14-18,2020,Jeju,Korea (South). IEEE,2020:5243-5248.
[3] XU B,GUO Y,WANG L Z,et al. A novel robust Gaussian approximate smoother based on EM for cooperative localization with sensor fault and outliers [J]. IEEE Transactions on Instrumentation and Measurement,2021,70:1-14.
[4] CUI R X,YANG C G,LI Y,et al. Adaptive neural network control of AUVs with control input nonlinearities using reinforcement learning[J].IEEE Transactions on Systems,Man,and Cybernetics:Systems,2017,47(6):1019-1029.
[5] FIORELLI E,LEONARD N E,BHATTA P,et al. Multi-AUV control and adaptive sampling in Monterey Bay[C]//IEEE Journal of Oceanic Engineering.IEEE,:935-948.
[6] SURYENDU C,SUBUDHI B.Formation control of multiple autonomous underwater vehicles under communication delays[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2020,67(12):3182-3186.
[7] YAN Z P,WU Y,LIU Y B,et al.Leader-following multiple unmanned underwater vehicles consensus control under the fixed and switching topologies with unmeasurable disturbances[J].Complexity,2020,2020:1-26.
[8] GAO Z Y,GUO G.Fixed-time sliding mode formation control of AUVs based on a disturbance observer[J].IEEE/CAA Journal of Automatica Sinica,2020,7(2):539-545.
[9] ROUT R,SUBUDHI B. A backstepping approach for the formation control of multiple autonomous underwater vehicles using a leader-follower strategy [J]. Journal of Marine Engineering & Technology,2016,15(1):38-46.
[10] SAHU B K,SUBUDHI B.Flocking control of multiple AUVs based on fuzzy potential functions[J].IEEE Transactions on Fuzzy Systems,2018,26(5):2539-2551.
[11] WANG H L,WANG D,WANG T L,et al.Adaptive cooperative diving of saucer-type underwater gliders subject to model uncertainties and input constraints[J].IEEE Access,2019,7:60042- 60054.
[12] WANG J Q,WANG C,WEI Y J,et al.Neuroadaptive sliding mode formation control of autonomous underwater vehicles with uncertain dynamics[J].IEEE Systems Journal,2020,14(3):3325- 3333.
[13] YAO F,YANG C,LIU X,et al.Experimental evaluationon depth control using improved model predictive control for autonomous underwater vehicle(AUVs)[J].Sensors(Basel,Switzerland),2018,18(7):2321.
[14] ZHOU H Y,LIU K Z,FENG X S.Selected optimal control from controller database according to diverse AUV motions[C]//2011 9th World Congress on Intelligent Control and Automation.June 21-25,2011,Taipei,Taiwan,China.IEEE,2011:425-430.
[15] KHODAYARI M H,BALOCHIAN S.Design of adaptive fuzzy fractional order pid controller for autonomous underwater vehicle (auv)in heading and depth attitudes[J].International Journal of Maritime Engineering,2021,158(A1):31-48.
[16] WU H,SONG S J,YOU K Y,et al.Depth control of model-free AUVs via reinforcement learning[J].IEEE Transactions on Systems,Man,and Cybernetics:Systems,2019,49(12):2499-2510.
[17] NURHADI H,HERLAMBANG T,SUBCHAN.Design of sliding mode control for surge,heave and pitch motion control of UNUSAITS AUV[C]//AIP Conference Proceedings","the 4th biomedical engineering's recent progress in biomaterials,drugs de- velopment,health,and medical devices:Proceedings of the International Symposium of Biomedical Engineering (ISBE)2019. Padang,Indonesia.AIP Publishing,2019:2019
[18] ZHENG Y,LI S E,LI K Q,et al. Distributed model predictivecontrol for heterogeneous vehicle platoons under unidirectional topologies[J]. IEEE Transactions on Control Systems Technology,2017,25(3):899-910.
[19] NEGENBORN R R,MAESTRE J M. Distributed model predictive control:an overview and roadmap of future research opportunities[j]. IEEE Control Systems Magazine,2014,34(4):87-97.
[20] DUNBAR W B,CAVENEY D S. Distributed receding horizon control of vehicle platoons:stability and string stability[J]. IEEE Transactions on Automatic Control,2012,57(3):620-633.
[21]孫浩,杜煜,卜德旭,等.汽车轨迹跟踪模型预测控制的加速求解方法[J].湖南大学学报(自然科学版),2020,47(10):19-25.
SUN H,DU Y,BU D X,et al. Accelerated solution method for vehicle trajectory tracking based on model predictive control [J]. Journal of Hunan University(Natural Sciences),2020,47(10):19-25.(In Chinese)
[22] LI H P,XIE P,YAN W S. Receding horizon formation tracking control of constrained underactuated autonomous underwater vehicles[J].IEEE Transactions on Industrial Electronics,2017,64 (6):5004-5013.
[23] SHEN C,SHI Y,BUCKHAM B. Trajectory tracking control of an autonomous underwater vehicle using Lyapunov-based model predictive control[J].IEEE Transactions on Industrial Electronics,2018,65(7):5796-5805.
[24] LI C K,BIAN Y G,ZHANG J J,et al. Distributed model predictive control for cooperative diving of multi-AUV systems [C]//2020 4th CAA International Conference on Vehicular Control and Intelligence(CVCI).December 18-20,2020,Hangzhou,China.IEEE,2020:169-174.
[25] YILDIZ O,GOKALP R B,YILMAZ A E.A review on motion control of the Underwater Vehicles [C]//2009 International (Conference on Electrical and Electronics Engineering —ELECO 2009. November 5-8,2009,Bursa,Turkey.IEEE,2009:II-337.
[26] FOSSEN T I. Guidance and control of ocean vehicles [J]. Automatica,1996,32(8):1235.
[27] LI K Q,BIAN Y G,LI S E,et al. Distributed model predictive control of multi-vehicle systems with switching communication topologies[J].Transportation Research Part C:Emerging Technologies,2020,118:1-18.
[28] DI BERNARDO M,SALVI A,SANTINI S.Distributed consensus strategy for platooning of vehicles in the presence of time-varying heterogeneous communication delays[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(1):102-112.
[29] LAPIERRE L.Robust diving control of an AUV[J].Ocean Engineering,2009,36(1):92-104.
