一次提升“四能”的探究之旅
——从一道三角不等式的教学谈起*
2022-11-14李勤俭安徽省池州市第一中学247000
李勤俭 (安徽省池州市第一中学 247000)
在高中数学教学中,教师有意识地引导学生进行思考,从数学角度发现和提出问题、分析和解决问题,不仅是新课程标准的要求,也能高效地提高学生自主学习的能力.本文从一个正弦定理推证过程中得到的三角不等式入手,探讨如何在解题教学中提升学生的“四能”.
1 发现问题,提出问题
2 分析问题,问题解决
不等式①的左边看起来比较正常,但右边就让人难以接受.看到π,联想到几何意义,所以从圆入手也算自然;①式是代数式,理应有代数证法,那么作为三角函数式,可以从三角变换角度去解决;同时,从式子的结构出发,可以看成是余弦函数相关问题,所以从函数角度分析应该也能解决问题.
2.1 几何证法
在图1中,圆O是△ABC的外接圆.下面分△ABC是锐角三角形、直角三角形和钝角三角形三种情形证明.

图1 图2
证明(1)当△ABC是锐角三角形时,如 图2,连结BO,AO并延长分别交圆O于点E,F,再连结BF,FC,CE,EA,则BF=2RcosC,FC=2RcosB,BD=2RcosA.

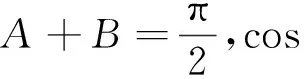
(3)当△ABC是钝角三角形时,不妨设C>90°,此时可将图2中的点D与点C对换,转化为情形(1),得证.
几何证法直观、好理解,但不容易想到.我们再尝试用代数证法.
2.2 代数证法
先证cosA+cosB+cosC>1 ②.
因为cosA+cosB+cosC



为了证④式,先证下式:

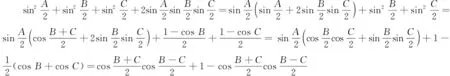
另一方面,在⑤式中,有如下变形:
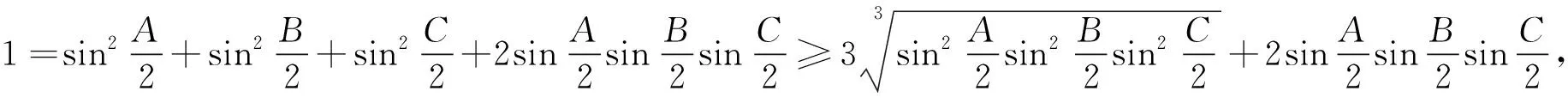
由②④可得①式得证.
由此还可以顺带得①式的加强式:

2.3 琴生不等式证法
琴生不等式(Jensen Inequality):
函数f(x)是定义在开区间(a,b)上的凸函数.设λ1,λ2,…,λn是n个正实数,且λ1+λ2+…+λn=1,x1,x2,…,xn是开区间(a,b)上任意n个点,则下面不等式成立:f(λ1x1+λ2x2+…+λnxn)≥λ1f(x1)+λ2f(x2)+…+λnf(xn).这个不等式称为琴生不等式.(注意:对于凹函数(下凸函数),上式中的“≥”变为“≤”)

3 再次提出问题
一个问题从提出到解决,并不是思维过程的结束,而往往是新问题的开始.①式是针对余弦函数而言的,那么对于正弦函数、正切函数,相应的结论是什么?又如何证明?
3.1 与正弦函数有关的不等式
经过探讨分析得到


3.2 与正切函数有关的不等式
当△ABC是锐角三角形时,

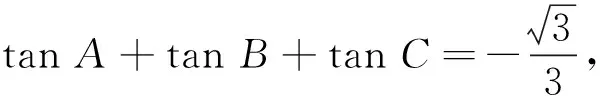

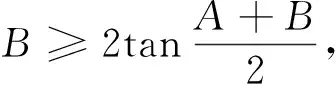




4 几点感悟
在学习数学的过程中,发现问题往往比证明结论更重要.《普通高中数学课程标准(2017年版)》提出了“四能”[2],因此教师需要适时、适度地引导学生发现、提出一些数学问题,进而分析和解决问题,促进学生数学水平的提高.
(1)引导学生学会提出问题的方法应成为教学中的一个重要内容.本文由余弦函数的一个优美的不等关系,运用合情推理的方法拓展到了与正弦和正切函数相关的性质.如何引导学生学会提出问题,也许比帮助学生解决问题更有意义.
(2)对一个问题的解决进行多角度思考是数学探究的基本思路.文中对不等式①的证法进行了多角度的思考,得到了很好的思维体验.这意味着教师在教学过程中如何进行多角度的思考,以及如何引导学生多角度思考是值得探索的一个课题.
(3)要在解决问题的过程中进行逻辑推理等核心素养的培养.本文在探讨的过程中,包含了很多较深刻的分析与推理,使得学生在过程中学习,在过程中提高.
(4)探究无止境.文中通过探究得到了八个关系式,它们的应用又可作为新的探讨课题.
在这一探讨的旅程中,学生得到了很好的思维能力的训练,以及分析问题和解决问题的能力训练,体会到数学的严谨美、和谐美,提高了学习数学的兴趣.这不正是新课程理念所要求的吗?
