基于DCC-2D的电动汽车充电站时空动态负荷预测

2022-11-14杨京渝蒋天香李佳亮林之怡

湖南城市学院学报（自然科学版） 2022年6期

彭丽，杨京渝，蒋天香，李佳亮，曹健，林之怡

(湖南城市学院智慧城市能源感知与边缘计算湖南省重点实验室，湖南益阳 413000)

我国明确提出的“碳达峰、碳中和”战略目标，为推动先进环保、先进储能等绿色低碳新技术的不断成熟，打造绿色低碳领域的竞争优势提供了新空间[1-2].电动汽车因能从源头上解决环境污染、缓解不可再生能源的短缺、减少CO2排放等问题，获得了广泛关注和积极推广[3-4].然而，大规模的电动汽车接入和无序充电给城市电网带来的冲击也与日俱增，影响了电力系统的安全稳定运行[5].因此，提高电动汽车充电桩负荷预测的精度，可以更好地指导电网运行、调度等工作，有效消除电动汽车充电给电网带来的负面影响，具有重要的理论与实际意义.

目前，国内外学者已在电动汽车充电站负荷预测上做了较多相关研究.电动汽车充电站负荷预测手段主要可分为模型驱动方法和数据驱动方法2 大类[6].模型驱动方法是通过建立数学模型来模拟电动汽车充电的时空分布特性，如文献[7]提出了一种新型的Sigmoid 云模型，该模型能更准确地描述电动汽车用户收益与响应行为之间的不确定关系，预测信息更为全面；文献[8]提出了充电负荷时空分布的模拟方法，创建了充电站吸引力模型，提出了交通耗时指数概念，实现了充电站负荷时空分布的模拟.模型驱动方法虽然具有较好的可解释性和通用性，但数学模型的创建往往太过复杂，难以保证预测精度.

数据驱动方法基于充电站实际历史数据，采用统计学习法建立预测模型，相比于模型驱动方法，其预测结果更接近于真实值的变化趋势.传统的充电站负荷预测方法有相似日法、回归分析法等[9-10].随着人工智能的发展，BP 神经网络(back propagation neural network，BPNN)、支持向量机(support vector machine，SVM)、长短时记忆神经网络(long short term memory，LSTM)、卷积神经网络(convolution neural networks，CNN)等现代预测方法均取得了较好的建模预测效果[11-13].文献[14]提出了采用支持向量机的电动汽车充电站短期负荷预测方法；文献[15]研究了数据新鲜度和交叉熵相结合的组合预测方法；文献[16]采用经验模态分解(empirical mode decomposition，EMD)对原始充电负荷进行分解，经模糊熵计算各分量的复杂度后得到一系列子序列，再通过LSTM 和回归支持向量机(support vector regression，SVR)分别对高频和中低频分量进行预测.但以上研究大多只考虑时间维度上的预测，重点关注时间维度信息的挖掘，忽略了复杂的空间维度信息潜在的影响，因此限制了模型的预测精度.

为了更好地进行电动汽车充电负荷时空动态预测，提高其预测精度，本文提出了一种基于DCC-2D 的电动汽车充电站时空动态负荷预测方法.首先，为了使模型能够学习到空间维度信息，通过向三维卷积添加空洞因子构建二维空洞卷积层；其次，将二维空洞卷积层堆叠以构成整个二维卷积神经网络，使得模型可以学习到时间维度信息；最后，以某市充电站负荷数据为例，实验验证所提模型的正确性和优越性.

1 时空卷积神经网络模型

1.1 一维空洞因果卷积

单纯的因果卷积对时间的建模长度受限于卷积核的大小，为了捕获长期的依赖关系，需线性地堆叠较多的层数.为了尽量减少堆叠层数，可采用堆叠空洞卷积层的结构.该结构输出层的特征映射如式(2)所示.

图1 一维空洞卷积神经网络示例

1.2 三维卷积

二维卷积只能捕捉到空间维度的信息.式(3)表示二维卷积神经网络第i层中第j卷积核(x,y)的卷积结果.

2 基于DCC-2D 的充电站负荷预测模型

2.1 基于DCC-2D 的充电负荷预测流程

一维空洞因果卷积神经网络是主要考虑时间维度信息的预测方法，而电动车充电站负荷具有时空动态特性，一维空洞卷积无法满足其预测精度要求.因此，将一维空洞卷积的一维卷积替换为三维卷积，构建二维空洞因果卷积神经网络.其卷积过程如式(5)所示，感受野的大小r如式(6)所示，其中R表示三维卷积核中第一维的大小.

所提模型的整个预测流程如图2 所示.

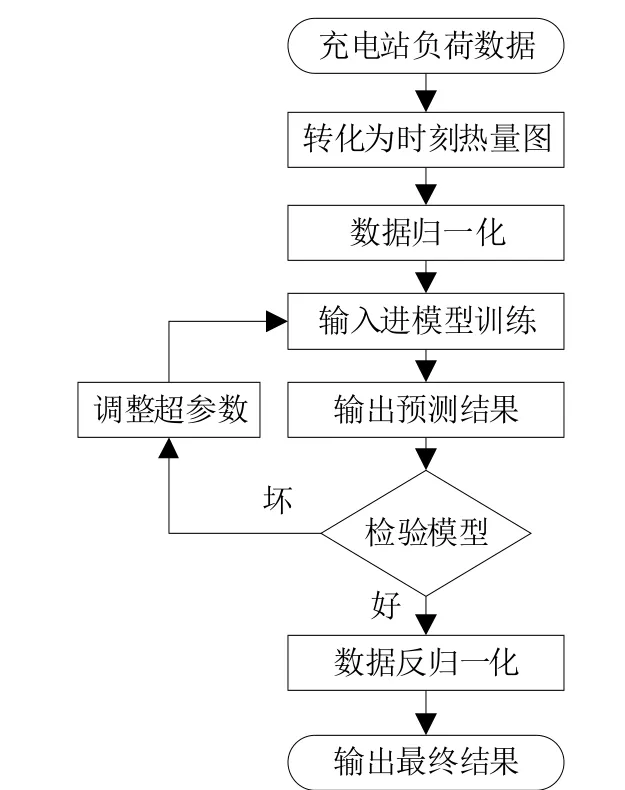
图2 模型预测流程

1)根据充电站位置建立充电站的平面分布图，完成充电负荷时空维度的刻画.

2)根据充电站历史负荷数据，按时间顺序将各站点在平面分布图上画成热量图.

3)对热量图的数据进行归一化处理.

4)将数据输入预测模型进行训练，再根据预测结果的好坏调整预测模型的超参数，直至模型训练达到理想的效果.

5)将所得数据进行反归一化处理，得到最后的预测结果.

2.2 评价指标

充电站充电负荷预测的评价指标包括：1)可决系数R2(R-squared)

3 算例仿真分析

3.1 仿真参数设置

为了验证所提预测方法的正确性和优越性，本文将STN 预测模型与所提模型进行了对比.实验选取我国某城市10 个充电站的实际充电负荷数据进行仿真.数据采样频率为1 条/h，将过去300 h 的充电负荷数据作为训练集，滚动预测未来24 h 的充电站负荷.实验选择在TensorFlow 平台上进行，其硬件环境为：CPU，i7-7000；GPU，1050Ti 4 G；内存，16 G.

3.2 预测结果与分析

分别采用DCC-2D 和STN 2 种预测模型对充电站未来24 h 的充电负荷进行了预测，其结果如图3 所示.

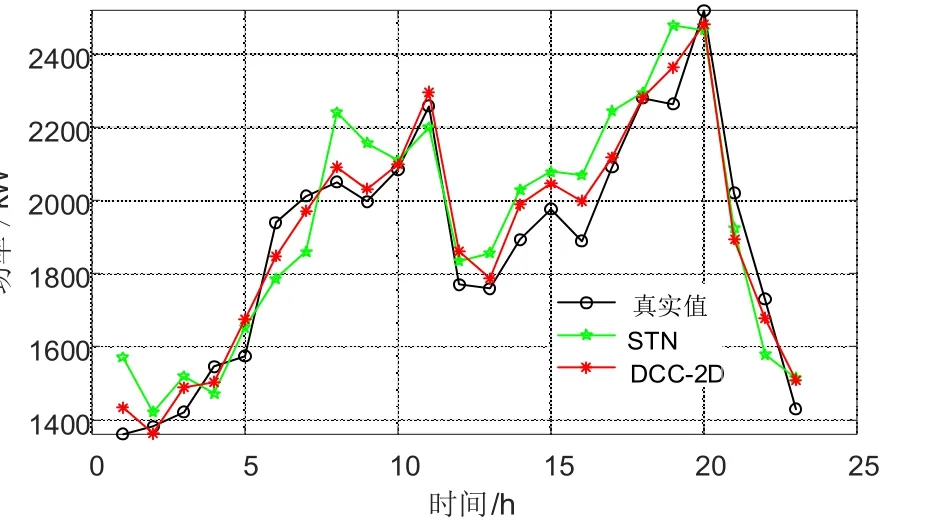
图3 各模型预测结果对比

由图3 可以看出，DCC-2D 模型的预测结果更加贴近真实值变化趋势，相比STN 模型有较明显的优势.

表1 给出了DCC-2D 和STN 2 个预测模型在3 次实验中的eMAE、eMSE和R²评价指标数据及其对应的平均值.

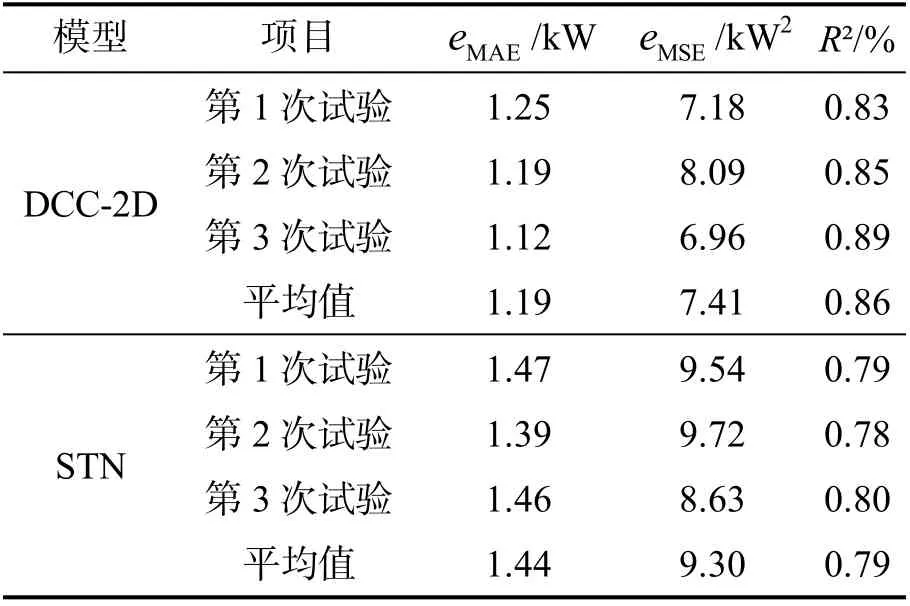
表1 预测结果误差评价指标

由表1 可知，DCC-2D 预测模型的eMAE和eMSE平均值比STN 预测模型分别下降了0.25 kW 和1.89 kW2，其降幅分别为17.36%和20.32%；DCC-2D 的R²平均值比STN 提升了0.07%.由此可知，DCC-2D 模型比STN 模型具有更高的预测准确率.这说明本文所提方法能够提高电动汽车充电负荷的预测精度.