交通荷载和锚杆相对位置对锚固边坡动力承载特性影响研究

2022-11-14张根宝付贵海谢晨风黄道吉

湖南城市学院学报（自然科学版） 2022年6期

张根宝，付贵海，谢晨风，张昱，黄道吉

(1. 湖南城市学院土木工程学院，湖南益阳 413000；2. 城市地下基础设施结构安全与防灾湖南省工程研究中心，湖南益阳 413000；3. 莆田市城厢区城乡建设投资集团有限公司，福建莆田 351100；4. 中国建筑第五工程局有限公司总承包公司，长沙 410000)

锚固边坡是交通基础设施建设中的重要岩土支护技术.在山区高速公路和高速铁路沿线广泛分布着各种锚固边坡应用场景，其包括但不限于挖方区边坡、隧道口边坡、桥台边坡以及路堤边坡等[1-2]，如图1 所示.上述锚固边坡在服役过程中不可避免地经受来自轮轨振动等交通荷载作用，为了对此类锚固边坡进行更科学地设计计算，需要准确掌握其动力承载特性随交通荷载作用参数变化的演化模式[3-4].目前，关于锚固边坡的动力响应研究多为地震作用影响[5-8].如2011 年，朱宏伟等[5]通过现场测试验证了锚杆支护可有效提高地震作用下边坡的动力稳定性；2018 年，言志信等[6]通过数值仿真系统地研究了地震作用下锚杆长度和直径等锚固参数对边坡锚固界面剪应力分布和锚固机理的影响.关于交通荷载作用的影响研究多集中在路基减震隔振效果[9-13].如2012年，Çelebi 等[9]通过有限元数值模拟研究了交通荷载引起的振动在设有阻波带的铁路路基中的传播特性.关于交通荷载对边坡承载性能影响的研究相对较少[14-15].如2006 年，樊秀峰等[14]通过现场振动响应测试发现无支护公路边坡的振动响应对交通荷载较为敏感；2014 年，Connolly 等[15]对高速铁路振动进行了现场测试，发现交通荷载与路基在不同相对位置下，路基动力响应存在明显差异.目前，关于交通荷载和锚杆的空间相对位置对锚固边坡动力响应影响的研究鲜有文献报道，交通荷载和锚杆锚固空间分布差异对边坡承载性状的耦合影响机理依然不明确，需要开展专门研究.此外，锚固边坡动力特性研究往往涉及荷载作用参数和锚固参数等多源多维参数，采用动力加载模型进行试验研究对试验模型的工况数量要求较高[16]，试验经济性面临挑战；数值试验平台已成为参数影响研究的重要且有效的方法[17].

图1 交通荷载作用下锚固边坡典型应用场景

鉴于上述研究现状，本文针对交通荷载作用下锚固边坡动力承载特性，特别是荷载和锚杆空间分布对其影响的规律，进行了数值试验研究.试验工况包括交通荷载相对坡体位置和坡体内锚杆位置，承载特性评估主要采用加载周期内边坡坡脚位移、边坡坡顶位移、锚杆锚头锁固力、锚杆轴力与界面剪应力等指标.需要说明的是，为了确保数值模拟结果可以准确反映锚杆空间效应，避免群锚效应和尺寸效应等因素对分析结果的耦合影响，本文在数值试验中只调整单根锚杆在坡体影响区域内的相对位置，不改变锚杆尺寸和倾角等锚固参数.

1 数值试验方案设计

考虑到实际工程中交通荷载作用下锚固边坡主要受到外部荷载和内部锚固体的时空效应影响，本文着重考察交通荷载在边坡的相对作用位置和锚杆在坡面的相对设置位置2 种典型工况，并结合实际运维中锚固边坡的主要病害统计[2]，考虑锚杆锚固力变化与坡体变形存在的复杂耦合关系[18]，将边坡变形和锚杆受力作为主要关注点.边坡变形通过坡顶位移和坡底位移2 个指标定量分析，锚杆受力则通过锚头锁固力、锚杆轴力和锚固界面剪应力等指标进行定量分析，具体工况位置和评估指标如表1 所示.

表1 数值试验工况和评估指标

2 锚固边坡数值建模

2.1 锚固边坡基准模型

本文分析基于实际工程中常见的锚固岩质边坡开展，采用岩土工程中被广泛使用的有限差分数值分析软件FLAC3D进行数值建模.为了突出工况变化下锚固边坡动力响应的差异，数值试验中设置基准模型，该模型对应表1 中交通荷载作用在坡底、锚杆布置在坡面中心的工况，其他工况可在基准模型上进行修改得到.由于本文的分析对象为在宽度方向上有对称性的锚固边坡，所以边坡坡顶和坡脚变形分别选用对称面与坡顶线和坡脚线的交点作为代表点.所建锚固边坡基准模型如图2 所示.

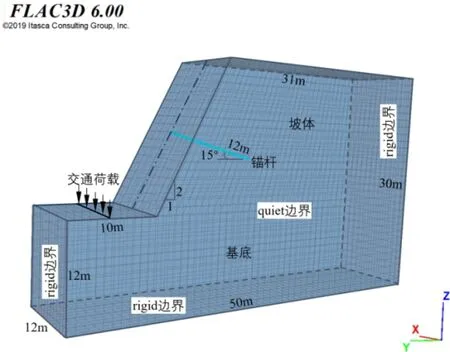
图2 锚固边坡数值基准模型

由图2 可知，锚固边坡由坡体和基底部分组成，其具体尺寸为：坡顶水平，坡高18 m，基底高12 m；坡长40 m，基底长50 m，坡脚外基底顶面为交通荷载作用区域；边坡宽度为12 m(该宽度一方面可以保证空间边界效应得以考虑；另一方面可以保证模型单元数在合理区间内).边坡锚杆全长粘结，直径150 mm，长12 m，倾角15°；锚杆设置在模型宽度方向的对称面上(以消除不对称边界效应)；锚头基准位置在坡面中心，位置高度为21 m(在后续空间布局影响分析中会改变锚头位置)；锚杆张拉预应力为100 kN.

2.2 锚固边坡材料参数

岩质边坡的岩土体均采用摩尔-库伦材料模拟；锚杆锚固体采用pile 结构单元模拟，锚固界面剪切特性采用三折线模型，界面法向约束采用理想弹塑性模型，如图3 所示.

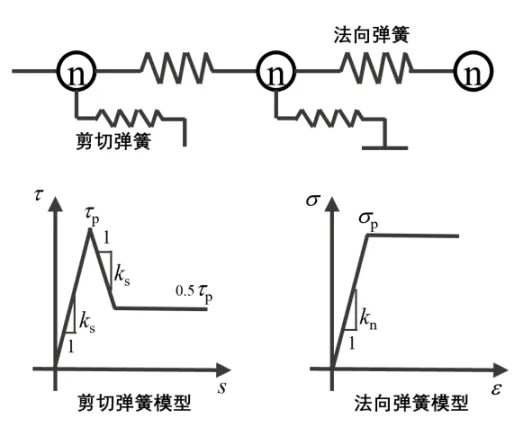
图3 基于pile 结构单元的锚固界面模型示意

根据锚固岩质边坡相关设计资料[3-4]，在合理区间内确定锚固边坡材料参数和锚杆锚固参数取值，如表2 所示.

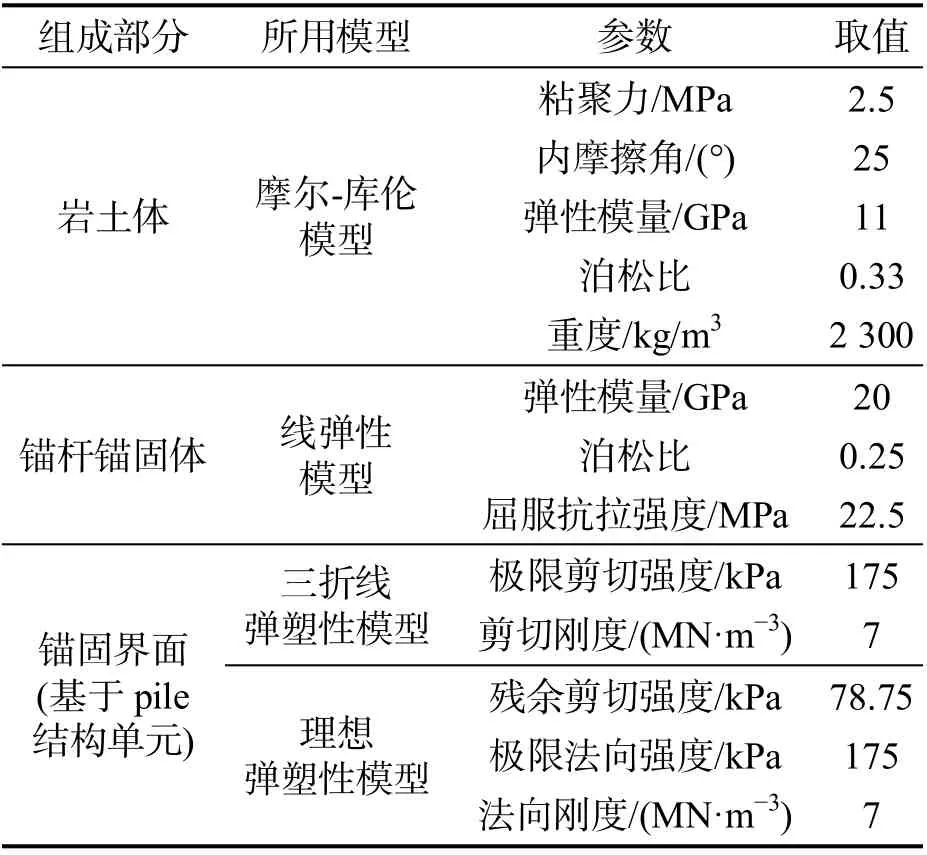
表2 锚固边坡模型参数取值

需要说明的是，pile 结构单元模拟的是锚杆锚固体，不考虑锚杆筋体与砂浆界面滑移；锚杆参数是根据锚杆锚固体截面等效刚度换算而来；文中锚固界面均指锚固体与岩土体界面.

2.3 数值模型有效性验证

为了测试FLAC3D锚固边坡数值建模中基于pile 结构单元的锚杆锚固体模型及对应的锚固界面模型的有效性，采用陈昌富等[19]获得的单元锚杆室内拉拔试验数据对其进行验证.其中，单元锚杆试样的锚固段长度为10 cm，自由段长度为5 cm，锚固体直径为3.8 cm.按照1 mm/min 的速度对锚杆杆端施加拉拔力，直至拉拔位移达到2 cm，所得锚杆杆端拉拔力-拉拔位移曲线如图4所示(实线).

图4 单元锚杆拉拔试验的数值模型验证

本文采用2.2 节中介绍的pile 结构单元模拟锚杆锚固体进行单元锚杆拉拔的数值模拟.pile结构单元的极限剪切强度取50 kPa，残余剪切强度取40.5 kPa.根据试验材料具体情况，土体剪切模量取10 MPa，锚固体弹性模量取20 GPa，锚固体泊松比取0.25.图4(虚线)给出了数值模拟得到的单元锚杆杆端拉拔响应曲线.

对比数值模拟和试验量测结果，发现二者整体趋势基本一致，锚杆拉拔响应中应力峰值前的弹塑性特征和峰值后的应变软化特征均在数值模型分析结果中得到了有效反映.因此，可以认为在FLAC3D 中采用pile 结构单元模拟锚杆锚固体及其锚固界面特性具有较好的准确性，将其进一步用于锚固边坡动力分析是可靠的.

2.4 交通荷载和模型边界

实测交通荷载引起路轨振动的加速度波形通常为复杂的不规则波[14-15]，其振幅在一定范围内随着交通工具驶近和驶离而呈现先增后减的变化趋势.因此，为了准确获取边坡动力响应与振动参数间的关系，基于实测路轨加速度波形特征[15]，采用如图5 所示的规则波形模拟交通荷载.其幅值按照余弦波型递增和衰减；作用周期为6 s，频率f为2 Hz，最大幅值A为0.2 g(g 表示重力加速度)；对应的波形函数式为：

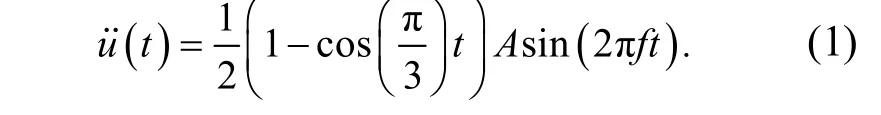
图5 交通荷载基本波形函数

值得说明的是，在交通荷载作用下锚固边坡承载特性分析属于动力响应分析，故锚固边坡模型动力边界需要进行专门设置.本文考虑到实际边坡长度方向(x方向)尺寸远大于其他2 个方向尺寸，类似平面应变问题，x方向的2 个边界均取为quiet 边界，以消除长度方向上的波反射影响；其他2个方向上的边界(除z方向的坡顶)均取法向变形约束的rigid 边界，如图2 所示.

2.5 锚杆锁固力施加

在施加交通荷载前，对锚杆锚头施加100 kN的锁固力，以模拟实际工程中锚固边坡的锚杆预应力工况.在锁固力施加过程中，锚固边坡发生了必要的变形响应，待变形稳定后，锚杆锚头锁固力为96 kN.锁固力施加过程演化和稳定后锚杆轴力分布如图6 所示.

图6 锚头锁固力施加稳定过程和锚杆轴力分布

3 基准模型计算结果

为了获得后续作用参数影响研究的比较对象，首先对交通荷载作用下锚固边坡基准模型(见图2)进行计算分析.需要说明的是，根据轨道宽度，交通荷载已被简化为宽度为2 m 的作用区域，且为了消除作用区域在作用面上的相对位置影响，在2 种试验工况下，其作用宽度中线与坡脚线和坡顶线的距离均被确定为5 m.在模型计算中，交通荷载作用时间为14 s，其中前6 s 为加速度基本波形，后续8 s 的加速度为0(见图5).根据模型的计算结果，并基于表1 中的评估指标，对基准模型对应的锚固边坡动力响应进行分析.

3.1 锚头锁固力演化

由图7 可知，当作用时间为1.5～6 s 时，锚杆锚头锁固力发生小幅振荡，振幅为95～97 kN，不到锁固力的2%；当作用时间为6～8 s 时，锁固力振幅较小；当作用时间为8～10 s 时，锁固力发生衰减并伴随振幅加大；10 s 以后，衰减停止，振幅稳定在81～87 kN，达到锁固力的6.5%，平均衰减幅度为12 kN，达到锁固力的12.5%.同时，锚杆周边土体变形径向发展，最大变形量达到5.4 mm；靠近坡脚一侧的荷载作用边界附近土体变形大于作用面下方土体变形，但均小于5 mm.

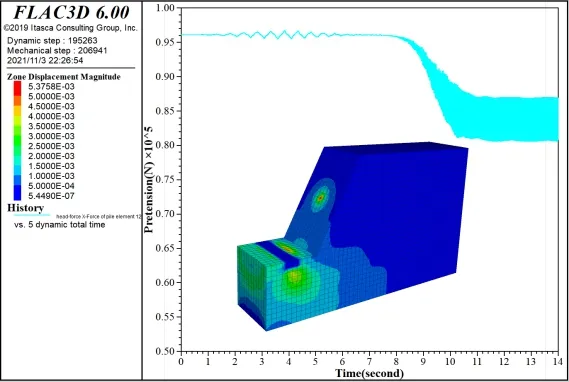
图7 锚头锁固力演化时程曲线和边坡变形云图

3.2 坡体变形演化

由图8 可知，坡脚和坡顶变形在加速度基本波形作用的6 s 时间内发生振荡，振荡波形与加速度波形的特征类似，振幅达到5 mm；在6～8 s内，变形振荡衰减；10 s 后，变形趋于稳定.其中，坡高方向的坡脚变形(红虚线)大于坡顶变形(红实线)；坡宽方向的坡脚变形(蓝虚线)小于坡顶变形(蓝实线)。坡长方向几乎未发生永久变形，坡高和坡宽方向发生永久变形，但永久变形分量最大仅为1 mm.

图8 坡脚和坡顶代表点位移演化时程曲线

3.3 锚固界面剪应力演化

在交通荷载作用下锚杆锚固界面剪应力演化时程曲线如图9 所示.

图9 锚杆锚固界面剪应力演化时程曲线

由图9 可知，在加速度基本波形作用期间(6 s以内)，锚杆不同位置处的锚固界面剪应力均发生了伴随振荡，但振幅不大，且界面剪应力沿杆长大致呈均匀分布，除了锚杆底部单元段剪应力达到36 kPa 外，其余单元段界面剪应力均在22～28 kPa；在加速度波形加载结束后，锚固界面剪应力在4 s(即8～12 s)内发生骤变，剪应力分布区间变为-152～120 kPa，其中负号表示剪应力为锚头至锚杆底部指向；12 s 后，界面剪应力分布趋于稳定.

为了比较锚固界面剪应力沿杆长分布的变化，图10 给出了加速度基本波形作用前、作用中以及作用后3 个阶段的剪应力分布，对应着时程曲线上0、4 和13 s 这3 个时刻.由图10 可以看到，在加速度作用前和作用期间，界面剪应力分布变化很小，近似为均匀分布；加载结束后，界面剪应力分布演化从底部正向最大朝头部呈近似线性降低的趋势，在锚杆沿杆长距离底部5 m 附近发生转向，发展为头部负向最大.界面剪应力的转向，本质上是界面锚-土相对位移方向的变化；由于杆体自身变形相对土体变形较小，锚-土相对位移方向的变化主要是由土体变形决定的，这意味着边坡土体在界面剪应力转向位置处发生相向永久变形.这种相向永久变形表明锚杆由交通荷载施加前的被动承载状态转变为交通荷载施加后的主动承载状态.值得指出的是，本模型所采用的界面剪切刚度较小，即土体变形引起的界面相对位移未达到极限剪切位移，界面剪应力也并未达到极限剪切强度，界面始终处于线弹性承载阶段.

图10 不同时刻的锚固界面剪应力分布

3.4 锚杆轴力演化

加速度波形加载结束后，锚杆杆体内残存弹性波传播，引起附近土体的残余加速度。加速度弹性波在锚杆杆体内传播，引起锚杆在不同位置处均发生不同程度振荡.其中，在锚杆中部振荡最为显著，并向锚杆2 端逐步衰减；其最大振幅接近锁固力的40%，最小振幅约为锁固力的6.5%，见图11.

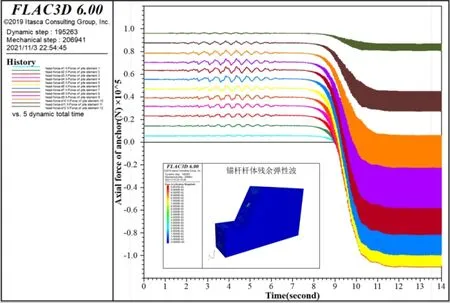
图11 锚杆不同位置处轴力演化时程曲线

4 交通荷载作用位置影响

根据交通选线规划和边坡分级开挖等要求，路面、轨面等交通荷载作用位置可能处于锚固边坡的坡顶或坡脚，从而造成其振动传播路径有所差异.基于所提锚固边坡基准数值模型，将交通荷载作用位置从置于边坡坡脚一侧平面上变化为置于边坡坡顶之上(见图2)，以此来分析锚固边坡服役特性的变化.

4.1 锚头锁固力演化

在2 种不同交通荷载作用位置下，锚杆锚头锁固力的演化曲线如图12 所示.

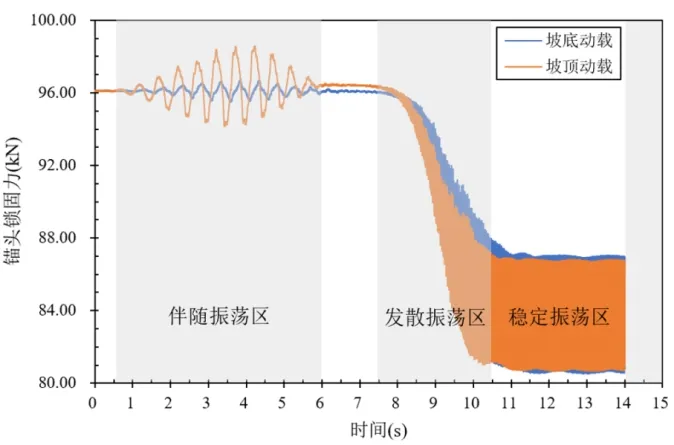
图12 不同交通荷载作用位置的锚头锁固力演化时程曲线

由图12 可发现，无论交通荷载作用在坡底或坡顶，锚头锁固力时程演化均表现为3 个阶段，分别为伴随振荡区、发散振荡区和稳定振荡区，且3 个区域的持续时间基本一致，分别对应0.5～6 s、7.5～10.5 s 和11～14 s；在3 个振荡区之外，还存在0～0.5 s 和6～7 s 这2 个微弱振荡区；相比于交通荷载作用在坡底，坡顶动载作用时的伴随振荡区的振荡幅度提高了100%，发散振荡区的发散幅度有所降低，稳定振荡区的振荡幅度略有减小.

4.2 坡体变形演化

坡顶交通荷载作用引起的锚固边坡特征点变形时程演化如图13 所示.

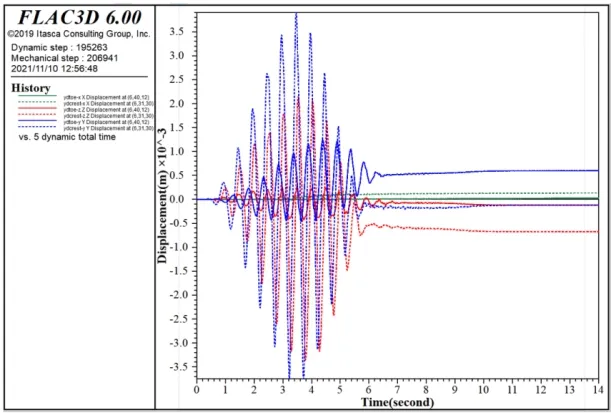
图13 坡顶动载下边坡变形演化时程曲线

与图8 所示的坡脚动载工况对比，可以看出，坡底动载下，边坡坡顶变形主要为y分量，坡底变形主要为z分量；坡顶动载下，边坡坡顶变形主要为z分量，坡底变形主要为y分量.由此说明，交通荷载在作用位置附近主要引起坡体沉降变形，而在作用位置较远区域则主要引起坡体剪切滑移变形.

4.3 锚固界面剪应力演化

坡顶动载下，锚杆锚固界面剪应力演化时程曲线如图14 所示.

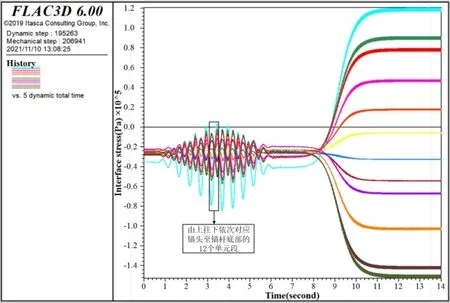
图14 坡顶动载下锚固界面剪应力演化时程曲线

由于锚固界面剪应力是锚杆轴力的一阶微分，其演化特征与锚头锁固力类似.相比坡底动载情形，在锁固力伴随振荡区的时间内，其振荡幅度上升了1 个数量级，最大振荡幅度达80 kPa；但在发散振荡区和稳定振荡区对应的时间内，交通荷载作用位置变化对界面剪应力演化的影响并不显著.值得说明的是，基于本文分析模型，交通荷载无论作用在坡底或坡顶，在锚杆承载全过程中，锚固界面剪应力变化(最大160 kPa)均未超过界面极限剪切强度(175 kPa)，即锚固界面剪切一直处于弹性承载阶段.

5 锚杆空间布局影响

为了评估锚固边坡锚杆在坡体中的设置位置对其动力承载特性的影响，将基准模型中的锚杆位置从坡面中心分别向坡顶和坡底方向移动一定距离，即锚杆倾角不变，锚头沿坡面只在z方向上移或下移6 m，考察3 种不同锚头位置工况的具体影响.需要说明的是，前述分析已发现锚头锁固力作为锚杆端部轴力，其对锚杆不同位置处的轴力具有同步效应(见图11)，锚杆轴力作为锚固界面剪应力的一阶积分，其对锚杆不同位置处的锚固界面剪应力具有同步效应(见图9和图14)，即锚头锁固力时程演化对锚杆轴力和锚固界面剪应力具有强代表性.下面将重点对比分析在锚杆不同设置位置下锚头锁固力和边坡坡体变形响应的演化差异.

5.1 锚头锁固力演化

在坡底交通荷载作用下，锚杆在坡面不同位置工况下锚头锁固力的时程演化曲线如图15 所示.由图15 可知，位于不同坡面位置的锚杆锚头锁固力均具有伴随振荡区、振荡发散区和稳定振荡区的一般特征.然而，相对坡面中心锚杆对应的发散幅度单调递增，坡面下部锚杆和坡面上部锚杆对应的振荡发散区会出现2～3 个波动，且表现为发散过程中锁固力在部分时间段内会超过伴随振荡区的稳定值.这种发散幅度的波动异常主要是锚杆坡面位置的空间非对称性引起的(空间非对称性会导致振动在坡体边界处非对称反射，并在锚杆附近坡体内产生干涉叠加，这种干涉影响在坡底和坡顶附近会被进一步放大).

图15 锚杆在不同位置处的锚头锁固力时程演化

当锚杆在坡面不同位置时，其对应的稳定振荡幅度也有较大差异.其中，坡面中心锚杆的稳定振荡幅度约占伴随振荡区稳定振荡幅度的6.8%；坡面上部和坡面下部锚杆的稳定振荡幅度约占伴随振荡区稳定振荡幅度分别为23.3%和20.6%，且分别是坡面中心锚杆的4 倍和3 倍.上述差异表明，坡底交通荷载振动传播至坡体后，其残余振动主要集中在坡顶和坡底边界附近，且残余振动引起的锚杆锚头锁固力波动幅度较大.为防止多频次交通荷载作用下锚头锁固力大幅稳定振荡造成预应力损失和疲劳破坏，在设计计算时应给予坡脚和坡顶附近锚杆更多的预应力设计冗余.

5.2 坡体变形演化

图16(a)为不同锚固位置的边坡在坡底交通荷载作用下坡脚代表点的变形响应.由图16(a)可以看出，边坡坡脚变形对于锚固位置变化主要表现为朝向坡面外的y位移和竖向的z位移，在边坡宽度x方向上基本没有变形.锚杆设置在坡面中心时，坡脚y位移在伴随振荡段的幅度最大，约为锚杆设置在坡面上部和下部时的3 倍；振荡稳定后的残余坡脚位移也最大，且位移方向朝向坡面内部，而坡面上下部设置锚杆对应的残余位移很小，下部锚杆对应坡脚外移约为0.5 mm.坡脚竖向z位移，对于锚杆设置坡面上部或下部并不敏感，二者演化曲线基本重合，伴随振荡段幅度约为中心锚杆时的3 倍，中心锚杆基本未产生残余沉降，坡面上、下部锚杆则发生约1 mm 的残余沉降.综合来看，在坡底交通荷载作用下，坡面中心锚杆可有效约束坡脚残余外滑和残余沉降，坡面上部锚杆和下部锚杆均可促进坡脚残余隆起.

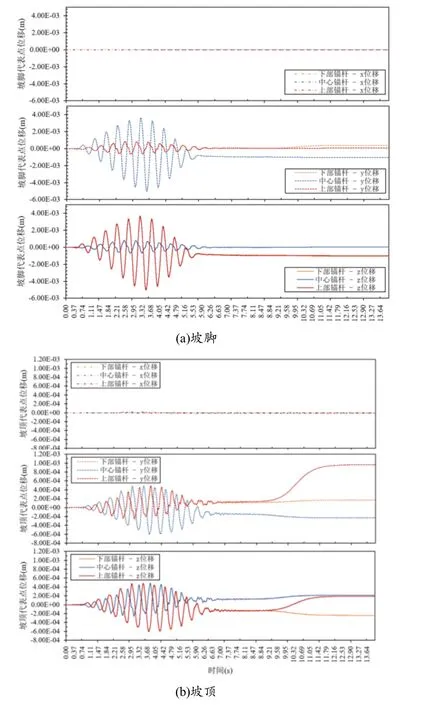
图16 锚杆在不同位置处的边坡位移时程演化

图16(b)为坡底交通荷载作用下锚固边坡坡顶代表点位移分量随作用时间的变化曲线.由图16(b)可知，与坡脚变形类似，无论锚杆设置位置如何，坡顶在坡宽方向上没有发生明显变形，代表点的x位移基本为0.考察坡顶滑动变形，即代表点的y位移，可以发现：当锚杆设置在下部坡面时，坡顶虽在伴随振荡段产生波动外滑动，但仅残余0.15 mm 的外滑量；在坡面上部锚杆情形下，伴随振荡外滑动幅度大于内滑动幅度，残余外滑量在1 mm 附近稳定；在坡面中心锚杆情形下，伴随振荡的外滑和内滑幅度相当，最终稳定在0.3 mm 的内滑量.进一步考察坡顶竖向变形，在中心锚杆情形下，坡顶在伴随振荡段的沉降幅度小于隆起幅度；坡面上部和下部锚杆情形下，坡顶在伴随振荡段的最大沉降幅度超过最大隆起幅度约50%；上部锚杆和中心锚杆对应的残余竖向变形均趋近0.2 mm 隆起，下部锚杆则对应0.3 mm 沉降.综上，在坡底交通荷载作用下，坡面中心锚杆对坡顶外滑和沉降的稳定效果较好，坡面上部锚杆可促进坡顶残余外滑，坡面下部锚杆则可促进坡顶残余沉降.