A novel multi-level model for quasi-brittle cracking analysis with complex microstructure

Xiao-xiao SUN ,Xiang-yu CHEN ,Xiao-ming GUO✉

1Jiangsu Key Laboratory of Engineering Mechanics,Department of Engineering Mechanics,Southeast University,Nanjing 210096,China

2School of Civil Engineering,Southeast University,Nanjing 210096,China

Abstract:The paper presents a novel multi-level model for quasi-brittle cracking analysis.Based on the partition of unity and information transmission technology,it provides a new non-re-meshing way to describe the cracking phenomenon in structures constructed from materials with complex microstructures.In the global model,the concept of the material particle is defined and the basic unknowns are the boundary displacements of these particles,which is different from the concept of the traditional displacement field.A series of enrichment functions with continuous steps is proposed,describing the boundary displacement affected by crack bands and allowing the intersections of crack bands with particle boundaries a priori unknown.Simultaneously,additional equations are introduced to determine element status and make the degrees of freedom of the global model remain at a stable level.Compared with previous research by our group,where the local description is equal to the global description on the boundary of a material particle,the introduced enrichment functions enable more accurate capture of the characteristics of the crack band.The model avoids the complex and dynamic model adjustments due to the activation and exit of representative volume elements(RVEs)and the accuracy of the description of the crack pattern can be ensured.The RVEs are activated at first,but then many of them exit the computation due to the unloading which reduces many of the degrees of freedom.Two examples of concrete specimens are analyzed,and the concrete fracture experiment and the digital image correlation (DIC) test are conducted.Compared with the reference solutions and the experimental data,even though the microstructure of concrete is very complex,the cracking process and crack pattern can be obtained accurately.

Key words:Multi-level model;Concrete;Enrichment function;Quasi-brittle cracking;Damage evolution;Digital image correlation(DIC)test

1 Introduction

The cracking phenomenon in engineering structures consisting of quasi-brittle materials is a multilevel problem.Microstructures and physical properties play a very important role in the initiation and evolution of crack bands.Micro-cracks distributed in components affect the macroscopic properties of the material,resulting in degradation of material stiffness.Their progressive evolution results in the formation of crack bands,which affect the specimen or structure and drive the damage from the material level to the structural level.Well-known examples are the cracking phenomena of structures constructed by concrete,rocks,and other quasi-brittle materials(Hanganu et al.,2002;Wang et al.,2014;Xu et al.,2014;Sun and Li,2016c;Zhang et al.,2019).Many constitutive laws and numerical methods have been developed to simulate these phenomena and satisfactory results have been obtained (Contrafatto and Cuomo,2007;Jirásek and Bauer,2012;Jouan et al.,2014;Li et al.,2015;Abbas et al.,2016).One of the important topics is to understand the nature of failure at the material level and to analyze the process with an advanced model(Wu,2018;Ma and Sun,2020).The other issue is to establish a reliable method for studying damage transscale evolution and its effect on the structure.

For this purpose,many micromechanics methods(Feng and Yu,2010;Dutta and Kishen,2018) and mesoscopic numerical models (Häfner et al.,2006;Wriggers and Moftah,2006;Zhou and Hao,2008;Liu et al.,2009;Shahbeyk et al.,2011;Kim et al.,2013;Rodrigues et al.,2016) have been developed.Because of the exact representation of the complex microstructure,the modeling of the responses at the material level is very accurate.However,the computational effort for conducting mesoscopic analysis is very high.Therefore,many multi-scale or multi-level models are proposed (Guidault et al.,2007;Li et al.,2007;Gitman et al.,2008;Macri and De,2008;Kulkarni et al.,2010;Lloberas-Valls et al.,2011;Ghosh and Chaudhuri,2013;Shen et al.,2014;Nezhad et al.,2016).Of these models,two approaches are the most popular:the hierarchical and concurrent ones.

In the hierarchical approach,a representative volume element(RVE)is defined(Nguyen et al.,2011),and macroscopic material behavior is obtained by using the RVE boundary value problem.This avoids dealing with complicated macroscopic constitutive laws and is successfully applied in nonlinear problems with heterogeneous properties (Dascalu et al.,2010;Coenen et al.,2012).The advantage of the approach is that it saves a large number of degrees of freedom when dealing with the macroscopic problem.Also,when the adaptive methodology is introduced,there are few adjustments of the model needed due to the nature of its information transmission.

The concurrent method usually includes several subdomains in a model to represent the entire structure (Ghosh et al.,2007;Li et al.,2009;Sun and Li,2016a).These subdomains are associated with different scale characteristics.Coarser meshes and macroscopic constitutive laws are employed where the material behavior is linear.For the regions where damage initializes and nonlinear material behavior is anticipated,finer meshes and the physical properties of different components are considered.Using this method,the problems are solved simultaneously.

An adaptive strategy is usually adopted in the concurrent model as well(Sun and Li,2015).It replaces the coarser model with the finer model only in the regions where damage occurs,which reduces the computational cost as much as possible.An attractive advantage of the adaptive concurrent method is that it restores the microscopic characteristics of critical regions completely.So,the damage distribution and the crack path can be obtained with relatively high precision.The method has been applied to structures constructed not only with traditional materials but also with materials with special properties (Chaudhuri,2013;Greco et al.,2015).

In addition to these popular multi-scale methods,some improved or novel models are proposed for damage and crack analysis.Liang et al.(2018) proposed a mesh-size-objective model.By introducing a damage law directly from the micro-cell simulation,where the micro-cell size should be identical to the macroscopic mesh size,the mesh size independent finite element analysis of quasi-brittle material is realized.Some other research (He et al.,2020) has presented a numerical homogenization technology based on the phase-field model for the analysis of fracture of heterogeneous porous media.For damage analysis of rocks,a multi-scale model based on grain-based discrete element method (GB-DEM) (Li et al.,2018)and a simplified multi-scale damage model (Nezhad et al.,2016) have been proposed.For concrete,some researchers have presented a mesh-free meso-macromulti-scale method (Ghosh and Chaudhuri,2013) to analyze its fracture.

In the present paper,a novel multi-level model based on partition of unity (MLPU) is proposed.The information transmission methodology (Berke et al.,2014) is adopted and two separate levels are applied in the simulation.There are very few adjustments to the global model due to the evolution of crack bands and the activation and exit of RVEs.The solutions of RVEs are transferred to the properties and responses of material particles at the global level.This avoids the complex and dynamic model adjustments relating to re-meshing,the variations of physical properties and microscopic structures,the varying trans-level interfaces,and the connection of models from different levels.The information exchange between different levels does not rely on the Gauss point and averaging theory.It reduces the assumption relating to the RVE boundary conditions and allows the arbitrary crack band pattern theoretically.Simultaneously,as in the classical concurrent method,the critical regions are actually controlled by finer characteristics completely,which ensures precision.

The concept of the material particle is defined,and the basic unknowns at the global level are the boundary displacements of these particles.A series of enrichment functions with continuous steps is developed,and the partition of unity method is adopted to approximate the boundary displacement.That method avoids the consideration of the global internal displacement field of the particles.The equivalent description of crack bands in the global model is simplified because there is no need to consider the location,length,and direction when inserting a specific displacement mode that describes cracking.The additional equations are introduced to determine element status,making the degrees of freedom of the global model remain at a stable low level all the time.Simultaneously,the exit of RVEs reduces the number of degrees of freedom and keeps the degrees of freedom of the entire model at a low level during the analysis.This is a totally non-re-meshing framework.It is suitable for specimens or structures constructed by engineering materials with complex microscopic structures.Numerical results of concrete specimens are obtained and the fracture experiment and digital image correlation(DIC) test are conducted.It shows that the crack path can be captured accurately even though its pattern is intricate.

2 Numerical model of global level

2.1 Description of the global problem

In this section,the global governing equations adopted in MLPU are established,with the basic unknowns defined on the boundaries of material particles.

For a boundary value problem,the classical equation gives

whereσis the stress tensor andbthe body force.∇is the derivative operator.The essential and natural boundary conditions should be satisfied on corresponding boundaries of the entire solving domainΩas well.Herein the damage evolution and cracking behavior are focused on and,for convenience,the body force will not be considered.Therefore,the equivalent weak form reads:

where δuand δεare the test function and its gradient,respectively;denotes the surface tractions on ∂Ωσ,∂Ωσ∪∂Ωu=∂Ω,and ∂Ωσ∩∂Ωu=∅.∂Ωσand ∂Ωuare the parts of boundary ∂Ω,which are imposed with tractions and displacement,respectively.Γrepresents the area of the boundary.Here,a particle concerning a domain will be defined.The particle possesses a limited size and both its deformation and cracking properties are determined by itself.To this end,Eq.(2)is expressed as the following discrete sum:

whereNdis the number of particles in the entire solving domain.Then,the Gauss divergence theory is applied to obtain the weak form expressed with tractions.That is,findu[l](l=1,2,…,Nd)such that

withΩland ∂Ωlas the domain and its boundary associated with thelth particle,respectively.Eq.(4) is equivalent to Eq.(3) andTis the operator reflecting the intrinsic deformation and cracking properties of each particle.These particles are referred to as material particles hereafter.One should note that adjacent material particles share the same displacement on the common boundary.It is obvious that the tractionst[l]on the boundary of thelth material particle are determined by the boundary displacementu[l].

Eq.(4) is taken as the governing equation of the global problem here,together with essential boundary conditionsu=,whereis the displacement employed on ∂Ωu.It can be seen that the boundary tractionst[l]can be obtained ifu[l]is given,whether the material particle is undergoing distributed damage evolution or cracking.It avoids the representation of the internal status of a material particle at this level.The material particle is intact at the beginning.It may undergo distributed damage evolution and eventually it may crack.It is complex to consider when and where an accurate displacement mode should be embedded to describe the cracking phenomenon,which relates to a consideration of location,length,and direction of possible crack bands.Therefore,using Eq.(4) to deal with the same problem,the displacement modes associated with crack bands are embedded only on the boundaries of material particles,which significantly simplifies the problem.

2.2 Discrete governing equations

Given the exact operatorT,the basic unknowns of the global problem,namely,u[l](l=1,2,…,Nd) are to be obtained precisely if they are approximated reasonably.First,the boundaries of material particles are discrete as depicted in Fig.1.

Fig.1 Discretization of material particles’boundaries.The variables are explained in the text

The regions with high deformation gradient related to crack bands are assigned enriched elements while the remaining regions are assigned normal elements.One should note that the enrichment is implemented on the boundaries of material particles but not implemented inside them.The resulting approximation of boundary displacement states

It should be noted that the enriched shape function and the shifted enrichment function both correspond to two indices,jandq.The enriched shape function is rewritten as

and the shifted enrichment function is denoted as

The effective coordinate is a scalar because it locates a point on the particle boundary.For simplification,the shifted enrichment function will be referred to here as the enrichment function.

The displacement depends not only on the normal and enriched degrees of freedom but also on the status of each element,namely,if the element is currently enriched or not.Letdbe the vector denoting all the degrees of freedom andχthe variable representing the status of all elements.It shows thatu=φ(d,χ),whereφis the mapping from degrees of freedom and element status to the displacement.Here,d,χ,anduare variables for the entire global model.These variables for each material particle are denoted byd[l],χ[l],andu[l],respectively.d(k),χ(k),andu(k) are variables for each element.Therefore,the discrete form of Eq.(4) can be obtained:

as the nodal forces of elementkobtained from the material particlel,and

as the external nodal forces employed on elementkσ.Sldenotes the element set including all elements on the boundary of material particlel.denotes the region assigned with elementkon ∂ΩM,andrepresents the region assigned with elementkσon ∂Ωσ.δd(k) andare virtual displacements of the corresponding degrees of freedom.Here,

N0，(k)andare matrices of shape functions and enriched shape functions associated with elementk,respectively.Tractionst[l],(k)(d[l],χ[l])in Eq.(10)represent tractions of material particlelonwhich are determined byd[l]andχ[l].Introducing the mappingΨthat determines element status from boundary deformation of all material particles,an equation is added to find the additional variableχ,as depicted in Eq.(9).

Simplifying Eq.(9),it can be expressed as

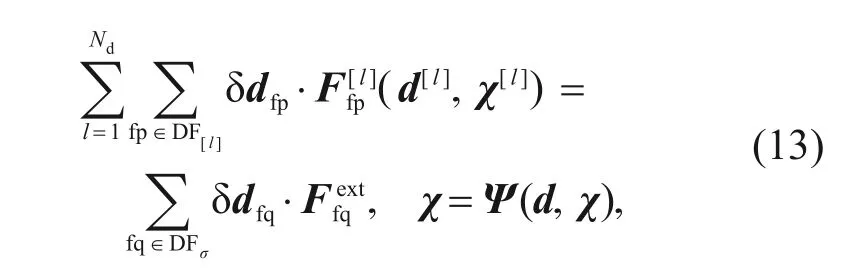
The additional equation in Eq.(13) means that,if there is a solution of boundary displacement which is accurate enough,a proper rule or mapping can be introduced to determine where enrichment should take place according to the deformation.So,introducing the enrichment only on these regions will obtain a solution that is accurate enough.Letχbe the element status determined by the solution that is accurate enough then,using this element status to solve the displacement,the obtained solutionsdandχwill be accurate enough because the proper element status is used.So,the element status determined by the solution that is accurate enough can be obtained,namely,Ψ(d,χ),which should be equal toχ.

It is obvious that the deformation of boundaries of the material particles determines if the element should be enriched.Here the right side of the added equation in Eq.(13)is detailed.

2.3 Enrichment functions

Here we treat the cracking phenomenon as the evolution of localized damage or crack bands in a structure,a viewpoint that is usually applied in quasi-brittle fracture analysis.The crack bands will intersect with the boundaries of material particles.To capture the characteristic of a high deformation gradient,a set of enrichment functions with continuous steps locating on specific gaps is proposed.The jump herein will be described in a continuous manner.Different from the classical step function,the proposed enrichment functions describe a jump using displacement difference accumulated on specific gaps,which can reflect severe local deformation when some of the corresponding coefficients are significant.They also allow the intersections of crack bands with boundaries of material particles a priori unknown.

As shown in Fig.2,the particle boundaries affected by crack bands will be subjected to inserted enrichment functions.The enrichment functions have a specific influence region associated with the crack zone.A series of enrichment functions with different continuous steps is set one by one.The influence region will be covered by these continuous steps.Actually,the definition of enrichment functions does not depend on the distribution of elements.For the convenience of implementation,given the gap sizedgap,the number of gaps in the element can be set as an integer:

Fig.2 Description of enrichment functions on the boundary of a material particle

where(·)pand(·)qdenote the effective coordinates of element nodes.The gap is used for capturing local high deformation gradient.Thus,the gap size should be notably smaller than the element size,because the element serves as the global description.

The enrichment functions in the element are shown in Fig.3.As in the adoption of shifting,the blend elements are eliminated.A series of reference points is defined for description,as depicted in Fig.1.These reference points are denoted asand the gaps are represented byActually,there are no degrees of freedom on reference points,and they are just used for reference purposes.

Fig.3 Enrichment functions in the element

The enrichment functions give:

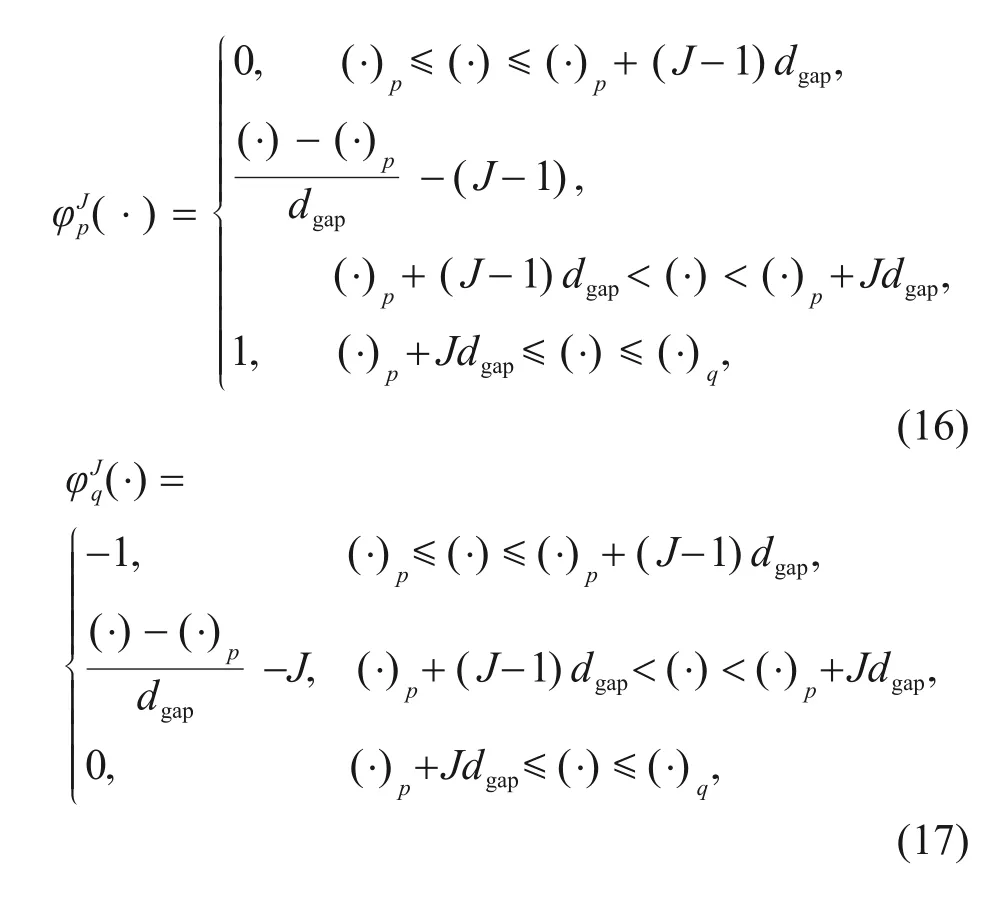
withJ=1,2,…,Ngapthe local number of enrichment functions.The local numberJcorresponds to the position of the continuous step.

It is obvious that the size of one or several gaps can make up the width of the intersection of the crack band with the particle boundary if the size of each gap is reasonably small.The coefficients of enrichments,which are associated with the amplitudes of continuous steps,indicate severe local deformation.

The features of these enrichment functions make it possible to capture the intersections of crack bands with elements automatically and remove the need to know the positions of the intersections beforehand.The element will be enriched if a high deformation gradient is approaching.If there is no crack,the enriched degrees of freedom play the role of representing local deformation relating to finer characteristics.Otherwise,some of the enriched degrees of freedom describe severe local deformation caused by cracking,with the corresponding continuous steps being manifest somewhere.No strict distinction between continuous and discontinuous regions is required,and the displacement modes associated with cracking are available anywhere.With the combination of these enrichment functions,the cracking of particle boundaries will be captured automatically.

Enriched shape functions are depicted in Fig.4.It should be noted that,at the ends of the element,where the gap 1 and gapNgapare located,the values of enriched shape functionsare zero at all the four endpoints of gap 1 and gapNgap.The specific locations make the features of enrichment functionschange significantly after they are multiplied by corresponding shape functions and result in a loss of ability to represent cracking and results in the singular matrix.Simultaneously,it is easy to see that the enriched shape functionsandare the ones that can represent cracking independently at corresponding positions.Therefore,are deleted.

Fig.4 Enriched shape functions of the element

The mesh of the global model remains unchanged during analysis.It avoids re-meshing which leads to large adjustments to global model information.Combined with the solution of element status,the enrichment can be implemented at the most necessary positions.

3 Multi-level computational framework

The operatorTis usually complicated due to the underlying characteristics of quasi-brittle materials.It brings difficulty in dealing with the governing equations.The initiation and evolution of crack bands strongly relate to the microstructure as well.Therefore,the microstructure is introduced,and a multilevel computational framework is established.

To this end,an RVE is assigned to the material particle,replacing the functions of the operatorT.The stiffness matrix and domain forces of the material particle are obtained by conducting the RVE problems.The implementation contains two steps.First,the boundary displacement of the material particle is transmitted to a finer level.It is applied on the boundary of RVE,as depicted in Fig.5.

Fig.5 Multi-level information transmission model

The displacement of the mesoscopic node np gives

with np the number of the mesoscopic node on the boundary of RVE.mkis the set containing the mesoscopic nodes covered by the location of elementk.The RVE problem is then solved,and the responses and reduced stiffness matrixof RVE are obtained (Kouznetsova et al.,2001;Biswas et al.,2019).

Then the domain forces and domain tangent stiffness matrix of the material particle are obtained,as follows.Using reaction forces of mesoscopic nodes on the boundary of RVE,domain forces in Eq.(13)can be simplified into a discrete sum:

and considering Eqs.(21) and (22),the variations of domain forces are

and the resulting domain tangent stiffness matrix is obtained:

The domain forces and domain tangent stiffness matrices are to be assembled for solving global problems.

For intact material particles with linear properties,or the material particles the RVEs of which have exited the computation,the process is unnecessary.The initial,or current,domain stiffness matrices are employed to obtain domain forces directly.

Here,a damage criterion is introduced according to the deformation of the material particle.It determines if the material particle is undergoing damage evolution and relates to the activation and exit of RVE.It gives:

where(d[l]，χ[l]) is the deformation characteristic variable which describes theξth type of deformation degree of material particlel(ξ=1,2,…,η);ηis the number of deformation characteristic variables attached to a material particle andEξ,cdis the critical value of each type of deformation characteristic variable.

If any critical value is reached,it means that damage could occur somewhere in the material particle and the corresponding RVE will be activated.Simultaneously,some material particles undergo damage first,and then the damage evolutions stop due to unloading.There is no need to analyze the damage evolutions for such material particles in the following computational process.The corresponding RVEs will exit computation to save computational cost according to the damage criterion as well.Although the damage criteria for the activation and exit of RVE could be different,for simplification,the same criteria are adopted.This is a conservative approach and ensures accuracy.For the material particles the RVEs of which exit the computation,the domain stiffness matrices will be obtained from the moments when exit occurs.For the unloaded material particles,these stiffness matrices remain unchanged in the following,and the domain forces will be obtained directly using these domain stiffness matrices.The implementation is very easy.The RVEs just exit computation directly,and no adjustment for the global model needs to be dealt with.For our analysis,the local unloading due to the formation of the crack band is mainly focused upon.It usually results in the unloading of the regions on two sides of it.Considering this situation,there may not be a very apparent compressive load to make the microscopic crack surfaces subject to compressive forces.The monotonic loading process is considered here.

Here the deformation characteristic variables of element and material particle are detailed.Both the deformation characteristic variables,corresponding to material particles and elements,describe the deformation that can cause damage or a crack.Many deformation characteristic variables can be defined for different materials and analysis demands.Here,the tensile deformation degree of the element is defined to establish the criterion.Considering that the quasi-brittle materials employed in engineering structures are usually sensitive to tensile deformation,and the two different directions of elements on the boundaries of material particles can help to detect tensile deformation from many different directions,the deformation characteristic variable is suitable for many cases of cracking analysis if a proper critical value is set.Further study of the definition of these deformation characteristic variables will be the subject of future work.

For the elements,the deformation characteristic variable is defined as

anddenote the sizes of elementkbefore and after deformation,respectively.represent the sizes of gaprJbefore and after deformation,respectively.For the current normal element,if(d，χ) reaches the critical valueE1,ce,it will become an enriched element.Conversely,an enriched element will revert to a normal element if the maximum tensile deformation of gaps is lower than the critical value,which indicates that the corresponding region is unloaded and the enriched degrees of freedom are unnecessary.It usually occurs for the following reasons.The intact region with the possibility of damage,because it has undergone relatively high stress,is now unloaded or the region with microcracks is now unloaded,and the micro-cracks are now almost closed.That ensures that the degrees of freedom of the global model keep at a stable low level.

For material particles,the deformation characteristic variable is defined as

withε[l]t，maxbeing the maximum tensile deformation degree among the elements on the boundary of material particlel,which gives

The high tensile deformation degree appearing on the boundary could cause damage not only near the boundary but also inside the material particle.The critical values of the deformation characteristic variables associated with the elements and with the material particles can be different.For simplification,the two critical values are set here to be equal.So,the exit of RVE requires all the boundary elements of a material particle to return to the normal ones.The implementation of MLPU is given in the electronic supplementary materials,including the solution steps of the multi-level model.

4 Results and discussion

To demonstrate the effectiveness of the proposed multi-level model,the cracking processes of a concrete beam and an L-shaped concrete specimen are analyzed.The results are compared with experimental data and reference solutions obtained from the full microscopic model.

4.1 Bending test of beam specimen

In Fig.6,the geometry and boundary conditions of a concrete beam specimen with an out-of-plane thickness of 150 mm are shown.The displacement load is applied on the top of the simply supported beam.About 150 loading steps are used when analyzing the bending test.The RVE of the MLPU is shown in Fig.6b.The full microscopic model is shown in Fig.6c.The RVE is constructed from lattice elements,and the element parameters are determined according to Guo et al.(2009).The complex microstructure of concrete is represented by the existence of aggregates,matrix,and the aggregate-matrix interface zone (ITZ).The Monte-Carlo method (Zhang et al.,2012;Sun et al.,2020)is employed to generate the distribution of polygonal aggregates.As the scale of RVE is significantly larger than the maximum microscopic characteristic scale (usually the diameter of the biggest aggregate),the RVE can represent concrete material and the specimen can be viewed as constructed by this microscopic structure repeatedly.Actually,the RVE can be constructed by many kinds of numerical models because there is no restriction of model type as long as the information transmission process can be implemented.

Fig.6 Bending test of beam specimen:(a) geometry and boundary conditions;(b) RVE of MLPU model;(c) full microscopic model.F:reaction force;u:displacement

The well-known Mazars’ damage model (Sun and Li,2015)is adopted to describe the deterioration of components of concrete and the damage variable gives

whereεis the tensile strain andεptis the strain threshold of damage,which can be determined by the tensile strength of the materials.AtandBtare damage parameters.Considering the randomness at the finer level and the essence of tensile failure at the microscopic level,tensile damage is considered.The elastic modulus and Poisson’s ratio of the aggregate,matrix,and ITZ areEagg=45.0 GPa,Em=30.0 GPa,Eitz=22.5 GPa,andvagg=vm=vitz=0.2.The failure of aggregate is not considered,and the tensile strengths of matrix and ITZ areft,m=5.0 MPa andft,itz=2.81 MPa.Damage parameters areAt=0.84 andBt=22900.The critical value of the deformation characteristic variable of the material particle isE1,cd=6.7×10-5.

Fig.7 shows the specimen deformation at the end of the analysis(with a scaling factor of 50).The deformation of enriched elements 1,2,and 3 in Fig.7a reflects the main crack path,illustrating the locations where the crack band crosses the boundaries of material particles,which is consistent with the reference model (full microscopic model) in Fig.7b.Elements 4 and 5 are enriched because the damage occurs in the regions and the unloading is not sufficient.By comparing with the crack pattern in microstructure detailed in Fig.7b,although the microstructure is complex,the variation of the crack path can be captured.

Fig.7 Deformation of beam specimen:(a)MLPU;(b)full microscopic model

The damage evolution process obtained from MLPU is shown in Fig.8,together with the variation of element status and the exit of RVEs.Enriched elements are the red ones in the global model and the damage status of activated RVEs is depicted on the right.To show the damage pattern clearly,the microstructure is not displayed here.It can be seen that damage is distributed near the bottom of the specimen at first,and only three RVEs are activated.Gradually,the crack band forms and propagates toward the top of the specimen.The RVEs are activated successively to adapt to the damage evolution.There is no re-meshing and model replacement operation,and RVEs are not inserted in the global model.The change to element status usually only happens when the front end of the crack band approaches or leaves the boundaries of material particles.Thus,the change is not frequent.With the propagation of crack band and with unloading occurring on both sides of it,many enriched elements in the unloading region turn to normal ones,which makes the degrees of freedom of the global model keep at a stable low level.Simultaneously,the damage evolution stops in the unloaded RVEs.They exit the computation and the current material properties are reserved in corresponding material particles,which reduces a large number of degrees of freedom and improves the efficiency.

Fig.8 Damage evolution process,variation of element status,and RVE exit of beam model obtained by MLPU:(a)60%umax;(b)64%umax;(c)68%umax;(d)72%umax;(e)80%umax;(f)100%umax.umax is the failure displacement employed on the specimen

The load versus displacement curves and the damage distribution of failure specimen are compared with reference solutions,as shown in Figs.9 and 10.Simulation results obtained by MLPU are consistent with the reference model.A relatively large element size is adopted in the global model to obtain a coarse solution,which results in a difference of the linear part in Fig.9a under this specific boundary condition.

As shown in Fig.9b,the simulation results of the MLPU model with RVE exit are compared with the model in which the exit of RVE is not considered.Almost the same results are obtained,demonstrating that the damage in unloaded regions will not continue to develop and that RVE analysis in these regions is not necessary.The degrees of freedom and the number of elements for MLPU and reference solution are compared in Fig.11a.A comparison of the two MLPU models is depicted in Fig.11b.During analysis,the degrees of freedom of MLPU increase first and then decrease due to the exit of RVEs.RVE analysis is only activated in the most necessary regions and so the degrees of freedom of the entire model are kept at a stable low level all the time.Simultaneously,there is no re-meshing,model replacement,or re-computation.The activation and exit of RVE are easy to implement.

Fig.9 Load versus displacement curves for beam model:(a) MLPU and the reference solution;(b) MLPU with RVE exit and without RVE exit

Fig.10 Damage distributions of failure beam specimen:(a) reference solution;(b) MLPU,gap size 2 mm;(c) MLPU,gap size 2.5 mm;(d) MLPU,gap size 3.3 mm.Inactivated RVEs in (b-d) are added to paint the entire specimen for comparison

Fig.11 Number of active degrees of freedom (DOFs) and elements in beam specimen during analysis:(a) MLPU and reference solution;(b)MLPU with RVE exit and without RVE exit

Here the mesh size dependency is discussed.First,it should be noted that the proposed method is different from the homogenization method.Therefore,the concept of mesh size dependency is different.

For a multi-level framework,the size dependency of the global model is an important problem.Therefore,given the reference model (full microscopic model),the size dependency of the global model is focused on here.There may be some size dependency in the microscopic model due to the adoption of Mazars’constitutive law.However,as a classical constitutive law,it is still adopted by some microscopic models to simulate the quasi-brittle cracking phenomenon(Sun and Li,2015,2016a,2016b).

For the proposed method,three parameters are possible factors relating to the size dependency.The size of the material particle will be discussed first.It resembles the size of the macroscopic element in the homogenization method.However,the meanings relating to size dependency are very different.For the proposed method,no averaging theory is adopted,and the information transmission does not rely on the Gauss point of the macroscopic element.The size of the material particle is equal to the corresponding RVE.Actually,the material particle is an object which is accurately equivalent to the region with microscopic features (RVE).In this respect,it is similar to the concurrent method,and the size of the material particle is not related to size dependency,as shown in Fig.12.Similarly,the mid-span region with a size of 150 mm×150 mm in the reference model can be regarded as an equivalent object of a big material particle.Compared with the results obtained from the MLPU model in which the size of a material particle is 50 mm×50 mm,it demonstrates that the size of the material particle does not bring size dependency.

Fig.12 Discussion of the size dependency of the material particle:(a) full microscopic model;(b) MLPU with the large size of material particles;(c)MLPU with the small size of material particles

Secondly,the size of the element on the boundary of the material particle is focused on.The element serves as the global description.Usually,the size of the element is relatively large,and the crack bands are narrow regions.The description of displacement in the intersection (the intersection of the crack band with the particle boundary) mainly depends on enrichment functions and not on the size of the element.Therefore,the size of the element does not relate to the size dependency.

The gap size relates to the minimum unit that constructs the width of the intersection (the intersection of the crack band with the particle boundary).It is the size relating to the description of displacement within the crack zone.For discussion of the effect of gap size on simulation results,three different gap sizes are employed.From the curves (Fig.9) and damage distribution (Fig.10),the results are not sensitive to gap size.The reason for that is that the gap can be viewed as a line segment on the particle boundary and it neither stores energy nor can be given any material properties.The phenomenon that the energy dissipation decreases as the traditional element size shrinks will be relieved here.Simultaneously,no material region is enclosed in a single gap (compared to some situations where material is enclosed in the traditional element,and the material deformation depends on the element itself).Note that for the material deformation associated with the crack band near a particle boundary,in each small region on one side of the particle boundary the deformation is controlled not only by the nearest gap but also by a set of gaps nearby.This can bring some interactions and help relieve the size dependency.

In order to verify the effectiveness of the proposed model,a fracture experiment with the concrete specimen is carried out and the crack patterns obtained from simulation and experiment are compared.Fig.13 shows the experimental device and the specimen.The span of the specimen is 450 mm,and the other two sizes are both 150 mm.The grade of concrete is C30.This is a three-point-bending specimen and a displacement load is applied.The fracture pattern and microstructure of the concrete are shown in Fig.14.The interfacial fracture(left mark)is obvious.Also,there is a phenomenon of the fracture of aggregate on the specimen (right mark).The experimental phenomenon is real and complex.For simulation,some factors are simplified and fracture of the aggregate is not considered.

Fig.13 Experimental device of DIC test

Fig.14 Microstructure and fracture pattern of the concrete

DIC technology is adopted to track the evolution of the crack band.It captures the deformation on the surface of the specimen and then the strain is calculated.Using these data,the crack band can be described.The crack patterns are shown in Fig.15,whereupis the displacement load proportion compared to failure displacement.For the DIC test,the tensile strainεx,which is along the long axis direction of specimen,is used to reflect the crack band.The numerical results are consistent with the experiment results.

Fig.15 Comparison of crack patterns in numerical results(a)and in experiment(b)

4.2 L-shaped specimen

This example shows the results of damage evolution in the L-shaped specimen obtained by MLPU and the reference model.The L-shaped specimen with the same thickness as the beam specimen is analyzed and the geometry and boundary conditions are depicted in Fig.16.The right edge is fixed and the horizontal load is applied on the top of the specimen.About 230 loading steps are used when analyzing the L-shaped specimen.The same RVE and material parameters of the beam model are employed.

Fig.16 L-shaped specimen:(a) geometry and boundary conditions;(b)full microscopic model

The deformation of the specimen is depicted in Fig.17 (with a scaling factor of 50),showing that the results obtained by MLPU are consistent with the reference solution.The crack path can be found following the enriched elements.The crack band initiates at the corner of the L-shaped specimen and passes through several material particles.It shows that there is no restriction of cracking deformation modes of the material particles.The crack band can get into and get out of the material particle from any location,which captures the real crack path.

Fig.17 Deformation of L-shaped specimen:(a) MLPU;(b)reference solution

The damage evolution process,variation of element status,and the exit of RVEs are shown in Fig.18.Distributed damage is first located at the corner.Then,the crack band occurs as in Figs.18b and 18c.The RVEs are activated first and some of them exit the computation due to unloading.Distributed damage usually affects the macroscopic properties of the material but,when it develops to be the crack band,the damage will reach the level of the specimen or structure.The examples of the beam and Lshaped specimen show that the proposed MLPU model is effective in analyzing the damage transscale evolution problem.

Fig.18 Damage evolution process,variation of element status,and RVE exit of L-shaped specimen obtained by MLPU:(a)45%umax;(b)50%umax;(c)55%umax;(d)73%umax;(e)87%umax;(f)100%umax

Figs.19 and 20 depict the load versus displacement curves and damage distribution at the end of the analysis.The results obtained by MLPU are in agreement with the reference solution and the oscillation in the post-peak regime is mainly related to the complex microstructure of concrete.It can be seen that,polygonal aggregates with many corners are used,which are different from the smooth round aggregates.Also,it can be noted that the aggregate fraction is sufficient and the distance between aggregates is relatively small.It makes the microstructure correspond more closely to real material,but it brings more randomness and sensitivity to the numerical model.For example,the stress concentration on the corner of the aggregate will be sensitive to the near environment.Although the enrichment functions improve the accuracy of description on the boundary,it is still an approximation,which does not totally correspond to the reference model.Some difference may therefore occur.Three gap sizes are employed to analyze the problem and consistent results are obtained.The results from the model with RVE exit and model without RVE exit are also compared,which shows that the accuracy is not affected.

Fig.19 Load versus displacement curves for L-shaped model:(a)MLPU and reference solution;(b)MLPU with RVE exit and without RVE exit

Fig.20 Damage distributions of L-shaped specimen: (a) reference model; (b) MLPU, gap size 2 mm; (c) MLPU, gap size 2.5 mm;(d)MLPU,gap size 3.3 mm.Inactivated RVEs in(b-d)are added to paint the entire specimen for comparison

Fig.21 depicts the degrees of freedom and the number of elements during analysis.The degrees of freedom in the MLPU model are obviously lower than those in the reference model,and they can keep a stable low level due to the exit of RVE.

Fig.21 Number of active degrees of freedom and elements in L-shaped specimen during analysis:(a)MLPU and reference solution;(b)MLPU with RVE exit and without RVE exit

5 Conclusions

This paper presents a novel multi-level computational framework for quasi-brittle cracking analysis.It can deal with a damage trans-scale evolution problem which involves the initiation of distributed damage and the formation and progressive propagation of a crack band in the structure.Based on the partition of unity and on information transmission technology,it provides a non-re-meshing way to describe the cracking phenomenon in structures constructed from materials with complex microstructures.

The concept of the material particle is defined on the global level and the basic unknowns are the boundary displacements of these particles.The model avoids consideration of the global internal displacement field of the particles.The equivalent description of crack bands in the global model is simplified because there is no need to consider the location,length,and direction when inserting a specific displacement mode that describes cracking.A series of enrichment functions with continuous steps is developed,describing the boundary displacement affected by crack bands,allowing the intersections of crack bands with particle boundaries a priori unknown in the global model.Simultaneously,additional equations are introduced to determine element status.The normal elements can be enriched due to the approach of crack bands.Also,the enriched degrees of freedom can be deleted in the local unloaded regions.It makes the number of degrees of freedom of the global model remain at a stable status,and the number will not keep increasing during analysis.Compared to previous research reported by our group (Sun and Guo,2019),where the local description is equal to the global description on the boundary of the material particle,the introduced enrichment functions enable the characteristics of the crack band to be captured more accurately.The solutions of RVEs are transferred to the properties and responses of material particles at the global level.Comparing to some existing concurrent methods,it avoids the complex and dynamic model adjustments relating to re-meshing,the variations of physical properties and microscopic structures,the varying translevel interfaces,and the connection of models from different levels.With the damage evolution,the RVEs will be activated at first,and then many of them exit the computation due to unloading.It reduces a large number of degrees of freedom and keeps the degrees of freedom of the entire model at a stable low level throughout.Also,different from some homogenization methods,the information transmission does not rely on the Gauss point in the macro-scale model.It reduces the assumption relating to the RVE boundary conditions and allows the arbitrary crack band pattern theoretically.

Two examples of concrete specimens are analyzed,and the results obtained from the proposed method are compared to reference solutions.The simulation results show that,although the microstructure of concrete is very complex,the cracking process and crack pattern can be obtained accurately compared to the full microscopic model.This is a multi-level model.On the global level,the scale relating to the overall performance of material is considered.For the RVEs,the micro-scale of components is applied.Strictly,the scale separation is not perfect because the scale at the global level is not significantly larger than that at the finer level.However,the scale at the global level is obviously larger than the scale that is suitable for describing the microstructure characteristics of the concrete.Near the main crack band,the unloaded REVs exit the computation and the enriched degrees of freedom are deleted from the unloaded global elements gradually,reducing the degrees of freedom significantly.The degrees of freedom remain stable at a low level during the analysis.For verifying the effectiveness of the proposed model,a fracture experiment on the concrete specimen is conducted.The DIC test collects the strain data and describes the cracking process.The numerical results are consistent with the experimental evidence.It seems that the macro-crack bifurcation phenomenon can be simulated by the proposed framework.For the enrichment functions,it could be modified,for example,using a nonlinear function to describe continuous steps to approach the crack behavior more accurately in the future.

Acknowledgments

This work is supported by the National Natural Science Foundation of China(No.51878154).

Author contributions

Xiao-ming GUO designed the research.Xiao-xiao SUN designed the research and completed the main research work and the paper.Xiang-yu CHEN completed the reference model.

Conflict of interest

Xiao-xiao SUN,Xiang-yu CHEN,and Xiao-ming GUO declare that they have no conflict of interest.