Computational fluid dynamics analysis on flow-induced vibration of a cryogenic poppet valve in consideration of cavitation effect

Ai-bo WEI ,Rong GAO ,Wei ZHANG ,Shun-hao WANG ,Rui ZHOU ,Xiao-bin ZHANG✉

1Institute of Refrigeration and Cryogenics,Zhejiang University,Hangzhou 310027,China

2China Aerodynamics Research and Development Center,Mianyang 621000,China

Abstract:Poppet valves are basic components of many manufacturing operations and industrial processes.The valve plug will withstand unbalanced pressure during the switching process due to the complex fluid-structure interaction (FSI) in the local flow condition,especially with the occurrence of cavitation,which results in a convoluted generation and propagation of mechanical and fluid-dynamic vibrations.In the present work,computational fluid dynamics(CFD)approaches are proposed to model the flow-driven movement of the disc,in consideration of the valve stem rigidity,for a cryogenic poppet valve with liquid nitrogen as the working fluid.Cavitation effects are included in the CFD simulations.The relationship between the displacement of the disc and the resistance of the stem is obtained in advance using the finite element method (FEM),and implemented in CFD calculations based on the user-defined functions(UDFs).The disc vibration is realized using the dynamic mesh technology according to the resultant flow field force and resistance of the stem determined in the UDF.The vibration characteristics of the valve disc,including velocity and vibration frequency,are presented.The temporal evolutions of cavitation behavior due to the vibration are also captured.Comparisons of results between cavitation and non-cavitation conditions are made,and spectral analysis of the transient pressure fluctuations reveals that the presence of cavitation induces transient unbalanced loads on the valve disc and generates instantaneous tremendous pressure fluctuations in the flow field.Various pressure differences between the inlet and outlet as well as valve openings are modeled to probe the influences of FSI on valve disc vibration mechanisms.The consequent analysis gives deeper insights and improves understanding of the mechanism of the complicated interaction between the cavitating flow and the vibration of the valve disc.

Key words:Poppet valve;Computational fluid dynamics (CFD);Cavitation;Flow-induced Vibration;Fluid-structure interaction(FSI)

1 Introduction

Cryogenic poppet-type control valves have always been recognized as being among the most crucial control equipment that is widely utilized in automatic control systems in such as air separation,chemical engineering,and aerospace industries.The function of such valves is to manage flow rate by adjusting the flow area available to the fluid in the action of modulation.An observed phenomenon within the cryogenic control valves is that a vibration of the valve disc occurs under certain operating conditions especially when the pressure differences between the valve inlet and outlet are relatively large.The vibration of the valve disc,which is excited by the unbalanced flow force imposed on the valve disc or by the interaction between the shock-wave and boundary-layer (Duan et al.,2019)as the fluid passes through the valve,may give rise to severe accidents.The stimulation of the poppet’s vibrations is especially intense when the excitation frequencies are close to the poppet’s natural frequencies.Such events can also be accompanied by cavitation,resonance,and even system vibration resulting in calamitous failure (Ahuja and Hosangadi,2006).Therefore,the demand has arisen to analyze the fluid-structure interaction (FSI) characteristics inside the valve,together with the incurred vibration due to the unsteady flows passing through it.

There has been considerable interest in studying the flow-induced vibration (FIV) of valves.Kolkman(1977) proposed a remarkable theory to describe the vibration of the gate valve,indicating that the valve motion introduces hydraulic forces on it,and also summarized various types of hydraulic forces during valve motion.Later,Nakano et al.(1988) studied the mechanical vibration in a pressure-reducing valve under high-pressure reduction.Various types of flow regimes as well as assorted seat and plug geometries were studied and the level of flow instability was found to depend upon the flow structure in the close environs of the plug.Yonezawa et al.(2012) conducted experimental and numerical investigations on a steam control valve FIV to further elucidate the mechanisms of valve disc vibration resulting from unsteady flows around it.Dynamic fluid forces were measured by actuating the valve disc with an exciter and the pressure fluctuations were found to be periodic with the same frequency as the valve disc vibration.Stosiak (2015)carried out experiments and theoretical analysis to study ways of reducing the impact of mechanical vibrations on hydraulic valves and found that introducing shock damping washers,or mounting the distribution valve on flexible washers,was effective.Vedova et al.(2017) proposed a hybrid computational fluid dynamics (CFD)/MATLAB-Simulink approach to determine the pressure field inside the valve and the forces acting on it,and clarified the interaction between poppet dynamics and sliding friction forces.

The studies mentioned above were concentrated on the flow force analysis and the modeling of the selfexcited vibration including vibration parameter stability,with the aim of exploring the mechanisms and characteristics of valve mechanical vibration.Due to the increasing capability of computational engineering methods(notably with deforming/moving mesh)over the past few decades,the fluid-structure coupling simulation provides the ability to visualize the variation of the internal flow phenomena,and to determine those parameters that are cumbersome to measure during the valve motion simultaneously.Zhang and Engeda(2003) conducted a series of numerical studies on the turbine governor valve to understand the fluid-plug interaction mechanism.It was verified that the asymmetric unsteady flow caused large-amplitude unstable forces and moments,and the FSI was found to be the excitation mechanism that led to plug vibration.Domnick et al.(2015,2017) applied CFD modeling of steam turbine inlet valves to simulate the valve vibration and the feedback to the dynamic flow field.The dynamic responses of the valve plug due to the flow-induced pressure fluctuations as well as the influence of valve plug motion on the flow were investigated.Zeid and Shouman (2019) built CFD modeling of a control valve with different plug shapes using FSI simulation by COMSOL commercial code.A better plug shape was obtained according to the minimum vibration as the fluid flowed through the valve.The results showed a good agreement with both flow and vibration experimental measurements.The FSI simulations of leaflet motion in a heart valve based on the dynamic mesh model were implemented in ANSYS FLUENT by Dumont et al.(2004,2007)and Dahl et al.(2012).After comparing with the experimental data,the FSI simulation in FLUENT provides high-accuracy results although the leaflet motion was considered as a large-displacement problem.Recently,Dong et al.(2015) developed a 2D axisymmetric numerical model with FSI approaches to model the complex phenomenology associated with vibration in a dynamic poppet valve by ANSYS FLUENT.Results showed that the vortices in the flow became unsteady and resulted in pressure variations in the flow field when the multiphase flow was involved.

Cavitation commonly occurs in the fluid flow of a control valve (Qiu et al.,2019;Jin et al.,2020;Li et al.,2020;Liu et al.,2020).It will not only reduce valve efficiency but may also have severe effects on vibration and noise(Kudźma and Stosiak,2015;Qian et al.,2019).Furthermore,cavitation plays an important role in the flow force on the valve disc and consequently results in a variance in vibration characteristics (Yi et al.,2015;Han et al.,2017;Wang et al.,2017).Therefore,it is indispensable to take the cavitation phenomenon into account in the analysis of the fluid force on the valve disc since it plays a crucial role in the creation of valve vibration.On the other hand,cavitation is a pressure-sensitive phenomenon,so the vibration of the valve disc inevitably in turn affects the pressure fields as well as the developing and collapsing of cavities.Accordingly,it is not appropriate to take separate views of cavitation and vibration in valves.However,experimental studies for the cavitation-vibration coupling of cryogenic valves are relatively difficult to conduct and the CFD simulation of the interactions has not yet been studied.Therefore,there is still a research gap for additional efforts to develop a CFD model to study the FSI with cavitation in the cryogenic control valve.

In this study,a 3D CFD model was established to simulate the simultaneous occurrence of cavitation and FSI in the transient vibration of a liquid nitrogen(LN2) poppet-type control valve.The rigidity of the valve stem was considered by prior calculations of the dependence of elastic force on displacement based on the finite element method(FEM).A user-defined function (UDF) for the calculations of the resultant elastic force and fluid pressure force was applied to facilitate the CFD modeling of this complex multiphase cavitating flow and FSI problem.Various conditions of valve openings and pressure differences were investigated to explore the valve disc vibration mechanisms.

2 Numerical methods and physical models

2.1 Geometrical model

Fig.1 is the schematic of the studied two-way poppet-type control valve including the valve stem and valve disc.The nominal diameter,width,and height of the valve are 100 mm,300 mm,and 240 mm,respectively.The valve disc is parabolic in shape and shows linear inherent flow characteristics.The detailed geometrical parameters of the valve stem and valve disc are given in Table 1.

Table 1 Parameters of the studied valve stem and valve disc

Fig.1 Two-way cryogenic poppet-type control valve:(a)overall structure;(b)valve stem and valve disc

2.2 Mathematical model

2.2.1 Governing equations

Numerical simulations of flow through the control valve with cavitation are established at various open states based on the homogeneous mixture mathematical framework,which are solved using the ANSYS FLUENT 18.1.The slip velocity between the liquid and vapor is ignored in the iterative calculations,which implies that both phases share the same velocity.The mixture,including liquid nitrogen and vapor nitrogen,is considered as the working fluid and assumed to be the Newtonian and compressible fluid.The conservation equations of mass,momentum,and energy,and the volume fraction equation for the secondary phases can be denoted as:

(a)Continuity equation:wheretis the time,andρmandvare the mixture density and mass-averaged velocity,respectively.

(b)Momentum equation:

wherepis the local pressure,andμmandμtare the mixture laminar viscosity and the turbulent viscosity,respectively.

(c)Energy equation:

whereTrepresents the temperature.λeffis the effective thermal conductivity(∑αk(λ+λt)),whereαkis the volume fraction for phasek,λis the thermal conductivity,andλtis the turbulent thermal conductivity.hmis the sensible enthalpy expressed ashm=CpT,whereCpis the specific heat.SErefers to the volumetric heat sources,and is determined asSE=hfgR,whereRis the mass transfer rate between phases defined below,andhfgis the latent heat.

(d)Vapor mass transport equation:

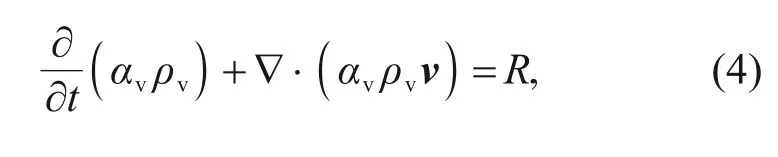
whereαvandρvare the volume fraction and density of the vapor phase,respectively.

The thermodynamic properties,such as the density and viscosity,are defined asΨ=αlΨl+αvΨv,where subscripts l and v represent liquid and vapor phases,respectively.

2.2.2 Turbulence model

Thek-εtwo-equation model has been widely used to simulate the cavitating flow of cryogenic fluids(Hosangadi and Ahuja,2005;Rodio et al.,2012;Zhang et al.,2013).The realizablek-εmodel is employed to obtain the turbulent kinetic energy and the dissipation rate because of its substantially improved capability to characterize flows with acute streamline curvature or vortices when compared with the standardk-εmodel(Zhang et al.,2008).

In the above equations,xjandujare the components of the position and velocity vectors,respectively;Gkis the generation of turbulence kinetic energy due to the mean velocity gradients;vis the velocity;σkandσεare the turbulent Prandtl numbers for turbulent kinetic energykand turbulence dissipation rateε,respectively;SandSijrepresent the strain and mean strain rate,respectively.The turbulent viscosityμtis defined by

whereCμis a model constant and defined as a variable in the realizablek-εmodel.

The constants in the model have the following default values(Yaghoubi et al.,2018):

The enhanced wall treatment is employed to account for boundary layer effects because of its assumption that at the wall-adjacent cells,there exists a local equilibrium between the production of the kinetic energy and the dissipation rate,and better pressure distribution than the standard wall function can therefore be obtained.

2.2.3 Cavitation model

To predict the dynamic cavitation behavior due to FIV in the poppet valve,and also to investigate the effect of cavitation on the valve vibration,the cavitation model proposed by Schnerr and Sauer (2001) is considered in this study,in which the mass transfer rateRbetween the phases in Eq.(4) is expressed in the general form:

whereReandRcrepresent the vaporization and condensation rates per unit volume,respectively,Pis the local far-field pressure,Pv(T) is the saturation vapor pressure,and ℜBis the bubble radius given by

The number of vapor bubbles per volume of liquid (n) in the Schnerr-Sauer model has a significant effect on the cavity characteristics and represents the intensity of the cavitation source.In the present study,the bubble number density is set as 108since it has been verified that the numerical results withnfixed at 108are quite agreed with the experimental data and therefore are more accurate for cryogenic fluids according to our previous study(Zhu et al.,2015).

In addition,the simulations on the cavitating flow of LN2in this study have been well validated in our previously published papers (Zhu et al.,2016;Wang et al.,2019) by comparing the pressure and temperature distributions over the hydrofoil and ogive with experiments(Hord,1973a,1973b).

3 Implementation of the interaction between fluid and structure

3.1 Dynamic mesh method

The unstructured mesh is used to better represent the irregular shape in the control valve domain.The schematic of the volumetric mesh of the studied control valve as well as a sectional view for the volumetric mesh is shown in Fig.2.The geometry is extended to include parts of the upstream and downstream pipes.The lengths of both the upstream and downstream pipes in this numerical model are 200 mm.The grid at the valve disc region is densified to guarantee a high mesh quality despite the motion of the valve disc.The mesh independence is checked by taking the valve opening of 30% with an inlet pressure of 1000 kPa as the checking condition,and the flow rate and the maximum vapor volume fraction are utilized to check the mesh independence.Fig.3 shows the outlet mass flow rate and the maximum vapor volume faction with different grid numbers from 2.9×105to 1.29×106,and the result indicates that the relative variation of flow rate and maximum vapor volume fraction is less than 1% as the grid number exceeds 9.5×105.Consequently,the total number of grid nodes chosen is 946 480 in the model of 30%valve opening,and the same mesh generation approach is applied in other geometry models.

Fig.2 Computational domain and meshing of the control valve:(a)volumetric mesh;(b)sectional view of the mesh

Fig.3 Mesh independence check for different grid numbers:(a)flow rates;(b)maximum vapor volume fractions

The movement of the valve disc is the result of the combined action of pressure in the flow field and the valve stem return force at the beginning of the time step,and correspondingly the velocity and acceleration of the disc can be obtained.Then the followedmotion is determined and realized by employing the dynamic mesh approach according to the resultant force in one time step size.At the end of each time step,the new position and velocity of the valve disc are determined and considered as the starting state for the next time step,and the calculations for the dynamics are repeated based on the same principle.During the calculations,the return force of the stem as a function of the displacement is known and primitively determined by using the FEM before the CFD analysis,which will be explained in detail in the following.In order to implement the dynamic mesh,the combination of a spring-based smoothing method and a local cell remeshing method is used.With the motion of the valve disc body,the grid boundary nodes are relocated to improve the cell quality and the movement of a boundary node is propagated into the volume mesh as a result of the spring force caused by the elongation or contraction of the edges connected to the node.

3.2 Force-displacement relationship of the valve plug

Given that the unbalanced flow force acting on the valve disc mainly exists in the direction vertical to the local flow direction,the movement state and force of the valve disc are analyzed and studied only in thex-direction (Fig.2).The force in thex-direction includes two parts,namely,fluid pressure force and stem elastic force,so the motion equation of the valve disc can be written as

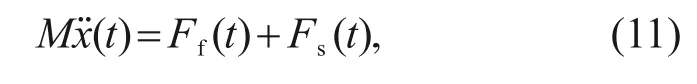
whereFf(t) andFs(t) are the fluid force and elastic force during the valve disc movement,respectively,Mdenotes the mass of the valve disc,andx¨(t) is the acceleration of the valve disc.

The static structural analysis is firstly performed using ANSYS Workbench to obtain the relationship between the displacements and the externally applied forces.The fixed constraint is applied at the other end of the valve stem according to the structure.The force is applied to the valve disc part and has only thexdirection component.The mechanical properties of the valve stem material(type 304 stainless steel),including Poisson’s ratio,tensile and yield strengths,and elastic modulus,are all temperature-dependent.

Under the action of applied forces,the valve stem exhibits elastic deformation to some extent.In addition,the whole disc is considered as a rigid body and its movement is horizontal assuming that the deformation of the stem is small compared with the stem length.Then thexcoordinate of any point in the body can be determined during each time step according to the principles described above.The displacement of a given point in a time step is then determinedrepresents the coordinate of valve disc at time stepk.It should be pointed out that,in consideration of the fact that one does not care about the detailed stress distribution in the stem when it is deformed and the stem is very thin so that its influence on the flow field is small and can be ignored,the valve stem is not modeled in the CFD simulations,while the elastic force exerted on the disc is modeled and realized by implementing the UDF program,in which the elastic force is directly applied to the valve disc.Consequently,the simulation of the fluid-solid coupling is greatly simplified without considering the simultaneous modeling for both the rod motion and the flow field and their interaction through the complex transfer of forces at the interface.Therefore,the maximum displacement of the disc body is characterized by the difference inxcoordinates between the maximum deformation position and original position,which can be denoted as

whereis thexcoordinate of a reference point att=0 in the FSI simulation.

Consequently,the force-displacement relationships are obtained by applying cumulative forces with the same temperature condition of 78 K at one end of the stem and 293 K at the other end to capture the corresponding maximum displacement.The results are illustrated in Fig.4.It can be observed that for small deformations,the relationship between force and deformation is almost linear,which is then implemented into the CFD calculations by developing a UDF code.

Fig.4 Force-displacement relationships of the valve stem

3.3 Computational procedure for FSI simulation

Fig.5 depicts the flowchart that epitomizes the computational procedure applied in this study.The total forces transmitted from the fluid to the structure are obtained by adding the product of pressure and each cell’s projection area normal to thex-direction.The net force is the vector sum of the solid force and fluid force,and is used to determine the velocity and acceleration of the valve disc at each time step.The motion of the valve disc is represented by employing the dynamic mesh,which allows the boundaries of the valve disc to move based on the calculated velocity and acceleration.The mesh is updated at the beginning of each time step and a new solution for the fluid flow is obtained based on the updated(dynamic)mesh.As a result,the FSI is realized.

Fig.5 Flowchart summarizing the computational procedure applied in this study (A:surface area; Ks:coefficient of elastic resistance;Fnet:net force;xref:reference coordinate)

At the end of each time step,the distance between the valve disc and seat is consistently monitored to evaluate whether a strike will occur.The maximum theoretic movable distance for the valve disc is defined by the distance between the seat and valve disc at the initial equilibrium position,which depends on the valve opening.Meanwhile,the direct contact between the valve disc and seat in CFD simulations will generate negative cell volume and result in convergence issues.Hence,the criterion for judging whether a strike occurs is that,if the gap between the valve disc and the seat on one side is less than a relatively small value,the impact is considered to have taken place and the valve disc will move in the opposite direction with the same velocity magnitude in the next time step.

3.4 Solution strategy

The LN2is defined as the primary phase,and the physical properties of LN2and vaporous nitrogen(VN2)are both considered temperature-dependent and obtained from REFPROP 9.1 (Lemmon et al.,2013).The operating pressure is set at 101 325 Pa and the boundary conditions exerted on the valve inlet and outlet are pressure-inlet and pressure-outlet,respectively.The inlet pressure (Pin) varies from 900 to 1000 kPa,and the outlet pressure is fixed at 300 kPa in all states of study.

The time step size of 10-5s is taken and the firstorder implicit scheme is used for time discretization.The pressure implicit split operator (PISO) algorithm scheme is used for the treatment of the pressurevelocity coupling,and a second-order upwind scheme for the discretization of momentum and energy is adopted.The first-order upwind and pressure staggering option (PRESTO!) discretization for the volume fraction and pressure interpolation scheme,respectively,are implemented in the model.Convergence is considered to be achieved when the scaled residuals for mass and momentum are less than 10-3and the scaled energy residual decreases to 10-6.

4 Results and discussion

The FIV characteristics of the cryogenic poppettype control valve with and without cavitation occurrence were compared in the study.To investigate the influences of the pressure difference on the flow and vibration characteristics at various valve stem positions,the pressure difference was varied from 600 to 700 kPa by changing the inlet pressure.Several commonly used lower openings (namely 30%,40%,and 50%),in which pronounced vibration generally occurs,were studied.Correspondingly,the original gap sizes between the valve disc and valve seat are 6.8 mm,9.4 mm,and 12.2 mm,respectively.Note that the maximum movable distance of the valve disc is specified as 0.95 times the initial gap size to avoid numerical errors due to the direct contact between the valve disc and the seat.

4.1 Analysis of cavitation and its effect on the vibration

The cryogenic control valve of 30%valve opening with and without cavitation is firstly simulated.The contours of VN2volume fraction with cavitation in Fig.6 give the evolution of the cavitation distributions with corresponding valve disc displacements in one typical period(Tc)of vibration that accompanies an impact.The total VN2volume caused by cavitation,which represents the intensity of cavitation (Jin et al.,2020;Xu et al.,2019,2020),is also calculated and given in Fig.7.The streamlines,pressure as well as the schematic of the valve flow passage of the middle plane of the valve body are given in Figs.8 and 9 to help understand the cavitation phenomenon.

Fig.6 Contours of the evolution of VN2 volume fraction in a single period of vibration.Note that the displacements of the valve disc corresponding to the specific moments are approximately:(a)Tc/6,5.596 mm;(b)Tc/3,5.114 mm;(c)Tc/2,-0.29 mm;(d)2Tc/3,-5.235 mm;(e)5Tc/6,-5.353 mm;(f)Tc,0.333 mm

Fig.7 Total VN2 volumes (Vv) inside the valve in a single period of vibration

The asymmetric pressure distribution on the valve disc surface finally generates an unbalanced force at the valve natural position (Li et al.,2018).When the unbalanced force coming from the fluid field is larger than the elastic force in thex-direction,the disc will be forced to move.Once the valve instability has been initiated,the valve oscillation strengthens with each cycle until it reaches a limit cycle of pressure (Misra et al.,2002)or impact between the valve disc and the seat occurs.

The transient cavitation behavior is strengthened by the valve disc vibration as recorded at intervals ofTc/6 in Fig.6.Under the action of unbalanced forces,the valve disc moves to the right from the central position ofx=0 tox=5.596 mm within 1/6 cycles,and almost no cavitation is observed when it is at the symmetrical position (x=0).As the disc moves,the right-hand flow area between the disc and seat decreases,leading to an increased local velocity as well as a decreased local pressure (Fig.8a).Finally,the cavitation is initiated as the pressure is below the saturated vapor one,and cavitation on the right side of the valve gradually intensifies.During the next 1/6 cycle,the valve disc encounters an impact with the valve seat and rebounds,and then a relatively large zone of negative pressure behind the disc comes into being and is consequently accompanied by a conspicuously larger cavitation zone and a higher level of cavitation intensity.The results are qualitatively in line with the law of flow.

At the moment of the impact,the throttling area is the minimum,so the pressure in the region behind the valve disc greatly decreases due to the inertia of the fluid,leading to violent cavitation.The total VN2volumes due to cavitation inside the valve increase significantly from about 1000 mm3to exceed 25000 mm3during this time period(Fig.7).After the impact,the disc moves to the left because the directions of the inertia force and elastic force of the valve stem are the same and their sum is greater than the force from the pressure difference.As the right-hand flow area increases,the local flow velocity decreases while the pressure downstream increases,so the attached cavitation is quickly washed away and collapsed,and the total VN2volumes gradually decrease.In consequence,the flow field force in the positivexdirection is decr-eased due to the decreased pressure difference.The incurred cavitation greatly influences the pressure distribution and therefore the load dynamics of the disc.

It is found that when the valve disc comes to stability,it swings back and forth periodically,like a pendulum.After it rebounds from the right hand,it moves to the left to the position ofx=-5.235 mm at the time oft=0.7654 s.It is likely that,with a lower pressure region downstream,cavitation occurs.Meanwhile,no impact on the left-hand seat surface is found,which is attributed to the fact that the elastic force is ultimately greater than the fluid pressure force before the valve disc hits the seat.Therefore,the cavitation intensity and covered area when the disc is far to the left are not as large as when it is far to the right,in which the disc hits the seat.

Fig.8 illustrates the influence of valve disc displacement (due to vibration) on the pressure distribution and velocity of the flow in the valve,with the streamlines colored by the velocity in thex-direction(vx).The inlet and outlet pressures are set constant at 1000 kPa and 300 kPa,respectively.The flow passage area of both sides of the valve is asymmetric due to the disc movement,and the resulting asymmetric flow pattern in turn causes variational pressure distribution on the sides of the valve disc,which determines the fluid force acting on it.The temporal evolutions of pressure distributions of the valve disc are also given in Section 4.2 (Fig.14a).With the valve disc moving far to the right,there is always a sudden increment of velocity along with a sudden decline of pressure in the convergent-divergent section (Fig.9) when the flows pass by the disc and move into the abrupt enlargement behind the valve disc.Meanwhile,the increasing pressure difference between the left and right sides of the valve disc forces it to move further to the right and collide with the seat.In contrast,when the valve disc moves far to the left,the pressure difference as well as the low-pressure zone area is not as significant as that when it is far to the right side because of the flow field constraints.This limitation in the further increase of the pressure difference between the left and right sides of the valve disc explains why the valve disc does not hit the seat on the left side.It can also be observed that a vortex invariably exists in the left side of the valve chamber and there always exists a locality of relatively low velocity.

Fig.8 Pressure distributions and velocity streamlines in a single period of vibration:(a)Tc/6;(b)Tc/3;(c)Tc/2;(d) 2Tc/3;(e)5Tc/6;(f)Tc

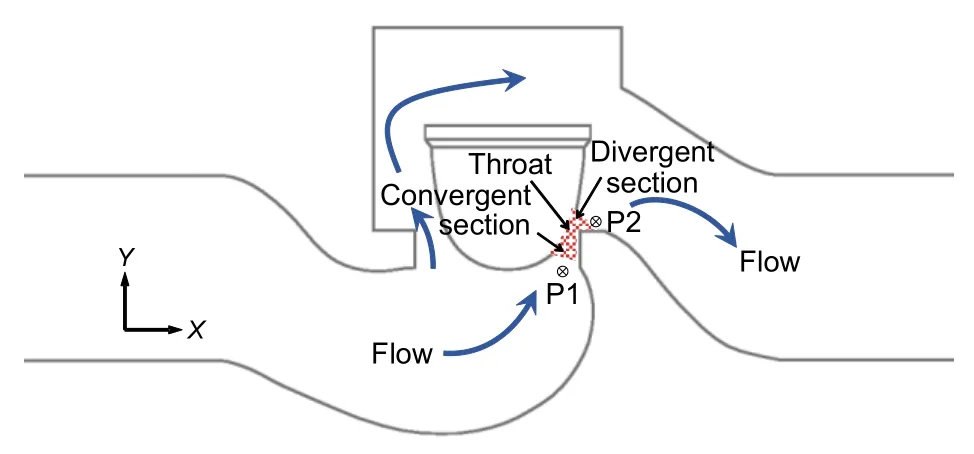
Fig.9 Schematic of the formed throat structure during the process of vibration and the arrangements of the two pressure monitor points in front and behind the valve disc:(1)P1(40 mm,10 mm);(2)P2(50 mm,25 mm)

Simulations for both cavitation and non-cavitation conditions are performed to compare the effects on the valve disc vibration.Fig.10 displays the temporal evolutions of the disc displacement and velocity with or without cavitation occurrence under the same inlet pressure of 1000 kPa within several periods.

The vibration frequency of the valve disc is about 116.6 Hz according to the fast Fourier transform(FFT)analysis of the valve disc displacements with a signal segment ranging from 0 to 1 s.Both the displacement and velocity of the valve disc vary periodically with time.Whether cavitation occurs or not,the valve disc will eventually hit the valve seat (x=6.5 mm) during the vibration process,but the first impact time for cavitation flow is two cycles later than that for the noncavitation flow.It is found in Fig.10a that the movement velocity magnitude of the valve disc for both conditions begins to be the same when the first impact occurs,which corresponds well with the experimental findings (Ferrari and Zachary,2008) that cavitation does not provoke any dramatic increment of transverse force.The final maximum and minimum velocities of valve disc movement with and without cavitation are both around 4.7 m/s and-4 m/s,respectively.

Fig.10 Comparison of temporal evolutions of the valve disc movement with or without LN2 cavitation:(a)displacement;(b)velocity

The comparison of pressure fluctuations of both pressure monitors P1 and P2 with or without cavitation is shown in Fig.11.The pressure variations of P1 and P2 are also featured by the periodic manner for non-cavitation flow due to the reciprocating motion of the valve disc.However,the pressure can increase very sharply for both P1 and P2 when cavitation occurs.The enormous pressure is intuitively caused by the collapse of a large number of cavitation bubbles,and these pressure values can be more than 10 times that of the pressure for the non-cavitation condition.This phenomenon illustrates the strong cavitation erosion of the valve seat or disc,especially at the small opening.As a result,the vibrations will continuously proceed due to the pressure fluctuations caused by the fluid-structure interaction if the opening is kept unchanged.

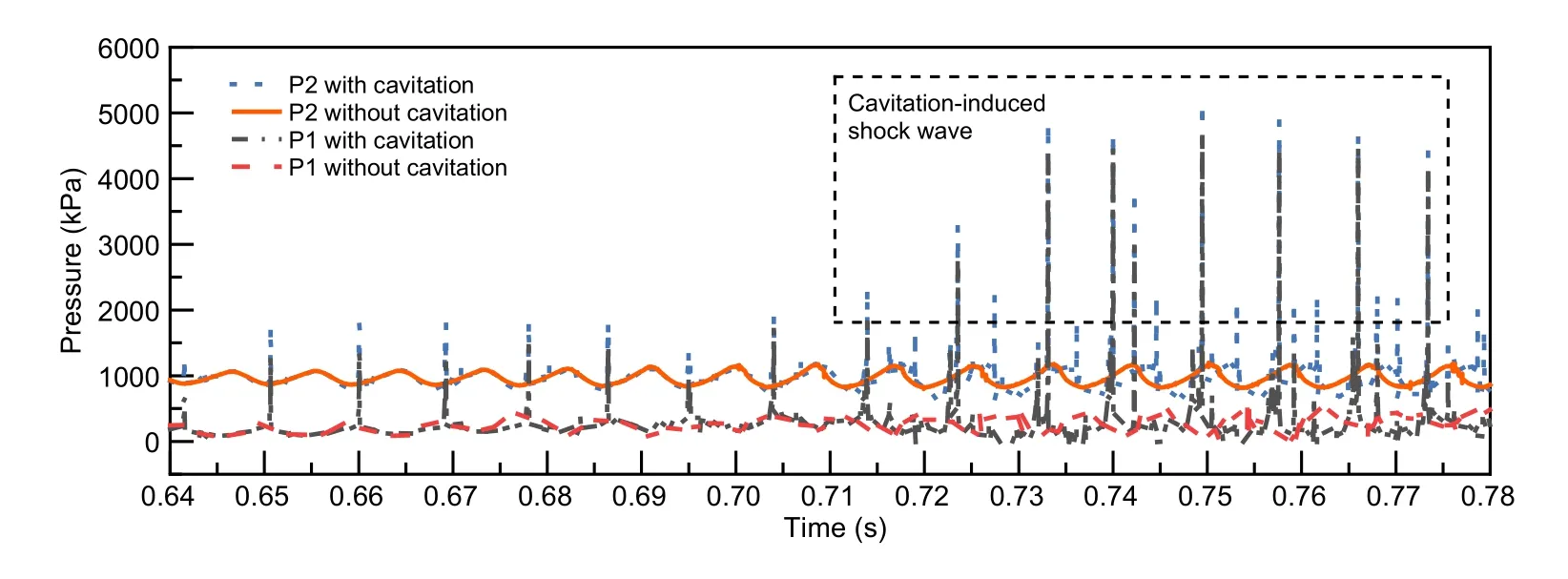
Fig.11 Comparison of pressure fluctuations of both P1 and P2 with or without cavitation occurrence

The amplitude spectra of the pressure for both P1 and P2 are obtained by using FFT with a signal segment ranging from 0.64 to 0.78 s and displayed in Fig.12.A perusal of the spectra suggests that there exists a dominant (peak) frequency at about 114 Hz for both P1 and P2 regardless of whether cavitation occurs or not,and the peak is associated with the largest amplitude for pressure fluctuations.It is found that the largest amplitude for the pressure fluctuations of P1 is larger than that of P2,and increases of 33.91 kPa and 31.24 kPa appear respectively for P1 and P2 when cavitation is considered.Clearly,the pressure at P2 is limited by cavitation,with a minimum of about saturation pressure.

Fig.12 Comparison of the frequency spectra(FFT)of pressure variations with or without cavitation occurrence:(a)P1;(b)P2

Fig.13 displays the impact frequency and impact velocity of the valve disc with or without cavitation.Slightly larger averaged impact frequencies of 119 Hz and greater averaged impact velocities of 1.78 m/s are observed in the absence of cavitation,and the corresponding values are 117.8 Hz and 1.68 m/s when cavitation occurs.The impact frequencies are in accordance with the peak frequency in the amplitude spectrum of the pressure fluctuations for the pressure monitor points(Fig.12).

Fig.13 Comparison of impact frequencies(a)and impact velocities(b)with or without cavitation occurrence

4.2 Parameter effects on vibration and impact characteristics

4.2.1 Effect of pressure difference

Fig.14 illustrates the differences in terms of pressure distributions on the valve disc surface between 700-kPa (Fig.14a) and 600-kPa (Fig.14b) pressure differences in a period of vibration.The pressure distribution on the valve disc is always asymmetric and the pressure magnitude presents distinctive behavior dependent upon the amplitude of the valve disc oscillation.As the valve disc moves to the left,the convergent-divergent section formed between the valve disc and valve seat,creating an upstream relative high-pressure area on the left side of the valve disc surface,and vice versa.Besides,cavitation bubbles generally appear on the upper surface of the valve disc(Fig.8),and hence it can be inferred that the maximum pressure area on the disc surface is also the region to which a tremendous shock wave propagates immediately after the collapse of the cavitation bubbles.

Fig.14 Temporal evolutions of pressure distributions of the valve disc in one period of vibration under different pressure differences for LN2 flow:(a)700 kPa;(b)600 kPa.References to color refer to the online version of this figure

However,cavitation does not contribute dramatically to the transverse force as discussed above.In contrast,the pressure difference has a decisive effect on the fluid force acting on the valve disc.The comparative quantitative description of the temporal evolutions of fluid force acting on the projected area in thex-direction of valve disc is given in Fig.15.For both pressure difference cases,the fluid force follows a sine-like wave form,whose amplitude increases gradually in each cycle until stable cycles are established after the first impact.The maximum fluid forces(x-component) acting on the valve disc at 700-kPa and 600-kPa pressure differences are 1913.5 N and 1646.8 N,respectively.In addition,it is found that the valve disc is subjected to greater fluid pressure forces in the positivex-direction,which validates the observation that the valve disc always initially moves to the right and will not collide with the valve seat on the left side during the vibration period.

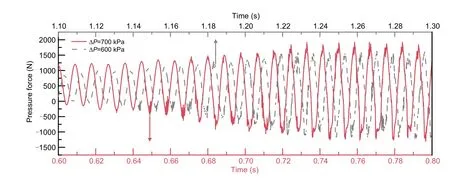
Fig.15 Comparison of temporal evolutions of fluid force acting on valve disc for various pressure differences(ΔP)

Fig.16 depicts the frequency spectra (FFT) of difference,and the highest value of 135.44 kPa is obtained when the pressure difference is 700 kPa.However,the amplitude for pressure fluctuations seems to be less affected when the pressure difference is small,and the amplitude difference is only 1.10 kPa when the pressure difference increases from 600 to 650 kPa.

Fig.16 Comparison of the frequency spectra (FFT) of pressure variations for P1 under different pressure difference conditions

Table 2 lists the first impact times and the corresponding average impact frequencies as well as the impact velocities of the valve disc at different pressure differences.Apparently,the first impact time decreases as the pressure difference increases.For instance,the first impact times are 1.215 76 s and 0.718 96 s at pressure differences of 600 kPa and 700 kPa,respectively.With the comparison of average impact velocities,it is found that the average impact velocity increases as the pressure difference increases,and the value of 1.683 m/s is observed when the pressure difference is 700 kPa.Nevertheless,the average impact frequencies of the three cases are quite close.

4.2.2 Effect of valve opening

Simulations are also performed on the studied cryogenic control valve with 40%and 50%valve openings to explore the effect of valve openings on the vibration characteristics.Fig.17 shows the temporal evolutions of the valve disc movements including displacements and velocities for the two openings (Pin=1000 kPa).Compared with 30% valve opening,the vibration amplitudes and velocities of the valve disc are lowered,and there is no collision between the valve disc and the seat when the opening is 40% or 50%.With the increase of the valve opening,the minimum flow passage area increases,the throttling effect decreases,and the unbalanced fluid force acting on the projected area in thex-direction of the valve disc is reduced.Therefore,the amplitudes of the valve disc vibration decrease.The detailed results are shown in Table 3.

Table 3 The maximum displacements,dominant frequencies,and the corresponding pressure amplitudes for various valve openings

Fig.17 Temporal evolutions of valve disc displacements and velocities for valve openings of 40%and 50%for LN2 flow(Pin=1000 kPa)

Table 2 Average impact frequencies and impact velocities for various pressure differences between valve inlet and outle

The maximum displacements of the valve disc for 40% and 50% openings are 0.65 mm and 0.98 mm,respectively.Smaller displacements correspond to lower vibration frequencies,and both the dominant frequency and amplitude of pressure variations decrease with the valve opening.For instance,the values of dominant frequency and pressure fluctuation amplitude are 114 Hz and 135.44 kPa at 30%opening whereas the corresponding values are 32 Hz and 2.09 kPa at 50% opening,respectively.The immense difference in pressure fluctuation amplitude between 40%,50%,and 30% openings is because of the absence of the pronounced cavitation effect which occurs in the convergent-divergent area formed by one side of the valve disc and seat in the case of minor vibration amplitude.

5 Conclusions

In this study,a 3D CFD model was established to simulate the transient vibration of the cryogenic poppet-type control valve in consideration of the deformation of the valve stem.The simultaneous occurrence of cavitation and FSI was modeled.The CFD simulations were based on the mixture multiphase model.The dynamic mesh technology and the UDFs were incorporated in ANSYS FLUENT to provide a computationally effective methodology for the FSI simulation in the valve.The detailed simulations and consequences of the complicated flow structure interaction in the cavitating flow were presented and analyzed with the following conclusions:

1.The valve disc of the poppet valve periodically vibrates with a frequency of about 116.6 Hz at a valve opening of 30% with an inlet pressure of 1000 kPa.The valve disc will only hit the right seat but not the left seat in the process of vibration within the range of the operating conditions in this study because the valve disc is subjected to greater fluid pressure forces in the positivex-direction.

2.At a valve opening of 30% with an inlet pressure of 1000 kPa,the spectral analysis of the temporal pressure oscillations in the valve shows that there exists a dominant frequency at 114 Hz associated with the peak amplitude of 135.44 kPa for pressure fluctuations when cavitation effects are considered.Lower averaged impact frequencies and velocities are observed with cavitation occurrence as compared with non-cavitation circumstances.

3.Both the pressure differences and valve openings affect the vibration characteristics of the valve disc distinctly.At a valve opening of 30%,the first impact time decreases with the increase of pressure difference,and the average impact velocity increases with the increase of pressure difference.With the increase of valve opening,the collision between the valve disc and seat will not occur and the maximum displacements of the valve disc for 40% and 50%valve openings are both less than 1 mm.The maximum pressure fluctuation amplitudes of 40% and 50%valve openings are far less than that of 30% valve opening due to the absence of the pronounced cavitation effect.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Nos.51636007 and 51976177) and the Key Research and Development Plan of Zhejiang Province(No.2020C01029),China.

Author contributions

Xiao-bin ZHANG designed the research.Ai-bo WEI and Wei ZHANG processed the corresponding data.Ai-bo WEI wrote the first draft of the manuscript.Shun-hao WANG and Rui ZHOU helped to organize the manuscript.Rong GAO revised and edited the final version.

Conflict of interest

Ai-bo WEI,Rong GAO,Wei ZHANG,Shun-hao WANG,Rui ZHOU,and Xiao-bin ZHANG declare that they have no conflict of interest.