PID控制在温度控制系统中的应用研究

苗丽娟

（太原学院 山西省太原市 030000）

温度是一个比较常见的物理量，在生产和生活中随处可见。在工业生产的过程中，温度与产品的质量有着密切的关联，比如在塑料制品的生产过程中，对料筒的温度有着比较高的要求，不同的塑料颗粒需要料筒提供不同温度制成。在大部分应用中，温度的变化过程是非线性的，但是使用PID来控制温度却可以取得比较好的效果,本文分析了在这类系统中，PID是如何能够适应这种工况的。

1 使用电加热圈加热物体时的数学模型

在使用电加热圈时，通常使用PWM波控制在每一个控制周期里加热圈的通电时间，通过不同的占空比（占空比为μ），就可以输出不用的加热功率。加热圈的阻值会随着温度的增加而增加，这样在相同占空比下，加热圈的输出功率就会发生变化。假设加热圈电阻随着温度的变化满足下式：

式中，y为加热圈的温度，R(y)为温度为y时加热圈的电阻，R0为温度为0时加热圈的电阻，k为电阻阻值随温度线性变化时的比例系数。

当某个物体的温度高于所处的环境温度时，温度会逐渐下降，假设温度下降的速度满足牛顿冷却定律：

式中，vy为物体温度的下降速度，k1为温度下降时比例系数，T0为环境温度。

加热圈的加热功率和占空比满足下面的公式：

式中，U为电加热圈通电时的电压。

被加热物体的温度变化率就等于加热功率减去散热功率。

在温度控制系统中，系统都会有滞后，这里假设系统的滞后很小，可以忽略（在实际的控制系统中，可以将较小的滞后等效为一个惯性时间常数比较小的惯性环节）。

2 温度控制系统中的工作点

在生产过程中，有的工艺要求温度随着一个设定曲线随时间变化，有的要求温度保持在一个设定值。在温度控制系统中，当控制加热圈的占空比为一个固定值u0时，被加热物体的温度最终会稳定在一个值y0。这个稳态的点(u0,y0)便是一个工作点，在非线性系统中，只有u在u0附近做小范围变化，同时y在y0附近做小范围变化时，ud=u-u0和yd=y-y0才近似满足线性关系。

假设温度变化过程的非线性动态模型为：

通过泰勒级数展开并截断一阶以上的项，可获得该方程的线性近似。

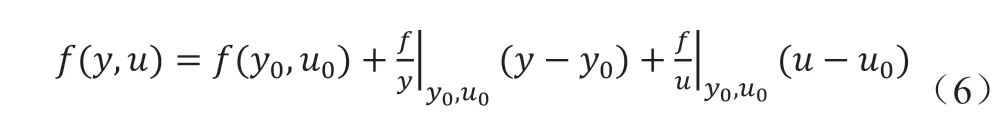
令yd=y-y0, ud=u-u0，可以得到：

针对公式（4），使用公式（5），（6），（7）得到：

对公式（8）取Laplace变换，得到：

式中s为Laplace算子，ys是y的Laplace变换后的值，us是u的Laplace变换后的值。

从公式（9）中可以看出，在工作点附近，yd和ud的关系近似一阶惯性环节。但是在不同的工作点，这个一阶惯性环节的系数是不同的。

根据公式（4），使用Simulink搭建仿真模型。在模型中，R0取值为1，T0为20，k1取值为1，k取值为10，U取值为220，积分环节输出为20。并将下面的模块分装为子系统。被控对象模型如图1所示。

图1：被控对象模型

在0s的时候，系统的输入为0，系统的输出为20。在第1s的时候，系统输入由0变为0.5。在5s左右的时候，系统输出趋于稳定，输出值为46.2。在第7s的时候系统的输入由0.5变为1.0。系统输出跟着输入发生变化，在第10s的时候趋于稳定，系统的输出为80.2。不满足叠加原理，可见系统是非线性的。在阶跃信号下系统响应曲线如图2所示。

图2：在阶跃信号下系统响应曲线

3 使用PID控制

PID控制是一种比较常见的控制方式。PID控制在比例的基础上引入积分，可以消除误差，再加入微分环节，又能提高系统的稳定性[1]。PID控制器本身是一个线性的控制器[2]。

式中，e(k)代表在时刻k,设定值ys与时刻k反馈值y(k)的差，u(k)代表时刻k，PID控制器的输出，kp为比例系数，ki为积分系数，kd为微分系数。

PID控制结构图见图3。

图3：PID控制结构图

因为系统是非线性的，PID是线性的，按照前述分析，PID控制器的使用应该使用工作点附近的相对值（ud, yd），而不应该使用绝对值。但是在实际使用的过程中，并未做这种处理，而是直接使用绝对值，PID仍然可以正常的工作。下面为PID控制器控制非线性系统的分析过程。

如果严格按照在工作点附近线性化的约束。首先应该将系统的设定值，反馈值都转换为相对于工作点y0的相对值，即设定值转换为ysd=ys-y0，反馈值转为yd=y-y0。使用ed(k)=ysd(k)-yd(k)作为PID控制器的输入参与运算。在PID完成计算后，输出控制量应该为PID控制器计算出的ud(k)加上u0以后的值。

通过计算可以看出，PID控制器的输入由于是使用设定值和反馈值的差值。使用绝对值的差值和转为相对工作点的相对值的差值是没有区别的，但输出值应加上u0，应为下式。

在实际使用PID时，并未做这样的处理，而是把PID计算的值直接加到被控对象上面，这是因为PID控制器中有积分环节，这个常量被隐藏在了积分环节之中，PID控制器的积分环节，将系统过去的每个控制周期的误差都保留在里面，这样一个偏置值的存在使得在使用PID的时候，不需要关注工作点，这也是PID的一个优势。在设定值等于y0时，当e(k)逐渐趋近0的时候，积分环节的值会逐渐趋近于u0。当设定值发生变化时，积分环节的存在，使得PID控制器能够找到新的工作点的u0，然后会使得控制器再次工作在局部线性化的线性范围里。正是由于PID使用的设定值和反馈值的差值和引入了积分环节，使得PID具有适应非线性系统的能力。

4 仿真

在实际的控制系统中，被控对象的模型几乎很难使用解析的方法计算出来，在实际应用中，比较多的是通过测量响应曲线上几个点的值来拟合一个已知的模型或者使用模型辨识的方法，如通过给被控对象施加激励（M序列，高斯白噪声等，见图4），记录被控对象的输出，采集最小二乘法估计被控对象的参数模型。

图4：几种用于模型辨识的激励信号

在本文中由于是使用数学建模的方法获得的模型，可以直接计算出系统的模型。

在matlab中使用Simulink搭建公式（10）描述的位置式PID控制器[3]。在u0=0.5, y0=46.2处可以使用公式（9）计算出这个工作点模型为使用临界比例度法计算出kp和ki，kp设置为0.1，ki设置为0.01，kd设置为0，不使用微分环节，控制器的采样时间设置为0.05s，由于控制量u为占空比，变化范围为[0,1],所以PID控制器的输出采用限幅环节，将PID控制器的输出限制在[0,1]的范围内。

使用图5中的控制器控制图1中的被控对象。在0s的时候，系统的设定值为20，系统的输出也是20。在第1s的时候，系统的设定值变为40。在第5s的时候，系统的设定值变为70。在两次设定值变化以后，在PID控制器的作用下，系统的输出达到了设定值。

图5：PID控制器

在系统的输出值由20变化到40的过程中，比例环节的输出，随着设定值和系统输出的误差减小而减小，在系统输出达到设定值的时候，比例环节的输出变为0，积分环节则缓慢增加，在最后系统输出达到设定值的时候，PID控制器的输出就等于积分环节的输出，没有出现超调，积分环节的输出一直在[0,1]的范围内。

在系统的输出值由40变化到70的过程中，比例环节的输出，随着设定值和系统输出的误差减小而减小，由于系统有超调，在系统输出大于设定值的时候，比例环节的计算结果变成了负数，在系统输出达到设定值的时候，比例环节的输出变为了0。积分环节在刚开始的时候增加，由于设定值变化范围比较大，误差积分的时间比较长，在系统输出第一次到达设定值70的时候，积分环节的输出值已经超过被控对象输出在70所需要的值，积分环节的运算特性使得只有系统的输出值大于设定值，才能减小积分环节的输出值，最终的结果是导致超调的出现。超调出现以后，积分环节的输出慢慢减小，在最后系统输出达到设定值的时候，PID控制器的输出就等于积分环节的输出，积分环节的输出超出[0,1]的范围。具体图形见图6。

图6：PID控制下的系统响应

在实际的控制系统中，由于控制器的输出往往是有限的，在设定值出现较大范围的变化时，积分环节会因为调节时间过长而产生积分饱和现象，这是使用带有积分环节的控制器的一个很大的弊端。为了解决这个问题，在工程中可以使用积分分离的控制器，在设定值变化范围较大的时候，在系统输出值与系统的设定值差值比较大的时候，削减积分环节的系数或者直接将积分环节的输入设置为0。

针对这个被控对象使用图7的PID控制器，在设定值与系统输出的误差大于10的时候，积分环节的输入为0。

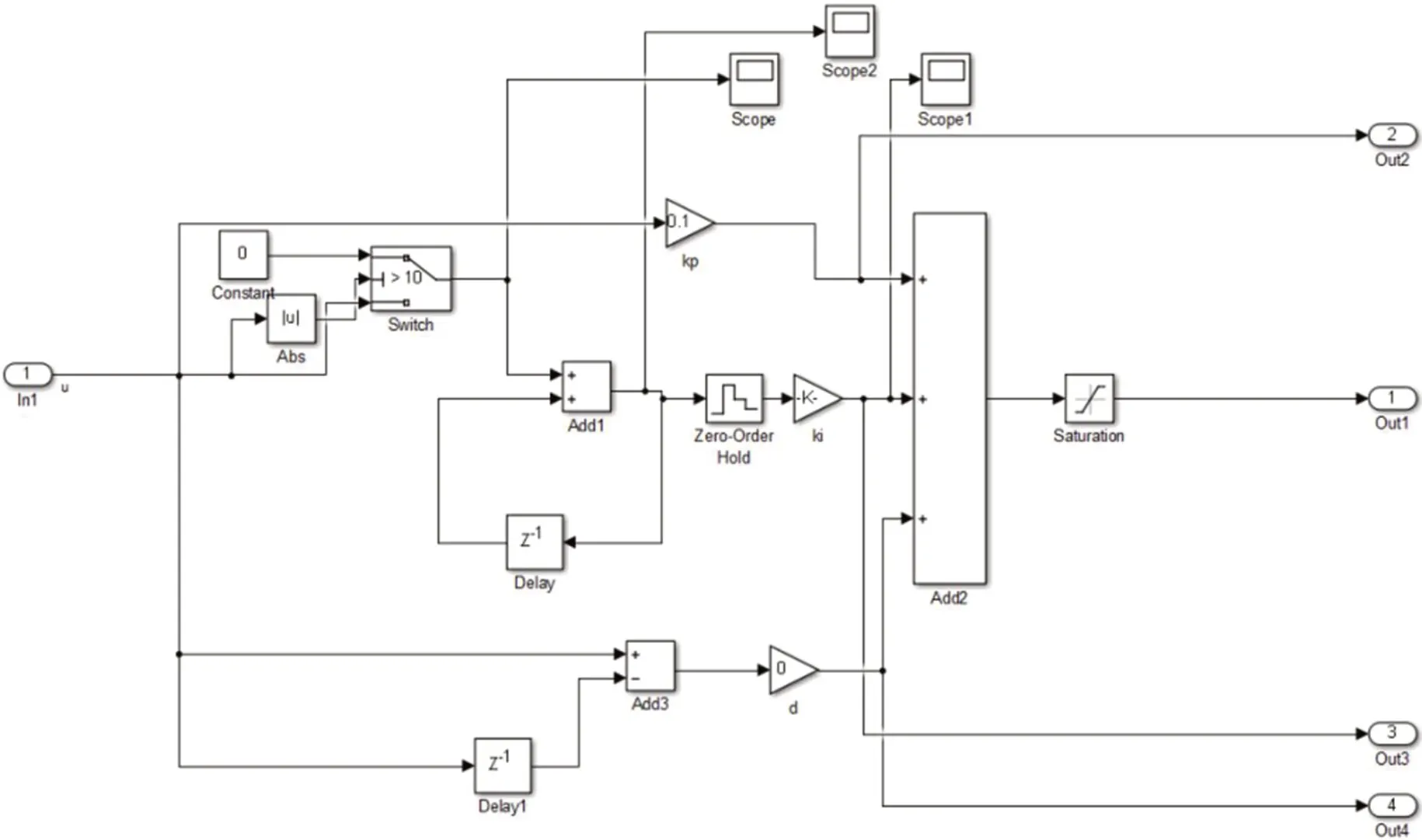
图7：积分分离PID控制器

图8是使用积分分离的PID控制下的系统的响应，在系统的输出值由40变化到70的过程中，积分环节的输出一直保持在[0,1]的范围，没有出现超调，但是因为积分环节的削弱，导致系统的输出需要较长的时间才能达到设定值。

图8：积分分离PID控制下的系统响应

5 结束语

本文使用一个仿真模型说明了PID控制器是如何通过线性的运算来控制非线性系统的，由于PID的特性，人们经常会忽略PID控制器是一个线性的控制器，在工作点做模型估计和控制的时候会使用测量的绝对值而不是基于工作点的相对值做运算，这样得到的模型离实际的模型会有较大误差。在进行PID参数整定的时候，需要使用工作点附近的相对值做运算，在得到PID的参数以后，如果控制系统的设定值有较大的变化，导致PID控制器残生积分饱和的时候，需要采取一定的措施来避免积分饱和的产生，在文献[4]中比较详细的介绍了PID控制的各种改进，也详细介绍了PID使用过程中各种问题是如何产生和如何去解决的。有的系统无法通过数学建模的方法来获取控制系统的参数模型，这就需要使用模型辨识的方法，在文献[5]中有关于模型辨识的详细描述。使用在线实时整定PID参数的方法可以使PID取得的更好的控制效果，文献[6]实时整定PID控制参数用于无人机的控制。