基于秘密共享和压缩感知的通信高效联邦学习

陈律君 肖 迪 余柱阳 黄 会 李 敏

(重庆大学计算机学院 重庆 400044) (信息物理社会可信服务计算教育部重点实验室(重庆大学) 重庆 400044)

随着物联网(Internet of things, IoT)、大数据及机器学习的发展，基于深度学习的技术为我们带来很多便利[1-2]：IoT可以通过传感器设备快速收集环境中的数据，同时具有计算能力的IoT设备可以随时随地参与移动计算[3]；5G可以加快数据的传输速度[4]；移动计算能提供大量的数据处理单元处理数据[5].然而在这些技术发展的背后，大规模的隐私敏感数据正在被泄露.当客户端将数据传输至服务器进行处理时，数据所有权与控制权分离将导致客户端数据有泄露的风险.为了弥补集中式学习带来的隐私泄露问题并充分利用IoT设备收集到的数据，Google于2016年提出了联邦学习(federated learning, FL)[6].客户端在本地训练好数据模型后，只需要将模型参数传递给服务器进行聚合即可，原始数据不离开本地，从而保证了客户端数据的隐私与安全.

然而，近些年的研究发现联邦学习框架中传输的梯度仍然会泄露隐私信息，甚至泄露原始数据[7-8].鉴于此，出现了许多梯度安全聚合的技术，主要包括采用差分隐私(differential privacy, DP)、同态加密(homomorphic encryption, HE)及安全多方计算(secure multi-party computation, MPC)等.但是它们仍然存在各种各样的问题，比如：差分隐私中如何平衡模型准确率及隐私保护是个巨大的挑战；同态加密的计算及通信代价比较高；虽然安全多方计算被广泛用于联邦学习，但标准的安全多方计算算法会存在较大的通信消耗.特别地，McMahan等人[9]指出联邦学习的最大瓶颈是梯度传输过程中产生的大量通信，而基于安全多方计算提供的隐私保护又需要额外的通信代价.在实际应用中，特别是资源受限的设备，难以承受如此巨大的通信负担，故通信时梯度的压缩需要被考虑.因此，深入研究能适用于资源受限环境的、通信高效、有隐私保护且有较好模型性能的算法非常有必要.

为了解决联邦学习中隐私泄露存在的问题，本文完成了2方面的工作：

1) 本文结合压缩感知、1比特压缩感知及安全多方计算中的加法秘密共享技术的优点，提出了2个通信高效的联邦学习算法，使用Top-K稀疏及压缩感知技术同时减少了联邦学习框架中上传和下放数据的通信开销，再利用加法秘密共享技术进一步增强重要梯度参数的隐私性.与现有工作相比，本文算法在降低通信开销的同时保证了数据传输及聚合时的安全.

2) 在常用数据集上进行的图像分类实验结果表明，与近期最新的相关算法[10]CS_FL和CS_FL_1bit以及基线算法FedAvg[9]和SignSGD[11]相比，本文的算法实现了通信开销、隐私保护及模型效率三者的有效平衡.

1 相关工作

本节主要介绍有关联邦学习隐私保护及梯度压缩的现有方案.

1.1 联邦学习隐私保护

为了保证联邦学习框架中模型梯度在传输和聚合时的安全性，现有的方案主要基于3种技术：1)差分隐私；2)同态加密；3)多方安全计算.

差分隐私技术是一种基于噪声机制的数据失真隐私保护技术，在联邦学习训练过程中，通过对需要保护的参数进行噪声扰动，使攻击者无法获取真实参数[12-14].一般情况下，添加的噪声主要是拉普拉斯分布或者高斯分布的噪声.例如，用f(d′)f(d)+来定义拉普拉斯机制，其中用具有拉普拉斯分布的噪声去实现ε差分隐私.但是在基于差分隐私的联邦学习中，隐私预算ε越低，添加的噪声越大，隐私保护程度越强，然而却降低了数据的可用性.如何去平衡隐私与可用性是差分隐私需要考虑的问题.此外，与同态加密及安全多方计算相比，差分隐私无法保证参数在传输过程中的隐私性[15].

同态加密是一种能在密文状态下也可进行复杂计算的加密方法[16-17].Aono等人[18]在逻辑回归的训练过程中使用同态加密保护数据，通过存储及计算复杂度，表明该方法可应用于大规模联邦学习.Hayashi等人[19]提出了一种加同态加密方法，在该方法中，只有拥有解密密钥的参与者才可对更新后的全局模型解密，但其计算代价比较高.Chai等人[20]基于Paillier同态加密实现了安全联邦矩阵分解，但该方法要求客户端必须诚实.虽然同态加密能达到很好的隐私保护效果，但其效率的局限性导致其难以应用于资源受限的环境中.

安全多方计算允许在无可信第三方的情况下设计一个函数，使互不信任的各方在不泄露其原始数据的情况下得到安全输出[21-23]，因此非常适合联邦学习框架中梯度安全聚合的场景.安全多方计算的方式有多种，但考虑到设备资源受限的问题，无法承担混淆电路等方法带来的计算及通信压力，于是本文使用安全多方计算中的加法秘密共享来对数据保密.相比于差分隐私及同态加密，基于安全多方计算的分布式学习[24-26]有较多优势：与基于差分隐私的分布式学习相比，基于安全多方计算的方式不会影响模型聚合精度，也不需要考虑可用性与隐私的平衡；与基于同态加密的分布式学习相比，使用基于加法秘密共享的安全多方计算需要所有客户端联合或一定数量客户端联合[27]才可重构数据，但基于同态加密的方式安全多方计算一般需要假设计算方诚实.

1.2 联邦学习梯度压缩

如引言所述，联邦学习中最大的瓶颈是梯度传输过程中产生的大量通信负载，且随着参数数量的上升，通信开销越来越大.若要用于资源受限的环境，梯度压缩是必要的.针对联邦学习通信开销大的问题，研究者们提出了许多梯度压缩机制，目前主要有3种方式：1)稀疏；2)量化；3)压缩感知.

基于稀疏的梯度压缩方式有多种，Yin等人[28]提出只传输大于某阈值的梯度给服务器，以此减少通信量.Heafield等人[29]提出另一种方式，将梯度进行排序后仅传输前P%的梯度给服务器，其他的存入残差向量.但这些梯度稀疏的压缩只考虑到减少客户端上传局部模型梯度的通信量，未考虑到服务器下发全局模型梯度的通信量.

基于量化的梯度压缩可以压缩联邦学习框架中上传及下发的通信量.最经典的方式是Bernstein 等人[30]提出的1比特量化，客户端只需要上传局部模型梯度的符号给服务器，从而让通信消耗减少了32倍.但Sattler等人[31]指出在非独立同分布(non-independent identically distributed, non-IID)数据集上性能显著下降的问题，并提出稀疏三元化压缩，在梯度传输前通过稀疏、三元化及编码方式对梯度压缩.但是这些量化方式都较为粗糙，导致信息大量丢失，且在non-IID上性能降低较为明显.

相比于传统压缩，压缩感知(compressed sensing, CS)可通过远低于经典的Nyquist采样定理要求的采样频率恢复信号.其大致思想是用满足一定条件的测量矩阵将稀疏或可压缩的高维信号投影到低维空间，然后通过求解一个优化问题高概率恢复信号[32].由于压缩感知的这些优点，其广泛用于信号处理领域，但几乎没有用于联邦学习中.Li等人[10]将压缩感知应用于联邦学习中，并在通信效率及模型准确性上表现出较好的性能.然而文献[10]中的算法每一轮训练均包含2个阶段，且2个阶段都需要客户端与服务器交互，从而造成额外的通信负担.此外，文献[10]将压缩测量值直接传递给服务器，虽然经过压缩感知后的测量值具有一定的安全性[33-34]，但Chen等人[35]指出通过测量值依然会泄露隐私信息.基于上文所述联邦学习存在的瓶颈问题及文献[10]存在的问题，本文提出2个通信高效的适用于资源受限环境的联邦学习，并基于加法秘密共享对传输的重要梯度测量值加密以进一步保证隐私性.

2 基础知识

2.1 联邦学习

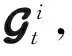
2.2 压缩感知

压缩感知是一个将采样与压缩过程融合成单一感知过程的新颖的框架.在该框架中，若原始信号是稀疏或者可压缩的，则可以仅仅通过少量测量值恢复出原始信号[32].

假设x∈N是一个N×1维信号向量，则压缩感知的采样过程可描述为

y=Φx,

(1)

其中y∈M是通过将信号x左乘一个测量矩阵Φ∈M×N得到的测量值向量.若原始信号不是稀疏的，则需要利用稀疏基对原始信号x进行稀疏表示，即x=Ψs，其中Ψ为一个N×N的稀疏基矩阵，且Ψ与Φ不相关.因此，若感知矩阵ΦΨ满足约束等距性，则稀疏信号s可通过解决如下的1最小化问题来重构.

(2)

其中‖·‖1表示1范式.得到稀疏信号后，可通过得到原始信号.

2.3 安全多方计算

安全多方计算是一种不需要可信第三方参与的协议.假设在协议中有n个拥有私有数据D1,D2,…,Dn的参与者P1,P2,…,Pn，参与者可以合作计算公开函数P(D1,D2,…,Dn)，且在满足计算正确性的同时保证私有数据的保密性.安全多方计算的概念最早由Yao[36]于1982年提出.

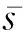
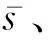
1) 随机选择n-1个随机数：

(3)

2) 计算第n个秘密份额：

(4)

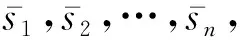
(5)

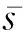
3 算法设计

在本节中，基于压缩感知及安全多方计算，针对联邦学习中存在的通信开销大、隐私泄露及设备资源有限等问题，提出了2个基于压缩感知及安全多方计算的安全高效联邦学习算法——ICFM算法和ICFM_1bit算法.下面，首先介绍2个算法的整体框架，接着给出框架内的2个算法的详细步骤.

3.1 算法框架

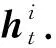
Fig. 1 Our algorithm architecture图1 本文算法框架

3.2 ICFM算法

ICFM算法的伪代码如算法1所示.

算法1.ICFM算法.

输入：初始化的模型参数G0;

输出：优化后的模型参数GT+1.

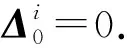
① fort=0,1,…,Tdo

② 随机选择集合M⊆C,|M|=m;

③ for 1≤i≤min parallel do

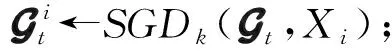
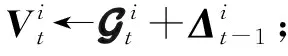
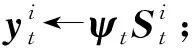
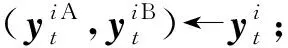
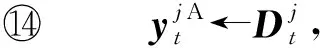
个客户端;

每个参与的客户端Ci基于本地的数据集Xi以及当前梯度Gt执行k次梯度下降法得到更新后的局部模型，表达式为

(6)

(7)

从而弥补稀疏处理导致的模型精度误差下降问题.基于式(7)计算局部模型变化值

(8)

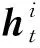
(9)

(10)

使用随机测量矩阵ψt∈M×N对稀疏化后的梯度变化值压缩成测量值，此过程表达式为

(11)

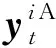
(12)

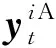
(13)

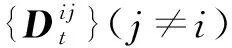
(14)

(15)

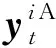
(16)

(17)

(18)

其中wt为学习率.

3.3 ICFM_1bit算法

ICFM_1bit算法与ICFM算法较为相似，伪代码如算法2所示.被选中的客户端Ci基于本地的数据集Xi以及当前梯度Gt执行k次梯度下降法得到

(19)

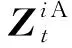
(20)

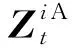
(21)

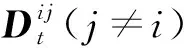
(22)

(23)

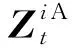
(24)

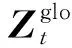
(25)

基于式(25)，每个客户端更新全局模型：

(26)

其中ut为学习率.

算法2.ICFM_1bit算法.

输入：初始化的模型参数G0;

输出：优化后的模型参数GT+1.

① fort=0,1,…,Tdo

② 随机选择集合M⊆C,|M|=m;

③ for 1≤i≤min parallel do

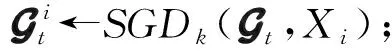
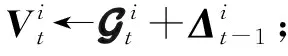
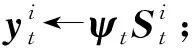
给每个客户端;

4 算法分析

本节对本文所提出的算法进行正确性及安全性分析.

4.1 正确性分析

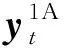
4.2 安全性分析

本节主要讨论本文所提算法是否能保证梯度传输及聚合的安全性.如引言所述，压缩感知本身具有安全性[33-34]，但经过压缩感知后的梯度测量值仍然可能由于能量的泄露导致隐私信息泄露.另外，Sotthiwat等人[41]指出，相比CNN中其他层，第一隐藏层中的参数包含更多原始数据信息，更容易泄露隐私信息.因此，为了权衡通信效率与安全，本文只对A类梯度(第一隐藏层梯度)测量值加密.我们不直接传递A类压缩梯度参数，而是将其分成m份秘密份额并将其他m-1份分发给其他m-1个客户端，此时每个客户端仅拥有自己的A类梯度测量值的一份秘密份额，以及m-1份来自其他m-1个客户端的秘密份额.客户端将自己拥有的秘密份额组合起来代替自己原有的A类梯度测量值，并将更新后的A类梯度测量值传递给PS.

首先我们分析仅加密训练网络的第一隐藏层的参数是否可以保证安全性.由于第一隐藏层参数最接近原始图像，且Sotthiwat等人[41]经过实验证明，相比于其他层，第一隐藏层能触发最大的图像均方误差(mean squared error, MSE)，因此其中包含更多的原始图像信息且更为敏感.另外，在对MNIST数据集图片进行训练时，实验证明仅加密网络第一隐藏层参数足以保护图片隐私安全.因此，本文在对已具有压缩感知自身安全性的梯度测量值上，再对易泄露隐私的A类梯度测量值加密，进一步保证了传输梯度测量值的安全性.

其次，我们在半诚实外部敌手攻击情况下或者在算法参与方为半诚实敌手情况下，形式化分析本文所提算法是否能保证A类梯度测量值的安全性.由于所提算法1与算法2中的A类梯度测量值的安全性均基于加法秘密共享，因此我们仅以算法1为例对安全性进行分析.

定理1.在不超过m-2个客户端及服务器被外部半诚实敌手腐化的前提下，本文所提算法能够保证敌手无法获得关于诚实客户端真实A类梯度测量值的任何信息.

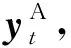
(27)

其中honest代表未被腐化的诚实客户端的集合，而corrupted代表被腐化的客户端集合.至少有2个诚实客户端的梯度之和无法得到具体的某个诚实客户端的真实A类梯度测量值.

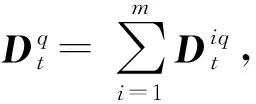
证毕.

定理2.在不超过m-1个客户端合谋的前提下，任意客户端i无法知晓其他客户端的真实A类梯度测量值，服务器无法得到某个具体客户端真实A类梯度测量值.

(28)

根据加法秘密共享的性质，由于无法得到客户端j处的第j份秘密份额，则无法获得关于客户端j的真实梯度测量值的信息.

其次，我们考虑服务器为半诚实敌手的情况.服务器从客户端i处得到更新后的A类梯度测量值为

(29)

而客户端i真实的A类梯度测量值为

(30)

因此服务器得到的并不是客户端i真实的A类梯度测量值，而是每个客户端第i份秘密份额之和，故服务器只能最后得到所选m个客户端A类梯度测量值之和，无法得到某个具体客户端真实的A类梯度更新测量值.

证毕.

5 实验与结果

在本节中，我们对本文所提的ICFM算法及ICFM_1bit算法性能进行了分析，主要包括在经典的MNIST数据集[42]与Fashion-MNIST数据集[43]上对图像分类任务准确率的测量，以及在训练时对通信开销的评估，并对比了近期最新的相关算法(CS_FL和CS_FL_1bit)[10]及基线算法(FedAvg和SignSGD)[9,11].实验结果表明，本文所提算法更具优越性.其中ICFM，CS_FL与FedAvg传给服务器的数据均为梯度测量值或者原始梯度值，而ICFM_1bit, CS_FL_1bit与SignSGD传给服务器的数据均为梯度测量值或者原始梯度值的1比特量化数据.为了公平，以下性能分析主要将非1比特与1比特这2类算法分开比较.

我们在Apple M1 CPU with 3.20 GHz 16 GB RAM 平台上进行实验，采用Pytorch作为机器学习训练库,并利用Python3实现安全多方计算、Top-K稀疏以及压缩感知算法.本文采用的CNN模型是一个6层的网络模型，包含2层卷积层、2层池化层及2层全连接层，卷积核的大小均为5×5.数据集MNIST是包含60 000个训练图像及10 000个测试图像的0～9的手写数字，而Fashion-MNIST数据集是包含60 000个训练图像及10 000个测试图像的共10个类别的图像，类别包含T恤、牛仔裤、外套、裙子等.实验中，我们假设一共有100个客户端，通过frac的值调节参与迭代计算的客户端的数量，客户端对图像进行训练时采用动量为0.5的SGD优化器.

5.1 模型准确率

为了比较本文所提算法与现有算法的准确率，我们考虑了在MNIST及Fashion-MNIST数据集上独立同分布(IID)与非独立同分布(non-IID)数据的算法性能.在本文提出的算法上，我们设置稀疏等级l=0.05，压缩率samplerate=0.1，多次测试不同学习率下的算法性能，并选择最优学习率进行实验.

首先，我们在MNIST数据集上客户端参与率Cp=0.3时测试了不同算法的分类准确率.在IID情况下，如图2(a)所示，我们观察到由于FedAvg传输的梯度原始数据未对其数据进行压缩量化，故其分类准确率无疑最高，大概收敛在99%.而SignSGD准确率最低，大概在96.96%，可能由于其未对数据预处理而粗暴量化造成.CS_FL算法与ICFM算法的分类准确率与收敛速度比较接近，CS_FL_1bit算法与ICFM_1bit算法的分类准确率与收敛速度较为接近，但图2(a)左图放大为图2(a)右图，可以发现本文所提的ICFM算法的收敛速度稍快于CS_FL算法，且最后收敛准确率比CS_FL算法高0.2%.同时，本文所提的ICFM_1bit算法比CS_FL_1bit算法的收敛速度稍快且准确率高0.12%左右，但ICFM_1bit算法与CS_FL_1bit算法性能均高于SignSGD的性能.在non-IID情况下，如图2(b)所示，FedAvg准确率最高且收敛速度最快，ICFM算法比CS_FL算法收敛速度稍快且准确率高0.12%.而ICFM_1bit算法性能远好于CS_FL_1bit算法，本文所提ICFM_1bit算法收敛速度明显快于CS_FL_1bit算法且准确率比CS_FL_1bit算法的最高准确率高1.2%，另外CS_FL_1bit算法震荡较大，比基线SignSGD最高准确率高2.7%.另外，我们发现在non-IID情况下，本文提出的ICFM_1bit算法在前期收敛速度略低于ICFM算法，但最后准确率收敛值几乎相同且准确率收敛值非常接近基线FedAvg，表明本文所提的ICFM_1bit算法在MNIST数据集non-IID情况下能在通信代价更低的情况下保证分类准确率与ICFM算法及FedAvg相差不多.

Fig. 2 Classification accuracy on MNIST dataset图2 MNIST数据集上的分类准确率

Fig. 3 Classification accuracy on Fashion-MNIST dataset图3 Fashion-MNIST数据集上的分类准确率

接着，我们在Fashion-MNIST数据集上客户端参与率Cp=0.3时测试了分类准确率.在IID情况下，如图3(a)所示，FedAvg准确率及收敛速度依然最快，但本文提出的ICFM算法收敛速度仅次于FedAvg且最后准确率仅差0.8%，ICFM算法相比于CS_FL算法收敛速度更快且最终收敛准确率高1.8%.与此同时，ICFM_1bit算法相较于CS_FL_1bit算法，收敛速度略快且准确率高1.2%左右，而SignSGD算法依然是所比较算法中收敛速度最慢且准确率最低的一个算法.在non-IID情况下，为了更加清楚地展示实验结果，我们将传递梯度测量值或者原始梯度值的算法ICFM,CS_FL与FedAvg展示在图3(b)中，而将传递梯度测量值或者原始梯度值的1比特量化数据的算法ICFM_1bit,CS_FL_1bit与SignSGD展示在图3(c)中.从图3(b)中我们观察到，ICFM,CS_FL与FedAvg分类准确率曲线走向比较相近，但本文提出的ICFM算法在前期收敛速度略快于CS_FL算法，且准确率高1.3%左右.从图3(c)中我们发现，3个算法振幅都比较大，但本文所提ICFM_1bit算法优于CS_FL_1bit算法及基线SignSGD算法.

图4展示了在MNIST数据集上不同参与率情况下的分类准确率.图4(a)表示在IID情况下不同算法在不同参与率情况下测试准确率.我们发现，当参与率由0.1上升为0.3时，除了SignSGD外，其他算法的准确率均有不同程度的上升，特别是CS_FL_1bit算法上升幅度达到4.7%，表明参与率的值对算法CS_FL_1bit影响最大.图4(b)表示基于non-IID的情况，从中我们发现参与率由0.1变到0.3时，ICFM,CS_FL与FedAvg算法准确率有不同程度的增加，但是ICFM_1bit,CS_FL_1bit与SignSGD算法准确率却有不同程度的下降，这表明在non-IID情况下，相比于参与率为0.3，参与率为0.1更适合于1 bit类型的算法.

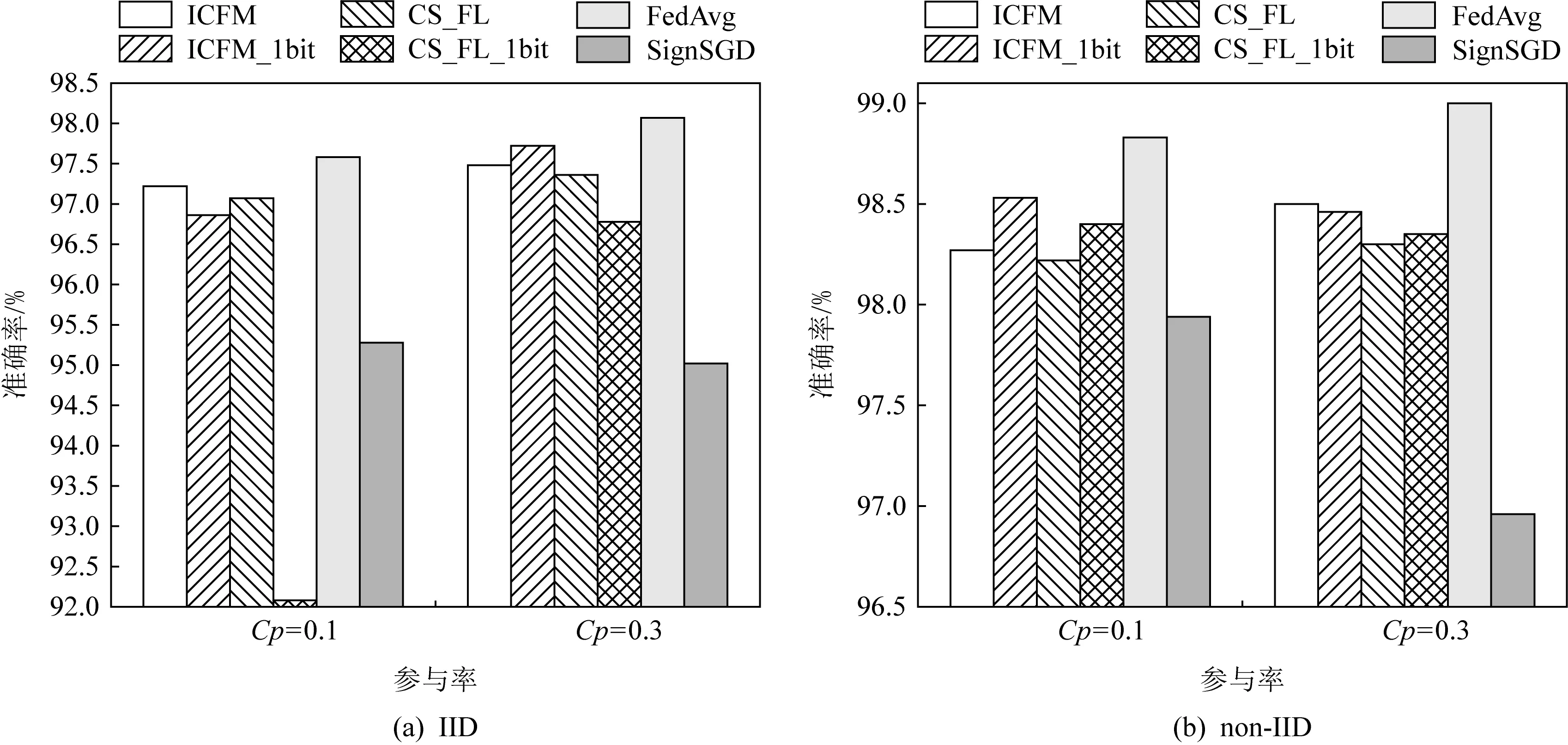
Fig. 4 Classification accuracy on MNIST dataset with different participation rates图4 不同参与率情况下MNIST数据集上的分类准确率

5.2 通信效率

由于联邦学习中通信的消耗主要受参与通信的客户端数量、模型参数的个数以及执行算法本身的影响，故本节分别基于5.1节用到的6层CNN网络以及更复杂的VGG16网络[44]测试了在不同算法下的通信消耗.

如图5所示，在6层CNN网络上，由于模型参数较少，总体的通信消耗在参与者个数为64时也少于6 MB，图5左图中FedAvg由于传输的原始梯度没有经过压缩量化等，故通信消耗几乎成指数性增长.本文提出的ICFM算法及ICFM_1bit算法虽然经过秘密共享技术保证重要梯度测量值的安全，然而却带来了额外的通信代价，但由于并没有对所有梯度参数加密，故带来的通信代价可接受，另外，在参与者个数较少时，ICFM算法与CS_FL算法的通信代价几乎相同.并且，未用秘密共享的ICFM算法——ICFM_NMPC在参与者个数为32时比ICFM算法减少了0.1 MB，同时比CS_FL减少了0.01 MB.因此，本文所提ICFM算法未加安全性时比CS_FL高效，增加安全性后通信消耗也可接受.与此同时，我们发现所提出的ICFM_1bit算法随着参与者个数的增加，通信消耗比CS_FL_1bit算法通信消耗更少、通信效率更高.由于本文算法在每轮训练只需要与服务器交互一次，但CS_FL_1bit需要交互2次，故本文所提ICFM算法及ICFM_1bit算法用较少的额外通信消耗收获了更强的安全性，在6层CNN网络上，本文所提算法相比其他算法有较好的性能.

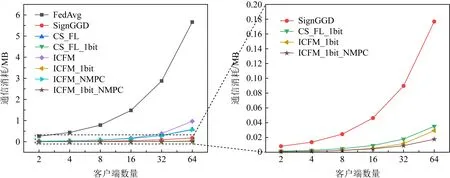
Fig. 5 Communication cost in CNN with various client numbers图5 不同客户端数量情况下在CNN网络上的通信消耗

图6为在更为复杂的VGG16网络上针对不同的算法的通信消耗分析.如图6左图所示，本文所提的ICFM算法在较为复杂网络中通信消耗几乎与CS_FL一致，这是由于本文只对第一隐藏层网络进行加密，当网络层数越多，对第一层隐藏网络加密带来的额外通信在总通信的影响会越多.从被放大的图6右图我们发现，本文所提ICFM_1bit算法几乎与未用加密的ICFM_1bit_NMPC算法消耗相近，且ICFM_1bit算法通信消耗随着客户端个数的增加比CS_FL_1bit通信消耗更少，且在客户端个数为64时，比CS_FL_1bit降低大约112.4 MB.

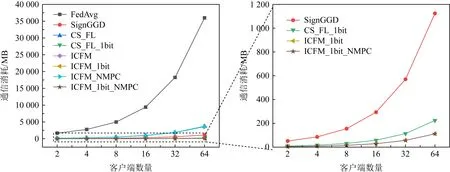
Fig. 6 Communication cost in VGG16 with various client numbers图6 不同客户端数量情况下在VGG16网络上的通信消耗

根据图5、图6可以发现本文所提算法在较为复杂的VGG16网络上与其他算法相比，通信效率更高.在稍简单的6层CNN网络上，本文的ICFM_1bit算法通信效率也比其他算法更高，ICFM算法中安全性保证带来的额外通信消耗也可以接受.综上所述，从性能和安全性2方面综合考虑，本文所提2种算法相比其他算法无疑是最优的.

6 总 结

联邦学习中梯度传输造成的高通信代价成为其重要瓶颈之一，特别在资源受限的环境影响更为严重.同时，保障梯度的安全传输与聚合也成为联邦学习中的重大挑战.本文算法结合Top-K稀疏、压缩感知及多方安全计算的优势，在保证梯度传输及聚合安全的情况下大幅度提升了通信效率.但本文工作也有不足之处，由于本文应用于资源受限的环境，出于对安全和性能的综合考虑，本文采用高效的(n,n)加法秘密共享，需要假设被选择的m个客户端能够成功将自己更新后的梯度测量值传递给服务器，暂时未考虑某些客户端出现掉线、损坏等情况，算法鲁棒性不够强.可能的解决方式有：1)寻找较为高效的(t,n)阈值秘密共享代替加法秘密共享，只要服务器接收到不少于t个梯度测量值份额，则可以恢复计算得到A类梯度测量值；2)采用其他密码学方式对A类梯度测量值进行保护，由于在服务器端只能得到所参与客户端A类梯度测量值之和，而不能得到具体某个客户端A类梯度.在未来工作中，我们将进一步考虑算法鲁棒性问题.

作者贡献声明：陈律君设计研究方案，负责实验，撰写初稿；肖迪参与方案讨论、论文修改及最后定稿讨论；余柱阳采集数据、参与实验研究及结果分析；黄会负责采集、分析数据；李敏负责数据分析及调查.