双金属复合管线应力分析中当量折算模型的建立与应用*

2022-11-12谷天平练章华陈俊文史君林成旭堂

中国安全生产科学技术 2022年10期

谷天平,练章华,陈俊文,史君林,成旭堂

(1.西南石油大学油气藏地质及开发工程国家重点实验室，四川成都 610500；2.中国石油工程建设有限公司西南分公司，四川成都 610041)

0 引言

双金属复合管因兼顾管线建设所需的经济性和耐腐蚀性而被广泛应用于具有腐蚀环境的油气集输系统中，该系统中管线应力分析工作是保障酸性气田集输系统安全的重要保障[1-3]。国内外常用的管道应力分析标准，如GB 50251—2015[4]和ASME B31.8—2020[5]设计规范中详细规定了单层管道系统的温度应力计算方法，然而未对双金属复合管的应力分析方法做出规定，行业内采用的普遍做法是将复合管结构进行简化，仅考虑基管的承压作用而忽略衬管来进行管线应力分析[6-8]。考虑到双金属复合管的基、衬管材料不同，其弹性模量、材料密度和热膨胀系数等参数存在明显差异；在运行压力和温度耦合作用下，基、衬管之间的相互作用较为复杂。这些问题给双金属复合管线的应力分析工作带来很大挑战，因此保障双金属复合管集输系统安全对于酸性气田持续开发具有重要意义[9-13]。

在役双金属复合管线在运行过程中不仅经受管内腐蚀性介质考验，还会受到温度、内压、弯曲和土壤约束等复杂载荷作用[14-18]。Focke等[19]通过实物实验研究复合管系统和基管系统轴向压缩性能的区别；Wang等[20]使用有限元方法研究在轴向压缩载荷作用下基管强度、衬管强度、基管厚度和衬管厚度等因素对双金属复合管结构稳定性的影响；Yuan等[21]研究弯曲载荷对衬管起皱性能的影响，并建立衬管起皱的预测模型。以上研究成果对复合管线的安全运行具有重要作用。然而，这些研究无论是实验研究法、理论解析法还是有限元法都具有一定局限性，无法对复合管线整体受载状态进行完整描述。如一般酸性油气集输管线长度约几公里至十几公里，受地形和环境条件约束，管线铺设状态较为复杂，传统解析法或有限元法对完整管线的应力状态描述存在一定难度[22]。此时，必须借助专业的管道应力分析软件(CAESER Ⅱ，AutoPIPE等)进行完整全尺寸管线建模，研究管道在温度、内压、弯曲和土壤约束等复杂载荷作用下的应力状态。

然而，CAESER Ⅱ软件未设置针对管线类型为双金属复合管的应力分析模块，通常做法是按基管的几何参数进行研究，如：对管外径、壁厚、弹性模量、热膨胀系数等进行管道应力校核时，容易忽略衬管的承压作用，导致计算结果过于保守，造成不必要的管线材料浪费。为此，本文建立1种衬里复合管线应力分析力学模型，利用当量折算方法，将衬管、基管的材料特性和几何参数等量代换为等效管模型，并通过理论分析和有限元计算验证在不同管线状态下，等效管模型在双金属复合管应力分析中的可行性，研究结果可为双金属复合管线应力分析提供新的参考依据。

1 双金属复合管系统受力计算模型

双金属复合管道系统可以看作是2个紧密结合的圆管同轴叠加而成，其中，基管起承压作用，衬管起防腐作用。图1为衬里复合管结构示意，其中D1，D2分别为衬管的内径和外径；D2，D3分别为基管的内径和外径。在实际埋地管道运行过程中，由于管道周围土壤的摩擦约束，部分管段会被完全锚固，不能轴向移动。因此，本文将整个衬管复合管道系统作为研究对象，假设管道总长度为L，可动段长度为x，建立运行状态的双金属管线受力模型，见图2所示。

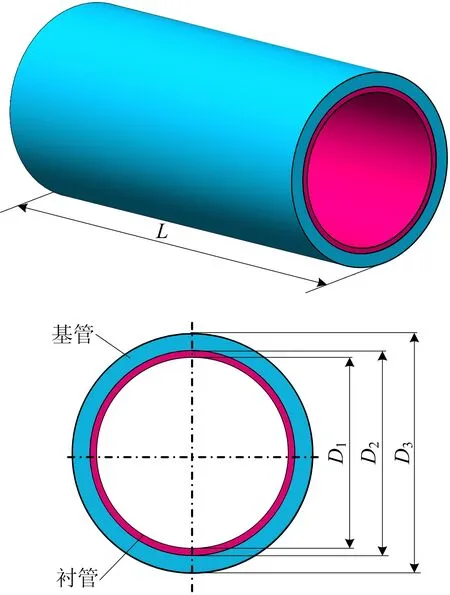
图1 衬里复合管结构示意Fig.1 Schematic diagram for structure of lined composite pipe

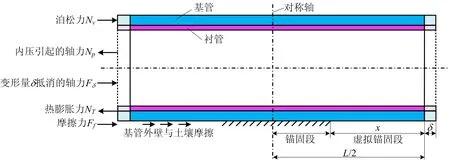
图2 运行状态的双金属管线受力模型Fig.2 Force model of bimetal clad pipeline in operation state

根据管道系统结构的对称性，在对称轴截面的静力学平衡方程[23]如式(1)所示：

NT-Nv+Np-Ff-Fδ=0

(1)

式中：NT为温度变化产生的复合管热推力，N；Nv为复合管材料的泊松力，N；Np为内压所产生的轴力，N；Ff为管外土壤摩擦力，N；Fδ为管道末端由于变形而抵消的轴力，N。

由温度变化产生复合管的热推力NT如式(2)所示：

(2)

式中：NT,1和NT,2分别为温度变化产生衬管和基管的热推力，N；α1和α2分别为衬管与基管的热膨胀系数，1/℃；Td为管线运行温度，℃；Ta为环境温度，℃；A1为衬管截面积，mm2；E1为衬管材料弹性模量，GPa；A2为基管截面积，mm2；E2为基管弹性模量，GPa。

由于复合管材料的泊松效应，内压产生的轴向力Nv如式(3)～(4)所示：

Nv=σh,pA0v

(3)

σh,p=p[D1/(D3-D1)]

(4)

式中：D1，D3分别为衬管内径和基管外径，mm；A0为复合管的截面积，mm2，A0=A1+A2；v为复合管材料泊松比；σh,p为复合管的环向应力，MPa；p为管内压力，MPa。

复合管运行内压引起的轴力Np，如式(5)所示；摩擦阻力Ff根据复合管自重和土壤纵向摩擦系数计算，如式(6)所示：

Np=pA0

(5)

Ff=μWpL

(6)

式中：μ为土壤的纵向摩擦系数；Wp为单位长度复合管的自重，kg/m；L为管长，m。

复合管系统管端位移δ所抵消的轴向力Fδ如式(7)所示：

Fδ=2(E1A1+E2A2)δ/L

(7)

式中：δ为复合管系统管端位移，m。

当温度升高时，复合管的热膨胀力由衬管与基管共同承受，因此复合管的管端应变εt如式(8)所示：

(8)

式中：εt为复合管的管端应变。

由式(1)～(8)可知，复合管系统的管端位移δ如式(9)所示：

(9)

式中：x为虚拟锚固段长度，m。

根据式(9)将式(1)改写为如式(10)～(11)所示：

(10)

(11)

根据以上计算，本文建立的双金属复合管系统受力模型，可以较为准确、快速地求解在运埋地复合管系统的轴向载荷与管线的锚固位置分布。

2 等效管模型的建立

海洋油气集输常用的管中管(pipe-in-pipe)由2种不同外径的碳钢管组成，内外管之间的环形空间填充保温材料，等效管模型在管中管系统的应力分析中是可行的[21]。考虑到在衬里复合管的基管和衬管之间存在初始紧密度，其刚度特性由衬管和基管共同承担。因此，可以建立等效的单层管模型，使其轴向拉压刚度、热膨胀系数和质量等与整体基-衬组合的双金属管道系统相同，从而得到与原复合管系统相同的整体力学效应。

对于整个衬里复合管系统，使用外径为Deq2和内径为Deq1的等效管进行当量折算。由于等效管的横截面应具有与原衬里复合管系统相同的弯曲刚度，可以通过复合管系统惯性矩叠加原理，则等效管截面惯性矩Ieq如式(12)所示：

(12)

式中：I1，I2分别表示衬管、基管的惯性矩，mm4；Deq1为等效管内径，mm；Deq2为等效管外径，mm。

同理，通过叠加横截面积可以获得单位长度等效管的质量和轴向刚度，等效管的横截面积面积Aeq如式(13)所示：

(13)

式中：Aeq为等效管的横截面积面积，mm2；A1和A2分别为衬管和基管的横截面积，mm2。由式(12)～(13)可以推导出等效管内径Deq1和外径Deq2。假设2个中间变量P和Q，推导过程如式(14)～(15)所示：

(14)

(15)

采用同样的方法求解等效管轴向刚度Teq，等效管弹性模量Eeq，单位长度等效管质量me，如式(16)～(17)下：

Teq=EeqAeq=E1A1+E2A2

(16)

me=ρeAeq=ρ1A1+ρ2A2

(17)

式中：Teq为等效管轴向刚度，N/m；Eeq为等效管弹性模量，GPa；me为单位长度等效管质量，kg/m；ρ1，ρ2分别为衬管、基管的密度，kg/m3。

等效管热膨胀系数αeq可由NT求得，如式(18)所示：

NT=EeqAeqαeqΔT=E1A1α1ΔT+E2A2α2ΔT

(18)

式中：αeq为等效管热膨胀系数；ΔT为温差，Td-Ta，℃。

以Φ323.8×(10+3)mmX60-825衬里复合管为研究对象，根据式(12)～(18)求得该规格复合管折算后的参数。表1为双金属复合管与等效管的几何参数对比。

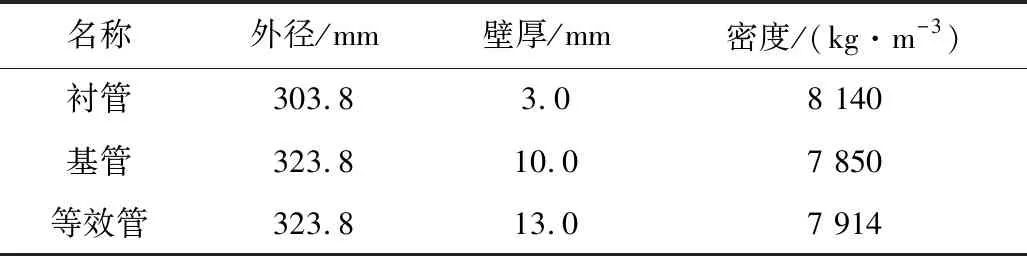
表1 双金属复合管与等效管的几何参数对比Table 1 Comparison of geometric parameters between bimetal clad pipe and equivalent pipe

由式(2)可知，温度是影响管道热膨胀力的主要原因。常用的分析方法在计算时仍然使用单一材料力学参数，当管道温度发生变化时，可能会导致计算误差，温度变化对材料力学参数的影响引起复合管道应力计算结果变化。因此，根据标准B31.8得到受温度影响较大的热膨胀系数和弹性模量值，根据式(16)～(18)计算相同温度下双金属复合管与等效管的材料参数，结果如表2所示。

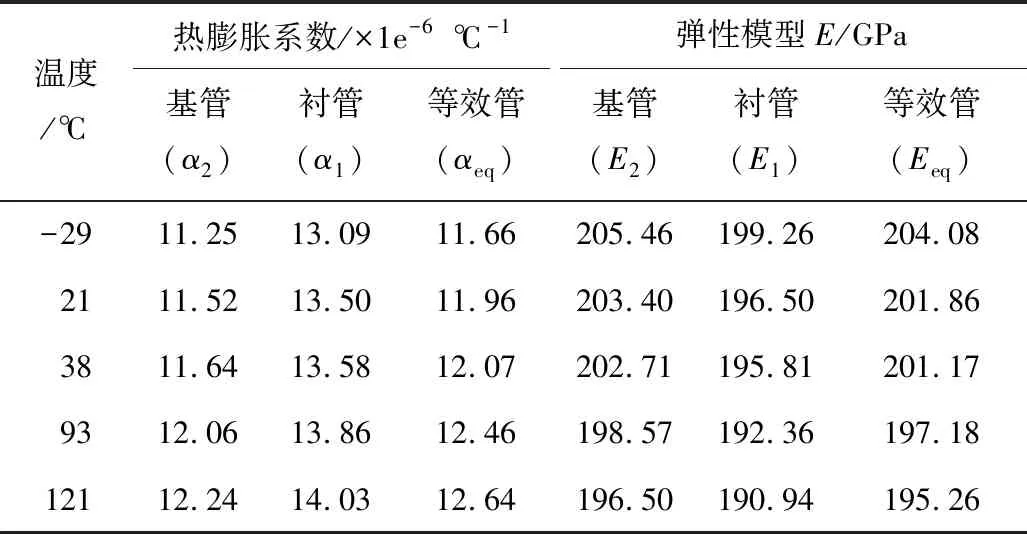
表2 双金属复合管与等效管的材料参数对比Table 2 Comparison of material parameters between bimetal clad pipe and equivalent pipe

利用表1和表2给出的双金属复合管和等效管的参数进行有限元建模计算，验证等效管模型的计算精度。

3 算例分析

3.1 有限元模型建立

为验证应用等效管理论，分析双金属复合管力学响应的合理性，采用有限元方法建立双层复合管和单层等效管的力学模型，以表1中Φ323.8×(10+3)mmX60-825双金属衬里复合管为例，根据管结构特点和载荷条件，分析内压和温度荷载共同作用下的力学响应。建立三维衬里复合管与等效管1/2有限元力学模型，见图3所示。

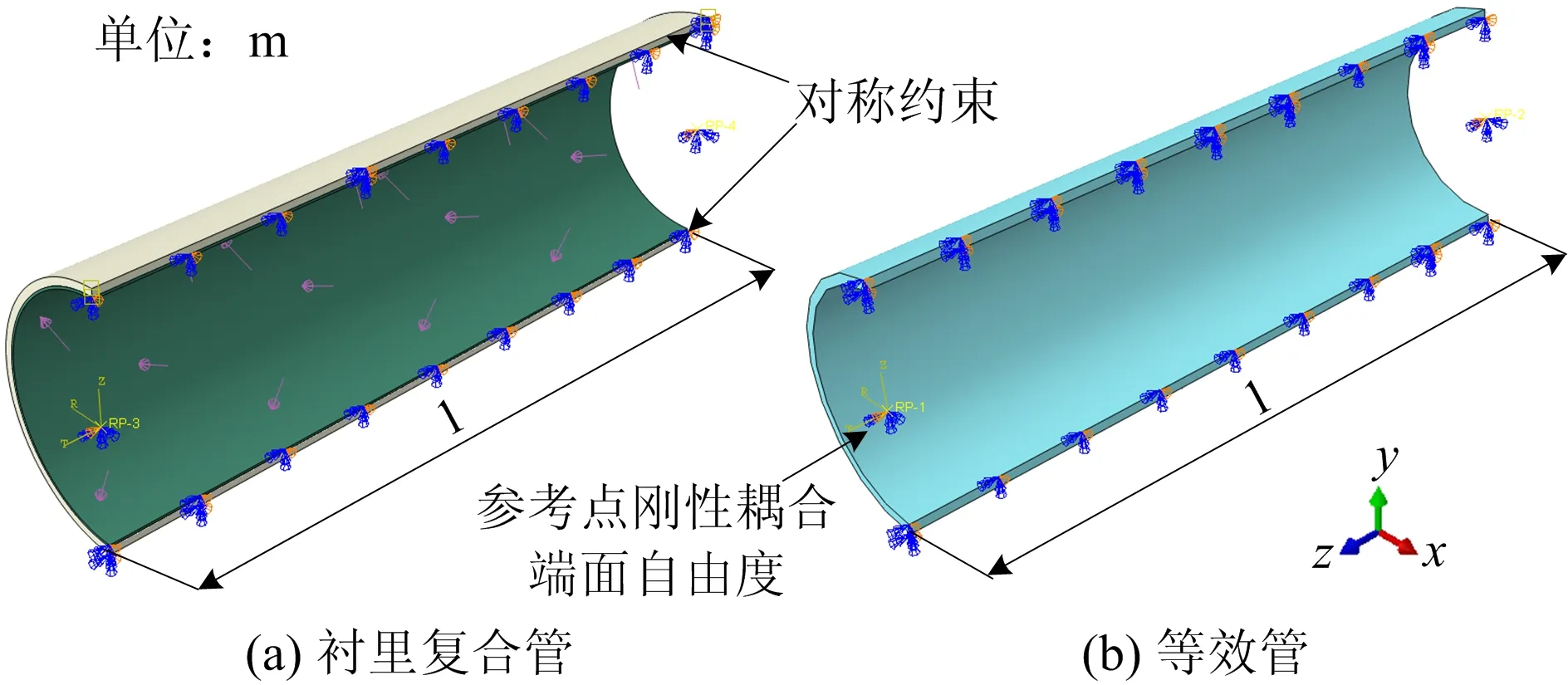
图3 衬里复合管与等效管三维1/2有限元力学模型及边界条件Fig.3 Three-dimensional 1/2 finite element mechanical model and boundary conditions of lined composite pipe and equivalent pipe

图3中2种管模型的分析长度均为1 m，且管端均采取端面自由度刚性耦合方式，将其绑定于各端面所在的圆心参考点处，并限制参考点Z向位移，通过提取各参考点Z向计算结果获取管道轴向载荷。在图3(a)复合管模型中衬管与基管之间定义接触对，并设置基管内表面为主面，衬管外表面为从面，设置接触面间摩擦系数为0.3，接触算法为罚函数法。在2种管1/2有限元力学模型的YZ平面上施加对称约束。2种模型网格密度如下：轴向均布50个单元，环向均布45个单元，径向均布13个单元，总共29 250个三维实体单元，单元类型为C3D8R。

3.2 轴向载荷计算结果对比

对不同运行工况下2种管模型的计算结果进行对比，将此次有限元分析的加载过程分为2步：升温过程和加压过程。第1步，将2种模型的运行温度由20 ℃线性增加到90 ℃，分析因温度升高导致的材料弹性模量与热膨胀系数等参数变化下，2种模型的力学响应误差对比。第2步，在升温的基础上施加管内压力，从0 MPa线性增加到14 MPa，对比由于压力升高，材料弹性模量与泊松效应对2种管模型力学响应的影响。2种管模型有限元Mises应力计算结果如图4所示。

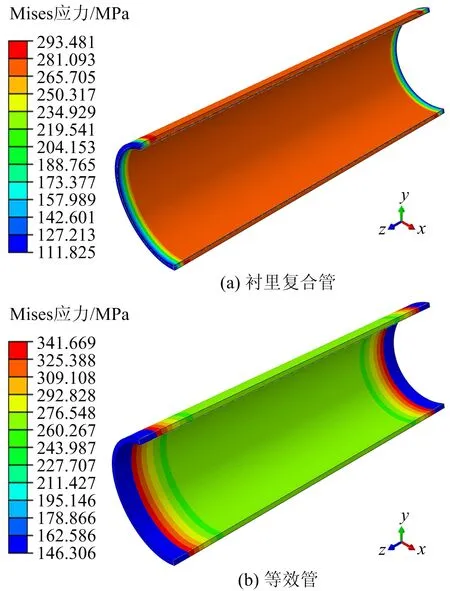
图4 衬里复合管模型与等效管模型Mises应力计算结果Fig.4 Results of Mises stress calculated for lined composite pipe model and equivalent pipe model

图4中为提取管端的轴向力，在模型z轴进行约束，因此Mises计算结果中靠近管端部位小范围内有应力突变。提取2种管模型在加载过程中的轴向载荷变化过程进行对比，利用式(1)、表1和表2中的具体参数计算出对应工况下的解析解，计算结果对比如图5所示。

由图5中可以看出，在升温与增压过程中，2种管有限元模型的计算结果非常接近。提取第2个分析步结束时的轴向力结果，其中衬里复合管模型、等效管模型和解析解计算结果分别为1 899.57 kN、1 896.92 kN和1 898.82 kN，2种有限元模型与解析解的计算误差分别为0.40%和0.10%。由此可见，当量折算方法应用于衬里复合管模型求解轴向力时，其计算误差较小，可以在一定程度上满足工程应用。

3.3 不同工况误差分析

为了更加全面地评价在不同工况下2种管模型的分析误差，提取管线运行过程中4种典型工况，分别代表管线实际运行过程中停运、低压、中压和高压工况，见表3所示，对4种工况下衬里复合管环向、径向、轴向、Tresca应力和Mises应力进行综合评价，充分讨论2种模型的计算误差对比结果，见表4所示，表4中单位均为%，对误差>1的参数未表示。

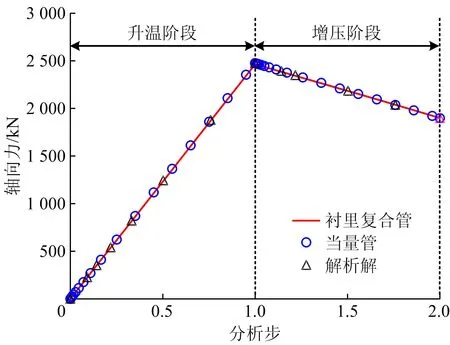
图5 温压耦合作用下衬里复合管与等效管轴向力有限元与解析解计算结果对比Fig.5 Comparison on calculation results of finite element and analytical solution of axial force between lined composite pipe and equivalent pipe under thermo-pressure coupling

表3 衬里复合管运行阶段的4种典型工况Table 3 Four typical conditions of lined composite pipe during operation

表4 不同工况下等效管较衬里复合管模型应力误差对比结果Table 4 Comparison of stress analysis errors between two pipe models under different conditions %

由表4可知，虽然2种管模型在内壁环向应力、外壁径向应力和内外壁轴向应力分量评价指标上误差较大，这是因为此时的管内压力较小而温度较高，复合管基衬材料热力学性质差异导致衬管和基管相互作用力较大。但是Tresca应力和Mises应力计算结果误差值较小且分布稳定，2种管模型Tresca应力误差最大值为-1.81%，最小值为0.31%；Mises应力误差最大值为4.95%，最小值为0.03%。由此可见，在使用等效理论将双层衬里复合管转化为等效单层管进行应力分析时，推荐使用Tresca屈服准则或Mises屈服准则来评价等效管应力水平，其计算误差较小。通过对不同工况下2种管模型应力误差分析，进一步验证了等效管模型具备一定的合理性和准确性，可为实际工程应用提供可参考的理论基础。