基于卷积神经网络的冲击地压预警方法研究*

2022-11-12曹亚利李振雷刘旭东何学秋宋大钊王洪磊

中国安全生产科学技术 2022年10期

曹亚利，李振雷，刘旭东，何学秋，宋大钊，王洪磊

(1.北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083；2.北京科技大学土木与资源工程学院，北京 100083；3.北京科技大学大安全科学研究院，北京 100083；4.国家能源集团新疆能源有限责任公司，新疆乌鲁木齐 830084)

0 引言

冲击地压是煤矿开采中1种常见的动力灾害，是指煤(岩)体聚积的弹性变形能瞬时释放而产生的1种动力现象，常造成巷道破坏、设备损毁以及人员伤亡等[1-4]。冲击地压预警技术在矿山灾害防治方面有重要作用，是提高冲击地压防治水平的关键[5]。目前，越来越多的先进设备被用于矿山开采中，以微震、地音、电磁辐射为代表的监测手段得到普及[2,6]，针对这些监测手段的冲击地压预警方法众多。Cai等[7]提出了1种基于模糊综合评价模型的冲击地压预测方法，利用混淆矩阵的绩效指标F确定预警指标的权重，可以对冲击地压发生的可能性进行定量预测；田向辉等[2]通过分析冲击地压微震前兆信息规律，提出了1种基于每日微震最大能量和微震能量/频次偏差高值总数的定量-趋势的冲击危险预警方法；殷欣等[8]从岩石物理力学性质、岩体完整性和地应力3个方面选取岩爆的评价指标，提出1种基于离差平方和的最优组合赋权规则，建立了岩爆烈度分级预测识别模型。现有的冲击地压预警常采用经验类比或数理统计的方法确定预警指标和判别准则，以此对冲击地压危险进行预测[3,9]。但采用指标法进行冲击地压危险预警对监测数据的挖掘并不够充分，有待进一步提升。

深度学习是机器学习的1个重要分支[10]，依附于大量的数据来训练模型[7]，拥有较强的自适应特征学习能力，适用于大数据背景下冲击地压监测数据的分析需求。卷积神经网络是深度学习的代表算法之一，在煤岩动力灾害方面得到了广泛的研究和应用。荀晓玉等[11]将卷积神经网络与长短时期记忆网络结合，从时间序列的角度对采煤工作面瓦斯浓度进行预测；董陇军等[12]根据微震事件和爆破事件的波形的不同特征，建立了1种基于卷积神经网络的波形辨识模型；裴艳宇等[13]建立一维卷积神经网络微震能级时序预测模型，以前若干次微震的能量级别作为输入来预测下1次微震事件的能量级别。卷积神经网络在异常信号辨识、时序数据特征提取和预测方面展现了较强的能力。

本文利用一维卷积神经网络具有对时序数据特征提取的能力，以矿山现场主要使用的微震监测为对象，建立冲击地压预警模型，能够结合专家经验挖掘定性信息，与定量信息相结合，充分获取微震监测数据的潜在特征信息，可为冲击地压监测预警提供新的尝试，也可为地音、电磁辐射等其他监测手段智能化预警提供参考。

1 一维卷积神经网络简介

一维卷积神经网络常用于序列类的数据处理，将著名的卷积运算和神经网络结合在一起，通过反向传播算法更新网络参数。如图1所示，其结构主要包括输入层、卷积层、池化层、全连接层和输出层[14-17]。

图1 典型的一维卷积神经网络结构Fig.1 Typical structure of one-dimensional convolutional neural network

卷积层类似于前馈神经网络的神经元，能对输入的数据进行特征提取[16-17]，其中包含多个卷积核，卷积核对输入的特征矢量进行卷积运算，并用非线性激活函数构建输出特征矢量[18-19]，如式(1)所示：

(1)

常用的激活函数有ReLU函数，sigmoid函数，如式(2)～(3)所示：

ReLU:f1(x)=max(0,x)

(2)

(3)

池化层能进行特征提取和信息过滤，避免模型过拟合，常用最大池化，池化层一般放置在卷积层的后面。全连接层用来实现对特征的“展平”，即将所有特征矢量首尾连接形成一维向量[19]。最终由输出层输出目标结果。

2 基于一维卷积神经网络的冲击地压预警模型

矿山微震数据是离散的一维时序数据，而一维卷积神经网络对时序数据具有较强的特征提取能力，能最大限度地提取数据特征[15-19]，本文利用微震监测数据和一维卷积神经网络来建立冲击地压预警模型，模型建立过程包括以下步骤：1)建立打分系统，制作微震监测数据标签；2)生成数据集；3)构建一维卷积神经网络模型，并将数据集输入模型中进行训练；4)完成训练，确定模型结构和参数。具体流程如图2所示。

图2 冲击地压预警模型构建流程Fig.2 Construction flow chart of rockburst early-warning model

2.1 建立打分系统

由于对矿山生产安全高度重视，矿山冲击地压事故发生次数骤减，将实际发生的冲击地压作为预警标签建立深度学习模型并不可观。为了解决深度学习训练数据缺少标签的问题，本文建立打分系统，采用专家评判方法制作微震监测数据标签，以便于生成数据集。打分系统包含微震监测数据库，该系统可随机选择历史时刻t，并展示出该时刻历史微震监测数据及其特征参数的图像，如图3(a)～图3(c)所示，分别为t时刻前n天的微震事件能量柱状图、t时刻前m天的日总能量柱状图、t时刻前m天的日频次折线图，这里取n=3，m=20。打分系统的使用步骤为：将微震监测数据导入打分系统，并首次输入历史时刻t，生成t时刻可视化图像，专家对t时刻冲击地压危险进行评判，评判完成后保存，即可自动转换为下一时刻，这里时刻t的间隔为3 h。

图3 专家打分系统中微震监测数据及其特征参数示例Fig.3 Examples of MS monitoring data and its characteristic parameters in expert scoring system

专家依据自身经验通过打分系统对某时刻t冲击地压危险进行分析评判，得到冲击地压危险评判值，即为样本标签。专家评判分值的范围是0～100，分值越高越危险，参照冲击地压危险常用的4个等级，其中，0～25为无冲击危险，25～50为弱冲击危险，50～75为中等冲击危险，75～100为强冲击危险。

2.2 建立数据集

本文以新疆某冲击地压煤矿为研究背景，煤层倾角87°～89°，是典型的急倾斜煤层，已开采+450水平B1+2和B3+6煤层，现开采+425水平B3+6煤层，采用水平分段放顶煤的采煤方法如图4所示。该矿采用ARMIS M/E微震监测系统，可对微震事件进行实时监测，自动记录微震活动，并对微震进行震源定位和能量计算，其微震探头和拾震器的布置方案随着回采面推进位置的变化而变化。

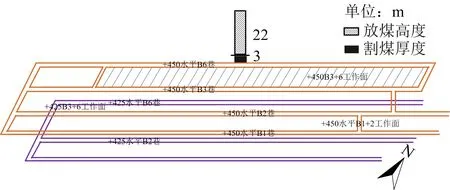
图4 新疆煤矿采掘平面Fig.4 Mining plane of a coal mine in Xinjiang

本文选用该矿+450水平B3+6工作面(2018.08—2019.07)和+425水平B3+6工作面(2019.08—2020.05)的微震数据，总采样区间为2018年8月—2020年5月，采样时刻t可由打分系统在采样区间内自动转换，时间跨度较长，能够克服样本类型单一问题。

冲击地压预警方法采用有监督学习方式，需要同时具备特征和标签信息。样本特征X为t时刻对应的微震监测数据及其特征参数，可视化后即图3(a)～图3(c)，分别为t时刻前3 d的微震事件能量柱状图、t时刻前20 d的微震日总能量柱状图、t时刻前20 d的微震日频次折线图；样本标签Y由现场冲击地压监测技术人员、防冲副总及科研院所冲击地压研究人员共计8人组成，通过打分系统对t时刻的冲击地压危险进行分析评判，获取t时刻样本标签，共生成2 360个不同时刻的样本。

根据细化的专家评判标准计算样本分布，4个等级的样本数分别为624，525，755，456，样本类别分布不平衡，为提高卷积神经网络模型的训练效果，使用SMOTE算法对少数类样本进行过采样，增加少数类样本数量。SMOTE算法在过采样时并不是简单地复制样本，而是通过K近邻插值的方法在2个少数类样本间合成新的样本，原理如图5所示，该方法可以降低模型过拟合风险[20-21]。最终生成3 000个类别平衡的样本集。如表1所示，每个样本提取出特征760个，其中，t时刻前3 d的微震事件720个(时间窗为6 min，若某个时间窗内无微震事件，则为0)，t时刻前20 d微震事件日总能量20个，t时刻前20 d微震事件日频次20个，即Xi={x1,x2,…,x760}，其中i=1,2,…,3 000，表示样本个数。将数据集中全部样本按照时间顺序进行排序，取前85%的数据作为训练集，共2 550个，后15%数据作为测试集，共450个。

图5 SMOTE算法原理Fig.5 Principle of SMOTE algorithm

表1 部分数据集Table 1 Part of data set

2.3 构建一维卷积神经网络模型

相比于传统神经网络，卷积层和池化层是卷积神经网络特有结构，卷积层中的卷积核包含权重系数和偏置，可通过反向传播算法进行更新[13]。

构建冲击地压预警的一维卷积神经网络模型，输入层是将训练集单个样本的760个特征作为输入，并对输入数据进行Z-score标准化，消除特征之间量纲及取值范围差异的影响；设置5层卷积层，每层卷积层使用数量不等的卷积核，采用等宽卷积方式；使用非限制单元(Rectified Linear Unit,ReLU)作为激活函数，增强模型的非线性表达，ReLU可解决sigmoid、tanh中常见的梯度消失问题，计算速度也最快；设置3层池化层，采用最大池化(Max Pooling)，通过池化操作降低卷积层输出的特征向量的维度，大大降低输入到全连接层的网络模型参数，降低训练难度和时间[13,22-23]；并在全连接层之前添加dropout层，系数为0.4，防止过拟合[16]；最后由输出层(回归层)，输出冲击地压危险预测值。具体模型结构如图6所示。

图6 冲击地压预警的一维卷积神经网络模型结构Fig.6 Structure of one-dimensional convolutional neural network model for rockburst early-warning

2.4 完成训练得到预警模型

本文借助Python语言运用Keras深度学习框架实现冲击地压预警模型的搭建和训练，选用Nadam优化器来训练网络，初始学习率为0.001，最大训练次数为70，小批量大小为64，L2正则化系数为0.000 1。如图7所示，用损失函数以及平均绝对误差MAE来反映模型的训练过程，平均绝对误差是性能度量的指标，损失函数为均方误差MSE，如式(4)～(5)所示：

(4)

(5)

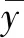
用决定系数R2评估模型的泛化能力，如式(6)所示：

(6)

用L2正则化来限制权重大小，以避免模型过拟合，如式(7)～(8)所示：

J=J(θ)+λR(ω)

(7)

(8)

式中：J(θ)为原始损失函数；λ为正则化系数；R(ω)为模型复杂度；ω为权重。

图7 冲击地压预警模型训练过程Fig.7 Training process of rockburst early-warning model

3 模型预警效果分析

3.1 测试集结果分析

基于上文搭建的一维卷积神经网络模型，用450个测试集数据进行模型测试，4个等级的样本数分别为122，103，133，92。如图8和图9分别展示训练迭代次数对测试集冲击地压危险预测结果的影响、测试集平均绝对误差的变化情况。由图8～9可知，20次迭代后，MAE迅速下降，MAE为12.5，测试集冲击地压危险的预测结果与专家评判结果拟合效果良好；迭代30次后，MAE为8.9，较迭代20次弱冲击危险、强冲击危险值拟合效果更好；之后随着迭代次数的增加，部分危险值拟合效果明显变差，且MAE无明显变化，甚至出现小幅度提升，有过拟合风险。从模型预测效果和训练速度考虑，训练次数为30时最佳，此时，冲击地压危险预测结果和专家评判结果的波动趋势基本吻合，平均绝对误差MAE最小，且83%的样本绝对值误差小于15，其中误差小于10的占80%，只有极小部分样本绝对值误差在15～20之间。由于人的主观意识的影响，误差结果在可接受范围之内。

图8 训练迭代次数对测试集冲击地压危险预测结果的影响Fig.8 Influence of training iteration times on prediction results of rockburst risk by test set

图9 训练迭代次数的增加对测试集预测结果的平均绝对误差的影响Fig.9 Influence of increase of training iteration times on MAE of prediction results by test set

运用平均绝对误差MAE、均方根误差RMSE、决定系数R2对模型性能进行评估[24]，如表2所示，3个评估指标在训练集的结果比测试集稍好，但二者相差极小，这是符合实际的，说明并未出现过拟合；且测试集决定系数R2为0.78，说明模型的可解释性强，泛化性能较好。

表2 模型性能评估Table 2 Model performance evaluation

3.2 现场应用验证

选取该矿2020年8月1日—2020年9月18日的微震监测数据进行现场验证，因矿井没有发生冲击地压，而大能量矿震与冲击地压的发生密切相关[22,25]，故将大能量矿震作为预警目标，以该矿历年矿震事件为参考，结合矿井生产实际，将大能量矿震定义为震动能量大于105的微震事件。将本模型的预警结果由0～100映射到0～1，与该矿井实际使用的算法模型的预警结果进行对比，如图10所示。

图10 本文模型与矿井原有模型预警结果对比Fig.10 Comparison of early-warning results between this model and original model of mine

由图10可知，在研究时段内共发生5次大能量矿震事件，在每次大能量矿震发生前5 d内，本文模型均进行冲击地压危险预警，预警中等冲击危险等级4次、弱冲击危险等级1次；而矿井原有使用的预警模型预警了4次，预警中等冲击危险等级2次，弱冲击危险等级2次，有1次没有给出预警。可见，本文提出的预警模型准确度更高，具有一定的实际意义。

同时，由图10可知，本文模型预警结果整体上较矿井原有模型预警结果的危险程度更高，且本文模型可以较好对专家打分进行预测，这也说明，本文模型现场应用时预警结果整体偏高与专家打分较高有关，下一步需增加打分专家的人数和样本集的数量，对模型进行进一步训练和完善。