寻找“丢失的一角”
2022-11-11方芳
方芳
[摘 要]小学生的数学学习应当是一个完整的过程,因为只有“完整地学”才能培养完整的人。文章指出数学学习中“丢失的一角”的现状,利用情境串联式微课、一点突破式微课、自定义式微课、专题探究式微课等补偿式微课,不断完善学生的知识体系,促进学生全面发展。
[关键词]补偿式微课;小学数学;完整发展
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2022)23-0004-03
儿童的全面成长需要完整的教育视域,与之相悖的是,数学学习过程的残缺与零碎会导致儿童丢失了完整学习中的某一角,比如学习兴趣、知识的形成过程、自主选择的空间、学科育人的关怀等。数学补偿式微课这种新型的学习载体能够帮助学生在形式多样的微课中找回“丢失的一角”,让学生的学习过程更完整,使学生获得数学素养的全面提升。
一、审视:数学学习中“丢失的一角”
1.丢失主动学习的兴趣
随着新课改的不断推进,数学课堂的样态发生了良性的变化,但也出现了不合时宜的情形:为了更高效地教学,直击数学知识本质,一些教师选择在教学中“去情境化”,舍弃情境创设、儿童表达和生活欣赏等过程,让数学学习失去了趣味;或是保留了部分情境,但只是为情境而情境,随意展示情境后就置之不理;或是情景画面枯燥,色彩單调,根本无法激发学生的学习兴趣。
2.丢失知识形成的过程
数学学习中重结果、轻过程的现象屡见不鲜,导致学生无法在课堂上完整地经历一些必要的数学学习过程,如尝试、体验、推导、想象等,很多数学概念、公式的习得都是直接记忆。如果教师的结构意识淡薄,学生进行结构化统整的时间和机会就会少之又少,而缺乏知识结构化的学习过程必然不是完整的。
3.丢失自主选择的空间
常听到课堂上有教师说:“大多数人已经做好了,我们一起来看一看。”“你的想法很独特,课后我们再交流。”“你还有其他方法?因为时间关系,下节课我们再交流。”……这些话其实都是礼貌性的拒绝,看似民主自由,实则学生还是被教师那根“绳”牵着走。
4.丢失学科育人的关怀
学生想要成长为一个全面发展的人需要许多品质,这就需要教师给予学科育人的关怀。有的教师虽然在教学目标中标明情感、态度与价值观教育的目标,但教学实施过程中则一味地追求效率,忽视了这些目标的落实。还有一些教师没有利用讨论、探究等教育方式,只在课始或课尾展示一句数学家名言或是一段数学历史小故事,这种浅层次的“照拂”恰恰反映了教师对数学育人方面的关注不足、行动不够。
二、实践:在补偿式微课中寻找“丢失的一角”
在信息化的时代背景下,补偿式微课可以打破课堂教学时间和空间的限制,它灵活多变的特点恰好契合不同儿童的不同需求。每个儿童“丢失的一角”各不相同,数学补偿式微课能为儿童的完整学习打开另一扇大门。
1.情境串联式微课,激发学习兴趣
兴趣是最好的老师,学习兴趣对数学这门极具抽象性特点的学科来说尤为重要。数学微课情境丰富、互动性强,能促使学生投入足够的注意力和发挥主观能动性,有效激发学生的学习兴趣。
(1)趣从“美”中来
微课的情境创设力求图、文、声、像完美结合,形成整体的美感。如“轴对称图形”一课,为了让学生更好地领悟对称的美,可设计这样的微课:伴随着悠扬的乐曲,自然景观中的轴对称现象映入眼帘……画面一转,极具中国特色的传统建筑宏伟壮丽……抬头望去,飞机在空中翱翔,蝴蝶翩翩起舞……从柔和宜人的自然之美,到令人自豪的建筑之美,再到让人赞叹的功能之美,层层深入,抓人眼球,学生沉浸其中,领悟对称的美、数学的美也就水到渠成了。
(2)趣从“爱”中来
微课的情境要具有游戏感和故事性。如教学了乘法口诀和乘加、乘减之后,可设计“糕宝拜师学做糕点” 微课。层层递进的问题和连贯的故事让学生产生浓厚的兴趣,学生能在连续的闯关过程中掌握算法、理解规律。微课里也可以加入学生喜爱的元素,如在“9的乘法口诀”的微课中就用动画演示了“螺丝钉”中的“手指操”。充满学生喜爱元素的情境串联式微课,不但能使学生认真观察与倾听,而且学生还会模仿与记忆。
2.一点突破式微课,促进深度理解
(1)动态展示,突破有限,走向极限
学生在经历知识的形成过程中经常需要想办法验证自己的猜想,但由于认知和动手能力有限,动手操作误差较大。因此,教师可以借助微课将复杂的极限情况完整地展示出来。
比如,“圆的面积”一课,割圆术和将圆转化成近似长方形这两种面积推导方法都蕴含转化和极限思想。然而在实际探究过程中,学生能够等分圆的边数和份数是有限的,操作难度也很大。借助微课的动态演示则能直观、完整、严谨地呈现割圆术的探究过程。随着割圆次数的慢慢增加,学生逐渐感受到极限思想。对于将圆转化成近似长方形的方法,学生往往会有这样的疑问:明明拼出来的是平行四边形,为什么一定要说是转化成近似长方形呢?此时,借助微课可以推动学生进行更深层次的探索:先逐步呈现8等分、16等分……到近似无穷等分的过程,再通过观察、比较引导学生进一步思考“当作平行四边形能不能推导?”“将圆极限地看作长方形有什么优势?”“圆的面积和转化后图形的面积之间到底有什么样的关系?”……
现今的课堂教学正在从“以教为中心”转向“以学为中心”,需要让学生经历完整的知识形成过程,让学生想清楚、说明白、悟得透。微课就能对学生的表达和操作进行补充,引导学生深度探究与感悟。
(2)活动支撑,突破浅表,抵达本质
抵达数学知识的本质是小学数学教学的核心。在微课中设计充分的活动,就能助力学生深度理解数学知识的本质。如“长方体的认识”这一课的教学重难点是理解棱的概念,微课就安排了两次活动,引导学生观察、想象、操作、推理,使得长方体的本质特征在学生的头脑中逐渐变得清晰。
第一个活动:聚焦观察。课堂时间有限,聚焦观察的活动能引领学生深度观察。看、摸、量等都是观察,充分观察有利于学生深入、主动地探究长方体的本质特征。最后通过问题“你观察的长方体都是这样的形状吗?有没有特殊的?”引导学生在对比和纠错中理解长方体的本质特征。
第二个活动:聚焦操作。“抽抽乐”活动:用12 根小棒和8个顶点搭建一个长方体,并思考“抽掉哪些小棒后还能想象出长方体原来的样子?最少要保留几根?”在充分思考和动手操作中,学生对长方体的特征有了进一步的理解,明确了“长方体的长、宽、高决定了长方体的形状”这一数学本质,积累了丰富的活动经验。
(3)知识勾连,突破零散,走向结构
整理与建构是数学学习过程中不可缺失的一环。微课能把知识连成片、穿成串,再建构知识网:一是引导学生进行知识的对比与发现;二是呈现多样态的、完整的知识网,让学生学会结构化地学习。
比如,对于“多边形的内(外)角和”,可设计三角形的内角和、多边形的内角和以及多边形的外角和三个微课。这三个微课都聚焦验证多边形的内角和及外角和的多种方法,通过形象生动的动画演示和讲解,沟通多种验证方法之间的联系,探究公式“180°×(边数-2)”中为什么要减2,让学生理解多边形内角和及外角和的本质含义。这样的微课层次清楚、由淺入深,利于学生形成一个清晰完整的知识结构与脉络。
3.自定义式微课,打开学习方式
作为教师,首先要看得见学生知识水平之间的差异;其次得看得到学生的困惑,了解学生的水平及他们的需求;最后还要看得远,设计不同发展目标的分层次任务,给予学生选择的机会。
(1)自选内容,发展个性
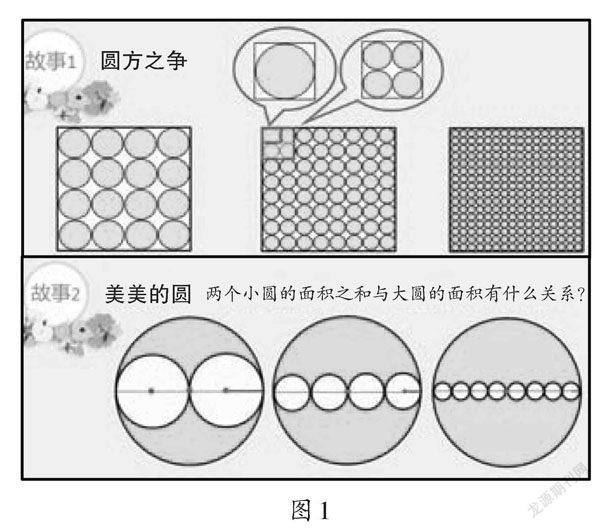
比如,对于“圆的面积”,教师可设计三个微课供学生选择:第一个是圆的面积公式推导过程的详解,对推导过程理解不到位的学生可通过这个微课巩固新知;第二个是圆的面积公式的应用的拓展练习,帮助中等水平学生提升思维能力;第三个是深度练习微课(如图1),通过探索正方形与圆、大圆与小圆之间的关系与规律,给高水平学生搭建展现数学思维能力的舞台。
(2)自选伙伴,提升素养
利用微课进行个性化学习时,学有余力的学生可以自主开发和制作微课,真正成为学习活动的主体。学生可以独立完成,也可以选择学习伙伴组成学习小组。一起完成选题、研究、录制等过程能锻炼学生的自主学习能力,学生能够从中体验成功的快乐,为终身学习奠定基础,而“教是为了不教”的目标也得以实现。
4.专题探究式微课,延展学习边界
不同专题的探究式微课可以延展数学学习的边界,为学生打开更多的“窗”。数学文化、数学实验等都能成为学生的学习素材,不同的专题探究能助力学生发展成为更完整的人。
(1)文化浸润类
数学本身就是一种文化,数学文化类微课能让学生慢慢地“感”和“悟”数学的价值。 澳大利亚学者Gail Fitz Simons和Wee Tiong Seah指出:“在数学课堂中进行价值观教育对学生个人和社会身份的获得起着非常重要的作用,这种价值观教育应该在数学课堂中处于优先地位,因为它们能够对学生是否关注或喜欢数学产生深远的影响。”
比如,教学“认识方程”之后,教师可安排学生观看《中外历史上的方程求解》微课,从方程的出现,到埃及底比斯的《莱因德纸草书》,再到《九章算术》《几何原本》《缉古算经》,以及“立成释锁法”“增乘开方法”“正负开方术”……在漫长的方程发展历史中,学生看到数学知识不断更迭发展,体会到数学家严谨的研究态度和孜孜不倦的探索精神,这些情感、态度与精神是学生数学学习的“远方”。
(2)实验探究类
让学生积累数学活动经验,培养学生的应用意识和创新意识是数学课程的重要目标。数学实验是实现这些目标的一个有效载体,而微课能解决数学实验时间和空间限制的问题。
比如,“巧算土豆的体积”微课中就能演示多种测量不规则物体体积的操作方法:将土豆的体积转化成土豆浸没后上升的水的体积,或是通过重量和体积之间的正比例关系求出土豆的体积,还可以将蒸熟的土豆重新塑形等。充分、完整的实验过程能帮助学生深入理解体积的含义,领会其中蕴含的数学思想方法和科学精神。
再如,“大树有多高”微课就是通过两个操作活动启发学生思考:不同时间测量3根同样长的竹竿的影长,体会太阳照射角度不同,影子的长度也不相同;测量3根不同长度的竹竿的影长,发现在同一地点、同一时间的前提下,物体的高度和影长成正比例关系。在微课的指导下,学生动脑、动手,积累了基本的数学活动经验。两次实验看似独立,但解决问题的方法却有共性。比较两次实验,能够帮助学生建立正比例应用的模型,启发学生的思维,让学生的数学学习浑然天成。
(3)难点突破类
学生学习过程中遇到的困难有很多,解决这些困难的过程也是学生思维能力提升的过程。难点突破类微课主要围绕一个学习难点,以解决2~3个典型问题,再进行方法比较和总结提升。
比如,“糖水中的变与不变”微课就是围绕浓度问题分加溶剂、加溶质、加溶液三种情况精选例题,引导学生明确解决问题时需要分析哪个量是变的,哪个量是不变的,进而归纳出只要抓住“不变的量”就能巧妙解决问题,使学生感悟到“变与不变”的辩证思想,突破认知难点,提升思维能力。
小学数学补偿式微课能为小学数学教育打开一扇窗,学生从中能寻找到“丢失的一角”,并努力勾画数学学习之“圆”、生命成长之“圆”。
[ 参 考 文 献 ]
[1] 丁爱平.“完整地学”:小学数学学科育人的生动实践[J].教育视界,2019(24):42-45.
[2] 吴文娟.小学数学拓展性微课课程的开发与应用研究[J].江苏教育研究,2018(31):48-51.
